Лабораторна робота № 10

ПЕРЕХІДНІ ПРОЦЕСИ В КОЛИВАЛЬНОМУ КОНТУРІ ПРИ ДІЇ ГАРМОНІЧНОЇ НАПРУГИ

Мета роботи – дослідження впливу параметрів кола і джерела на характер перехідних процесів.

Опис роботи

В роботі досліджуються перехідні процеси в колі, схема заміщення якого наведена на рис. 30.

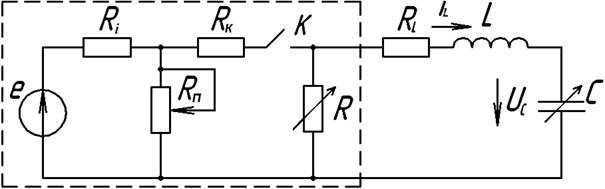
Рисунок 30 – Розгалужене електричне коло другого порядку

На рис. 30 e і – параметри генератора (е. р. с. і внутрішній опір); К – електронний ключ, який комутується з частотою 50 Гц, а – його внутрішній опір в замкнутому стані; R i C – змінні опір і ємність з блоків БЗО і БЗЄ; L і – параметри котушки індуктивності (елемент набірного поля УДЛС); – потенціометр на 100 Ом. Опір ключа в розімкнутому стані вважається нескінченно великим.

Перехідний процес в колі рис. 30 виникає як при замиканні, так і розмиканні ключа (switch). Після розмикання ключа спостерігається вільний перехідний процес. Якщо опір R взяти достатньо великим, то цей процес, на мить замикання ключа, встигне згаснути і в колі будуть мати місце нульові початкові умови. Прийнявши мить замикання ключа за початок відліку часу можемо записати і .

Після замикання ключа в колі будуть спостерігатись як вимушені, так і вільні коливання (free oscillation), аналіз яких зручно провести, перетворивши обведену на рис. 30 ділянку за теоремою про еквівалентне джерело. Внаслідок отримаємо схему (рис. 31), де еквівалентні е.р.с та опір

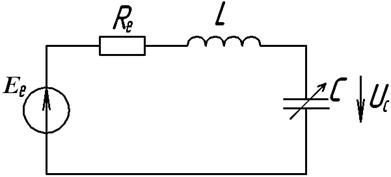
Рисунок 31 – Еквівалентна ділянка схеми за теоремою про еквівалентне джерело

При достатньо малому опорі перехідний процес в колі рис. 31 буде коливальним і напруга ємності визначиться

               (71)

де – частота вимушених коливань (forced oscillation);

і – коефіцієнт згасання (damping coefficient) і частота вільних коливань;

А і – постійні інтегрування, які визначаються з початкових умов

                    (72)

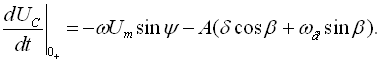          (73)

Далі обмежимося розглядом випадку, коли вільні коливання згасають повільно , а частота джерела живлення близька до частоти вільних коливань . Тоді з початкових умов знаходимо , і напруга ємності визначиться

          (74)

Якщо частоти джерела живлення і вільних коливань не просто близькі, а збігаються (), тоді виникають релаксаційні коливання (relaxation oscillation)

                    (75)

де

                    (76)

– обвідна амплітуда релаксаційних коливань. Часова діаграма релаксаційних коливань наведена на рис. 32, де пунктиром вказана обвідна амплітуд.

Рисунок 32 – Часова діаграма релаксаційних коливань

Якщо частоти вимушених і вільних коливань близькі, але не рівні () і, крім того, вільні коливання згасають настільки повільно, що за час замкнутого стану ключа можна вважати , тоді виникають коливання, які називаються биттями в колі. Нехтуючи повністю втратами енергії, тобто приймаючи отримаємо

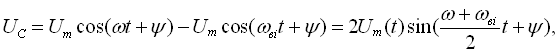     (77)

де

                    (78)

– обвідна амплітуд при биттях в колі.

На рис. 33 наведена часова діаграма напруги ємності при виниканні биття (beat) в колі без втрат енергії, де пунктиром вказана обвідна амплітуд биття.

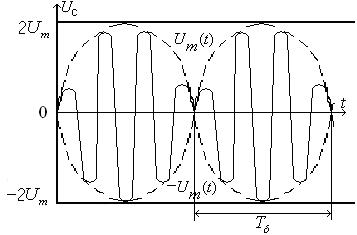
Рисунок 33 – Часова діаграма напруги ємності при виниканні биття в колі без втрат енергії

Час, через який обвідна амплітуда повторюється, називають періодом биття

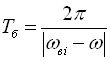.                         (79)

Биття в колі є результатом накладання вимушених і вільних коливань з близькими, але не рівними частотами. Через нерівність частот модуль різниці фаз між вимушеними і вільними коливаннями зростає з часом і, коли ця різниця стає кратною ( – період функції косинус), коливання повторюються

де – проміжки часу через який коливання повторюються. Мінімальний з цих проміжків визначає період биття ().

За аналогією зі стоячими хвилями (standing wave), точки, в яких обвідна амплітуда максимальна, можна назвати пучностями биття, а точки, де обвідна амплітуда набуває нульових значень – вузлами биття. Положення пучностей і вузлів визначається з виразу

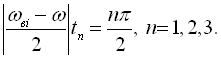               (80)

Непарним значенням n відповідають пучності, парним – вузли.

У реальних кіл вільні коливання згасають у часі, а вимушені – ні. Ця обставина суттєво ускладнює картину биття, зображену на рис. 33. Зокрема обвідна амплітуда також згасає в часі. Внаслідок, в пучностях амплітуда коливань не подвоюється, а у вузлах не набуває нульових значень.

Завдання

1. Підключити до виходу генератора частотомір, осцилограф і послідовно з’єднані електронний ключ (ЕК) і потенціометр на 100 Ом. Далі включити ЕК і змінюючи напругу і частоту генератора, а також опір потенціометра, отримати на екрані осцилографа стійке зображення у вигляді прямуючих одне за одним “гармонічних” коливань однакової частоти, але з різними амплітудами і (). Бажано, щоб менша з амплітуд відрізнялась від більшої в разів (оптимальний варіант 2 рази). Зарисувати отримані зображення і записати масштаб на осях осцилографа. Виміряти і записати частоту генератора.

2. Мостом змінного струму виміряти опір потенціометра в досліді п.1 і записати його значення.

3. Скласти коло за схемою рис. 30 і підключити до виходу генератора канал 1 осцилографа, а до ємності – канал 2. Далі зміною частоти і амплітуди напруги генератора(в гармонічному режимі роботи), а також зміною опорів , R і ємності С отримати на екрані осцилографа релаксаційні коливання (див рис. 32). Після отримання стійкого зображення, зарисувати осцилограму і записати масштаби на осях осцилографа. Частотоміром виміряти і записати частоту генератора.

Примітка. Канал осцилографа підключений до виходу генератора використати для синхронізації. В разі відсутності синхронізації перейти на інші варіанти, включно зовнішню синхронізацію.

4. Виміряти і записати використані в досліді п. 3 значення опорів , R, ємності С і параметри котушки індуктивності .

5. Змінивши незначно частоту генератора порівняно з дослідом п. 3 отримати на екрані осцилографа биття (див рис. 33) і зарисувати отриману осцилограму. Частотоміром виміряти частоту проведення досліду і записати її значення.

6. Відключити від досліджуваного в п. 3 і п. 5 кола ЕК і, закоротивши місце його ввімкнення, зміною частоти генератора отримати максимальну амплітуду коливань на ємності. Далі за осцилографом визначити амплітуду напруги на виході генератора і на ємності та записати їх значення.

Обробка результатів

1. За результатами дослідів п. 1 і п. 2 визначити внутрішній опір ЕК на підставі виразу

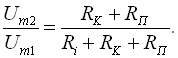
Внутрішній опір генератора взяти рівним 50 Ом.

2. За осцилограмами досліду п. 3 визначити коефіцієнт згасання і частоту вільних коливань. Порівняти частоту вільних коливань, визначену з осцилограм, і виміряну частотоміром.

3. За осцилограмами досліду п. 4 визначити період і частоту биття.

4. За результатами вимірів частоти в дослідах п. 3 і п. 5 визначити частоту биття і порівняти її зі знайденою в попередньому пункті.

5. За результатами досліду п. 3 визначити логарифмічний декремент згасання , а за ним добротність контуру

Розрахувавши також добротність за результатами досліду п. 6 порівняти її з добротністю, визначеною за логарифмічним декрементом згасання.

6. Визначити коефіцієнт згасання і частоту вільних коливань за виміряними параметрами схеми рис. 30 (див. дослід п. 4)

Контрольні запитання

1. Пояснити призначення змінних опорів і R в схемі на рис. 30.

2. Чи впливає внутрішній опір генератора (рис. 30) на згасання вільних коливань?

3. Пояснити як отримана формула, наведена в п. 1 обробки результатів.

4. Чому при рівних частотах генератора і вільних коливань биття в контурі не виникають?

5. Як за осцилограмою релаксаційних коливань визначити коефіцієнт згасання і частоту вільних коливань? Пояснити зміст цих понять.

6. Чому експериментальні часові діаграми биття в контурі відрізняються від наведених на рис. 33?

7. Пояснити зміст понять частота биття і період биття? Як ці величини визначити за відомими частотою генератора і частотою вільних коливань?

8. Пояснити зміст понять добротність контуру і логарифмічний декремент згасання. Як ці величини визначити за результатами експерименту?

9. Як за відомими параметрами елементів схеми визначити коефіцієнт згасання і частоту вільних коливань?

10. Як отримати формулу наведену в п. 5 обробки результатів?

Література

[10, С. 313–326; 11, С. 287–294; 15, С. 305–310].