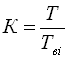Лабораторна робота № 15

ДОСЛІДЖЕННЯ ВІЛЬНИХ КОЛИВАНЬ У ПОСЛІДОВНОМУ КОЛИВАЛЬНОМУ КОНТУРІ

Мета роботи – з’ясування зв’язку між вільними і резонансними коливаннями, визначення параметрів контуру за осцилограмами вільних коливань.

Опис роботи

В роботі досліджується послідовний коливальний контур, складений з елементів набірного поля УДЛС-1, схема заміщення якого наведена на рис. 40, а.

а)                                   б)

Рисунок 40 – Послідовний коливальний контур (а) і еквівалентна схема контуру (б)

На рис. 40 прийняті такі позначення: – е. р. с. і внутрішній опір генератора; – опір і індуктивність котушки; – ємність конденсатора (конденсатор вважається ідеальним); – шунт на 5–10 Ом (усуває вплив контуру на вихідну напругу генератора); – потенціометр на 100 Ом (регулює згасання вільних коливань).

На рис. 40, б наведена еквівалентна схема контуру, в якій

, .      (136)

При проведені досліджень генератор працює в режимі “меандр”, в якому е. р. с. генератора змінюється в часі за законом, зображеним на
рис. 41.

Рисунок 41 – Часова діаграма е. р. с. генератора типу “меандр”

За аналогічним законом змінюється еквівалентна е. р. с. в схемі
рис. 40, , але максимальне її значення Далі всюди, під е. р. с. в схемі рис. 40, б буде розумітися е. р. с. зображена на
рис. 41.

1 Вільні коливання

В моменти часу (n = 1, 2, 3, …) е. р. с. в схемі рис. 40, б стрибком змінюється на , що викликає в контурі перехідний процес, який переривається наступним стрибком.

При малих втратах енергії в контурі (малий опір ) корені характеристичного рівняння будуть комплексними , а перехідний процес коливальним. Якщо період е. р. с. кратний періоду вільних коливань , то напруга ємності протягом періоду визначиться наближеним виразом

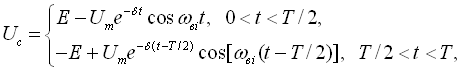          (137)

де перші доданки визначають примусові складові, а другі – вільні коливання.

Частота вільних коливань

                    (138)

при великій добротності контуру , близька до резонансної частоти , а їх амплітуда згасає в часі за експоненціальним законом

,                          (139)

де – коефіцієнт згасання. Початкова амплітуда вільних коливань залежить від співвідношення між періодами е. р. с. T і вільних коливань і визначається виразом

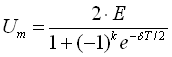                    (140)

за умови – ціле число.

Якщо період е. р. с. достатньо великий, то вільні коливання, викликані попереднім стрибком, встигають згаснути до настання наступного. В цьому випадку в останньому виразі можна прийняти . Тоді , тобто амплітуда вільних коливань не перевищує стрибків напруги на вході контуру.

Якщо Т мале, то розклавши експоненту в ряд Тейлора в околі нуля і обмежившись лінійними членами, будемо мати

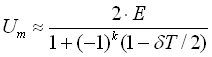.                     (141)

Враховуючи, що отримаємо

.                     (142)

Для непарних (odd) k = 1, 3, 5, …

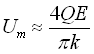,                               (143)

а для парних (even) k = 2, 4, 6, …

.                         (144)

Для непарних k амплітуда вільних коливань зростає зі збільшенням добротності (зменшенням коефіцієнта згасання), а для парних навпаки зменшується.

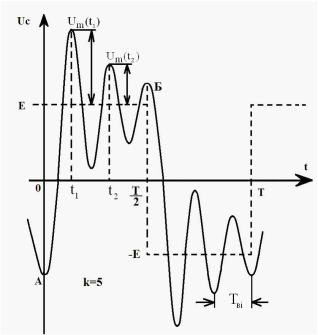
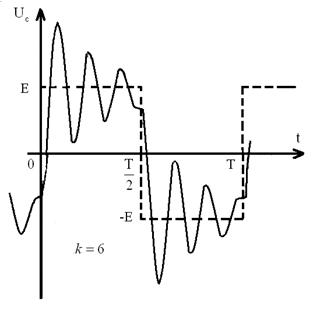
На рис. 42 наведені якісні часові діаграми напруги ємності для k = 5 (рис. 42, а) і k = 6 (рис. 42, б), які пояснюють відзначену вище залежність амплітуди від добротності для непарних і парних k (пунктиром вказана часова діаграма е. р. с. ).

Рисунок 42 – Часові діаграми напруги на ємності

Для k=5 (і інших непарних значень k ) зростання е. р. с. від –Е до +Е (або її зменшення від +Е до –Е ) відбувається в моменти часу, коли напруга ємності також починає зростати (або навпаки зменшуватись) (див. точки А і В на рис. 42, а. Тому черговий стрибок е. р. с. при непарних k підштовхує коливання, викликані попередніми стрибками, і їх амплітуда зростає.

Для k=6 (і інших парних значень k) черговий стрибок е. р. с. протидіє вільним коливанням, викликаним попередніми стрибками. Тому старі коливання гальмуються і виникають нові, амплітуда яких менша ніж при непарних k (амплітуда вільних коливань на рис. 42, б штучно збільшена).

2 Резонансні коливання

Важливий практичний інтерес має випадок, коли , а k=1. На рис. 43 наведені часові діаграми е. р. с., її першої гармоніки і напруги ємності для цього випадку (амплітуда напруги ємності штучно зменшена).

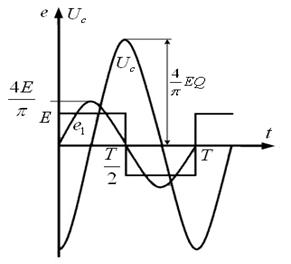
Рисунок 43 – Часові діаграми е. р. с., її першої гармоніки і напруги ємності для цього випадку

При k = 1 вільні коливання, викликані попередніми стрибками, не встигають помітно згаснути до наступного стрибка, який їх додатково підштовхує. Внаслідок цього коливання наростають доки втрати енергії в контурі і енергетична підкачка коливань джерелом не врівноважаться.

Режим роботи контуру при k = 1 називають резонансом на першій гармоніці е. р. с. Дійсно, частота першої гармоніки е. р. с. при
(k = 1) збігається з частотою вільних коливань, яка при малих втратах енергії (велика добротність Q), близька до резонансної частоти , а амплітуда першої гармоніки е. р. с. . Амплітуда першої гармоніки напруги ємності на частоті резонансу в Q разів більша , що збігається з амплітудою вільних коливань при k = 1. Звідси випливає, що резонансне збільшення напруги ємності є наслідком розкачування вільних коливань джерелом е. р. с.

Вихідна напруга високодобротного контуру в резонансному режимі практично гармонічна, а її частота збігається з частотою тієї гармоніки е. р. с. на якій має місце резонанс.

3 Визначення параметрів

Осцилографування вільних коливань (див. рис. 42) дозволяє визначити корені характеристичного рівняння контуру, а за ними – резонансну частоту і добротність.

З рис. 42 безпосередньо знаходиться період вільних коливань, а за ним і частота вільних коливань .

Дійсну частину комплексних коренів можна знайти, визначивши амплітуду вільних коливань в два різних моменти часу і ( див. рис. 42).

                         (145)

                         (146)

Прологарифмувавши відношення амплітуд, отримаємо

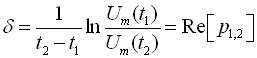.                (147)

Частота резонансу і добротність Q знаходяться з виразів

,                     (148)

.                         (149)

Резонансної частоти і добротності недостатньо для визначення еквівалентних параметрів контуру R, L, C ( див. рис. 40, б). Якщо ж прийняти, що вся індуктивність контуру зосереджена в котушці і виміряти її ( індуктивність L), то опір і ємність визначаються за виразами

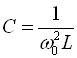,                          (150)

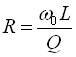.                          (151)

Завдання

1. З елементів набірного поля скласти коло за схемою рис. 40, а. До виходу генератора підключити вольтметр і канал 1 осцилографа, а до ємності також вольтметр і другий канал осцилографа.

2. В гармонічному режимі роботи генератора настроїти контур в резонанс за максимумом напруги ємності і підібрати опір потенціометра так, щоб добротність контуру становила декілька десятків одиниць. Занести покази вольтметрів і частоту генератора до табл. 38 (гармонічний режим)

Таблиця 38 – Параметри гармонічного режиму і “меандр”

3. Не змінюючи частоту і напругу генератора переключити генератор в режим “меандр”. Далі незначною зміною частоти генератора добитись максимуму напруги ємності і, настроївши осцилограф, переконатись, що максимум і мінімум напруги ємності відповідають стрибкам е. р. с. генератора. Зарисувати осцилограми вихідної напруги генератора і напруги ємності і занести покази вольтметрів до табл. 38 (режим “меандр”).

4. Зменшити частоту генератора в декілька десятків разів і настроїти осцилограф так, щоб на екрані спостерігався приблизно один період е. р. с. генератора. Потім незначною зміною напруги генератора домогтися максимального розмаху вільних коливань на екрані осцилографа. Переконатись, що при цьому має випадок рис. 42, а і зарисувати осцилограми е. р. с. генератора і напруги ємності.

5. Далі незначною зміною частоти генератора домогтися мінімального розмаху вільних коливань, переконатись, що цьому випадку відповідає рис. 42,б і також зарисувати осцилограми е. р. с. генератора і напруги ємності.

Примітка. Для обох дослідів п. 4 і п. 5 безпосередньо з екрана осцилографа визначити амплітуду і (див. рис. 42), взявши як і моменти часу, які відповідають найбільш віддаленим екстремумам на півперіоді е. р. с. Визначити також з екрана осцилографа період е. р. с. Т і період вільних коливань . Результати занести до табл. 39.

6. Мостом змінного струму виміряти індуктивність котушки і записати її значення.

Таблиця 39 – Параметри вільних коливань

Обробка результатів

1. За даними табл. 38 розрухувати добротності контуру для обох режимів роботи і результати занести до табл. 38.

Примітка. Для режиму «меандр» при розрахунку добротності діюче значення напруги на вході контуру (діюче значення першої гармоніки е. р. с. ) взяти рівним .

2. За даними табл. 39 для парних і непарних К розрахувати коефіцієнти згасання , і кутові частоти , вільних коливань. Порівняти отримані значення і занести їх до табл. 39 (величини і занести до другого рядка табл. 39).

3. За знайденими в попередньому пункті значеннями коефіцієнта згасання і частоти вільних коливань визначити частоту резонансу і добротність контуру і порівняти їх з даними табл. 38.

4. За відомими індуктивністю, частотою резонансу і добротністю визначити еквівалентні опір і ємність контуру.

5. Зробити висновки по роботі.

Контрольні запитання

1. Чому при дії на контур е. р. с. типу «меандр» в контурі виникають перехідні процеси, хоча на контур діє періодична е. р. с. ?

2. Які функції в колі рис. 40, а покладаються на опір , який шунтує контур?

3.  За яких причин амплітуда вільних коливань в контурі більша для непарних ніж для парних?

4. При якому співвідношенні між еквівалентними параметрами контуру (див. рис. 40, б) в контурі виникають вільні коливання?

5. Як згасання коливань впливає на частоту резонансу і вільних коливань послідовного коливального контуру рис. 40, б?

6. Як за осцилограмами вільних коливань визначити корені характеристичного рівняння контуру?

7. Який фізичний зміст модуля комплексного кореня характеристичного рівняння контуру, а також відношення модуля до модуля його подвоєної дійсної частини?

8. За скільки періодів вільних коливань їх амплітуда зменшиться в разів?

9. Чи будуть змінюватись частоти резонансу і вільних коливань в контурі рис. 40, а при зміні опору потенціометра ?

10.  Чому при зменшенні відношення періоду е. р. с. типу «меандр» і періоду вільних коливань () амплітуда вільних коливань зростає для непарних і зменшується для парних?

11.  Як і чому буде змінюватись амплітуда вільних коливань при відношенні () меншим одиниці?

Література

[10, С. 312–321; 11, С. 287–291; 14, С. 276–278].