3.4 Білий шум

Для аналізу радіотехнічних кіл та сигналів велику практичну цінність має специфічний випадковий процес, який теоретично має рівномірний спектр потужності по усій смузі частот:

Такий ідеалізований випадковий процес був названий білим шумом за аналогією з білим світлом, яке у видимій частині має практично рівномірний суцільний спектр.

Визначимо функцію кореляції білого шуму:

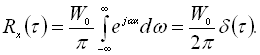
Функція кореляції дорівнює нулю усюди, крім , де вона нескінченна. Отож, миттєві значення напруги (чи потужності) білого шуму в будь-які два як завгодно близькі моменти часу некорельовані, і тому інтервал кореляції . Тому білий шум часто називають дельта Т-корельованим.

Проведемо аналітичне тлумачення поняття «білого шуму». Якщо за рівністю Парсеваля визначити його дисперсію, то отримаємо значення , що є абсурдним з фізичної точки зору. Цей результат є наслідком абстрактного уявлення про нескінченність протяжності спектра потужності по осі частот. Однак використання поняття «білого шуму» дуже зручне для аналізу характеристик випадкового процесу на виході радіотехнічних пристроїв, коли смуга пропускання радіотехнічного кола порівнянна з шириною спектра реального шуму.

При обробці в приймачі оптимальним фільтром ширина спектра білого шуму обмежується. Як наслідок шум на виході оптимального фільтра стає уже корельованим (рис. 3.18).

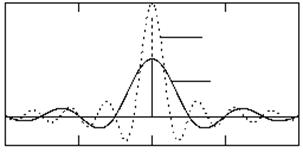
Рисунок 3.18 – Функції кореляції білого шуму

Середня потужність (дисперсія) білого шуму безмежно велика. Часова реалізація  білого шуму має голчату структуру з нескінченно тонкими сплесками обох знаків. Зазвичай розглядають білий шум, якщо ширина частот завади перевищує смугу частот пропускання апаратури, а  амплітуди частот приблизно сталі. До таких завад відносять флуктуаційні шуми, завади в багатоканальних системах зв’язку.

     3.5 Проходження випадкових сигналів через ЕС

Ефективна ширина спектра випадкового сигналу визначається як

де – максимальне значення функції і безпосередньо випливає з аналізу випадкових процесів.

Зауважимо, що ширина спектра є практичною характеристикою випадкового процесу і обчислюється, як правило, для реальних частот за одностороннім спектром процесу.

Нехай на вхід чотириполюсника (рис. 3.19) (ЕС) з передатною функцією і імпульсною характеристикою діє випадковий процес із заданими статичними характеристиками. Необхідно знайти його статичні характеристики на виході чотириполюсника.

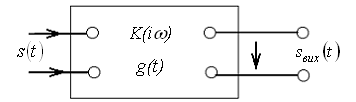
Рисунок 3.19 – Лінійний чотириполюсник з постійними параметрами

Як вже зазначалось, основними характеристиками випадкового процесу є: розподіл ймовірностей, кореляційна функція, спектральна густина потужності.

Визначити значення двох останніх досить просто. Значно складніше знайти закон розподілу випадкового процесу на виході лінійного кола. В загальному випадку при довільному розподілі процесу на виході досить складно знайти розподіл випадкового процесу на виході інерційного кола.

Процес спрощується лише при використанні нормального розподілу вхідного процесу, оскільки при будь-яких лінійних операціях з гаусовим процесом розподіл залишається нормальним і змінюються лише функції  та . Тому, якщо задано густину ймовірності вхідного процесу (з нульовим середнім)

то густина ймовірності на виході лінійного кола

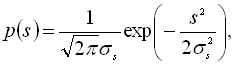
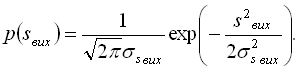Дисперсія  легко знаходиться зі спектра чи з кореляційної функції. Таким чином, аналіз передачі гаусових процесів через лінійні кола по суті зводиться до спектрального чи кореляційного аналізу.

1. У чому полягає інформаційний процес?

2. Які існують основні типи сигналів?

3. Що лежить у основі поняття спектра сигналу?

4. Для чого застосовується перетворення Фур’є?

5. Назвіть основні властивості перетворення Фур’є.

6. При виконанні яких умов є можливим подання неперіодичної функції інтегралом Фур’є?

7. Що приймають за практичну ширину спектра сигналу?

8. Для чого застосовують дискретне перетворення Фур’є?

9. Наведіть основні види модуляції сигналів.

10. Для яких сигналів і в яких випадках величини бод і біт у секунду збігаються?

11. Які види модуляції розрізняють за характером зв'язку між вхідним (модулюючим) сигналом і модульованим параметром?

12. У чому полягає ШІМ?

13. Що являє собою випадковий процес?

14. Що являє собою математичне сподівання у відношенні до сигналів?

15. Для чого призначений аналізатор закону розподілів?

16. Перелічіть основні характеристики випадкових процесів.

17. У чому сутність теореми Хінчина – Вінера?

18. Що розуміють під поняттям “білий шум”?