4.1 Цифрове подання сигналів

Під дискретизацією сигналів розуміють перетворення функцій неперервних змінних у функції дискретних змінних, по яких вихідні неперервні функції можуть бути відновлені із заданою точністю. Роль дискретних відліків виконують, як правило, квантовані значення функцій у дискретній шкалі координат.

Система дискретного часу – це алгоритм із вхідною послідовністю і вихідною послідовністю , що може бути лінійною або нелінійною, інваріантною або змінною в часі. Система дискретного часу лінійна й інваріантна в часі, якщо вона відповідає принципу суперпозиції (відгук на кілька входів дорівнює сумі відгуків на кожен вхід окремо ), а затримка вхідного сигналу викликає таку ж затримку вихідного сигналу.

Суть дискретизації аналогових сигналів полягає в тому, що неперервність у часі аналогової функції замінюється послідовністю коротких імпульсів, амплітудні значення яких визначаються за допомогою вагових функцій, або безпосередньо вибірками (відліками) миттєвих значень сигналу у моменти часу . Подання сигналу на інтервалі сукупністю дискретних значень записується у вигляді:

де – оператор дискретизації.

Запис операції відновлення сигналу :

Вибір операторів та визначається необхідною точністю відновлення сигналу. Найбільш простими є лінійні оператори. У загальному випадку:

де – система вагових функцій.

Відліки в останньому виразі пов'язані з операцією інтегрування, що забезпечує високу завадостійкість дискретизації. Однак у силу складності технічної реалізації "зваженого" інтегрування, останнє використається досить рідко, при високих рівнях перешкод. Більш широке поширення одержали методи, при яких сигнал заміняється сукупністю його миттєвих значень у моменти часу . Роль вагових функцій у цьому випадку виконують ґратчасті функції. Відрізок часу між сусідніми відліками називають кроком дискретизації. Дискретизація називається рівномірною із частотою , якщо значення постійне по всьому діапазону перетворення сигналу. При нерівномірній дискретизації значення між вибірками може змінюватися за певною програмою або залежно від зміни будь-яких параметрів сигналу.

Відтворення безперервного сигналу за вибірками може проводитися як на основі ортогональних, так і неортогональних базисних функцій. Відтворююча функція відповідно подається апроксимуючим поліномом:

де – система базисних функцій.

Оптимальними є методи дискретизації, що забезпечують мінімальний числовий ряд при заданій похибці відтворення сигналу. При неортогональних базисних функціях використаються, в основному, статичні алгебраїчні поліноми вигляду:

Якщо значення апроксимуючого полінома збігаються зі значеннями вибірок у моменти їхнього відліку, то такий поліном називають інтерполяційним. Як інтерполяційний поліноми звичайно використовуються багаточлени Лагранжа. Для реалізації інтерполяційних поліномів необхідна затримка сигналу на інтервал дискретизації, що в системах реального часу потребує певних технічних рішень. Як екстраполяційні поліноми використовують, як правило, багаточлени Тейлора.

Природною вимогою до вибору частоти дискретизації є внесення мінімальних перекручувань у динаміку зміни сигнальних функцій. Логічно думати, що перекручування інформації будуть тим менші, чим вища частота дискретизації . З іншої сторони також очевидно, що чим більше значення , тим більшою кількістю цифрових даних будуть відображатися сигнали, і тим більший час буде затрачатися на їхню обробку. В оптимальному варіанті значення частоти дискретизації сигналу повинно бути необхідним і достатнім для обробки інформаційного сигналу із заданою точністю, тобто забезпечувати припустиму похибку відновлення аналогової форми сигналу (середньоквадратичну в цілому за інтервалом сигналу, або за максимальними відхиленнями від дійсної форми в характерних інформаційних точках).

Під квантуванням (англ. quantization) розуміють перетворення безперервної за значеннями величини у величину з дискретною шкалою значень із скінченної безлічі дозволених, які називають рівнями квантування. Якщо рівні квантування нумеровані, то результатом перетворення є число, що може бути виражене в будь-якій числовій системі. Округлення з певною розрядністю миттєвих значень безперервної аналогової величини з рівномірним кроком за аргументом є найпростішим випадком дискретизації й квантування сигналів при їхньому перетворенні в цифрові сигнали.

Дискретизація аналогових сигналів з перетворенням у цифрову форму пов'язана із квантуванням сигналів. Сутність квантування полягає в заміні незліченної безлічі можливих значень функції, у загальному випадку випадкових, скінченною безліччю цифрових відліків, і виконується округленням миттєвих значень вхідної функції у моменти часу до найближчих значень , де – крок квантування шкали цифрових відліків. Квантування з постійним кроком називається рівномірним.

При квантуванні сигналів у великому динамічному діапазоні значень крок квантування може бути й нерівномірним, наприклад, логарифмічним, тобто пропорційним логарифму значень вхідного сигналу. Установлений діапазон шкали квантування від до і крок квантування визначають число розподілів шкали і відповідно цифрову розрядність квантування. У результаті дискретизації й квантування безперервна функція заміняється числовою послідовністю {}. Похибка округлення називається шумом квантування. Необхідна точність квантування оцінюється за впливом виниклого шуму квантування на наступну обробку сигналів.

При досить малому кроці квантування будь-яке значення в його межах можна вважати рівноймовірним, при цьому значення розподілені за рівномірним законом.

Вхідний сигнал містить, як правило, адитивну суміш корисного сигналу і перешкоди .

На практиці крок квантування вибирають звичайно таким, щоб не відбувалося помітної зміни відношення сигнал/шум.

Тепер перейдемо до подання сигналів у неперервній формі. Поштовхом до подання неперервних (аналогових) сигналів у цифровій формі стала необхідність засекречування мовних сигналів під час другої світової війни. Ще більшим стимулом до цифрового перетворення аналогових сигналів було створення комп'ютера, який можна використовувати як кінцевий пристрій системи передачі цифрової інформації, доручаючи йому виконання логічних операцій з прийому та обробки сигналів.

У наш час у цифровій формі можна передавати будь-який вид інформації, забезпечуючи необхідну надійність за значної швидкості передачі. Сильним поштовхом у розвитку цифрових систем передачі інформації послужило створення інформаційно-обчислювальних мереж і наявність технологічної бази для виробництва високошвидкісних перемикачів, широкосмугових модемів, мультиплексорів, підсилювачів та ін.

Кодуванням є подання за певними правилами дискретних повідомлень у деякі комбінації, складені з певного числа елементів-символів. Ці елементи називаються елементами коду, а число різноманітних елементів, із яких складаються комбінації, – основою коду. Елементи коду утворюють кодові комбінації. Наприклад, якщо ми складаємо комбінації із різноманітних сполучень (0 і 1), то це – код із основою два або двійковий код. Якщо всі комбінації мають однакове число знаків, код називається рівномірним. Широко відомий код Морзе – нерівномірний код. Правило кодування звичайно виражається кодовою таблицею, в якій кожному символу повідомлення ставиться у відповідність певна кодова комбінація.

Кодове подання дискретних значень сигналу здійснюється за допомогою цифр, але не обов'язково десяткових. Нагадаємо, що в десятковій системі, називаючи число, ми вказуємо, скільки одиниць від нуля до дев'яти є в розряді одиниць, у розряді десятків, сотень, тисяч і т. д. Те саме відбувається в будь-якій іншій системі числення з іншою основою. У десятковій системі користуємося десятьма цифрами: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. У двійковій системі числення в нашому розпорядженні тільки дві цифри: 0 та 1. Тому десяткова цифра 23, наприклад, у двійковій системі виглядатиме так:

1  2⁴ + 0 2³ + 1 2² +1 2¹ + 1 2⁰ =23,

і це число запишеться в послідовності розрядів як 10111.

На рис. 4.1. показаний процес цифрового подання інформації квантуванням за: а) частотою і б) амплітудою.

Двійкова система числення широко використовується в обчислювальній техніці та зв'язку внаслідок використання електричних і електронних приладів із двома елементами стану (реле в замкнутому або розімкнутому стані, магнітний матеріал намагнічений або розмагнічений, два можливих стани тригера). Дуже зручним з погляду створення і розпізнавання є сигнал, що має два стани: "так" або "ні" (1 або 0).

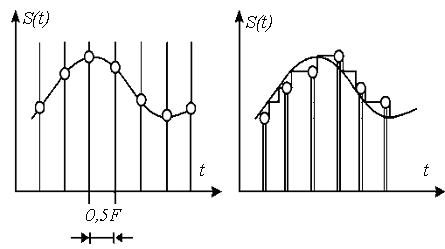
а) подання сигналу, узяте через інтервал 1/2F   б) сигнал, квантований за рівнем

Рисунок 4.1 – Подання аналогового сигналу у вигляді дискретних відліків (вибірок)

Отже, однією з головних переваг передачі інформації в цифровій формі є можливість використання кодованих сигналів і оптимального в заданих умовах способу їх прийому. Важливо, що за цифрової передачі усі типи сигналів, такі як мова, музика, телебачення, дані, можуть об'єднуватися в один загальний потік інформації, передача якого формалізована. Крім того, ущільнення при одночасному використанні комп'ютера дозволяє більш ефективно використовувати спектр і час, захистити канал від несанкціонованого доступу, об'єднати в єдиний процес передачу цифрової інформації і цифрової комутації каналів та повідомлень.

Звичайно, за деякі переваги цифрових видів передачі необхідно сплачувати, зокрема, більшою шириною спектра сигналу, що випромінюється, наявністю міжсимвольних перешкод, необхідністю синхронізації систем передачі та інше. Темпи впровадження цифрової техніки говорять про те, що всі ці труднощі можливо подолати.

А тепер розглянемо відновлення сигналів. Відновлення неперервного сигналу за вибірками може проводитися як на основі ортогональних, так і не ортогональних базисних функцій. Відновлююча функція відповідно подається апроксимуючим поліномом:

де – система базисних функцій.

Ортогональні базисні функції забезпечують збіжність ряду до при . Оптимальними є методи дискретизації, які забезпечують мінімальний числовий ряд при заданій похибці відтворення сигналу. При неортогональних базисних функціях переважно використовуються степеневі алгебраїчні поліноми вигляду:

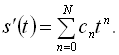
Якщо значення апроксимуючого полінома збігаються зі значеннями вибірок в моменти їх відліку, то такий поліном називають інтерполювальним. Як інтерполювальні поліноми зазвичай використовуються багаточлени Лагранжа. Для реалізації інтерполювальних поліномів необхідна затримка сигналу на інтервал дискретизації, що в системах реального часу потребує певних технічних рішень. Як екстраполювальні поліноми використовують, як правило, багаточлени Тейлора.

Зрозумілою вимогою до вибору частоти дискретизації є внесення мінімальних спотворень в динаміку змін сигнальних функцій. Логічно вважати, що спотворення інформації будуть тим менші, чим вища частота дискретизації . З другого боку, також очевидно, що чим більше значення , тим більшою кількістю цифрових даних будуть відображатися сигнали, і тим більший час буде затрачено на їх обробку. В оптимальному варіанті значення частоти дискретизації сигналу повинне бути необхідним і достатнім для обробки інформаційного сигналу з заданою точністю, тобто забезпечувати допустиму похибку відновлення аналогової форми сигналу (середньоквадратичну в цілому за інтервалом сигналу, або за максимальними відхиленнями від істинної форми в характерних інформаційних точках сигналів).

Теорема Котельникова

Частотний критерій Котельникова базується на теоремі Котельникова: якщо неперервна функція відповідає умовам Діріхле (тобто, обмежена, кусково-неперервна і має кінцеву кількість екстремумів) та її спектр обмежений деякою частотою – то вона повністю визначається послідовністю своїх значень в точках, які розташовані одна від одної на відстані

.

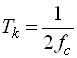Аналітично теорема Котельникова записується інтерполяційним рядом

     ,    

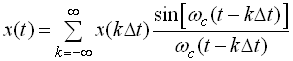де .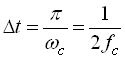

Очевидно, що неперервна функція з обмеженим спектром може бути подана у вигляді суми нескінченно великої кількості членів, кожний з яких є множником функції вигляду (функції відліку) та коефіцієнта , який визначає значення функції в момент відліку.

Функція вигляду 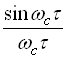являє собою реакцію ідеального фільтра нижніх частот з граничною частотою на дельта-функцію. Тоді, якщо через такий фільтр пропустити квантований в часі сигнал із частотою квантування 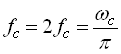, то, знаходячи добуток вихідних сигналів фільтра, можна отримати вихідний неперервний сигнал функції .

При використанні теореми Котельникова для квантування сигналів реальний спектр сигналу умовно обмежують деяким діапазоном частот від нуля до , в якому зосереджена основна частина енергії спектра сигналу.

Енергія сигналу, що відсікається, призводить до появи похибки, яка в загальному вигляді виражається відношенням енергії відсіченої частини сигналу до загальної енергії сигналу. Але похибку зручніше виразити як дисперсію зведеної похибки

,

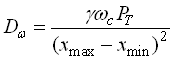де похибка дорівнює .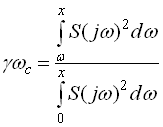    

Середня потужність сигналу може бути обчислена за формулою

.

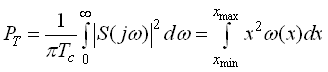Якщо відомі та спектри функції можна визначити частоту, яка обмежує спектр сигналу.