4.2 Дискретизація сигналів

Задача абсолютно точного відновлення сигналу на практиці зазвичай не ставиться, на відміну від задачі мінімального фізичного об’єму інформації, при якому зберігається можливість її відновлення в неперервній формі з визначеним допустимим значенням похибки. Така задача актуальна завжди, а особливо при дистанційних методах реєстрації та обробки інформації, передачі сигналів по каналах зв’язку і при підготовці інформації до тривалого зберігання. Одним з методів розв’язання цієї задачі є дискретизація сигналів за критерієм найбільшого відхилення.

В процесі дискретизації за критерієм найбільшого відхилення задається допустиме значення похибки відновлення сигналу . При відновленні сигналу неперервна функція апроксимується, як правило, степеневими поліномами -го порядку. Похибка відновлення функції поліномом визначається залишковим членом :

Крок дискретизації вибирається з умови забезпечення по всьому інтервалу визначення функції . Як правило, динаміка функції може суттєво змінюватися в різні моменти часу за інтервалом реєстрації, при цьому крок дискретизації також може змінюватися, за умови не перевищення заданої похибки на кожному кроці. При установленому значенні зменшення числа відліків забезпечується підвищенням степені апроксимувального багаточлена. На практиці зазвичай обмежуються сходинковим, лінійним та параболічним апроксимаційними поліномами відповідно нульового, першого і другого степенів.

Як було сказано вище, як інтерполювальні багаточлени використовують багаточлени Лагранжа, а як екстраполювальні багаточлени використовують багаточлени Тейлора. Для багаточлена Тейлора нульового степеня умови відновлення сигналу практично не відрізняються від багаточлена Лагранжа, за винятком напряму (від поточного зареєстрованого відліку і вперед до ). Для багаточленів Тейлора більш високих степенів при відновленні сигналу крім відліку використовуються також відповідні значення похідних в точці відліку. Відновлення сигналу багаточленами Тейлора відбувається без затримки в часі. Однак при використанні багаточленів вище нульового степеня для точного відновлення сигналу порівняно з інтерполяційними методами потрібно в два рази більш висока частота дискретизації.

Для багаточленів Лагранжа нульового степеня значення в момент часу на інтервалі між двома послідовними відліками функції приймається рівним відліку . Якщо відновлення сигналу проводити за двома відліками: , то при цьому ж кроці дискретизації похибка відновлення сигналу зменшується вдвічі. Але при використанні двох послідовних відліків краще застосовувати багаточлени Лагранжа першого степеня, тобто з’єднання двох послідовних відліків прямою лінією, що дає ще більше зменшення похибки відновлення аналогової форми сигналу.

Адаптивна дискретизація

Частота рівномірної дискретизації інформації розраховується за граничними значеннями частотних характеристик сигналів. Адаптивна дискретизація орієнтована на динамічні характеристики сигналу, що дозволяє забезпечити його відновлення при мінімальній кількості вибірок. В основі принципів адаптивної дискретизації лежить спостереження за поточною похибкою відновлення сигналу. Найбільш широке застосування отримали алгоритми дискретизації з адаптацією по довжині інтервалу апроксимації. Суть дискретизації полягає в послідовному нарощенні інтервалу апроксимації з неперервним порівнянням сигналу з відтворювальною функцією . При досягненні заданого значення? нарощення інтервалу зупиняють, і проводиться відлік значень , тобто дискретизація є нерівномірною. Для відтворення сигналів нерегулярної дискретизації зазвичай використовують степеневі алгебраїчні поліноми нульового чи першого степеня в інтерполяційному чи в екстраполяційному варіантах.

Найбільш простою є техніка адаптивної дискретизації з використанням багаточлена нульового степеня. На момент початку кожного інтервалу апроксимувальний поліном приймається рівним , обчислюється поточна різниця і проводиться порівняння її значення із заданим значенням. При фіксуванні рівності та заданого значення проводиться черговий відлік і починається наступний інтервал.

При використанні апроксимувального багаточлена першого степеня обчислюється значення де – похідна сигналу. Момент чергового відліку визначається виконанням рівності Варто мати на увазі, що даний алгоритм неефективний при наявності високочастотних завад, до яких досить чутлива операція диференціювання.

Дискретизація випадкових сигналів належить до класу непростих задач аналізу випадкових сигналів. Тому обмежимось лише згадуванням основних особливостей такого аналізу на прикладі дискретизації квантованих за рівнем випадкових сигналів.

Отож, для обчислення оптимального кроку рівномірної дискретизації достатньо знати лише величину інтервалу квантування та кореляційну функцію вимірюваного процесу.

При оперативних змінах із запам’ятовуванням результату лише останньої відлікової операції оптимальна тривалість наступного кроку практично не залежить від цього результату і дорівнює оптимальному кроку рівномірної дискретизації вимірюваного процесу.

В околі точки оптимуму існує деякий досить широкий інтервал приблизно рівнозначних значень кроку дискретності . Так в межах 10%-вих відхилень від оптимального значення зміни імовірнісного показника якості не перевищують 1%.

Оптимальний крок дискретизації визначається так

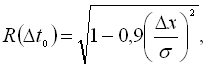
де – величина кванта;

– середньоквадратичне відхилення процесу.

Дана формула дозволяє визначити оптимальний крок дискретизації безпосередньо на графіку кореляційної функції. На практиці переважно використовують інше співвідношення:

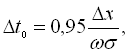
де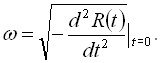

Усереднена за усіма номерам похибка визначається як

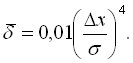
Варто зазначити, що при 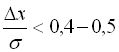розрахункову похибку оптимального значення критерію якості вимірювальної системи можна оцінити однією похибкою, яка складає приблизно 0,5%.