4.3 Квантування сигналів

Дискретизація аналогових сигналів з перетворенням в цифрову форму пов’язана з квантуванням сигналів. Суть квантування полягає в заміні нескінченної множини можливих значень функції, в загальному випадку випадкових, скінченною множиною цифрових відліків, і виконується округленням миттєвих значень вхідної функції в моменти часу до найближчих значень , де – крок квантування шкали цифрових відліків. Квантування з постійним кроком називають рівномірним. Математично операція квантування може бути виражена формулою:

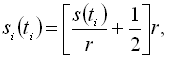
де результат обчислення в дужках округляється до цілого значення.

Квантування за амплітудою – це процес заміни реальних (виміряних) значень амплітуди сигналу значеннями, наближеними з деякою точністю. Кожен з можливих рівнів називається рівнем квантування, а відстань між двома найближчими рівнями квантування називається кроком квантування. У випадку лінійного розбиття амплітудної шкали на рівні, квантування називають лінійним (однорідним). На рис. 4.2. наведено приклад такого квантування.

Як бачимо, результатом такого оцифрування став ступінчатий сигнал, складений із прямокутників, кожен з яких має ширину, рівну величині кроку дискретизації, і висоту, рівну виміряному значенню амплітуди сигналу. Очевидно, що точність округлення залежить від вибраної кількості () рівнів квантування, яка, в свою чергу, залежить від кількості бітів (), відведених для запису значення амплітуди. Число називають розрядністю квантування (маючи на увазі кількість розрядів, тобто бітів, в кожному слові), а отримані в результаті округлення значень амплітуди числа – відліками чи семплами (от англ. «sample» – «замір»). Вважається, що квантування з розрядністю 16 біт залишається для слухача майже непомітним.

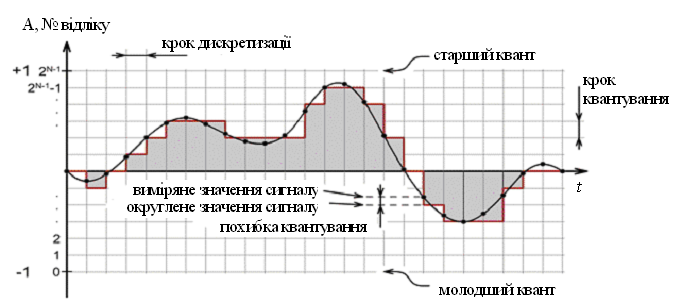
Рисунок 4.2 – Квантування неперервних сигналів по амплітуді

При квантуванні сигналів у великому динамічному діапазоні значень крок квантування може бути й нерівномірним, наприклад, логарифмічним, тобто пропорційним логарифму значень вхідного сигналу. Установлений діапазон шкали квантування від до і крок квантування визначають число поділок шкали 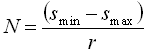і відповідно цифрову розрядність квантування. В результаті дискретизації й квантування неперервна функція замінюється числовою послідовністю {}. Похибка округлення знаходиться в межах і називається шумом квантування. Необхідна точність квантування оцінюється за впливом на подальшу обробку сигналів виниклого шуму квантування.

При достатньо малому кроці квантування будь-яке значення в його межах можна вважати рівноймовірним, при цьому значення розподілені за рівномірним законом.

Відповідно дисперсія та середнє квадратичне значення шуму квантування:

При заданому рівні шуму квантування з використанням попередньої формули неважко визначити допустиме значення кроку квантування.

Вхідний сигнал містить, як правило, адитивну суміш власне сигналу та завади з дисперсією відповідно . Якщо завади не корельовані із сигналом, то після квантування сумарна дисперсія шумів:

На практиці крок квантування вибирають зазвичай таким, щоб не відбувалось помітної зміни відношення сигнал/шум, тобто

Цифрове подання інформації можна коротко зробити таким чином. Якщо сигнал, який був дискретизований за часом і рівнем, потім подається у цифровому вигляді, то такий процес називається аналого-цифровим перетворенням. Оскільки в порівнянні із, наприклад, записаним на носії (касеті чи пластинці) аналоговим сигналом, цифровий запис характеризується високим відношенням сигнал-шум і широким динамічним діапазоном (відношенням мінімального сигналу до максимального неспотвореного сигналу) і забезпечує високу якість відтворення, наприклад, звуку. Але для відтворення записаного звуку його слід знову перевести в аналогову форму з допомогою цифро-аналогового перетворення, про що буде йти мова далі.

Перейдемо до розгляду позиційних систем числення. Позиційна система числення з основою має цифр , що звичайно позначають натуральні числа від 0 до . Ці записи та позначені ними числа – значення цих записів – називаються однорозрядними.

Цифри десяткової системи 0, 1, 2, … , 9 називаються арабськими, хоча й були запозичені арабами в індусів.

У програмуванні широко застосовується шістнадцяткова система, в якій перші 10 цифр арабські, а наступні шість, A, B, C, D, E, F, позначають числа, десятковий запис яких 10, 11, 12, 13, 14, 15, відповідно.

Число у -ковій системі позначається дворозрядним записом , число +1 – записом тощо. Наприклад, 10, 11, ... , 99 у десятковій системі, 10, 11 у двійковій, 10, 11, … , 1F, 20, … , FF у 16-ковій. Наприклад, 100, 101, … , 999 у десятковій системі, 100, 101, 110, 111 у двійковій, 100, 101, … , FFF у 16-ковій.

Наприклад, двійковий запис (10011)2 позначає число, яке в десятковому записі має вигляд 12⁴+02³+02²+12¹+12⁰=19. 16-ковий запис (1BC)16 позначає десяткове 1162+1116+12=444.

Права цифра в записі числа позначає кількість одиниць і називається молодшою, ліва – кількість чисел і називається старшою.

Ми звикли до десяткового подання чисел, і саме воно, головним чином, використовується в програмах, але в комп'ютері числа, як правило, подаються в двійковій системі. Таким чином, виникає необхідність створювати двійкове подання числа за його десятковим записом і навпаки.

За -ковим записом натурального числа можна побудувати десяткове подання, обчисливши значення полінома за допомогою операцій множення та додавання в десятковій системі.

-кове подання чисел, менших 1, має вигляд , де – -кові цифри. Цей запис позначає дійсне число – значення виразу

Нагадаємо, що якщо основа має прості дільники, відмінні від 2 і 5, то число зі скінченним -ковим записом зображується нескінченним, але періодичним десятковим дробом. Якщо ж простими дільниками є тільки 2 і 5, то й десятковий дріб скінченний.

Перейдемо до цифрового кодування. При цифровому кодуванні дискретної інформації застосовують потенціальні й імпульсні коди.

У потенціальних кодах для подання логічних одиниць і нулів використовується тільки значення потенціалу сигналу, а його перепади, що формують закінчені імпульси, до уваги не беруться. Імпульсні коди дозволяють подати двійкові дані або імпульсами певної полярності, або частиною імпульсу – перепадом потенціалу певного напрямку.

Вимоги до методів цифрового кодування

При використанні прямокутних імпульсів для передачі дискретної інформації необхідно вибрати такий спосіб кодування, який одночасно досягав би декількох цілей:

а) мав при одній і тій же бітовій швидкості найменшу ширину спектра результуючого сигналу;

б) забезпечував синхронізацію між передавачем і приймачем;

в) мав здатність розпізнавати помилки;

г) мав низьку вартість реалізації.

Більш вузький спектр сигналів дозволяє на одній і тій же лінії (з однієї і тією же смугою пропускання) домагатися більш високої швидкості передачі даних. Крім того, часто до спектра сигналу висувається вимога відсутності постійної складової, тобто наявності постійного струму між передавачем і приймачем. Зокрема застосування різних трансформаторних схем гальванічної розв'язки перешкоджає проходженню постійного струму.

Синхронізація передавача і приймача потрібна для того, щоб приймач точно знав, у який момент часу необхідно зчитувати нову інформацію з лінії зв'язку. Ця проблема в мережах важить більше, ніж при обміні даними між близько розташованими пристроями, наприклад між блоками усередині комп'ютера чи між комп'ютером і принтером. На невеликих відстанях добре працює схема, що базується на окремій тактовій (синхронізуючій) лінії зв'язку (рис. 4.3), тому інформація знімається з лінії даних тільки в момент приходу тактового імпульсу.

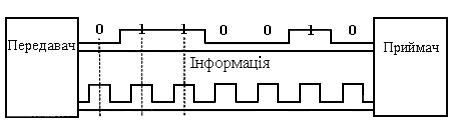
Рисунок 4.3 – Синхронізація приймача і передавача на невеликих відстанях

У мережах використання цієї схеми спричиняє труднощі через неоднорідність характеристик провідників у кабелях. На великих відстанях нерівномірність швидкості поширення сигналу може привести до того, що тактовий імпульс прийде настільки пізніше чи  раніше відповідного сигналу даних, що біт даних буде пропущений чи врахований повторно. Іншою причиною, через яку у мережах відмовляються від використання тактуючих імпульсів, є економія провідників у дорогих кабелях.

Тому в мережах застосовуються самосинхронізуючі сигнали, які несуть для передавача інформацію про те, у який момент часу потрібно здійснювати розпізнавання чергового біта (чи декількох біт, якщо код орієнтований більш ніж на два стани сигналу). Будь-який різкий перепад сигналу – що називається фронтом – може нести інформацію для синхронізації приймача з передавачем.

При використанні синусоїд як несучого сигналу результуючий код має властивість самосинхронізації, тому що зміна амплітуди несучої частоти дає можливість приймачу визначити момент появи вхідного коду.

Розпізнавання і корекцію перекручених даних складно здійснити засобами фізичного рівня, тому найчастіше цю роботу беруть на себе протоколи, що лежать вище: канальний, мережний, транспортний чи прикладний. З іншого боку, розпізнавання помилок на фізичному рівні заощаджує час, тому що приймач не чекає повного переміщення кадру в буфер, а відбраковує його відразу при розпізнаванні помилкових бітів усередині кадру.