 | |
|
Автори:
Злепко С. М., Коваль Л. Г., Гаврілова Н. М., Тимчик І. С. |
|
Навчальний посібник |
1.7 Основні рівняння комп'ютерної томографіїРаніше було дано поняття комп'ютерної томографії як одного з методів обчислювальної У цьому розділі на прикладах найбільш розповсюджених апаратних реалізацій комп'ютерної томографії: рентгенівської, ЯМР і ультразвукової покажемо, якими основними рівняннями вони можуть бути описані. Наведемо спочатку опис способу одержання основного рівняння комп'ютерної томографії для рентгенівської томографії [7]. Рентгенівська комп'ютерна томографія. Тут носієм інформації є рентгенівські фотони, поле випромінювання яких буде характеризуватися функцією потоку випромінювання І (r, ?, E), де вектор r – просторові координати, вектор ? – кутові координати, а Е – енергія фотонів. Функцію щільності джерел рентгенівських фотонів позначимо через I0 (r, ?, E). Тоді поширення рентгенівських фотонів у речовині з лінійним коефіцієнтом послаблення f (r, Е) можна описати за допомогою рівняння переносу
де ∑0 – макропереріз релеївського і комптоновского розсіювання. У багатьох випадках перебування оператора Sf-1 в явному вигляді ускладнене. Тому природно використовувати такі фізичні наближення процесу переносу випромінювання, для яких перебування явного виду оператора Sf-1 було б досить простим. Нехай, наприклад, функцію потоку випромінювання можна подати у вигляді ряду Неймана:
де Ip — потік первинних (нерозсіяних) рентгенівських фотонів, Іn — потік n-разово розсіяних рентгенівських фотонів (п = 1, 2, ...). Відмітимо, що вибір наближення до Sf може визначити як схему сканування рентгенівського томографа, так і вимоги до його вузлів. Наприклад, якщо ми використовуємо точкове колімоване моноенергетичне джерело рентгенівського випромінювання, а схему сканування сконструюємо так, щоб вплив розсіювання був досить малим, то оператор Sf можна взяти у вигляді:
де с>0 – потужність джерела, δ(u) – дельта-функція Дірака, r0 – координати джерела, Ω0 – напрямок колімації джерела, Е0 – енергія рентгенівських фотонів джерела. За допомогою оператора Sf вигляду (1.6) можна приблизно описати процеси переносу рентгенівського випромінювання в біотканинах, що відбуваються, наприклад, у комп'ютерних томографах СТ-1010 фірми EMI Ltd. (Великобританія), СРТ-1000, СРТ-1000М (СРСР) і подібних до них, реалізують так звану паралельну схему сканування з поступально-обертальним рухом джерела і зв'язаного з ним одного чи декількох детекторів випромінювання. Типовим для цієї схеми є те, що вона заснована на врахуванні тільки первинних фотонів джерела. З (1.6) легко бачити, що задача перебування оператора Sf -1, оберненого до Sf, досить проста. Дійсно, розв'язуючи рівняння (1.6) відносно Ip (r, ?, Е) і здійснюючи заміну змінних r=(x,y)®(l,θ), де ρ=(l,θ) – нормальні координати прямої на площині, одержуємо
де c0 – потік джерела випромінювання, Г (l, θ) – лінія, уздовж якої поширюється випромінювання. Для зазначеної схеми сканування характерним є поступально-обертальний рух лінії пари джерело-детектор (а отже, і Г(ρ)). Щоб це формалізувати, розглянемо сім'ю ліній (Г(ρ)), інваріантну щодо обертання навколо початку координат, що збігається з деякою заданою точкою всередині досліджуваного об'єкта. Нехай U – оператор, що переводить функцію Ip(l, θ, Е0) у функцію Р-оператора (1, θ): Тоді, у випадку використання моноенергетичного джерела рентгенівського випромінювання з (1.7) і (1.8) одержимо основне рівняння комп'ютерної томографії
Велика різноманітність способів апаратної реалізації рентгенівської комп'ютерної томографії з'являється і при використанні розсіяних фотонів. Наприклад, схеми сканування, що використовують так звану віялову геометрію в томографах IV покоління, характеризуються наявністю широкого пучка рентгенівських фотонів, що випускаються джерелом. Така схема покладена в основу комп'ютерного томографа Рfizer 0450 (США) та ін. На відміну від раніше згаданих томографів, в останніх не можна обійтися без обліку впливу розсіювання при переносі випромінювання, що залежно від використовуваної енергії джерела може бути або релеївським, або комптонівським. Нехай функція потоку випромінювання І подана у вигляді (1.5). Тоді рівняння для In n-разово розсіяних рентгенівських фотонів має вигляд:
де δn0 – символ Кронекера. Рішення цього рівняння можна записати у вигляді
де , Використовуючи формули (1.10), (1.11), можна звести рішення рівняння переносу до обчислення послідовності багаторазових інтегралів In. Таким чином, в даному випадку оператор Sf-1 задається неявно. Основне рівняння комп'ютерної томографії буде мати вигляд
де U – оператор, що переводит Легко побачити, що рівняння (1.12) нелінійне відносно функції f (r, Е). Фізичні процеси, що відбуваються при поширенні рентгенівських фотонів в біотканинах, можна формально описати так, що основне рівняння комп'ютерної томографії буде лінійним рівнянням відносно деякого ефективного коефіцієнта послаблення випромінювання. В цьому випадку оператор Sf-1 можна взяти у вигляді
Тут F0(δ, Е, t) – деяка позитивна функція; t – вектор, компоненти якого є числовими чи функціональними параметрами, що характеризують властивості досліджуваного об'єкта, джерела і детекторів випромінювання, а також конструкцію комп'ютерного томографа; f(r, Е) – просторово-енергетичний розподіл лінійного коефіцієнта ослаблення рентгенівського випромінювання. Якщо функція f(r, Е) подана у вигляді
де f1 (E) — монотонно cпадаюча аналітична функція на відрізку [Е1, Е2], мала в деякому розумінні порівняно з
Ультразвукова томографія. Цей термін потребує пояснення, оскільки він використовується в технічній літературі для характеристики різних способів діагностики об'єктів за допомогою ультразвуку УЗ (US). На нашу думку, ультразвукова томографія – це не зовсім вдалий термін, прийнятий для позначення способів ультразвукової діагностики, у яких значне використання сучасної обчислювальної техніки для знаходження рішень різних зворотних задач. Проаналізувати всі мислимі способи ультразвукової томографії не є можливим. Обмежимося розглядом двох принципово різних підходів до ультразвукової томографії. Ці підходи засновані на різних допущеннях, що дозволяють розв'язувати хвильове рівняння, що описує акустичне поле в неоднорідному середовищі. Математичний опис поширення гармонічних хвиль у неоднорідному середовищі без джерел подається рівнянням Гельмгольца
де u (х, у, z) – скалярна хвильова функція, k (x, у, z) - хвильове число, дорівнює ?/с (x, у, z). Суть першого підходу полягає в такому: нехай функція u(х, у, z) подана у вигляді
де φ (x, у, z) – ейконал (фаза хвилі). Нехай Sf (φ) = ( Очевидно, рівняння Sf (φ)=0 відносно ? є нелінійним рівнянням у частинних похідних першого порядку. Якщо траєкторія променя Г(ρ) (
Введемо тотожний оператор U. Тоді основне рівняння ультразвукової томографії має вигляд
Оператор Т може служити досить гарною математичною моделлю ультразвукової комп'ютерної томографії лише в тих випадках, коли досліджуваний об'єкт однорідний за щільністю, варіації показника заломлення досить малі і явища дифракції неістотні. Безумовно, ці вимоги різко звужують область застосування цієї моделі, а ультразвукові томографи, засновані на її використанні, малоефективні на практиці. У роботі вивчався вплив зазначених факторів на якість томограм і були зроблені такі висновки. На частотах, характерних для медичних досліджень (від 2 до 5 МГц), позначається вплив дифракційних ефектів. Якщо варіації Для розв'язання рівняння (1.16) можна скористатися наближеннями Ритова і Борна. У цьому і полягає суть другого підходу. Наприклад, у наближенні Ритова не робиться ніяких припущень про довжину хвилі випромінювання. Тому можна сподіватися врахувати і дифракційні ефекти. Однак при цьому потрібна достатня малість величин ( Загальна схема одержання основного рівняння комп'ютерної томографії. Нехай функції ?, ? і р несуть характеристики відповідно поля випромінювання, джерел випромінювання і результатів томографічних вимірів, а функція f характеризує шукану щільність просторового розподілу цікавлячої нас фізичної величини [7]. Припустимо, що функції ?, ?, р і f суть елементи відповідно лінійних нормованих просторів Ф, ?, P та F. Нехай задано сім'ю {Sf} операторів Sf : Ф ? ?, що залежать, як від параметра, від функції f
В багатьох випадках оператори Sf такі, що існують оператори Sf-1, обернені Sf і обмежені з Ψ в Ф (наприклад, коли Sf - диференційні оператори). У цих випадках розв'язок рівняння (1.20) можна записати у вигляді
В комп'ютерній томографії типові випадки, коли вимірюють не функції φ, а їхні непрямі прояви - інтеграли від φ по деяких множинах. Формально це означає, що існує оператор U, який діє з простору Ф в простір F такий, що
Підставляючи (5.18) в (5.19), одержуємо співвідношення
яке ми будемо називати основним рівнянням (відносно f) комп'ютерної томографії. Зауважимо, що співвідношення (1.20)-(1.22) описують набагато ширший клас задач. Відповідно до загальної схеми, можна одержати основні рівняння різних видів комп'ютерної томографії. При цьому основні рівняння визначаються вибраними фізико-математичними моделями цих видів і можуть бути як лінійними, так i нелінійними задачами відносно просторового розподілу фізичної величини, що нас цікавить. ЯМР-томографія. В описаних вище рентгенівських і ультразвукових схемах сканування досліджуваних об'єктів використовуються механічні системи, а явища ослаблення (чи кінематичні особливості) при поширенні випромінювання в об'єктах є основою для застосування принципу комп'ютерної томографії. ЯМР-томографія заснована на взаємодії досить малих магнітних полів, що змінюються в часі, із слабкозв'язаними з решіткою, ядрами деяких атомів (наприклад, водню) у м'яких біотканинах. З метою наочного пояснення сутності ЯМР розглянемо таку фізичну модель. Уявімо собі вовчок, що обертається навколо своєї осі, причому його вісь відхилена від вертикалі на деякий кут. Таке обертання дає уявлення про прецесію. За певних умов вектори ядерних моментів прецесують відносно вектора магнітної індукції В0. Частота прецесії пропорційна магнітній індукції В0 поля, у яке поміщають досліджуваний об'єкт. При цьому спіни протонів орієнтуються вздовж магнітного поля (поляризація). Якщо тепер на постійне магнітне поле В0 накласти неоднорідне поле G (за допомогою градієнтних систем), то протони в різних точках простору будуть прецесувати з різними частотами. Можна так спотворити постійне однорідне магнітне поле, що з однаковими частотами будуть прецесувати вектори ядерних моментів, розташовані на певних множинах, наприклад, на лініях чи площинах. Якщо за допомогою радіочастотних імпульсів вивести потім протони з положення рівноваги, то вони будуть випромінювати енергію у вигляді сигналів вільної індукції. У такий спосіб реалізується принцип комп'ютерної томографії [7]. Сукупність способів апаратної реалізації принципів комп'ютерної томографії, заснованих на використанні явища ЯМР, будемо називати ЯМР-томографією. Властивості досліджуваних об'єктів, що вивчаються за допомогою ЯМР-томографії, характеризуються рівноважною ядерною намагніченістю Ме(r) і часом повздовжньої Т1(r) та поперечної Т2(r) релаксації, що визначають час «повернення» спіна ядра атома до рівноважного стану. Величина Ме(r) характеризує просторовий розподіл релаксуючих ядер атомів досліджуваної речовини, а величини Т1(r), Т2(r) - зв'язки ядер атомів із ґраткою. Характерною рисою ЯМР-томографії є можливість визначення самих величин Ме(r), Т1(r), Т2(r), а також функціоналів від них за непрямою інформацією. Конкретний спосіб ЯМР-томографії визначається як використовуваним фізичним наближенням, так і експериментальними можливостями. Покажемо на деяких прикладах, як може бути отримане основне рівняння ЯМР-томографії. Перше, що необхідно з'ясувати – це як формалізувати основні фізичні процеси ЯМР. Іншими словами, як побудувати оператор Sf, де під символом f будемо розуміти розподіл будь-якої із зазначених фізичних величин. У рентгенівській томографії оператор Sf являв собою інтегро-диференційний оператор Больцмана, за допомогою якого описувався процес переносу рентгенівських фотонів у речовині. У випадку ЯМР-томографії оператор Sf повинен характеризувати часові зміни ядерної намагніченості спінової макросистеми залежно від величин Ме, Т1, Т2. Звертаючись до теорії ЯМР у рідких неметалевих парамагнетиках, якими є і м'які біотканини, можна побудувати оператор Sf. Для цього будемо виходити з рівняння Блоха, справедливого для магніторозбавлених зразків:
де B(t,r) – індукція повного магнітного поля, M(t, r) – намагніченість досліджуваного об'єкта, M={Mx, My, Mz}, γ – гіромагнітне відношення. Рівняння (1.23) можна фізично інтерпретувати в такий спосіб. Нехай на спінову систему, що складається з ансамблю спінів ядер атомів, ідентичних один одному, з моменту t=0 впливає збуджуюче її магнітне поле В1 (вхідний сигнал). У результаті цього впливу спінова система переходить до нового квантового стану. Після припинення впливу B1 вона починає повертатися до рівноважного стану за законом (1.23). Отже, оператор S1 у даному випадку визначається рівнянням (1.23). Насправді, повне магнітне поле В(t,r) звичайно являє собою суму постійного магнітного поля В і поля, утвореного так званими градієнтними полями G. Нехай |B0Z| >> |Gx|, |Gy|. Тоді
Під дією такого поля в точці з координатами r вектор намагніченості буде прецесeсувати з частотою
Розв'язуючи рівняння Блоха (1.23) з врахуванням (1.24) (чи (1.25)), одержимо вираз для зміни намагніченості в процесі релаксації:
де Нехай Ψ=B(t, r), φ=M(t, r), f=Me(r). Тоді згідно з (1.23) оператор S1 має вигляд
а для оператора Sf-1 справедливе подання
Враховуючи те, що оператор U визначається співвідношенням
де p(t, ρ) – сигнал вільної індукції, отримаємо основне рівняння ЯМР-томографії у вигляді
Таким чином, як видно з (1.26) і (1.28), якщо час Т2 досить великий порівняно з часом реєстрації сигналу вільної індукції, то величиною, що визначається в процесі ЯМР-томографії, є просторовий розподіл рівноважної ядерної намагніченості. Можливі й інші (відмінні від томографічного) методи вимірювань в ЯМР-діагностиці, що визначаються характером імпульсної послідовності, тобто послідовності з ВЧ-імпульсів і градієнтних імпульсів [10]. Становить інтерес і інша математична модель ЯМР-томографії [11], що не використовує рівняння Блоха. Розглянемо зразки, які містять ядра атомів речовини, що мають власний магнітний момент. Нехай виконується нерівність
де ΔЕ – зміна енергії при переходах між квантовими станами, k – стала Больцмана, Т – температура досліджуваного зразка. У цих умовах спіни ядер не змінюються в ході досліджень. Будемо вважати, що: 1) досліджуваний зразок є магніторозбавленим, тобто таким, що усі ядра атомів парамагнітні, а релаксація кожного спіна ядра не залежить від релаксації інших спінів; 2) спіни ядер, що беруть участь у релаксації, складають спінову підсистему, взаємодіючу з іншим оточенням – граткою, яку будемо вважати термостатом, тобто такою системою, що має необмежено велику теплоємнісь; 3) існує механізм, що досить швидко повертає термостат у рівноважний стан. У цих припущеннях можна дати таке трактування магнітної системи. При виконанні умови (1.29) повний гамільтоніан H? магнітної системи має вигляд [12]:
де І – набір усіх ядерних спінів, q – набір інших немагнітних координат (наприклад, спіни електронів), HS – спін-гамільтоніан, що описує спінову систему ядер, HSP – гамільтоніан, що описує спін-гратковий вплив, HР - гамільтоніан, що описує "гратку" (фононну систему). Якщо магнітна система взаємодіє із змінними магнітними полями, то в (1.30) треба додати член ?(I, t), що описує цю взаємодію, тобто
З умови магніторозбавленості випливає [12], що рівняння релаксації, які містять спінові змінні для кожного ядра, можуть бути відділені так, що результат для всього зразка є сумою результатів для кожного ядра. Розглянемо рівняння, що визначає релаксацію будь-якої фізичної величини Q(t), що залежить від спінових змінних. Скористаємося для цього теорією Хаббарда [12]. Нехай ρ(t) – повна матриця щільності магнітної системи, ?s(t) – спінова матриця щільності, ?ор – рівноважна матриця щільності гратки. Тоді, для ?s(t) одержуємо рівняння
де N, R – релаксаційні оператори. Припустимо, що ?s(t) знайдена з рішення відповідної задачі для (1.32). Тоді [12]
де (Q(t)) - середнє значення величини Q(t), що характеризує квантову систему, Sp – слід матриці. Звідси видно, що для того, щоб знайти середнє значення спостережуваної фізичної величини треба знайти ρs(t). Однак ця задача є досить складною. Тому, залишаючись у рамках тих же припущень, побудуємо іншу, спрощену модель. Нехай η(Ij) (j=1, 2, ...) – спостережувані фізичні величини для j-го ядерного спіна, Q – спостережувана фізична величина для всієї спінової ядерної системи. Тоді з умови магніторозбавленості зразка випливає, що
Іншими словами, якщо ?(Ij) є ЯМР-спектр j-го ядерного спіна, то спектр спінової системи запишемо у вигляді суми спектрів складових її спінів. Це співвідношення основний наслідок умови магніторозбавленості зразка, який і буде використаний в подальших міркуваннях. Відомо, що коли спектр простий, то застосовна теорія Блоха-Редфілда [12], відповідно до якої можна знайти форму лінії поглинання K(ω, ξ), де ω – частота, ξ – півширина лінії. Наприклад, якщо Розглянемо тепер процеси релаксації магнітної системи. Затухання поперечної складової її магнітного моменту можна пояснити впливом двох груп процесів: 1) однорідного ущільнення; 2) неоднорідного ущільнення. До процесів, відповідальних за однорідне ущільнення, відносяться такі, які призводять до виникнення флуктуючих локальних магнітних полів поблизу кожного ядерного спіна. До процесів, що відповідають за неоднорідне ущільнення, відносяться такі, які призводять до виникнення статичних локальних магнітних полів поблизу кожного центра релаксації. Будемо вважати, що кожен ядерний спін у процесі релаксації утворить сукупність δ-подібних ліній, кожна з яких має ту ж форму K(ω, ξ), але з різними значеннями ξ. При цьому сама функція K(ω, ξ) визначається тільки процесами однорідного ущільнення. У процесі спін-спінової і спін-граткової взаємодії всі δ-подібні лінії поєднуються в лінії скінченної ширини. Результатом цього є обвідна сім'ї всіх δ-подібних ліній. Нехай φ(ξ) – функція щільності розподілу півширин усіх ?-подібних ліній у спектрі, утворених магнітною системою при релаксації. Зауважимо, що хоча при одержанні цього співвідношення ми не враховували явний вплив процесів неоднорідного ущільнення, вони проте можуть бути враховані ним. Наприклад, отриману обвідну S0(?) для складної системи спектрів можна проінтерпретувати як спектр хімічно нееквівалентних ядер, що належать одній і тій же або різним молекулам. У цьому випадку рівняння (1.35) визначає спектр хімічного зсуву.
Перейдемо до аналізу впливу інших процесів, що приводять до неоднорідного ущільнення. Відмітимо відразу, що конкретний механізм процесу неоднорідного ущільнення визначається характером задачі, що розглядається. Наприклад, якщо постійне магнітне поле В0 просторово неоднорідне, то це призводить до виникнення відмінних одне від одного локальних магнітних полів поблизу кожного ядерного спіна. У цьому випадку механізм процесу неоднорідного ущільнення обумовлений просторовою неоднорідністю магнітного поля В0. Спектр ЯМР, визначений рівнянням (1.35), враховує взаємодії ядерних спінів один з одним і з граткою. Тому надалі можна вважати, що у випадку просторово однорідного магнітного поля В0 магнітна система характеризується спектром (1.35) і цей спектр можна описати однорідною формою сигналу спінів, що мають однакову резонансну частоту ?. Введемо функцію G(?), що характеризує розподіл ядерних спінів за резонансними частотами (обумовлене неоднорідним ущільненням). Вона являє собою щільність імовірності того, що ядерний спін має резонансну частоту ?. Нехай Š(ω)-спектр ЯМР, спотворений неоднорідним ущільненням. Встановимо зв'язок між величинами Š(ω) і S0(ω). Припустимо, що спінова система лінійна. Це припущення виправдане принаймні для магніторозбавлених зразків. Сигнал S0(ω) будемо називати вхідним сигналом системи, a Š(ω) – вихідним. Наша ціль полягає у побудові оператора системи, що ставить у відповідність вхідному сигналу S0 вихідний сигнал Š. Нехай формальний зв'язок між Š(ω) і S0(ω) задається лінійним диференціальним рівнянням n-го порядку відносно Š(ω) з неперервними коефіцієнтами:
Тоді якщо однорідне рівняння АŠ=0 з відповідними крайовими умовами має тільки тривіальний розв'язок, то для будь-якої неперервної функції S0(?) має місце співвідношення
де G(ω, ω′) – функція Гріна оператора, породженого рівнянням (1.36) з відповідними граничними умовами. Співвідношення (1.37) можна розглядати як рівняння відносно S0(ω). При цьому функція розподілу резонансних частот є функцією Гріна. У магніторозбавленних зразках кожен ядерний спін "поводиться" незалежно від інших [12]. Це дозволяє вважати спінову систему просторово інваріантною. Тому функція Гріна G залежить лише від різниці змінних ω-ω′ і, отже, співвідношення (1.37) буде мати вигляд
На практиці функція G може бути приблизно визначена з результатів вимірювань сигналу ЯМР від хімічно однорідного зразка (тобто такого, усі ядра якого хімічно еквівалентні). Точність такого способу знаходження G(ω) тим вища, чим краще спектр S0 еталонного зразка апроксимує ?-подібну лінію. На практиці, враховуючи кінцеву роздільну здатність спектрометрів ЯМР, досить підібрати еталонний зразок, ширина спектральної лінії якого не більша роздільної здатності за частотою. В протилежному випадку потрібно теоретично розрахувати спектр S0(ω) від еталонного зразка і розв'язувати рівняння (1.38) відносно функції G(ω). Нехай g(r) – розподіл концентрації хімічного елемента (сполуки), ядра атомів якого піддаються впливу в процесі ЯМР-томографії, а
де Контрольні запитання 1. Поясніть роботу рентгенодіагностичного апарата? 2. Чим категорія кіл АД відрізняється від категорії ВД? 3. В чому полягає суть принципів ALARA і ALATA? 4. Поясніть схему взаємодії елементів цифрової рентгенографічної системи. 5. В чому полягає принцип утворення пошарових зображень? 6. Перерахуйте основні етапи отримання томограми. 7. В чому полягає принцип рентгенівської томографії? 8. Поясніть суть процесу формування томографічного зрізу. 9. Поясніть принцип роботи комп'ютерного томографа. 10. Що таке ЕПТ?
|

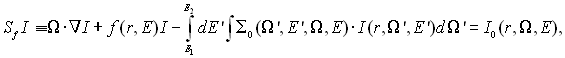
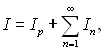
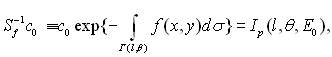
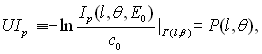 (1.8)
(1.8)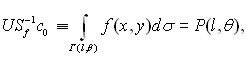
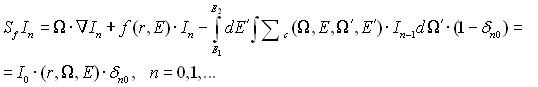
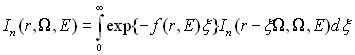
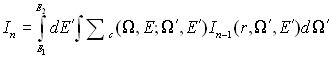 ь функцію потоку I(r, ?, Е) рентгенівського випромінювання у вимірюваний при томографічних дослідженнях сигнал P.
ь функцію потоку I(r, ?, Е) рентгенівського випромінювання у вимірюваний при томографічних дослідженнях сигнал P.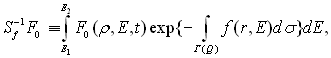
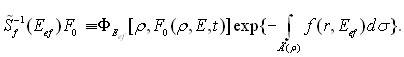
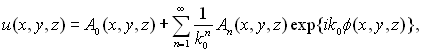
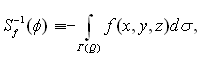
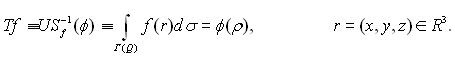
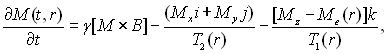
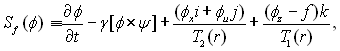
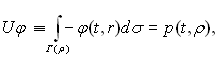
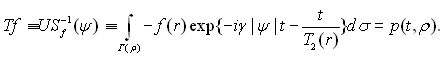
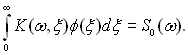
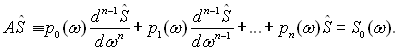
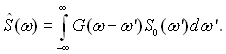
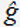 (ρ) –інтеграл від g(r) по сімейству різноманітностей {Г(ρ)}. Позначимо f=g(r), p=
(ρ) –інтеграл від g(r) по сімейству різноманітностей {Г(ρ)}. Позначимо f=g(r), p=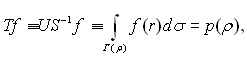
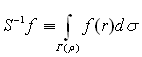 , U – тотожний оператор.
, U – тотожний оператор.