1.5. Незалежні і залежні події, умовні ймовірності. Теореми про добуток подій

Означення 1. Подія А називається незалежною (independent) від події В, якщо ймовірність появи події А не залежить від того, відбулась подія В чи не відбулась.

Теорема 1. Якщо випадкові події А і В незалежні, то імовірність суміщення подій А і В дорівнює добутку ймовірностей появи цих подій.

Означення 2. Подія А називається залежною (dependent) від події В, якщо ймовірність події А змінюється в залежності від того, відбулась подія В чи не відбулась.

Розглянемо два приклади:

I. Дослідом є кидання двох монет.

Розглядаються події:

А – поява герба на одній монеті;

В – поява герба на другій монеті.

В цьому випадку ймовірність події А не залежить від того, відбулась подія В чи не відбулась; подія А не залежить від події В.

II. Задача з так званої “схеми урн”.

В урні дві білих кульки і одна червона. Дві особи виймають із урни по одній кульці.

Розглянемо події:

А – поява білої кульки у першої особи;

В  поява білої кульки у другої особи.

Імовірність події А до того, як відомо що-небудь про подію В, рівна . Якщо стало відомо, що подія В відбулась, то імовірність події А стає рівною , з чого робимо висновок, що подія А залежить від події В.

Означення 3. Ймовірність події А, обчислена при умові, що мала місце інша подія В, називається умовною ймовірністю (conditional probability) події А і позначається .

Для другого прикладу маємо:

, .

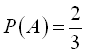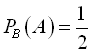Умову незалежності події А від події В можна записати у вигляді:

.

Теорема 2. Імовірність добутку двох подій дорівнює добутку імовірності однієї з них на умовну імовірність другої, яка обчислена при умові, що перша мала місце:

.

Доведення. Нехай можливі виходи досліду зводяться до n випадків.

Нехай появі події А сприяють m випадків. Існують випадки, які сприяють і події А, і події В одночасно. Нехай число таких випадків l. Тоді

;

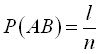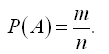
Якщо відомо, що А відбулась, то можливих випадків, при яких відбувається А і з них l сприяють події В, а значить .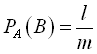

Тоді одержимо :

,

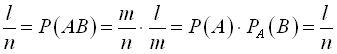що й потрібно було довести.

Теорему можна записати так: .

Якщо ж А не залежить від В, то і і одержимо результат теореми 1: .

Приклад. На конвеєрі проходить 10 валиків, з них 5 конусних (conical), 7 еліптичних (elliptic). Робітник бере один валик, потім другий. Знайти ймовірність того, що перший з узятих валиків – конусний, а другий – еліптичний.

Розв’язання.

Імовірність того, що перший валик конусний 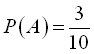. Імовірність того, що другий валик еліптичний (подія В), при умові, що перший конусний, є умовною імовірністю.

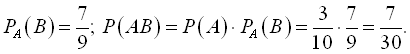
Або навпаки

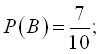
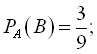
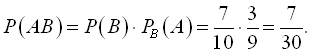
Ймовірність добутку декількох подій:

.

Ймовірність кожної наступної за порядком події обчислюється при умові, що всі попередні мали місце.