2.3. Неперервні випадкові величини (н. в. в.)

Крім дискретних випадкових величин, які приймають окремі числові значення і утворюють скінченну або нескінченну послідовність чисел, часто також зустрічаються випадкові величини, можливі значення яких заповнюють деякий інтервал.

Прикладом такої випадкової величини може бути відхилення від номіналу певного розміру деталі при правильно налагодженому процесі. Такі випадкові величини не можуть бути задані за допомогою закону розподілу ймовірностей не можна кожному значенню поставити у відповідність імовірність.

Функція розподілу задається аналогічно:

.

Функція задана для всіх і її значення в точці х рівне імовірності того, що випадкова величина прийме значення, менше х.

Всі рівності і властивості 1, 2 (записані для д. в.) справедливі і в цьому випадку. Доведення аналогічне випадку дискретної величини. Випадкова величина називається неперервною (continuous), якщо для неї існує невід’ємна, кусково-неперервна функція така, що для всіх виконується рівність:

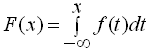. (2.1)

Функція називається густиною (щільністю) (the density) розподілу ймовірностей або коротко густиною розподілу (the density distribution). Якщо , то одержимо:

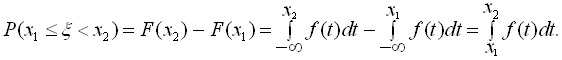(2.2)

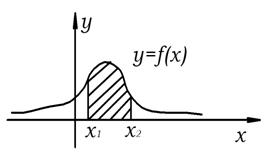
Виходячи з геометричного змісту інтеграла як площі, можна скaзати, що ймовірність виконання нерівності рівна площі криволінійної трапеції з основою , обмеженою зверху кривою (рис. 2.3). Далі , тоді

.

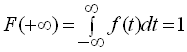Звідси слідує:

Знайдемо як похідну інтеграла за змінною верхньою границею, вважаючи неперервною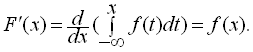

Для неперервної випадкової величини функція неперервна в довільній точці х, де функція неперервна. Це випливає з того, що в цих точках диференційовна. Часто називають інтегральною функцією розподілу (integral distribution function), а диференціальною функцією розподілу     (the differential distribution functionу).

Із формули (2.2), приймаючи х₁=х, х₂=х+х і в силу неперервності маємо:

.

Таким чином, імовірність того, що неперервна випадкова величина може прийняти окреме числове значення х, дорівнює нулю:

Отже,      Зауваження. Відомо, якщо подія неможлива, то імовірність її появи рівна нулю. У випадку неперервної випадкової величини число її можливих значень нескінченне. Імовірність того, що ця величина прийме яке-небудь конкретне значення, рівна нулю. Однак з цього не випливає, що ця подія неможлива, тому що в результаті випробування вона може набути довільне зі своїх значень. Нульова імовірність може бути не лише для неможливої, але і для можливої події. Поняття “події можливі, але які мають нульову імовірність” здається на перший погляд парадоксальним. В дійсності воно не більш парадоксальне, ніж уявлення про тіло, що має певну масу, але жодна з точок, що знаходиться всередині тіла, не має певної скінченної маси. Як завгодно малий об’єм, виділений із тіла, має певну скінченну масу; ця маса наближається до нуля при зменшенні об’єму і в границі рівна нулю для точки. Аналогічно для неперервно розподіленої випадкової величини ймовірність попадання на як завгодно малий інтервал відмінна від нуля в той час, як імовірність попадання в строго визначену точку рівна нулю. У випадку неперервної випадкової величини є сенс говорити про ймовірність попадання випадкової величини в інтервал, а не про ймовірність того, що вона прийме певне конкретне значення.

Так, при виготовленні валика нас не цікавить імовірність того, що його діаметр буде рівний номіналу. Для нас важлива імовірність того, що діаметр валика не виходить із поля допуску.

У ХVIII ст. швидко почала розвиватися теорія похибок (помилок) спостережень. “Похибка вимірювання в залежності від випадку може приймати різні значення” – основна думка вчених, які займалися теорією випадкових величин, яка на той час була поки що невідомою для них. Вперше така думка була висловлена Галілеєм задовго до робіт відомих математиків, що займалися проблемою неперервної випадкової величини. Він же ввів у обіг поняття “випадкова” і “систематична” похибка вимірювання.

Похибка вимірювання є випадковою величиною з певним невідомим (поки що) розподілом ймовірності.

У своїх роботах Я. Бернуллі розглянув кількість появ події А в п незалежних дослідах, тобто випадкову величину, яка може набувати значення 0, 1, 2, …, п з імовірностями, які ми обчислюємо за формулами Бернуллі.

Спочатку вчені вважали, що можливі значення похибок вимірювань складають арифметичну прогресію з невизначеною, але дуже малою різницею. Відмовившись від такої думки, науковці почали припускати, що можливі значення, які приймають похибки спостережень, заповнюють певний відрізок, а ймовірності можливих значень визначалися через визначення густини розподілу.

В перших роботах Я. Бернуллі питання густини розподілу розглядається з деякою неточністю. У роботах Лапласа, Гаусса поняття густини розподілу було означено більш точно і наближалося до сучасного. Зокрема Лаплас у своїй відомій книзі “Аналітична теорія ймовірностей” наводить формулу для обчислення густини розподілу суми, маючи густини розподілу доданків; вчений вміло оперує з густинами розподілу, однак дослідник не вводить поняття випадкової величини. Лаплас обходив введення цього поняття або шляхом використання теорії похибок вимірювань, або використовуючи “мову” математичного аналізу.

Поняття випадкової величини не було введено аж до першої пол. Х1Х ст. Його введенню спонукали дослідження бельгійського математика-дослідника А. Кетле (1796-1874). Вчений помітив зв’язок між розмірами тварин та їх віком. Цей зв’язок підлягав нормальному закону розподілу, для якого потрібно було введення випадкової величини.

Крім А. Кетле ряд інших вчених розглядали цікаві задачі, розв’язання яких вимагало введення поняття випадкової величини, серед них К. Ф. Гаусс, Д. К. Максвел та ін.

Першу спробу ввести поняття випадкової величини здійснив Пуаcсон у 1832 р. у своїй роботі “Про ймовірність середніх результатів досліджень”. Однак у нього в роботі не зустрічається термін “випадкова величина”, натомість присутнє поняття “деяка річ”, яка може набувати значення , , …, відповідно з імовірностями , , ….

Згодом у своїх роботах П. Л. Чебишов, О. М. Ляпунов використовують термін “величина” (variable).