1.3.     Основні властивості функцій алгебри логіки

Функції кон’юнкції та диз’юнкції мають ряд властивостей, аналогічних властивостям звичайних операцій множення та додавання. Легко переконатися в тому, що для цих функцій мають місце: комутативний закон для кон’юнкції та диз’юнкції (1.1):

Для доведення цього закону необхідно замість аргументів підставляти відповідно значення 0 або 1, а потім робити порівняння стовпців в таблицях для функцій, що знаходяться в лівій та правій частинах розглядуваного співвідношення.

Функції кон’юнкції та диз’юнкції підпорядковуються асоціативному закону (1.2):

          ;

          .

Дистрибутивний закон (1.3):

          ;

          .

Перевіримо справедливість цього закону для диз’юнкції відносно кон’юнкції шляхом порівняння стовпців в таблицях для функцій, що знаходяться в лівій та правій частинах розглядуваного співвідношення:

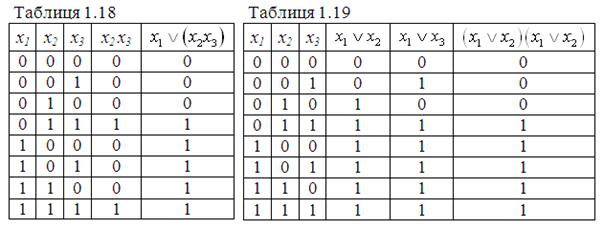
Збіг крайніх стовпців в побудованих таблицях 1.18, 1.19 доводить наше твердження.

Розглянемо тепер ряд простих, але вельми важливих для функцій кон’юнкції та диз’юнкції співвідношень, які в подальшому будемо використовувати в задачах мінімізації логічних функцій:

–     закони логічного додавання та множення з константою одиниці (1.6), (1.8):

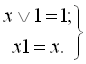
–     закони логічного додавання та множення з константою нуля (1.5), (1.7):

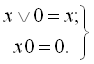
–     закон ідемпотентності (1.4):

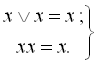
–     закон виключеного третього та закон протиріччя (1.9), (1.10):

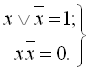
–     закон подвійного заперечення (1.11):

          .

Таблиця 1.28

–     формули де Моргана (1.13), (1.14):

          ;

          .

Доведення правила де Моргана наведені в табл. 1.29.

Таблиця 1.29

З таблиці 1.29 видно, що при різних значеннях і права і ліва частини однакові. Формули де Моргана можна використовувати і для випадку, коли функція має більше двох аргументів, нижче наведені відповідні співвідношення:

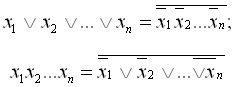               (1.23)

Аналогічним чином доводяться інші тотожності.

Властивості функції додавання за модулем 2 та функції імплікації часто бувають корисними при аналізі та синтезі різних дискретних приладів.

Для функції додавання за модулем 2 мають місце переставний та сполучний закони, а також розподільний закон відносно кон’юнкції:

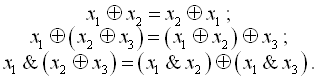               (1.24)

Мають місце також очевидні співвідношення:

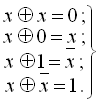               (1.25)

Крім того, має місце формула

               (1.26)

На відміну від усіх розглянутих раніше функцій для імплікації не мають місця переставний та сполучний закони:

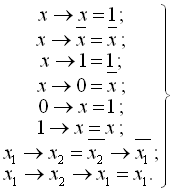               (1.27)

Функції диз’юнкції та кон’юнкції можуть бути виражені через імплікацію таким чином:

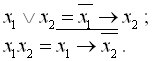               (1.28)

Доведення співвідношень (1.28) наведені в табл. 1.30 та 1.31.

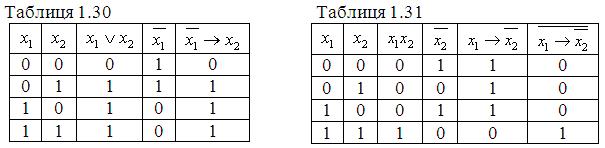
З таблиць 1.30, 1.31 видно, що при різних значеннях х та у права і ліва частина формул (1.28) однакові.

Для функцій штрих Шеффера і операція Пірса має місце переставний закон

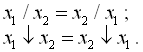               (1.29)

Сполучний закон для них не виконується:

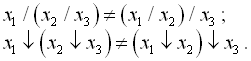
Мають місце такі очевидні співвідношення:

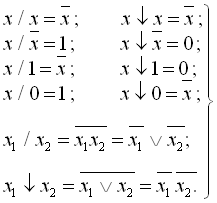               (1.30)

В силу відсутності сполучного закону дії розкриття дужок та винесення за дужки для функцій штрих Шеффера і операція Пірса специфічні та виконуються за такими правилами:

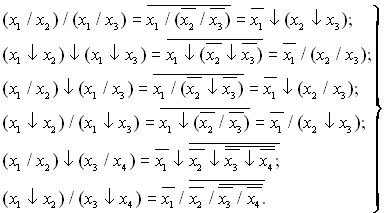               (1.31)

Доведення справедливості цих співвідношень аналогічне. Доведемо, наприклад, справедливість рівності

          .

Використовуючи два останніх співвідношення з (1.30), перетворимо обидві частини цього співвідношення таким чином:

          .

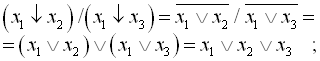
Збіг лівої та правої частин після проведення еквівалентних перетворень доводить рівність.

Функції штрих Шеффера і операція Пірса пов’язані між собою співвідношеннями, аналогічними до формул де Моргана для функцій кон’юнкції та диз’юнкції:

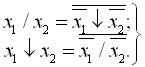               (1.32)

Для доведення справедливості першого з цих співвідношень зазначимо, що на основі двох останніх рівностей з (1.30) можна перше зі співвідношень (1.31) переписати у такому вигляді:

          ;

          .

Оскільки отримане співвідношення є формулою де Моргана, то перше зі співвідношень (1.31) справедливе. Для другого співвідношення доведення аналогічне.