1.2 Основні закони алгебри логіки та їх використання для подання одних функцій логіки через інші

Вперше логічні функції були використані в алгебрі логіки, початок якій покладено працями англійського математика Дж. Буля, її також називають булевою алгеброю або алгеброю висловлень.

Під висловленням розуміється будь-яке твердження, яке може бути істинним або хибним.

Істинному висловленню приписується 1, хибному – 0. Висловлення можуть бути простими і складними. Складні висловлення складаються з простих.

Для об’єднання простих висловлень в складні використовуються логічні зв’язки, що відповідають логічним функціям, аргументами яких є прості висловлення.

Логічний зв’язок “І” (кон’юнкція). Кон’юнкцією називають складне висловлення, що містить 2 або більше простих висловлень і яке є істинним тоді і лише тоді, коли істинними є прості висловлення, і хибним, якщо хоч одне з простих висловлень хибне.

Кон’юнкція являє собою логічний зв’язок “І” (див. табл. 1.5).

З’єднання двох висловлень читається як “ і ”. Позначається або .

Таблиця 1.5

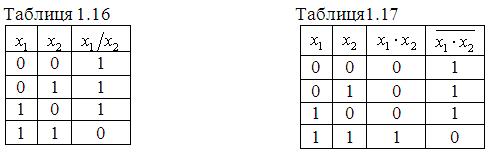
Логічний зв’язок “АБО” (диз’юнкція). Диз’юнкцією називають складне висловлення, що містить декілька простих висловлень і яке є істинним тоді, коли істинним буде хоч одне з простих висловлень, які входять в це складне висловлення, і хибним, якщо всі прості висловлення хибні.     

Диз’юнкція являє собою логічний зв’язок “АБО” (табл. 1.6) і позначається . Читається “ або ”.

Таблиця 1.6

Логічний зв’язок “НЕ” (заперечення). Логічний зв’язок “НЕ” означає заперечення висловлення і читається “НЕ ”, позначається або Ш (табл. 1.7)

Таблиця 1.7

Запереченням висловлення називають складне висловлення “НЕ ”, яке є істинним, коли хибне, і хибним, коли істинне.

Для зручності подальших викладок використаємо позначення: “∙” – кон’юнкція, “” – диз’юнкція і “” – заперечення.

Булевою алгеброю називається множина , що складається не менше ніж з двох елементів, на якій визначені три операції – диз’юнкції (), кон’юнкції (), заперечення (). Для будь-яких елементів виділяємо набір незалежних властивостей, які вважають аксіомами булевої алгебри, а саме:

–     закон комутативності:

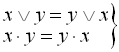          ;      (1.1)

–     закон асоціативності:

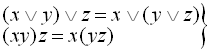          ;      (1.2)

–     закон дистрибутивності:

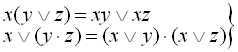          ;      (1.3)

     для спрощення формул крім аксіом використовують такі співвідношення або закони алгебри логіки:

–     логічне додавання до нуля:

          ;     (1.4)

–     логічне додавання до одиниці:

          ;     (1.5)

–     логічне множення на 0:

          ;     (1.6)

–     логічне множення на 1:

          ;     (1.7)

–     закон протиріччя:

          ;     (1.8)

–     закон виключеного третього:

          .     (1.9)

Всі інші закони є наслідком зазначених вище:

–     закон ідемпотентності:

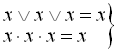          ;     (1.10)

–     закон подвійного заперечення:

          ;     (1.11)

–     закон поглинання (х поглинає у):

          ;     (1.12)

–     закон де Моргана:

               (1.13)

               (1.14)

–     наслідки законів де Моргана:

          ;     (1.15)

          .     (1.16)

За допомогою розглянутих співвідношень можна виконувати різні тотожні перетворення булевих виразів.

При цьому порядок виконання дій такий:

При відсутності дужок виконуються операції заперечення, потім кон’юнкції, останніми – диз’юнкції.

Подання одних функцій алгебри логіки через інші

1. Операція заборони:

          .     (1.17)

Для доведення цього і наступних співвідношень будемо підставляти в ліву і праву частини виразу окремі значення аргументів і перевіряти правильність рівності.

Таблиця 1.8    

Таблиця 1.9

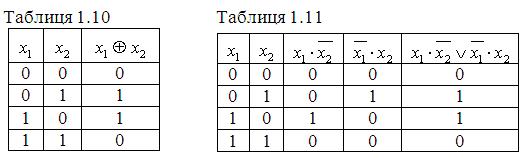
2. Сума за модулем 2:

          .     (1.18)

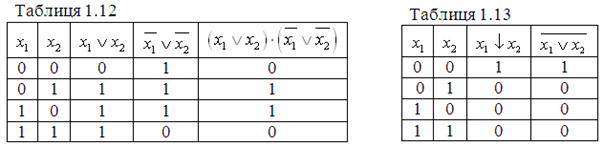
3. Операція Пірса:

               (операція АБО-НЕ).      (1.19)

4. Логічна рівнозначність:

          .     (1.20)

Справедливість першої рівності може бути встановлена безпосередньо по таблицях істинності функції логічної рівнозначності і суми по модулю 2; наступних рівностей - шляхом інвертування лівої і правої частин виразу і перетворення за формулами де Моргана.

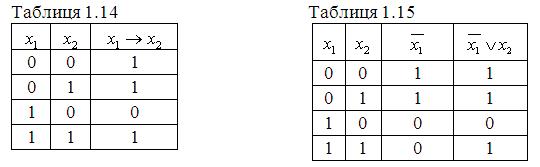
5. Імплікація:

          .     (1.21)

6. Функція Шеффера:

          (операція І-НЕ).     (1.22)