2.3     Способи переходу від нормальної до досконалої форми логічної функції

Перехід від нормальної до досконалої форми логічної функції здійснюється за таблицею, аналітично або графічно.

Перехід від нормальної до досконалої форми логічної функції за таблицею

Будь яку логічну функцію можна легко виразити як диз’юнкцію конституент одиниці, відповідно до тих наборів, на яких функція дорівнює 1. В більш загальному вигляді можна записати це таким чином [9]:

          ,

     де σ_і = 0,1;

Ця форма і є ДДНФ. Зауважимо, що набори, на яких функція f набуває значення 1, часто називаються одиничними, інші – нульовими наборами. Виписувати в ДДНФ має сенс тільки конституенти одиниці (в літературі має ще іншу назву – мінтерм), які відповідають одиничним наборам.

Таблиця 2.1

Приклад 1. Випишемо ДДНФ для функцій, заданих таблицею істинності (табл. 2.1).

;

.

Інша відома форма носить назву досконалої кон’юнктивної нормальної форми (ДКНФ). Вона будується аналогічно ДДНФ.

ДКНФ подається як кон’юнкція конституент нуля (в літературі має ще іншу назву – макстерм), відповідних нульовим наборам функції.

Приклад 2. Для розглянутих вище функцій f₁, f₂ М(х₁, х₂, х₃) (див. табл. 2.1) побудуєм ДКНФ.

;

.

Аналітичний спосіб переходу від нормальної до досконалої форми логічної функції

Досконала нормальна форма на відміну від нормальної завжди містить диз’юнкції (ДДНФ) або кон’юнкції (ДКНФ) лише максимального рангу r. Це дає можливість проводити перехід за такими правилами.

Для переходу від довільної ДНФ до ДДНФ r-го рангу необхідно кон’юнкції, які входять до ДНФ, k-го (k) рангу послідовно множити на логічний вираз , де ѕ одна із змінних, яка не входить в дану кон’юнкцію. Число таких перетворень для кожної кон’юнкції повинно бути (r-k).

Приклад 3. Перетворити в ДДНФ логічну функцію, задану в ДНФ: fДНФ.

1.     Використовуючи закони:

, ,

і тотожність алгебри логіки, перетворимо кон’юнкції заданої функції в мінтерми 3-го рангу:

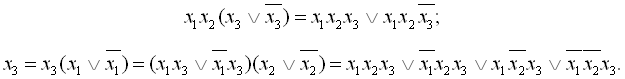
2.     В результаті перетворень отримані мінтерми з’єднаємо символом диз’юнкції і, використовуючи тотожність отримаємо

          fДДНФ.

Для переходу від довільної КНФ до ДКНФ r-го рангу необхідно диз’юнкції, які входять в КНФ, k-го рангу послідовно додавати з логічним виразом , де ѕ одна із змінних, яка не входить в дану диз’юнкцію. Число таких перетворень для кожної диз’юнкції повинно бути (r-k).

Приклад 4. Перетворити в ДКНФ логічну функцію, задану в КНФ:

          fКНФ

1.     Використовуючи закони

          ,

і тотожність алгебри логіки, перетворимо диз’юнкції заданої функції в макстерми 3-го рангу:

          ;

2.     В результаті перетворень отримані макстерми з’єднаємо символом кон’юнкції і, використовуючи тотожність,

отримаємо:

Найбільш наочним і простим графічним способом перетворення логічної функції з нормальної форми в досконалу є карти Карно-Вейча.

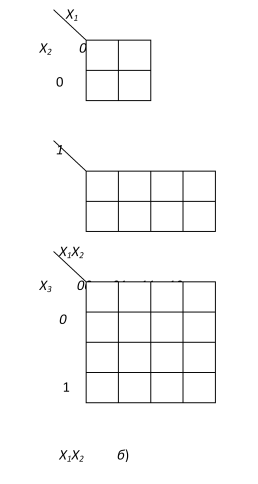
Карта Карно – графічне подання всіх мінтермів (2n) для даного числа змінних (n). Кожний мінтерм зображується у вигляді клітинки, розміщеної так, що мінтерми, які знаходяться у сусідніх клітинках, відрізняються лише однією змінною. На рис. 2.1 подано зображення карт Карно для функцій двох, трьох і чотирьох змінних. Змінні написані по обидві сторони діагональної риски в лівому кутку карти. Значення змінних позначаються на зовнішньому боці карти за допомогою двійкових цифр: 0 – відповідає інверсному значенню змінної, а 1 – прямому. Така умова дає можливість легко уявити для кожної клітинки карти Карно відповідний їй мінтерм.

У картах Карно сусідніми також вважаються граничні клітинки кожного стовпчика або рядка, оскільки розташовані в них мінтерми відрізняються значенням однієї змінної.

Алгоритм перетворення логічної функції з ДНФ в ДДНФ за допомогою карти Карно полягає в такому:

Для заданої логічної функції зобразити карту Карно.

Поставити в клітинках карти Карно одиницю для тих мінтермів, в склад яких входять кон’юнкції заданої функції.

Відмічені одиницею мінтерми зўєднати символами диз’юнкції – це і буде ДДНФ заданої логічної функції.

Приклад 5. За допомогою карти Карно перетворити логічну функцію з ДНФ в ДДНФ.

Розв’язок. 1. Для заданої логічної функції для відповідного перетворення будуємо карту Карно (рис. 2.2), на якій одиницею відмічені мінтерми, в склад яких входять кон’юнкція і змінна

2.     Запишемо значення логічної функції в ДДНФ, з’єднавши відмічені мінтерми символами диз’юнкції:

          fДДНФ

Перехід від КНФ логічної функції до ДКНФ може бути також здійснений за допомогою карти Карно. Пояснимо це на прикладі.

Приклад 6. Перетворити в ДКНФ логічну функцію, задану в КНФ:

          fКНФ

Розв’язок. 1. Від заданої функції в КНФ отримаємо її інверсне значення:

2.     Для отриманої логічної функції будуємо карту Карно (рис. 2.3), на якій одиницею відмічаємо мінтерми, що включають в себе логічні змінні і

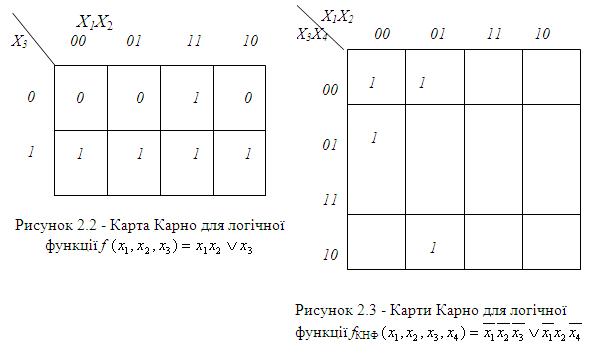
3.     Користуючись картою Карно (рис. 2.3), запишемо інверсне значення логічної функції в ДКНФ:

4.     На основі тотожності інверсне значення для цієї функції має вигляд

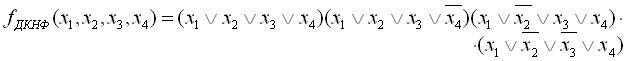
і буде являти собою задану логічну функцію в ДКНФ.