2.4 Функціонально повні системи булевих функцій
Будь-яка булева функція може бути подана аналітично однією з розглянутих в п. 2.3 нормальних форм. Останні використовують обмежене число елементарних булевих функцій. Наприклад, для ДДНФ такими функціями є «кон’юнкція», «диз’юнкція» і «заперечення». Отже, існують системи булевих функцій, за допомогою яких можна аналітично подати будь-яку скільки завгодно складну булеву функцію. Проектування цифрових автоматів основане на знанні таких систем булевих функцій. Останнє особливо важливе для розробки комплектів інтегральних мікросхем, з яких можна побудувати довільний цифровий автомат.
Означення. Функціонально повною системою булевих функцій (ФПСБФ) називається сукупність таких булевих функцій ![]() , що довільна булева функція
, що довільна булева функція ![]() може бути записана у вигляді формули через функції цієї сукупності.
може бути записана у вигляді формули через функції цієї сукупності.
Проблема функціональної повноти є центральною проблемою функціональних побудов в алгебрі логіки. Розв’язання цієї задачі основане на понятті замкнутого відносно операції суперпозиції класу функцій [9].
Клас булевих функцій, функціонально замкнутий за операцією суперпозиції, є множина функцій, будь-яка суперпозиція яких дає функцію, що також належить цій множині. Серед функціонально замкнутих класів виділяють класи особливого типу, які називаються передповними. Проведені дослідження показали, що передповних класів п’ять, а для побудови ФПСБФ необхідно і достатньо, щоб її функції не містилися повністю в жодному з п’яти передповних класів.
Перерахуємо передповні класи булевих функцій:
1. Булеві функції, що зберігають константу 0;
2. Булеві функції, що зберігають константу 1;
3. Самодвоїсті булеві функції;
4. Лінійні булеві функці;
5. Монотонні булеві функції.
Означення. До булевих функцій, які зберігають константу 0, відносять такі булеві функції ![]() , для яких справедливе співвідношення
, для яких справедливе співвідношення ![]() .
.
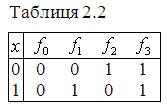
Прикладами булевих функцій, що зберігають константу 0, є функції ![]() і
і ![]() (див. табл. 2.2) і функції
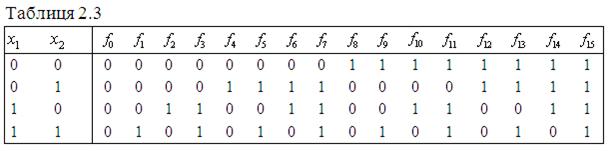
(див. табл. 2.2) і функції ![]() ,
, ![]() , …
, …![]() (див. табл. 2.3).
(див. табл. 2.3).
Означення. До булевих функцій, що зберігають константу 1, відносять такі булеві функції ![]() , для яких справедливо співвідношення
, для яких справедливо співвідношення ![]() .
.
Прикладами булевих функцій, що зберігають константу 1, є функції ![]() і
і ![]() (табл.2.2) і функції
(табл.2.2) і функції ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (див. табл. 2.3).
(див. табл. 2.3).
Для введення поняття класу самодвоїстих функцій, використаємо поняття двоїстих функцій.
Означення. Булеві функції ![]() і
і ![]() називаються двоїстими одна одній, якщо виконується співвідношення:
називаються двоїстими одна одній, якщо виконується співвідношення:
![]() .
.
Двоїстими є функції ![]() і
і ![]() ,
, ![]() і
і ![]() ,
, ![]() і
і ![]() тощо (див. табл. 2.3).
тощо (див. табл. 2.3).
Означення. До самодвоїстих булевих функцій відносять такі булеві функції, які є двоїстими відносно самих себе, тобто справедливе співвідношення![]() . Будемо називати протилежними наборами набір (
. Будемо називати протилежними наборами набір (![]() ,
, ![]() , …,
, …, ![]() ) і набір (
) і набір (![]() ,
, ![]() , …,
, …, ![]() ), тоді означення самодвоїстих функцій дамо таке.
), тоді означення самодвоїстих функцій дамо таке.
Означення. Булева функція називається самодвоїстою, якщо на будь-яких двох протилежних наборах вона приймає протилежні значення.
Самодвоїстими є функції ![]() ,
, ![]() ,
, ![]() ,
, ![]() (див. табл. 2.3).
(див. табл. 2.3).
Означення. До лінійних булевих функцій відносять такі булеві функції, які можуть бути подані у вигляді
![]() ,
,
де ![]() , а
, а ![]() — операція «сума за mod 2».
— операція «сума за mod 2».
Лінійними є булеві функції f0, f3, f5, f6, f9, f10, f12, f15.
Перш ніж ввести поняття класу монотонних булевих функцій, дамо таке означення.
Означення. Двійковий набір ![]() не менше двійкового набору
не менше двійкового набору ![]() , (тобто
, (тобто ![]() ), якщо для кожної пари
), якщо для кожної пари ![]()
![]() справедливе співвідношення
справедливе співвідношення ![]() .
.
Так, набір 1011 ![]() 1010. Разом з тим набори 1011 і 0100 непорівнянні в тому значенні, що для них не виконується ні співвідношення
1010. Разом з тим набори 1011 і 0100 непорівнянні в тому значенні, що для них не виконується ні співвідношення ![]() , ні
, ні ![]() .
.
Означення. Булева функція ![]() називається монотонною, якщо для будь-яких двох наборів
називається монотонною, якщо для будь-яких двох наборів ![]() і
і ![]() таких, що
таких, що ![]() має місце нерівність
має місце нерівність ![]() .
.
Монотонними є булеві функції ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , (див. табл. 2.3). Разом з тим функція
, (див. табл. 2.3). Разом з тим функція ![]() з табл. 2.3 не є монотонною, оскільки
з табл. 2.3 не є монотонною, оскільки ![]() , хоча набір
, хоча набір ![]() менше, ніж набір
менше, ніж набір ![]() .
.
Наведемо без доведення формулювання теореми про функціональну повноту.
Теорема. Для того, щоб система ![]() булевих функцій була функціонально повною, необхідно і достатньо, щоб ця система містила хоча б одну булеву функцію, що не зберігає константу 1, хоча б одну булеву функцію, що не зберігає константу 0, хоча б одну несамодвоїсту булеву функцію, хоча б одну нелінійну булеву функцію і хоча б одну немонотонну булеву функцію.
булевих функцій була функціонально повною, необхідно і достатньо, щоб ця система містила хоча б одну булеву функцію, що не зберігає константу 1, хоча б одну булеву функцію, що не зберігає константу 0, хоча б одну несамодвоїсту булеву функцію, хоча б одну нелінійну булеву функцію і хоча б одну немонотонну булеву функцію.
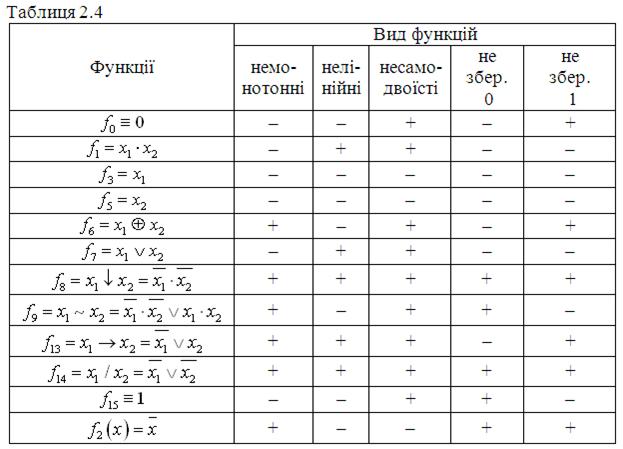
Розглянемо приклади ФПСБФ. Для зручності викладу матеріалу зведемо елементарні булеві функції двох змінних і деякі функції однієї змінної в табл. 2.4. З табл. 2.4 видно, що кожна з функцій ![]() ,
, ![]() є ФПСБФ. Іншими словами, використовуючи, наприклад, тільки булеву функцію
є ФПСБФ. Іншими словами, використовуючи, наприклад, тільки булеву функцію ![]() — «штрих Шеффера», можна записати у вигляді формули будь-яку булеву функцію. Табл. 2.4 дозволяє одержати і інші ФПСБФ. Ознакою функціональної повноти є, очевидно, наявність плюса в кожному стовпці табл. 2.4, хоча б для однієї з складових системи булевих функцій. До таких ФПСБФ, найпоширеніших в практиці побудови цифрових автоматів, слід віднести:
— «штрих Шеффера», можна записати у вигляді формули будь-яку булеву функцію. Табл. 2.4 дозволяє одержати і інші ФПСБФ. Ознакою функціональної повноти є, очевидно, наявність плюса в кожному стовпці табл. 2.4, хоча б для однієї з складових системи булевих функцій. До таких ФПСБФ, найпоширеніших в практиці побудови цифрових автоматів, слід віднести: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() , де символами
, де символами ![]() ,
, ![]() ,
, ![]() ,
, ![]() , 1, позначені булеві функції: «диз’юнкція», «кон’юнкція», «сума за mod 2», «заперечення», «константа 1», відповідно.
, 1, позначені булеві функції: «диз’юнкція», «кон’юнкція», «сума за mod 2», «заперечення», «константа 1», відповідно.
Принцип двоїстості булевих функцій
Введене поняття двоїстих булевих функцій дозволяє сформулювати принцип двоїстості, що полягає в такому: якщо формула ![]() реалізує булеву функцію
реалізує булеву функцію ![]() , то формула
, то формула ![]() , одержана з
, одержана з ![]() заміною функцій
заміною функцій ![]() на двоїсті функції
на двоїсті функції ![]() , відповідно реалізує функцію
, відповідно реалізує функцію ![]() , двоїсту функції
, двоїсту функції ![]() . Формулу
. Формулу ![]() * називають двоїстою
* називають двоїстою ![]() . Для формул над множиною
. Для формул над множиною ![]() принцип двоїстості може бути сформульований так: для отримання формули
принцип двоїстості може бути сформульований так: для отримання формули ![]() , двоїстої формулі
, двоїстої формулі ![]() , достатньо у формулі
, достатньо у формулі ![]() усюди замінити 0 на 1, 1 на 0, & на
усюди замінити 0 на 1, 1 на 0, & на ![]() ,
, ![]() на &.
на &.
Приклад. Із співвідношення ![]() застосуванням принципу двоїстості виходить співвідношення
застосуванням принципу двоїстості виходить співвідношення ![]() . Принцип двоїстості дозволяє майже в два рази скоротити зусилля на виведення співвідношень при розгляді властивостей елементарних булевих функцій.
. Принцип двоїстості дозволяє майже в два рази скоротити зусилля на виведення співвідношень при розгляді властивостей елементарних булевих функцій.