Розділ 3 МЕТОДИ МІНІМІЗАЦІЇ ЛОГІЧНИХ ФУНКЦІЙ

Розглянемо основні методи мінімізації логічних функцій в класі диз’юнктивних нормальних форм. При цьому під мінімальними будемо розуміти диз’юнктивні нормальні форми (ДНФ), які містять найменшу сумарну кількість змінних (букв) в усіх диз’юнктивних членах.

Нагадаємо деякі поняття.

Елементарним добутком (кон’юнкцією) будемо називати кон’юнкцію декількох різних змінних, що взяті із запереченнями або без них. Наприклад і тому подібні.

Диз’юнктивною нормальною формою (ДНФ) називають диз’юнкцію елементарних кон’юнкцій.

Мінімальною диз’юнктивною нормальною формою булевої функції називають ДНФ, яка містить найменьшу кількість букв ( відносно всіх інших ДНФ, які представляють задану функцію).

Функція називається імплікантою функції , якщо на будь-якому наборі значень змінних виконується умова

          .

Наведемо два твердження (без доведення), які є корисними при отриманні мінімальних ДНФ:

1) диз’юнкція будь-якого числа імплікант булевої функції також є імплікантою цієї функції;

2) будь-яка булева функція еквівалентна диз’юнкції всіх своїх імплікант; така форма подання булевої функції називається скороченою ДНФ.

Простими імплікантами логічної функції називають такі елементарні кон’юнкції, які самі входять до даної функції, тобто є імплікантами функції , але ніяка їх власна частина не є імплікантою функції .

Прості імпліканти являють собою найкоротші елементарні добутки, що входять до даної логічної функції. Звідси випливає, що логічна функція дорівнює диз’юнкції всіх простих імплікант.

Будь-яка логічна функція має нескінченну множину простих імплікант, кількість яких менша або дорівнює кількості конституент одиниці в досконалій диз'юнктивній нормальній формі (ДДНФ).

     3.1 Метод Квайна

Розглянемо метод отримання скороченої ДНФ, який називається методом Квайна. Цей метод базується на перетвореннях досконалої диз’юнктивної нормальної форми за допомогою операції неповного склеювання та поглинання.

Операція (повного) склеювання визначається співвідношенням:

               (3.1)

Справедливість даного виразу випливає з такого перетворення:

          .

Операція поглинання визначається співвідношенням:

          .     (3.2)

Кажуть, що член поглинається членом . Справедливість сказаного випливає з перетворень:

          .

Операція неповного склеювання, що застосована в методі Квайна, визначається формулою

          ,

яка може бути отримана з формул (3.1) і (3.2)

          .

Теорема Квайна

Якщо в досконалій диз’юнктивній нормальній формі логічної функції провести всі операції неповного склеювання, а потім всі операції поглинання, то вийде скорочена диз’юнктивна нормальна форма цієї функції, тобто диз’юнкція всіх її простих імплікант [1, 2].

З теореми Квайна випливає: якщо функція задана у довільній формі, то її слід перетворити в досконалу ДНФ, застосувати функцію розгортання, і лише після цього проводити операції склеювання і поглинання.

Приклад

Знайти скорочену ДНФ функції

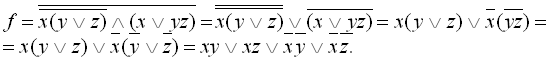
Застосувавши розгортку знаходимо ДДНФ

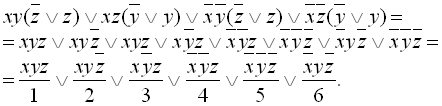
Проводимо склеювання:

1 – 2

2 – 6

1 – 3

3 – 4

4 – 5

5 – 6

Для пошуку мінімальних форм зручно користуватися імплікантною таблицею, яка подана в табл. 3.1, у вертикальні та горизонтальні входи якої записуються конституенти 1-ці та прості імпліканти заданої функції.

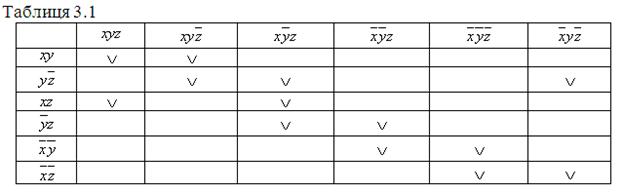
Отримано дві еквівалентні мінімальні диз’юнктивні нормальні форми.

Таким чином при мінімізації за методом Квайна припускається, що вихідна функція задана в досконалій диз’юнктивній нормальній формі (ДДНФ). Задача мінімізації за методом Квайна полягає в попарному порівнянні всіх імплікант, що входять до ДДНФ, з метою виявлення можливості поглинання будь-якої змінної:

          .

Ця процедура знижує ранг термів та продовжується до тих пір, поки не залишиться жодного члена, який допускає поглинання з будь-яким іншим термом. Терми, які піддалися поглинанню, відмічаються. Невідмічені терми являють собою первинні імпліканти.

Отриманий логічний вираз не завжди виявляється мінімальним, тому досліджується можливість подальшого спрощення. Для цього складається таблиця, в рядках якої записуються знайдені первинні імпліканти, а в стовпцях вказуються терми вихідного рівняння. Клітинки цієї таблиці відмічаються у випадку, коли первинна імпліканта входить до складу будь-якого терма. Після цього задача спрощення зводиться до того, щоб знайти таку мінімальну кількість первинних імплікант, які покривають всі стовпці.

Розглянемо мінімізацію логічної функції, яка задана у вигляді:

          .

Задачу мінімізації функції відповідно до алгоритму Квайна розв’язуємо в декілька етапів.

Етап 1. Знаходження первинних імплікант.

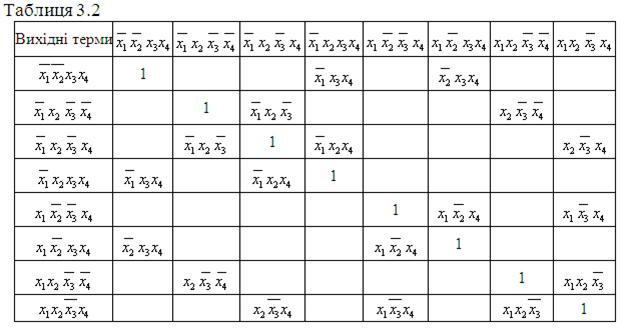
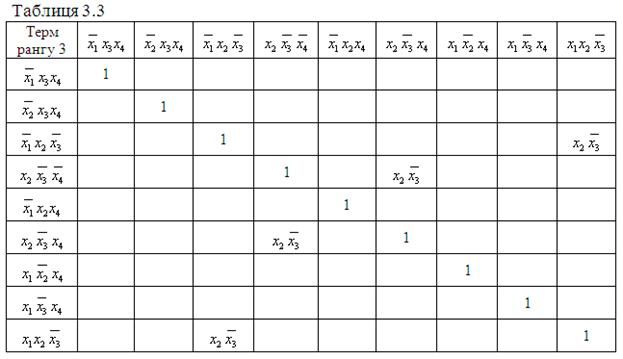
Складаємо таблицю 3.2 і знаходимо імпліканти четвертого і третього рангу, тобто знижуємо ранг термів, які входять до ДДНФ. Потім складаємо іншу таблицю (табл. 3.3), яка містить всі терми, що не піддалися поглинанню, а також первинні імпліканти третього рангу. Складання таблиць продовжується до тих пір, поки буде неможливо застосувати правило поглинання. В нашому завданні можна дійти до первинної імпліканти другого рангу (табл. 3.3).

Таким чином первинні імпліканти найменшого рангу – .

Етап 2. Встановлення позначок.

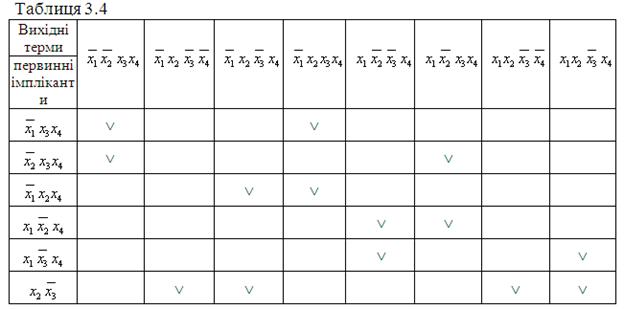
Складаємо таблицю, кількість рядків якої дорівнює кількості отриманих первинних імплікант, а кількість стовпців збігається з кількістю мінтермів ДДНФ. Якщо в деякий мінтерм ДДНФ входить будь-яка з первинних імплікант, то на перетині відповідного стовпця і рядка ставиться позначка (табл. 3.4).

Етап 3. Знаходження суттєвих імплікант.

Якщо в будь-якому із стовпців таблиці 3.4 є тільки одна позначка, то первинна імпліканта у відповідному рядку є суттєвою, оскільки без неї не буде отримана вся множина заданих мінтермів. В таблиці 3.4 суттєвою імплікантою є терм . Стовпці, які відповідають суттєвим імплікантам, з таблиці викреслюються.

Етап 4. Викреслення зайвих стовпців.

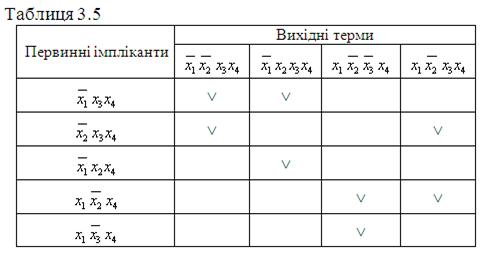
Після третього етапу в результаті викреслення стовпців 2, 3, 7 і 8 одержуємо таблицю 3.5. Якщо в таблиці є два стовпці, в яких є позначки в однакових рядках, то один з них викреслюється. Покриття стовпця, що залишився, буде здійснювати відкинутий мінтерм. В прикладі такого випадку немає.

Етап 5. Викреслення зайвих первинних імплікант.

Якщо після викреслення декількох стовпців на етапі 4 в табл. 3.5 з’являються рядки, в яких немає жодної позначки, то первинні імліканти, які відповідають цим рядкам, виключаються з подальшого розгляду, оскільки вони не покривають мінтерми, що залишилися.

Етап 6. Вибір мінімального покриття.

Вибирається в таблиці 3.5 така сукупність первинних імплікант, яка містить позначки в усіх стовпцях. При декількох можливих варіантах такого вибору надається перевага варіанту покриття з мінімальним сумарним числом букв в імплікантах, що створюють покриття. Цю вимогу задовольняють первинні імпліканти і .

Таким чином, мінімальна форма заданої функції буде складатися з суми суттєвих імплікант і первинних імплікант, які покривають мінтерми, що залишились:

          .

Нижче наведено таблиці (3.2-3.5), в яких поданий даний приклад.