3.2.     Метод Квайна-Мак-Класкі

В методі Квайна-Мак-Класкі використовується геометричне подання логічних функцій.

Якщо функція містить два аргументи, то їй відповідають набори 00, 01, 10, 11 (рис. 3.1, а). В декартових координатах візьмемо дві осі х₁, х₂. В точці перетину координат х₁=0, х₂=0 відкладаємо одиничні відрізки на осях х₁ і х₂.

    

    

б)

Перетин координат з точками 01 і 10 дає значення аргументів функції 11; можна використовувати тривимірний простір (куб) при поданні функції 3-х аргументів (рис. 3.1, б).

В загальному випадку функції алгебри логіки, які мають n аргументів, зображуються n-вимірним кубом.

Недоліком методу Квайна є необхідність повного попарного порівняння всіх мінтермів на етапі знаходження первинних імплікант. Із збільшенням кількості мінтермів збільшується кількість попарних порівнянь. Числове подання функції алгебри логіки дозволяє спростити етап знаходження первинних імплікант. Всі мінтерми записуються у вигляді двійкових номерів, а всі номери розбиваються за кількістю одиниць на групи, що не перетинаються, оскільки умовою утворення r-кубу є наявність розбіжності в (r-1) кубах лише за однією координатою (в одному двійковому розряді) та наявність загальних незалежних координат. Тому групи, які відрізняються в двох розрядах або більше, просто немає сенсу порівнювати. При цьому в і-ту групу ввійдуть всі номери (набори), що мають у своєму двійковому записі і одиниць. Попарне порівняння можна проводити лише між сусідніми за номерами групами.

Нехай задано функцію:

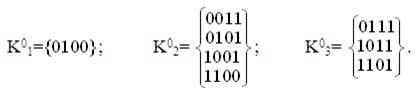
Розглянемо її мінімізацію за методом Квайна-Мак-Класкі:

Спочатку випишемо 0-куби:

К⁰={0011,0100,0101,0111,1001,1011,1100,1101}.

Розіб’ємо 0-куби на три групи за кількістю одиниць в кожному двійковому наборі:

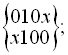
За методом Квайна-Мак-Класкі мінімізація логічної функції буде складатися з таких етапів:

Етап 1. Знаходження первинних імплікант.

а) порівняння K⁰₁ та K⁰₂ :

    

На основі порівняння будуємо куб K¹₁, в якому поглинену координату замінюємо символом х:

K¹₁=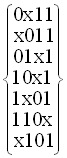

б) порівняння K⁰₂ та K⁰₃ :

    

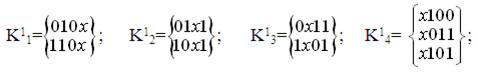
На основі порівняння будуємо куб K¹₂, в якому поглинену координату замінюємо символом х:

K¹₂=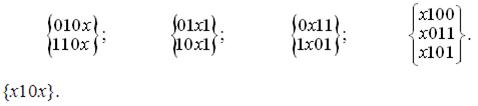

Первинних імплікант рангу 4 немає.

в) розіб’ємо всі 1-куби на чотири групи залежно від положення незалежної координати х:

г) на основі порівняння всередині кожної групи K¹₁ , K¹₂ ,K¹₃ та K¹₄ отримаємо результати:

Отже первинні імпліканти рангу 3:

.

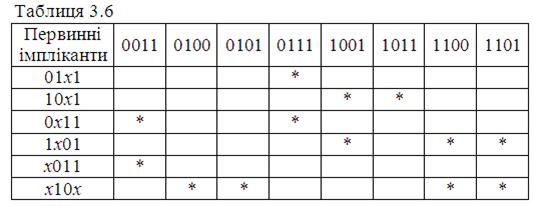Відповідно одержуємо первинну імпліканту рангу 2:

.

Етап 2. Встановлення позначок.

В таблицях (3.6-3.7) подані результати мінімізації заданої функції за методом Квайна-Мак-Класкі.

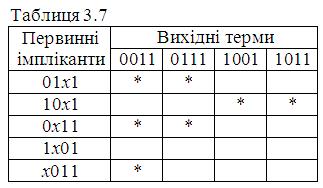
Етап 3. Знаходження суттєвих імплікант.

Суттєвою імплікантою рангу 2 будемо називати терм

{х10х} = .

Етапи 4 і 5. Відсутні.

Етап 6. Вибирається мінімальне покриття термів, що залишилися {10х1} і {0х11} (табл. 3.5)

Результат: