3.8 Мінімізація не повністю визначених функцій алгебри логіки
Не повністю визначена логічна функція n змінних – це функція, задана на числі наборів, менших 2n, тобто це логічні функції fi, які задані не на всіх 2n наборах аргументів х1, х2, … , хn
Приклад:
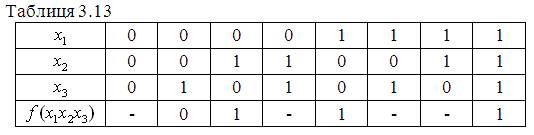
Вихідна функція 
: 
.
Довизначимо функцію 
одиницями і запишемо функцію 
:
.
Методом діаграм Вейча приведемо f1 до скороченої форми: використання діаграм Вейча для функції з трьома аргументами:
.
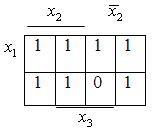
За допомогою метода Квайна побудуємо імплікантну таблицю:
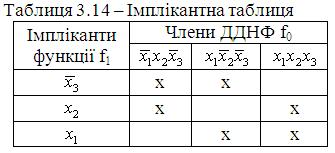
Мінімальна форма може бути отримана шляхом вилучення будь-якої з 3-х простих імплікант.
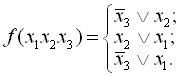
Розглянемо мінімізацію тієї ж функції діаграмою Вейча.
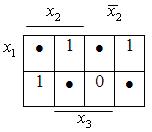
· - заборонений набір.
Необхідно на заборонених наборах аргументів надавати функціям такі значення, при яких клітинки із значенням 1 охоплюються мінімальною кількістю областей з максимальною кількістю клітинок в кожній з областей. У цьому випадку до визначення функції може бути виконано трьома різними способами:
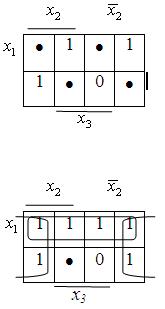
Дві області по 4 одиниці 
.
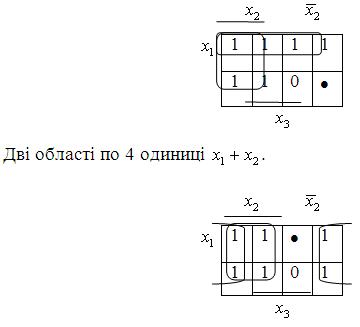
Дві області по 4 одиниці 
.