3.9     Мінімізація систем булевих функцій

На практиці часто необхідно реалізовувати сукупності булевих функцій. Якщо зробити мінімізацію булевих функцій, які входять в систему незалежно одна від одної, то загальна схема буде складатися з ізольованих підсхем. Для того, щоб спростити отриману схему, використовують метод мінімізації булевих функцій, який грунтується на методі Квайна.

Нехай задано систему повністю визначених булевих функцій, які подані в ДНФ:

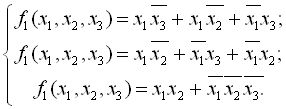
Всі різні елементарні кон’юнкції системи об’єднуємо в множину А, яку назвемо повною множиною елементарних кон’юнкцій системи функцій.

Сума рангів (число букв) елементарних кон’юнкцій множини А є зручним критерієм для оцінювання складності заданої системи.

Означення. Система ДНФ булевих функцій називається мінімальною, якщо її повна множина елементарних кон’юнкцій має мінімальну кількість букв, а кожна ДНФ булевої функції системи містить мінімальне число елементарних кон’юнкцій найбільшого рангу.

Алгоритм мінімізації систем булевих функцій

1. Побудувати повну множину А елементарних кон’юнкцій системи, яку мінімізуємо, враховуючи, що спочатку кожна з функцій системи подана в ДДНФ. Кожній конституенті одиниці множини А присвоїти ознаку, що містить номери функцій системи, в яку входить розглядувана конституента.

2. Виконати мінімізацію ДДНФ функції , конституентами якої є всі елементи множини А. При цьому:

а) при склеюванні двох конституент одиниці кожній одержаній елементарній кон’юнкції присвоїти ознаку, що складається з номерів функцій, загальних для двох склеюваних конституент одиниці;

б) якщо ознаки не мають спільних номерів, то склеювання не відбувається;

в) поглинання відбувається тільки для елементарних кон’юнкцій з однаковими ознаками. Одержані в результаті склеювання і поглинання кон’юнкції називаються простими імплікантами системи функцій.

3. Побудувати таблицю імплікант функції , аналогічно до методу Квайна, тільки для кожної конституенти одиниці виділяється стільки стовпців, скільки різних номерів функцій має її ознака.

Приклад.

Система булевих функцій задана таблицею істинності.

Таблиця 3.15 – Таблиця істинності

Подамо кожну з функцій в ДДНФ:

1.     Побудуємо повну множину елементарних кон’юнкцій системи, яку отримали, приписуючи кожній конституенті ознаку входження до функцій і :

.

2.     Будуємо ДДНФ функції :

.

     1     2     3     4     5     6

Пронумеруємо конституенти для зручності склеювання.

1-2 :

2-3 :

4-6 :

5-6 :

Після проведення поглинань (), з урахуванням ознаки, маємо:

.

Таким чином отримано прості імпліканти вихідної системи булевих функцій

3.     Будуємо імплікантну матрицю. Стовпці – конституенти одиниці з ДДНФ фунції . Для кожної конституенти виділяємо стільки стовпців, скільки різних номерів функцій мають ознаку конституенти.

Рядки матриці – прості імпліканти системи.

Заповнення матриці аналогічно до методу Квайна. Отримане ядро покриває всі конституенти одиниці з ДДНФ функції .

Таблиця 3.16

.

Виділяємо для функції імпліканти з ознакою, що містить ознаку і, отримаємо таку мінімальну диз’юнктивну нормальну форму системи.

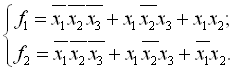
Недолік: велика громіздкість проведення операцій склеювання та поглинання з ознакою.