Додаток Б
Прикладна задача теорії графів
Методи теорії графів дозволяють розв’язувати багато технічних та теоретичних задач, таких як розрахунок електронних схем, задачі аналізу та синтезу кінцевих автоматів, задачі визначення потоків в мережах та інші.
Розглянемо задачу мінімального розфарбування графа, для розв’язання якої використаємо процедури мінімізації в алгебрі логіки.
Короткі відомості з теорії графів.
Вважають, що граф G = (X, U, F) заданий, якщо маємо X − множина вершин, U − множина ребер, F – тримісний предикат, який називають інцидентором, та який визначає, котрій парі вершин x,yÎX ставиться у відповідність ребро uÎU.
Граф можна задати графічно у вигляді рисунка та за допомогою матриць. Розглянемо приклад графа G(X, U), який зображений на рисунку 1, де X={x1, x2, x3, x4, x5} – множина вершин, U={u1, u2, u3, u4, u5} – множина ребер. Число вершин графа називається потужністю.
Матриця R = ||rij|| називається матрицею суміжності графа G = (X,U), якщо її елементи створюються за правилом: rij=1, якщо вершини xixj![]() X з'єднані з ребром U і rij=0, якщо вершини xixj
X з'єднані з ребром U і rij=0, якщо вершини xixj![]() X не суміжні.
X не суміжні.
Для графа G ( рис. 1) матриця суміжності має вигляд:
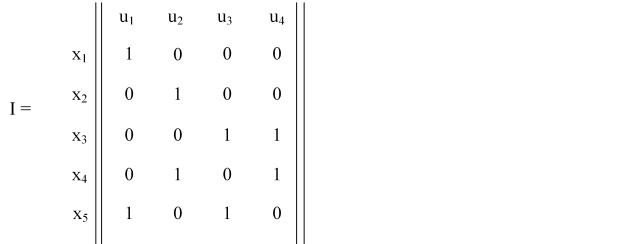
Рисунок 1 – Матриця суміжності графа
Матриця І = ||іkl||n×r, |x| = n (число вершин графа) |u| = r (число ребер графа), називається матрицею інцидентності графа G, якщо її елементи створюються за правилом: іkl=1, якщо вершини хk інцидентна ребру Ul і іkl=0 якщо хk не інцидентна ребру Ul
Для графа G ( рис.2 ) матриця інцидентності має вигляд:
![]()
Рисунок 2 – Матриця інцидентності графа
Дамо поняття розфарбування графа.
Граф G(X, U) називається k – хроматичним (k – розфарбування), якщо можна відмітити всі вершини Х графа G індексами 1, 2, … , k, тобто розфарбувати вершини k різними кольорами) так, щоб будь-які дві суміжні вершини були відмічені різними індексами. Хроматичне число графа k(G) визначається найменшим значенням k.
Зробимо індексацію вершин графа G1, зображеного на рис. 3.
Рисунок 3 – Граф G1
В даному випадку використано мінімальну кількість фарб – дві, тобто хроматичне число дорівнює k(G) = 2.
Підмножина вершин графа ![]() називається внутрішньо стійкою, якщо будь-які дві вершини з цієї підмножини не суміжні. В кожному графі G можна виділити сім’ю
Ψ={Ψ1
,Ψ2
…
Ψl} всіх внутрішньо стійких підмножин. Число внутрішньої стійкості
ŋ(G) визначається потужністю внутрішньо стійкої підмножини, яка має найбільшу кількість елементів.
називається внутрішньо стійкою, якщо будь-які дві вершини з цієї підмножини не суміжні. В кожному графі G можна виділити сім’ю
Ψ={Ψ1
,Ψ2
…
Ψl} всіх внутрішньо стійких підмножин. Число внутрішньої стійкості
ŋ(G) визначається потужністю внутрішньо стійкої підмножини, яка має найбільшу кількість елементів.
Для графа на рис. 3 будемо мати сім’ю внутрішньо стійких підмножин Ψ={ Ψ1 ,Ψ2}, де Ψ1={ x1 , x3} , Ψ2={ x2}, отже ŋ(G) = 2.
Розв’язання задач розфарбування графа з використанням методів булевої алгебри
Розфарбування графа здійснимо за допомогою алгоритму Х. Магу, Дж.Уесмана [14]. За цим алгоритмом на основі матриці інцидентності графа складається добуток:
,
де l – множник добутка є сумою 2-х доданків, які відповідають двом вершинам графі, які з’єднані k-м ребром.
Підмножина вершин
![]() є внутрішньо
стійкою, якщо ДG=1 для
системи змінних
є внутрішньо
стійкою, якщо ДG=1 для
системи змінних
![]() ,
які визначаються таким чином:
xi'=1,
якщо xi
,
які визначаються таким чином:
xi'=1,
якщо xi
![]() ψi і
xi'=0
якщо xi
ψi і
xi'=0
якщо xi
![]() ψi.
ψi.
Для отримання мінімальної форми виразу для ДG використаємо такі закони булевої алгебри: дистрибутивний, асоціативний та комутативний закони, а також співвідношення ![]() та закон поглинання. Тоді всі доданки цієї суми як множники будуть мати вершини з Х\
та закон поглинання. Тоді всі доданки цієї суми як множники будуть мати вершини з Х\![]() (тільки тоді ДG =1)
(тільки тоді ДG =1)
Приклад: Розглянемо рішення задачі для графа G(X,U) на рис. 1. Використовуючи матрицю інцидентності складаємо вираз для ДG :
ДG=(х1+ х5)( х2+ х4)( х3+ х4)( х3+ х5).
Розкриваємо дужки і спрощуємо вираз за законами алгебри логіки:
ДG=(х1 ·х2+ х1·х4+ х2·х5+х4·х5)( х3+ х4·х5)= х1 ·х2 ·х3+ х1·х3·х4+ х2·х3·х5+х4·х5.
Отже отримаємо сім’ю Ψ ={ Ψ1,Ψ2 ,Ψ3 Ψ4}, де , Ψ1={ x1 , x2 ,x3}
Ψ2={ x1 , x4}, Ψ3={ x4 , x5}, Ψ4={ x2 , x5} .
Для знаходження мінімального розфарбовування множини вершин графа виконаємо такі дії [14]. Будуємо матрицю А=||аij||, рядки (і) якої відповідають вершинам графа Хі, а стовпці (j)
– внутрішньо стійким підмножинам
ψi . На перетині і-го рядка і j-го стовпця ставиться 1, якщо xi
ψj , 0 – якщо xi![]() i . Для графа на рис. 1, матриця А має вигляд:
i . Для графа на рис. 1, матриця А має вигляд:
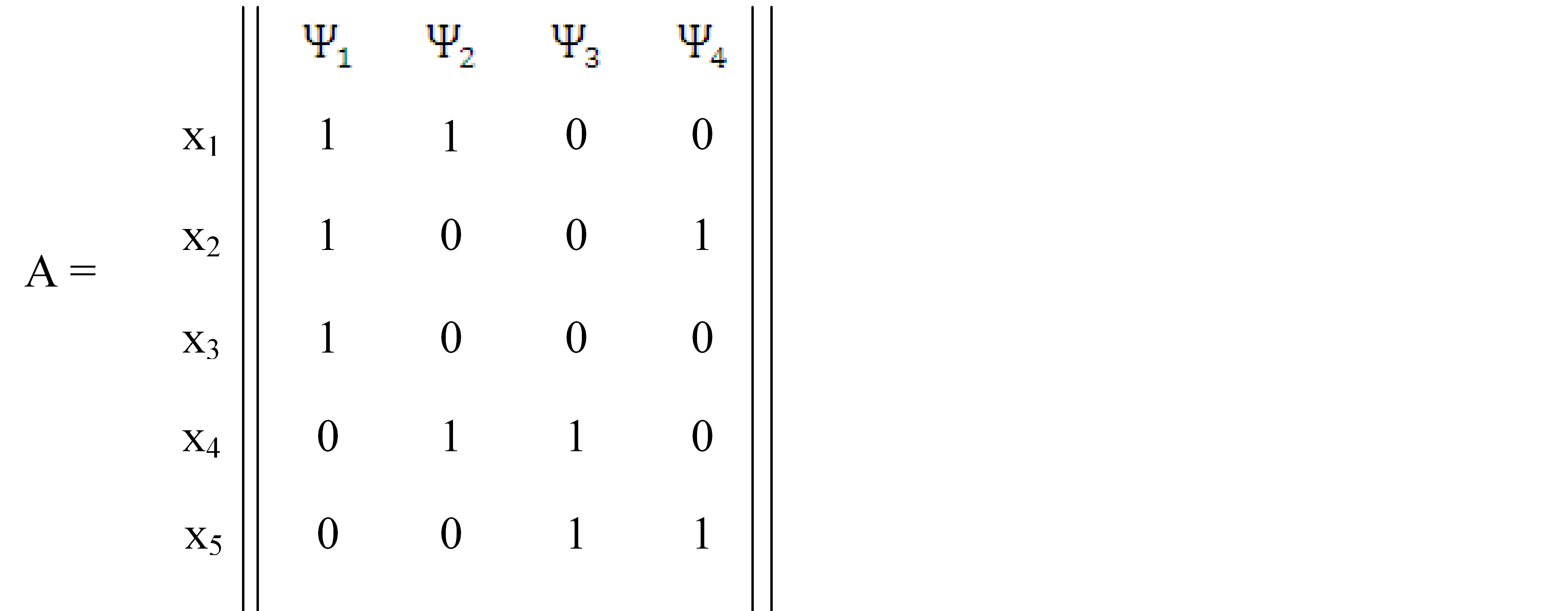
Після побудови матриці А кожній з вершин графа G співвідносять суму тих , які містять цю вершину, і записують добуток цих сум. Отже будемо мати такий вираз:
Д′G=(Ψ1 + Ψ2) (Ψ1 + Ψ4) (Ψ2 +Ψ3) (Ψ3 + Ψ4)Ψ 1
У виразі Д′G розкриваємо дужки та спрощуємо вираз за правилами булевої алгебри. Після мінімізації виразу будемо мати:
Д′G=(Ψ1 + Ψ1Ψ2Ψ4) (Ψ3 + Ψ2 Ψ4) = Ψ1Ψ3+Ψ1Ψ2Ψ4.
Кожний додаток Д′G має підмножини, які містять в неявному вигляді всі вершини графа G. Для знаходження всіх можливих мінімальних розфарбувань треба розписати доданки і скасувати вершини, які дублюються в найменшому з додатків. Отже для графа G на рис.1 мінімальна кількість фарб є дві, які визначаються внутрішньо стійкими підмножинами Ψ1 та Ψ3; тобто, наприклад, вершини {x1, x2, x3} пофарбуємо в білий колір, а вершини{x4, x5} – в червоний.