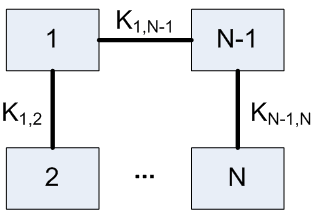
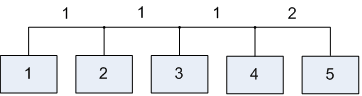
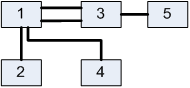
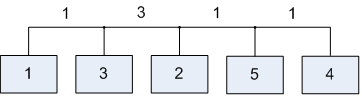
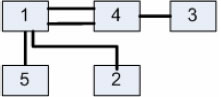
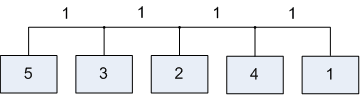
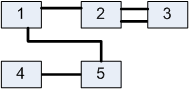
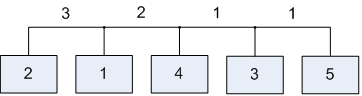
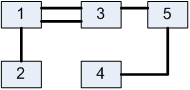
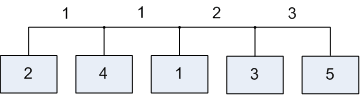
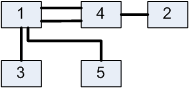
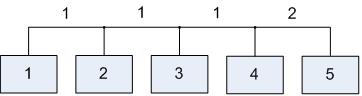
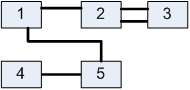
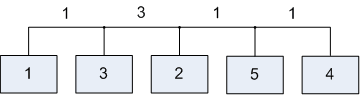
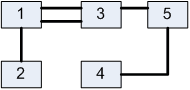
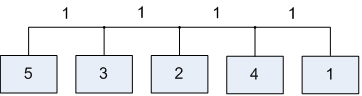
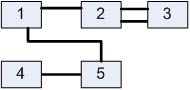
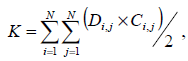Метод зворотного розміщення елементів

Мета: ознайомитись з методом зворотного розміщення елементів та набути практичних навичок використання.

1.1 Основні теоретичні відомості

Мета алгоритму полягає у розміщенні в дискретному координатному просторі елементів таким чином, щоб забезпечити максимальний критерій якості.

Завдання зводиться до знаходження таких позицій, у яких оптимізовано обраний показник якості і забезпечено найкращі умови для подальшого електричного монтажу.

Для оцінювання якості розміщення елементів використовують критерії, що безпосередньо пов'язані з отриманням оптимального рисунка металізації друкованої плати. Результат оптимізації на етапі розміщення знаходиться після вирішення задач розміщення і трасування комплексно, що неможливо внаслідок великих затрат. Тому алгоритми, що застосовуються для розміщення використовують проміжні критерії, які лише якісно сприяють вирішенню основної мети: отримання оптимального трасування між компонентами. До таких критеріїв відносяться.

1. Мінімальна сумарна довжина провідників.

2. Мінімальна довжина окремого провідника.

3. Максимальна щільність розміщення елементів на платі.

Найбільшого поширення в алгоритмах розміщення отримав перший критерій, який зменшує довжину зв'язків, і покращує електричні характеристики пристрою, спрощує трасування друкованих плат і є порівняно простим в реалізації.

Для роботи алгоритму буде використано схему місць, подану на рис. 1.1 і схему з'єднань подану на рис. 1.2.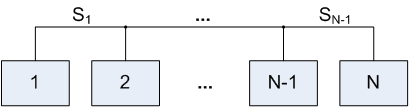

Відповідно до поданої на рис. 1.1 схеми необхідно створити матрицю відстаней. Матриця відстаней являє собою квадратну матрицю з розмірністю, що відповідають загальній кількості елементів схеми та нульовою діагоналлю. Елементи матриці дорівнюють сумарній кількості з'єднань між елементами. Відстані розраховано за формулою (1.1).

(1.1)

де D_i,"j – значення елементу матриці відстаней;

i, j – індекси стовпця і рядка, відповідно;

S_i,"j – довжини зв'язків між елементами.

Розрахунок елементів вектора-стовпця, що характеризує сумарну довжину зв'язків між елементом вектора-стовпця і іншими елементами схеми місць виконується за формулою (1.2)

(1.2)

де D*_j – значення елементу вектора;

D_i,"j – значення елементу матриці відстаней;

i, j – індекси стовпця і рядка.

Відповідно до поданої на рис. 1.2 схеми сформовано матрицю зв'язків, що являє собою квадратну матрицю з нульовою діагоналлю. Елементи матриці дорівнюють сумі безпосередніх з'єднань між елементами. Кількість зв'язків між елементами розраховано за формулою (1.3).

(1.3)

де C_i,"j – значення елементу матриці зв'язків;

i, j – індекси стовпця і рядка, відповідно;

K _i,"j – кількість зв'язків між елементами.

Розрахунок елементів вектора-стовпця, що враховує сумарну кількість зв'язків для кожного елементу схеми виконується за формулою (1.4).

(1.4)

де С*_j – значення елементу вектора;

С_i,"j – значення елементу матриці зв'язків;

i, j – індекси стовпця і рядка.

Розміщення найбільш завантажених елементів виконується у найменш віддалених місцях таким чином, щоб такі елементи вектора сум зв'язків розташувати у найменш віддалених (найменша довжина зв'язків) місцях відповідно до вектора сум відстаней, корегуючи схему місць елементів подану на рис. 1.1, відповідно (1.5), (1.6)

(1.5)

(1.6)

Недоліком алгоритму є те, що він не забезпечує оптимального варіанта, але дає можливість на 10-20% зменшити сумарну довжину провідників. Цей алгоритм може бути використано для початкового розміщення елементів.

Для оцінювання ефективності розміщення використано сумарну довжину провідників, що обчислена як половина суми добутків кожного елементу матриці С на відповідний елемент матриці D.

(1.7)

де С– матриця зв'язків;

D – матриця відстаней;

i, j – індекси стовпця і рядка.

1.2 Порядок виконання роботи

1. Відповідно до схеми місць елементів створити матрицю відстаней.

2. Розрахувати вектор-стовпець відповідно до матриці відстаней.

3. Створити матрицю зв'язків відповідно до поданої схеми з'єднань елементів.

4. Розрахувати вектор-стовпець відповідно до матриці зв'язків.

5. Провести розміщення найбільш завантажених елементів у найменш віддалених місцях таким чином, щоб найбільш завантажені елементи вектора сум зв'язків розташувати у місцях найменш віддалених відповідно до вектора сум відстаней, корегуючи схему місць елементів.

6. Визначити критерії якості.

7. Порівняти значення критеріїв якості початкової і оптимізованої схеми, зробити висновки.

1.3 Зміст звіту

1. Мета та цілі роботи.

2. Розрахункова частина. (Основні розрахункові формули та розрахунок)

3. Програма, написана мовою програмування (C++, C# , Pascal), що виконує задачу поставлену у лабораторній роботі.

4. Висновки.

1.4 Контрольні запитання

1. Принципи роботи алгоритму розміщювання.

2. Які критерії використовуються для оцінювання якості розміщення елементів?

3. Як формуються матриця і вектор довжин зв'язків?

4. Як формуються матриця і вектор кількості зв'язків?

5. Як проводиться оптимізація використовуючи вектори сум довжин і кількості зв'язків?

6. Замініть позиції 1 та 3 елементів і сформуйте матриці довжин і кількості зв'язків між елементами схеми розміщення.

7. Замініть кількість зв'язків між 2 та 5 елементів і сформуйте матриці довжин і кількості зв'язків між елементами схеми розміщення.

1.5 Варіанти завдань

Номер	Схема місць	Схема з'єднань
1
2
3
4
5
6
7
8