Отрезки прямых в совокупности графических примитивов имеют наибольший удельный вес. В связи с этим при разработке графических продуктов алгоритмам линейной интерполяции уделяют особое внимание, поскольку производительность системы во многом зависит от скорости формирования отрезков прямых.

При выборе алгоритма основными критериями есть быстродействие формирования шаговой траектории, погрешность интерполирования, вычислительная сложность, метод реализации (программный, аппаратный, программно-аппаратный).

Среди способов задания отрезков прямых в машинной графике наибольшее распространение получили следующие:

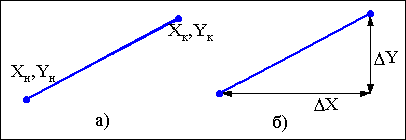
*  координатами начальной и конечной точки (рис.1.1а) ;

*  приращениями координат (рис.1.1б).

Рис. 1.1. Способы задания отрезков прямых

Во втором способе вектор задается начальной точкой и приращениями DХ и DY отрезка прямой, которые определяют конечную точку.

В зависимости от типа формируемых элементарных шаговых перемещений на дискретной прямоугольной сетке различают алгоритмы с четырех и восьми векторным направлением шаговых приращений. Во-первых, в алгоритмах используют раздельные шаги по ведомой и ведущей координатах, а во-вторых – еще и совмещенные (диагональные) шаги. Алгоритмы с четырех векторным направлением шаговых приращений обеспечивают погрешность интерполирования отрезка не превышающую шага дискретизации, а с восьми векторным направлением – вдвое меньшую.

Большинство методов линейного интерполирования ориентированы для формирования траектории в одном из квадрантов прямоугольной системы координат. При формировании траектории в любом квадранте используют специальные приемы переключения знаков переменных.

Линейное интерполирование содержит два этапа: цикл подготовки и цикл интерполирования. В цикле подготовки, как правило, определяют октант формирования отрезка прямой, ориентацию по отношению к координатным осям, а также выполняют необходимые предварительные расчеты. В цикле интерполирования по алгоритмическим зависимостям находят значения шаговых приращений, осуществляют их выдачу и анализируют окончание формирования траектории.

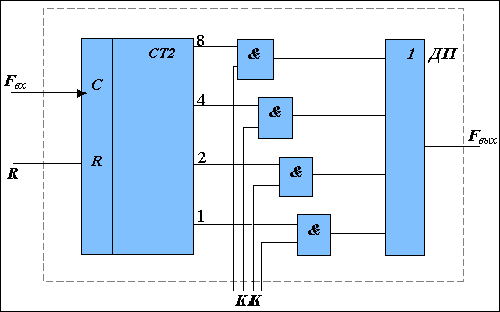
Рис. 1.2. Функциональная схема двоичного умножителя

Среди методов формирования отрезков прямых наибольшее распространение получили «прямой» метод, метод цифрового дифференциального анализатора (ЦДА), метод оценочной функции. При реализации “прямого” метода координаты точек траектории находят в соответствии с известным уравнением прямой:

При DХ³DY в приведенное уравнение подставляют текущую координату Х и находят координату Y, а при DХ<DY – наоборот. Погрешность интерполяции при реализации метода определяется выбранным способом округления.

Необходимость выполнения “длинных” операций существенно ограничивает применение метода, поскольку реализация операции деления требует значительных временных затрат вследствии заменны деления при использовании программных средств другими действиями.

При использовании метода ЦДА отношение Р=DY/DХ находят в цикле подготовки, а операцию умножения на Х заменяют накапливающим суммированием. Очевидно, что при DХ³DY значение Р£0. Если при накапливающем суммировании операнда DY/DХ имеет место сигнал переполнения для целой части числа, то текущее значение Y увеличивают на единицу. Текущее значение Х увеличивают на единицу в каждом такте.

При DХ<DY находят отношение DХ/DY и выполняют перечисленные выше действия, но уже со сменой координат.

В методе цифрового дифференциального анализатора широко используются также двоичный умножитель (интегратор последовательного переноса), название которого определяется выполнением последним функции вида:

где УК – значение управляющего кода, n – разрядность умножителя, f_вх, f_вых – значение соответственно входной и выходной частоты опорной импульсной последовательности.

Упрощенная функциональная схема двоичного умножителя приведена на рис.1.2. Двоичный умножитель ДУ обеспечивает преобразование управляющего кода УК в количество импульсов, которые формируются на его выходе за Т=2ⁿ тактов счета.

Двоичный умножитель включает двоичный счетчик СТ2 и логическую схему, в состав которой входят элементы И и элемент ИЛИ. За цикл перерасчета счетчика СТ2 на его выходах будут сформированы импульсные последовательности (рис.1.3), количество импульсов в которых равно степеням двоек (образовывают двоичные разряды).

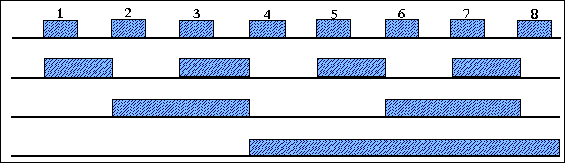
Рис. 1.3. Временная диаграмма работы трехразрядного двоичного счетчика.

Единичные значения разрядов управляющего кода УК разрешают роботу соответствующих элементов И, что предопределяет прохождение на их выход импульсных последовательностей, которые генерируются на выходах счетчика. Элемент ИЛИ обеспечивает объединение импульсных последовательностей в выходной поток F_вых за Т=2ⁿ тактов на выходе двоичного умножителя будут сформированы УК импульсов.

В алгоритме используется вспомогательная переменная – время Т, которое определяется циклом пересчета счетчика СТ2. Поскольку реализуется уравнение прямой, заданной в параметрической форме, то линейные интерполяторы такого класса часто называют параметрическими.

Структурная схема параметрического линейного интерполятора приведена на рис.1.4.

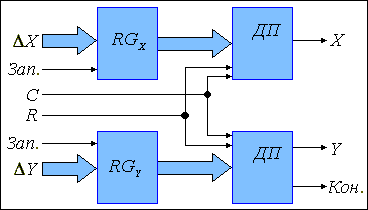
Рис. 1.4. Структурная схема параметрического линейного интерполятора.

Интерполятор включает два регистра для хранения приращений заданного вектора, которые образуют управляющие коды для ДУ, а также два двоичных умножителя. Последние за 2ⁿ тактов формируют на своих выходах количество импульсов, которые равны исходным приращениям.

На рис.1.5 приведен пример формирования параметрическим линейным интерполятором отрезка прямой с DХ=5, DY=3.

Один из существенных недостатков приведенного параметрического линейного интерполятора состоит в том, что он формирует отрезки прямой, независимо от их длины, за 2ⁿ тактов. Время интерполирования можно уменьшить за счет нормализации – одновременного увеличения исходных приращений в заданное число раз. При этом цикл интерполирования уменьшают в столько же раз.

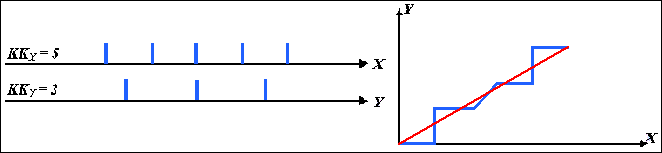
Рис. 1.5. Пример формирования отрезка прямой параметрическим линейным интерполятором.

Приведенный подход ориентирован на аппаратную реализацию, имеет достаточно высокое быстродействие, но сформированные траектории имеют плохую гладкость за счет возможного формирования горизонтальных, вертикальных и диагональных шагов. Погрешность интерполирования определяется неравномерностью поступления импульсов на выход ДУ, дискретным характером формирования траектории и пропорциональна разрядности интерполятора.

Согласно алгоритма симметричного интегратора вычисление интеграла выполняется приближенно, путем суммирования (например по методу Эйлера). При этом вычисляют:

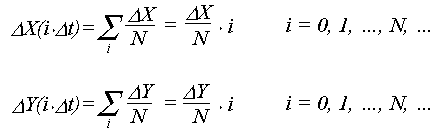
Значение N должно быть выбрано таким образом, чтобы шаги по DХ(iDt) и DY(iDt) были меньше размера пятна, поскольку только в этом случае вектор будет выглядеть как сплошная линия. Данное условие выполняется, если размер шага меньше одной единицы растра. Отсюда можно получить условие для определения N: DХ/N<1 и DY/N<1, или N>max(|DX|, |DY|).

Недостаток приведенного алгоритма состоит в том, что приращения DX, DY необходимо делить на N. Деление можно заменить сдвигом, если принять величину N равной одной из степеней двойки. В этом случае получаем условие:

N = log₂ max(½DX½,½DY½)

На практике в преобладающем большинстве случаев для линейного интерполирования используют метод оценочной функции. Указанное обусловлено высокой точностью интерполирования, простотой программной и аппаратной реализации и относительно высоким быстродействием, определяемым временем выполнения микрооперации суммирования.  

Общим приемом для всех интерполяторов, которые работают по методу оценочной функции, есть анализ знаков оценочной функции, на основе которых делают шаг по той или иной координате с дальнейшим расчетом ее нового значения и коррекцией соответствующей координаты текущей точки.

Пусть необходимо сформировать отрезок прямой, который задан приращениями Dx и Dy по осям координат (см.рис.1.6).

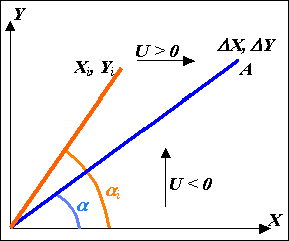
Рис. 1.6. Формирование оценочной функции.

Если точка траектории находится выше прямой ОА, то оценочная функция U>0 и следующий шаг необходимо выполнять по оси X; если точка находится ниже этой прямой, то U<0 и следующий шаг необходимо выполнять по оси Y. Таким требованиям отвечает функция вида:

U_i = tga_i – tga

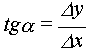
где x_i, y_i – текущие координаты формируемей траектории.

Тогда

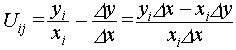
Поскольку произведение x_iDx – положительно и не влияет на знак U_ij, знаменателем дроби можно пренебречь. Таким образом,

U_ij = y_iDx – x_iDy              (1)

Определим новое значение оценочной функции при выполнении шага по оси X. В этом случае x_i+1=x_i+1. После подстановки в (1) значение для x_i+1, получим

U_i+1,j = y_iDx – Dy(x_i+1) = y_iDx – x_iDy – Dy = U_ij – Dy

После шага по оси y при U<0 получаем новое значение y_i+1=y+1. Тогда новое значение оценочной функции

U_i,j+1 = Dx(y_i+1) – Dyx_i = y_iDx + Dx – x_iDy = U_ij + Dx

Приведенный алгоритм имеет четырех векторную ориентацию шаговых приращений и обеспечивает погрешность, не превышающую шага интерполирования.

Погрешность интерполирования можно уменьшить, если использовать диагональные шаговые приращения. Такой тип приращения рассматривают как одновременное горизонтальное и вертикальное перемещения. Учитывая вышеуказанное, после такого шага новое значение оценочной функции определяется как U_i+1,,j+1=U_i +Dx–Dу.

Ненулевое начальное значение оценочной функции позволяет отсимметрировать погрешность интерполирования, что уменьшает ее вдвое. На рис.1.7а приведена неотсимметрированная шаговая траектория. За счет размещения диагонального шагового приращения посредине цифрового сегмента погрешность интерполирования d₁^– заменяется на две: d⁺ и d^– (см.рис.1.7б), что значительно меньше исходной.

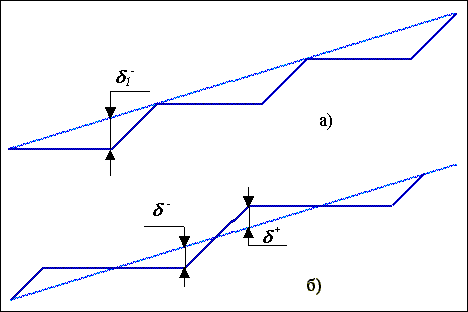
Рис.1.7. Уменьшение погрешности интерполирования за счет симметрирования.

Из формулы (1) видно, что значение оценочной функции определяет погрешность интерполирования. Указанное используется в алгоритме Томсона, согласно которого определяются оценочные функции для двух возможных шаговых перемещений. Соответствующей действительности шаг выполняется в том направлении, где значения оценивающей функции меньше.

Алгоритм Томпсона обеспечивает максимальную точность интерполирования, но требует определение сразу двух оценочных функций, что в свою очередь сказывается на его вычислительной сложности.

В соответствии с известным алгоритмом Брезенхема значения шаговых приращений определяются по знаку оценочной функции, которую рассчитывают согласно выражений:

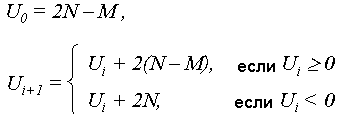
где N, M – соответственно большее и меньшее значения приращений отрезка.

Цикл интерполирования заканчивается после выдачи M шаговых приращений. Если U_i<0, то выполняется шаг по ведущей координате, а при U_i³0 – комбинированный шаг по обеим координатам. Алгоритм Брезенхема обеспечивает минимальную погрешность интерполирования, равную половине шага дискретизации, но требует увеличение исходных операндов вдвое. Это в ряде случаев может привести к необходимости работы со словами, которые превышают разрядную сетку процессора. Этот недостаток ликвидирован в алгоритме Петуха А.М., Ободника Д.Т. (Украина).

Значения оценочной функции в этом случае рассчитываются в соответствии с формулами:

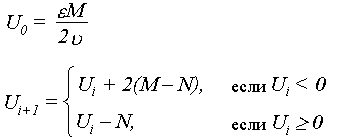
Если U_i³0, то выполняется шаговое перемещение по ведущей координате. В противном случае выполняется диагональное перемещение. Алгоритм обеспечивает максимальную точность. Анализ окончания интерполирования не отличается от указанной процедуры алгоритма Брезенхема.

Интерполирующие устройства формируют адреса точек траектории в дискретном координатном пространстве. На рис.1.8 приведена функциональная схема подключения интерполятора (программно или аппаратно реализованного).

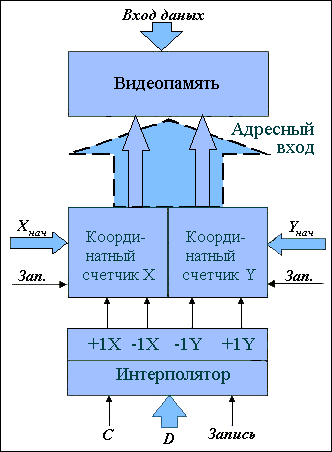
Рис. 1.8. Функциональная схема подключения интерполятора.

Адреса точек траектории формируют два координатных счетчика. Координаты начальной точки Х_нач, У_нач заносятся в соответствующие координатные счетчики в цикле подготовки и определяет их исходное состояние. Указанная микрооперация получила название позиционирования. При формировании интерполятором шаговой траектории, состояние координатных счетчиков изменяется инкрементно и определяет адрес ячейки видеопамяти. Для каждой точки траектории определяют код цвета, который выставляется на шину данных видеопамяти. Для некоторых режимов запись в видеопамять блокируется.