|
1. Методы и алгоритмы формирования контурных изображений |
|
1.3. Методы и алгоритмы формирования кривых второго порядка |
|
1.3.1. Окружность |
Дуги
окружностей,
как и
отрезки
прямых,
относят к
наиболее
распространенным
графическим
примитивам.
Существует
несколько
методов
задания
исходных
данных для
кругового
интерполирования.
X = XC + R× cosQ
Y = YC + R× sinQ
где Xc,Yc – координаты центра окружности, R – радиус окружности, Q – полярный угол.
Наиболее
часто
указывают
направление
движения (за
или против
часовой
стрелки),
приращения
координат
начальной и
конечной
точки дуги
окружности
относительно
его центра, а
также
координаты
начальной
точки дуги в
экранной
системе
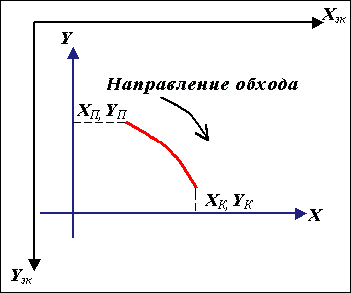
координат (рис.1.9).

Рис. 1.9. Задание дуги окружности.
При реализации кругового интерполирования необходимо учитывать:
* окружность это симметричная фигура, что позволяет существенно сократить время вычислений, поскольку для получения всех точек окружности достаточно сформировать их лишь для одного октанта;
* необходимо
проводить
анализ
перехода
через
границы
октантов,
поскольку
при этом
изменяется
направление
шаговых
приращений (см.рис.1.10).
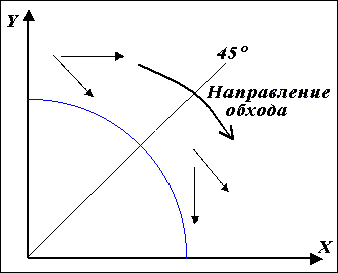
Рис.
1.10. Типы
шаговых
приращений
За счет погрешности интерполирования, а также округлений при определении начальной и конечной точек дуги существует вероятность не попадания в конечную точку дуги, что обусловливает необходимость введения в вычислительный процесс режима доводки в конечную точку.
Рассмотрим процедуру формирования окружности в полярной системе координат. Поскольку для вычисления координат точек окружности X, Y необходимо задавать дискретные значения полярного угла, то возникает проблема рационального выбора шага приращения этого угла – DQ. При малом шаге время построения окружности увеличивается, но обеспечивается высокая точность воспроизведения окружности. При большом значении DQ качество воспроизведения ухудшается, но время построения уменьшается.
Исходя из дискретной структуры растра, можно утверждать, что минимальное расстояние между соседними точками окружности не может быть меньше чем 1. Следовательно, все точки окружности без пропусков будут воспроизведенные при условии, что шаг приращения полярного угла будет выбираться из условия:
![]()
Для
сокращения
времени
формирование
окружности
из
вычислительной
процедуры
желательно
исключить
громоздкое
вычисление
тригонометрических
функций cosQ
и
sinQ. Для
этого
вычислим
очередную i+1 точку
окружности
в виде:
Xi+1 = R×Cos(Q+DQ)
Yi+1 = R×Sin(Q+DQ)
После замены получим:
Xi+1 = Xc + (Xi – Xc)CosDQ – (Yi – Yc)SinDQ
Yi+1 = Yc + (Xi – Xc)SinDQ – (Yi – Yc)CosDQ
Полученные рекуррентные соотношения для данного подхода обеспечивают максимальную скорость вычислений, так как значения sinDQ и cosDQ рассчитываются только один раз.
Согласно
прямого
метода, координаты
точек
траектории дуги
определяются
с
использованием
выражения
вида:
Х2+Y2=R2,
где Х, Y – текущие точки окружности, а R – ее радиус.
При
Х³В
значение
абсциссы
последовательно
увеличивают
на единицу, а
ординату
вычисляют
по формуле
Y = Ö ( R2 – X2)
а при Х<Y
для
текущего Y вычисляют
значения
Y = Ö ( R2 – H2)
Погрешность
интерполирования
определяется
количеством
разрядов,
отведенных
для
вычисления,
а также
способом
округления.
Траекторию окружности можно сформировать путем ее представления совокупностью хорд. Погрешность интерполирования определяется количеством хорд, которые были взяты для аппроксимации.
Для
некоторых
применений
такой метод
приемлемый,
например,
при работе с
окружностями
в
трехмерной
среде.
Однако
окружности,
построенные
с помощью
хорд, не
является
достаточно
сглаженными.
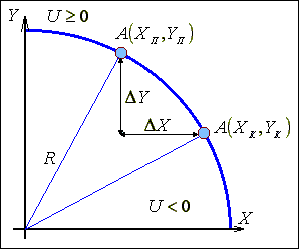
Рис.
1.11. Принцип
формирования
оценочной
функции.
Для реализации функции кругового интерполирования наиболее часто используют метод оценочной функции. Вид оценочной функции выбирают таким образом, чтобы внутри и за окружностью она имела противоположные знаки, а на самой окружности – нулевое значение. Таким требованиям отвечает функция вида:
Uij = X2 + Y2 – R2
При
U
Тогда
Ui+1,j = (Xi + 1)2 + Yi2 – R2 = Xi2 + Y i2 – R2 + 2Xi + 1 = Uij + 2Xi + 1
После
шага по оси Y
новое значение
оценочной
функции можно
определить
подставив в
формулу для Uij
вместо
Yi
величину
Yi+1=Yi–1.
Тогда значение оценочной функции после шага по оcи Y будет равно:
Ui+1,j = Xi + (Yi – 1) – R2 = Uij – 2Yi + 1
Таким образом, после шага по оси X к значению оценочной функции необходимо прибавить величину 2Xi+1, a после шага по ocи Y величину –2Yi+1. Таким образом, в любом случае прибавляется единица и прямой или дополнительный код величин 2Xi, 2Yi. После этого необходимо скорректировать значения Xi, Yi для получения Xi+1=Xi+1, Yi+1=Yi–1.
При
реализации
алгоритма с
восьмивекторной
ориентацией
шаговых
приращений
диагональный
шаг
формируют
путем
одновременного
элементарного
перемещения
по обеим
координатам.
В этом
случае
новое
значение
оценочной
функции
вычисляют
по формуле:
Ui+1,j = Uij + 2Xi + 1 – 2Yi + 1= Uij + 2(Xi – Yi) + 2
На
практике
широкое
распространение приобрел
алгоритм
кругового
интерполирования
сотрудника
фирмы ІВМ
Брезенхема.
При
формировании
окружности
во
втором
октанте в
направлении
часовой
стрелки
выполняются
следующие
действия:
Если U<0, то U:=U+4X+6, X:=X+1.
В противном случае U:=U+4(Xi–Yi)+10, X:=X+1, Y:=Y–1.
Указанные действия выполняют до достижения конечной точки октанта.
Приведенные
рекуррентные
выражения
для расчета
оценочной
функции
показывают,
что из
вычислительного
процесса
исключены “длинные”
операции,
что
обусловливает
высокую
производительность
метода, а
также
возможность
аппаратной
реализации.
Рассмотрим
режим
доводки в
конечную
точку дуги.
Для первого октанта
возможные
два случая,
которые
приведенные
на рис.1.12.
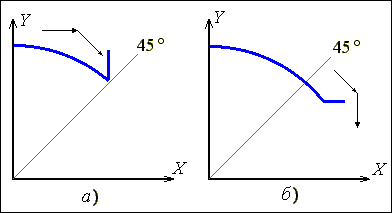
Рис.
1.12. Доводка в
конечную
точку дуги
Во
втором
октанте (рис.1.12а)
шаговая
траектория
формируется
горизонтальными
и
диагональными
(комбинированными)
шаговыми
приращениями.
Учитывая,
что
диагональное
приращение
включает
перемещение
по оси Х,
то
можно
констатировать,
что все
элементарные
шаги к точке Х=Y
включают
перемещения
по оси
абсцисс.
Отсюда
вытекает,
что при
формировании
траектории
гарантированно
будет
достигнута
координата Хк,
а доводка
будет
необходима
к
координате Yк.
Аналогично
можно
показать,
что при
формировании
дуги в
первом
октанте
доводке
подлежит
координата Хк.
|
Контрольные
вопросы. |
1.
Приведите характерные особенности кругового интерполирования.2. Какие формы
задачи дуг
окружностей
вам
известны?
3. Приведите сравнительную характеристику алгоритмов формирование окружностей.
4. Чем обусловленная необходимость доводки в конечную точку дуги?
5. Объясните, почему формулы для расчета точек траектории окружностей отличаются при разных направлениях обхода.