2. Процедуры машинной графики

2.1. Афинные преобразования

Аффинные преобразования находят широкое применение в задачах машинной графики. Наибольшего распространения приобрели частичные случаи аффинных преобразований: сдвиг, поворот, масштабирование.

Пусть на плоскости заданна начальная система координат 0ХY и некоторая новая система координат 0₁X₁Y₁. Тогда преобразование, которое состоит в том, что точке P плоскости ставится в соответствие точка P₁, которая в новой системе имеет такие же координаты, как и точка P в начальной, называются аффинными.

Основные свойства аффинных преобразований:

*  множество точек, которое в начальной системе координат удовлетворяет некоторому уравнению, переходит во множество точек, координаты которых в новой системе удовлетворяют такому же уравнению. При этом прямая переходит в прямую, плоскость в плоскость;

*  соотношение площадей и объемов геометрических фигур сохраняется;

*  сохраняется простое соотношение трех точек;

*  существует единственное преобразование плоскости, которое переводит тройку точек, которые не принадлежат одной прямой, в новую тройку точек, которые также не принадлежат прямой;

*  если начальная и новая системы координат есть декартовыми с одинаковыми единичными отрезками по осям, то при преобразованиях сохраняются все метрические свойства геометрических фигур.

На рис.2.1 изображены геометрические соотношения между начальной системой 0XY и системой 0X₁Y₁, которую получили при повороте начальной системы на угол a.

С помощью соотношений на рис.2.1 получаем систему уравнений 

что можно представить в матричном виде:

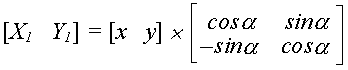
При повороте изображения не всегда получают целочисленные координаты, что приводит к необходимости их округления.

Функциональный метод поворота изображения исключает из вычислительного процесса выполнение синусно-косинусных преобразований и «длинных» операций.

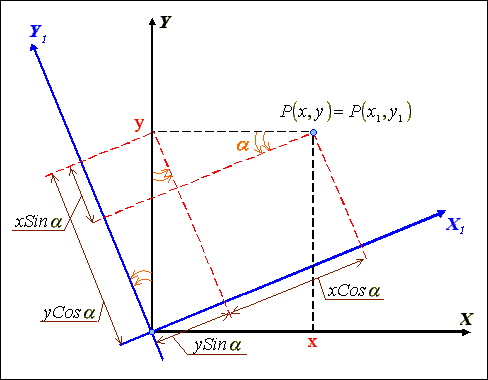
Рис. 2.1. Поворот системы координат

Сущность метода состоит в следующем.

Декартова плоскость 1  и соответствующая ей система координат ХОY образованна плоскостью экрана индикатора изображения, а декартова плоскость 2  и соответствующая ей система координат Х¹О¹Y¹ – плоскостью матрицы светочувствительных элементов (рис.2.2).

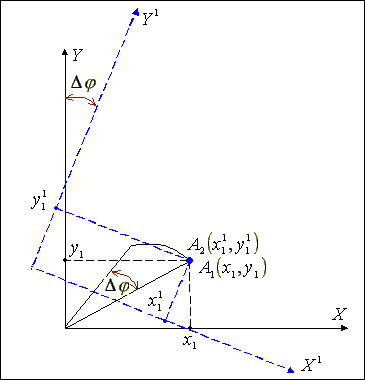
Рис. 2.2. Функциональний метод поворота

В начальный момент времени точка А1 с координатами Х1, Y1 отображается на экране индикатора. Матрица светочувствительных элементов, которая повернута по отношению к экрану на угол Dj, воспринимает точку в системе координат Х¹О¹Y¹, по отношению к которой последняя имеет координаты Х¹1, Y¹1. Очевидно, что отображая на экране точку с координатами Х¹1, Y¹1, осуществляется поворот исходной точки на угол Dj  в системе координат ХОY. Выполняя указанную процедуру для всех точек изображения, за время одного кадра осуществляется поворот изображения на угол Dj.

За счет повторения процесса n раз, где n=j/Dj, обеспечивается поворот изображения на заданный угол j.

Поскольку исходная и новая системы координат есть прямоугольными декартовыми с одинаковыми единичными отрезками по осям, то при преобразовании сохраняются все метрические свойства геометрических фигур.

Недостаток функционального метода поворота состоит в относительно большой погрешности преобразования.

При масштабировании осуществляют увеличение или уменьшение размеров изображение согласно с преобразованиями вида

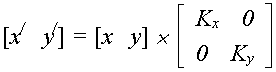
где K_x , K_y – масштабные коэффициенты.

При K_x=K_y=K осуществляется преобразование подобия. Изображение увеличивается в K раз при K>1 и уменьшается при K<1.

Точка сдвигается путем добавлением к каждой координате точки положительной или отрицательной константы:

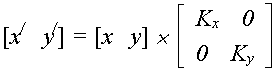
где m, n – значение параметров сдвига.

Контрольные  вопросы.

1.  Какие преобразования относят к аффинным?

2.  Какие основные свойства аффинных преобразований?

3.  Приведите формулы для поворота точки изображения на угол a против часовой стрелки.

4.  Возможное ли совмещение в одной процедуре различных типов аффинных преобразований?

5.  Как организуется скроллинг окна изображение?

     Содержание