1. Методи та алгоритми формування контурних зображень |
1.2. Методи та алгоритми формування векторів |
Відрізки прямих в совокупності графічних примітивів мають найбільшу питому вагу. В зв’язку з цим при розробці графічних пристроїв алгоритмам лінійної інтерполяції приділяють особливу увагу.
При
виборі алгоритму основними критеріями є
швидкодія формування крокової траєкторії,
похибка інтерполювання, обчислювальна
складність , тип формування крокової траєкторії (
програмний, апаратний, програмно-апаратний).
Серед
способів завдання відрізків прямих в машинній
графіці найбільшого поширення набули наступні:
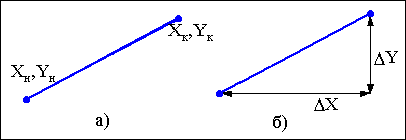
* координатами початкової та кінцевої точки (рис.1.1 ,а);
* приростами координат ( рис. 1.1,б).

Рис. 1.1. Способи завдання відрізків
прямих
В
другому способі вектор задається початковою
точкою та приростами ΔХ та ΔУ вектора, які
визначають кінцеву точку.
В залежності від типу формованих крокових переміщень на дискретній прямокутній сітці розрізняють алгоритми з чотирьох та восьмивекторною направленістю крокових приростів. В перших алгоритмах використовують спільні кроки по веденій та ведучій координатах, а в других спільні кроки. Алгоритми з чотирьохвекторною направленістю крокових приростів забезпечують похибку інтерполювання, яка не перевершує кроку дискретизації, а з восьмивекторною направленністю–вдвічі меншу.
Більшість
методів лінійного інтерполювання орієнтовано
для формування траєкторії в одному з квадрантів
прямокутної системи координат. При формуванні
траєкторії в будь-якому квадранті
використовують спеціальні прийоми переключення
знаків змінних.
Лінійне інтерполювання містить два етапи: цикл підготовки і цикл інтерполювання. У циклі підготовки визначають мажоритарність відрізка прямої, а також його орієнтацію по відношенню до координатних осей, що дозволяє встановити, в якому з октантів розміщено заданий відрізок прямої. У циклі інтерполювання за алгоритмічними залежностями знаходять значення крокових приростів, здійснюють їх видачу і аналізують закінчення формування траєкторії.
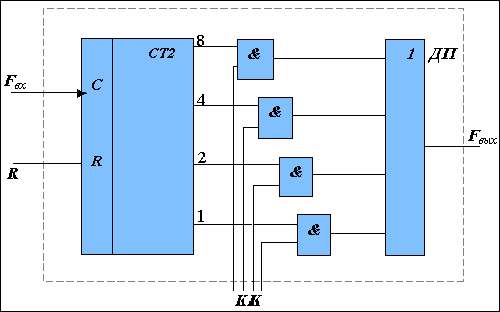
Рис. 1.2. Функціональна схема
двійкового помножувача
Серед методів формування відрізків прямих найбільшого поширення знайшли метод симетричного інтегратора, “прямий” метод, метод цифрового диференційного аналізатору, метод оцінювальної функції. Згідно “прямого” методу координати точок траєкторії знаходять з відомого рівняння прямої:
![]()
При ΔX≥ΔY в приведене рівняння підставляють поточну координату Х і знаходять координату Y, а при DХ<DY – навпаки. Погрішність інтерполяції при реалізації методу визначається обраним способом округлення.
Необхідність виконання “довгих” операцій , що визначає швидкодію формування векторів, суттєво обмежує застосування методу.
При використанні методу ЦДА відношення Р=DY/DХ знаходять в циклі підготовки , а операцію множення на Х заміняють накопичуючим підсумовуванням . Очевидно, що при DХ≥DY
значение Р≤0. Якщо в результаті накопичуючого підсумовування операнда DY/
При DХ<DY
знаходять відношення DХ/DY і виконують раніше перераховані дії , але вже зі зміною координат.
В методі цифрового диференційного аналізатору широко використовується також двійковий помножувач (інтегрратор послідовного переносу), назва якого визначається виконанням останнім функції виду:
![]()
де КК – значення керуючого коду, n – розрядність помножувача, fвх, fвих
Спрощена функціональна схема двійкового помножувача приведена на рис.1.2. Двійковий помножувач ДУ забезпечує перетворення управляючого коду КК в кількість імпульсів, які формуються на його виході за Т=2n тактів лічби.
Двійковий помножувач включає двійковий лічильник СТ2 та логічну схему, до складу якої входять елементи І та елемент АБО. За цикл перерахунку лічильника СТ2 на його виходах буде сформовані імпульсні послідовності(рис. 1.3), кількість імпульсів в яких дорівнюють степеням двійок( утворюють двійкові розряди).
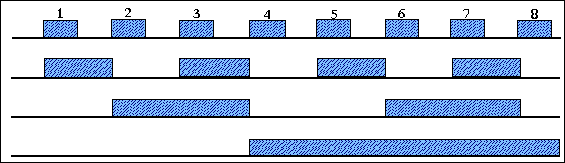
Рис. 1.3.
Часова діаграма роботи трьохрозрядного двійкового лічильника
Одиничні значення розрядів керуючого коду КК дозволяють роботу відповідних елементів І, що обумовлює проходження на їх вихід імпульсних послідовностей , які генеруються на виходах лічильника.
Елемент АБО забезпечує об’єднання імпульсних послідовностей в вихідний потік
Fвих за Т=2n тактів на виході двійкового помножувача буде сформовано КК імпульсів.
В даному підході використовується допоміжна змінна - час Т, який визначається циклом перерахунку двійкового помножувача. СТ2. Оскільки реалізується рівняння прямої, заданої в параметричній формі, то лінійні інтерполятори тікого класу часто називають параметричними.
Структурна схема параметричного лінійного інтерполятора приведена на рис.1.4.
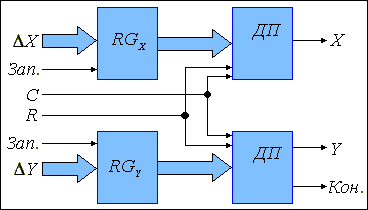
Рис. 1.4. Структурна схема параметричного лінейного інтерполятора.
Інтерполятор включає два регістри для зберігання приростів заданого вектора, які є керуючими кодами для ДП, а також два двійкових помножувача. Останні за 2n тактів формують на своїх виходах кількість імпульсів, які рівні заданим приростам.
На рис.1.5 приведений приклад формування параметричним лінійним інтерполятором відрізка прямої з DХ=5, DY=3.
Приведений параметричний лінійний інтерполятор формує відрізки прямої, незалежно від їх довжини, за 2n
тактів, що не є доцільним. Час інтерполювання можна зменшити за рахунок нормалізації - одночасного збільшення вихідних приростів в задане число разів. При цьому цикл інтерполювання зменшують в стільки ж разів.
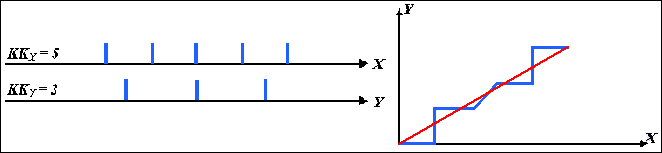
Рис. 1.5. Приклад формування відрізка прямої параметричним лінійним інтерполятором.
Розглянутий підхід орієнтований на апаратну реалізацію, має досить високу швидкодію, але сформовані траєкторії мають погану згладженість за рахунок можливого формування горизонтальних, вертикальних та діагональних кроків. Похибка інтерполювання визначається нерівномірністю надходження імпульсів на виході ДП, дискретним характером формування траєкторії і пропорційна розрядності інтерполятора.
Згідно алгоритму симетричного інтегратора обчислення інтегралу виконується приблизно, шляхом додавання ( наприклад по методу Ейлера) . При цьому обчислюються:
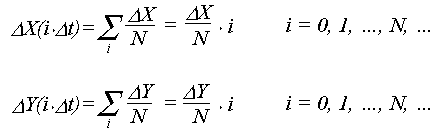
Значення N повинно бути вибрано таким, щоб кроки по DХ(iDt) і DY(iDt) були менше розміру піксела , оскільки лише в цьому випадку вектор буде виглядати як суцільна лінія. Дана умова задовольняється, якщо розмір кроку менше однієї одиниці растра. Звідси можна одержати умову для визначення N: DХ/N<1і DY/N<1,
Похибка приведеного методу полягає в тому, що прирости DX, DY необхідно ділити на N. ДДілення можна замінити зсувом, якщо прийняти величину N рівній однієї зі степенів двійки. У цьому випадку одержуємо умову:
N = log2 max(|DX|,|DY|)
На практиці в переважній більшості випадків для лінійної інтерполяції використовують метод оцінної функції. Зазначене обумовлено високою точністю інтерполяції, простотою програмної ф апаратної реаоізації і відносно високою швидкістю, обумовленою часом виконання мікрооперації підсумавування.
Загальним прийомом для всіх інтерполяторів, що працюють за методом оцінювальної функції, є аналіз знаків оцінювальної функції, на основі якого роблять крок за тією чи іншою координатою з подальшим розрахунком її нового значення і корекцією відповідної координати поточної точки.
Нехай необхідно проінтерполювати відрізок прямої, яка задана приростами Dx і Dy по осях координат
(див.рис.1.6).
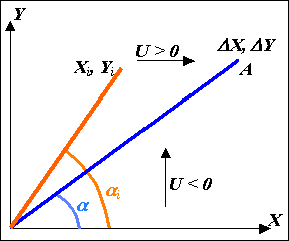
Рис. 1.6. Формировання оцінювальної функції.
Якщо точка траєкторії знаходиться вище від прямої ОА, то оцінювальна функція U>0 і наступний крок необхідно виконувати по осі X; якщо точка знаходиться нижче від цієї прямої, то U<0 і наступний крок необхідно виконувати по осі Y. Таким вимогам відповідає функція виду:
Ui = tgai – tga
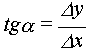
де
Тоді
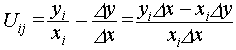
Оскільки добуток xiDx – додатній і не впливає на знак Uij,
знаменником дробу можна знехтувати. Таким чином,
Uij = yiDx – xiDy (1)
Визначимо нове значення оцінювальної функції при виконані кроку по осі X. У цьому випадку xi+1=xi+1. Після підстановки в (1.1) значення для xi+1, одержимо
Ui+1,j = yiDx – Dy(xi+1) = yiDx – xiDy – Dy = Uij – Dy
Після кроку по осі y при U<0 одержуємо нове значення yi+1=y+1. Тоді нове значення оцінювальної функції
Ui,j+1 = Dx(yi+1) – Dyxi = yiDx + Dx – xiDy = Uij + Dx
Наведений алгоритм має чотиривекторну орієнтацію крокових приростів і забезпечує похибку, не більшу від кроку інтерполювання.
Похибку інтерполювання можна зменшити, якщо використовувати діагональні крокові прирости. Такий тип приросту трактують як одночасне горизонтальне та вертикальне переміщення. Враховуючи вказане після такого кроку нове значення оцінювальної функції визначається як Ui+1,,j+1=Ui +Dx–Dу.
Ненульове початкове значення оцінювальної функції дозволяє відсиметрувати похибки інтерполювання, що зменшує її вдвічі. На рис. 1.7, а приведена невідсиметрова крокова траєкторія. За рахунок розміщення діагонального крокового приросту посередині цифрового сегмента похибка інтерполювання d1– замінюється на дві: d+ та d– (див.рис.1.7б), які значно менші від вихідної.
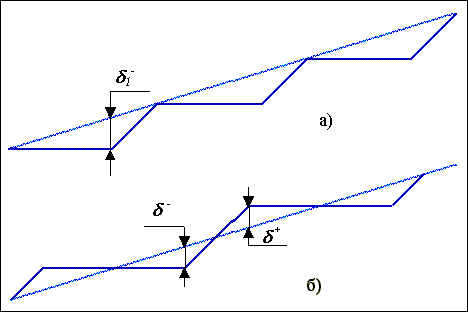
Рис.1.7. Зменшення похибки інтерполювання за рахунок симетрування.
З формули (1.1) видно, що значення оцінювальної функції визначає похибку інтерполювання. Вказане використовується в алгоритмі Томсона, згідно якого визначається оцінювальна функція для двох можливих крокових переміщень.
Дійсний крок виконується в тому напрямку, де значення оцінювальної функції менше.
Алгоритм Томпсона забезпечує максимальну точність інтерполювання, однак потребує визначення відразу двох оцінювальних функцій, що в свою чергу позначається на його обчислювальній складності.
Згідно з відомим алгоритмом Брезенхема
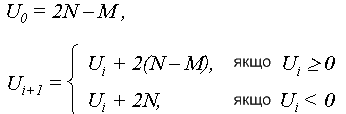
де N, M – відповідно більше і менше значення приростів відрізка.
Цикл інтерполювання закінчується після видачі M крокових приростів. Якщо Ui<0, то виконується крок по ведучій координаті, а при Ui≥0 – комбінований крок по обох координатах. Алгоритм Брезенхема забезпечує мінімальну похибку інтерполювання, що дорівнює половині кроку дискретизації, але вимагає збільшення початкових операндів вдвічі. Це в ряді випадків призводить до необхідності роботи зі словами, які перевищують розрядну сітку процесора. Цей недолік ліквідовано в алгоритмі Петуха А.М., Обідника Д.Т. (Україна).
Значення оцінювальної функції в цьому випадку розраховується згідно формул:
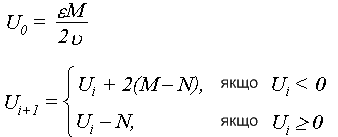
Якщо Ui≥0, то виконується крокове переміщення по ведучій координаті. В іншому випадку виконується діагональне переміщення. Аналіз кінця інтерполювання не відрізняється від вказаної процедури алгоритму Брезенхема.
Інтерполюючі пристрої формують адреси точок траєкторії в дискретному координатному просторі . На рис.1.8 приведена функціональна схема підключення інтерполятора (програмно і функціонально реалізована).
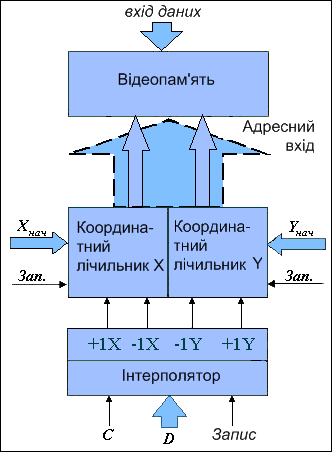
Рис. 1.8. Функціональна схема підключення інтерполятора.
Адреси точок траєкторії формують два координатних лічильника. Початкова точка Хнач, Унач заноситься в відповідні координатні лічильники в циклі підготовки і визначає їх вихідний стан. Вказана мікрооперація отримала назву позиціювання. При формуванні інтерполятором крокової траєкторії стан координатних лічильників змінюється інкрементно і визначає адресу комірки відеопам'яті. Для кожної точки траєкторії визначають код кольору , який виставляється на шину даних відеопам'яті. Для деяких режимів запис в відеопам'ять блокується.
Контрольні запитання. |
2. За який час формується відрізок прямої параметричним лінійним інтерполятором?
3. Дайте порівняльну характеристику точності методів лінійного інтерполювання.
4. Які базові операції виконуються при реалізації приведених методів лінійного інтерполювання?
5. Виконайте порівняльний аналіз відомих алгоритмів лінійного інтерполювання по методу оцінювальної функції.
6. Яким чином формують різні типи векторів -
суцільні, штрихові, штрихпунктирні?