|
1. Методи та алгоритми формування контурних зображень |
|
1.3. Методи та алгоритми формування кривих другого порядку |
|
1.3.1. Коло |
Дуги кіл , як і відрізки прямих , відносять до найбільш поширених графічних примітивів.
Існує декілька методів завдання вихідних даних для кругового інтерполювання.
Однією з можливих форм опису кола є завдання її в полярній системі координат
X = XC + R·cosQ
Y = YC + R·sinQ
де Xc,Yc – координати центра кола, R – радіус кола, Q – полярний кут.
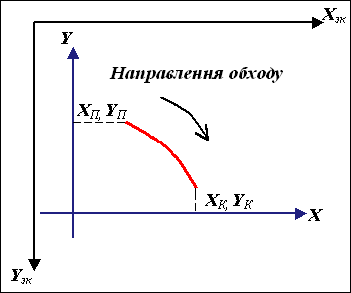
Найчастіше вказують напрямок руху (за чи проти годинниковою стрілкою), прирости координат початкової та кінцевої точки дуги кола відносно його центру, а також координати початкової точки дуги в екранній системі координат (рис. 1.9. ).

Рис. 1.9. Задання дуги кола.
При реалізації колового інтерполювання необхідно враховувати:
* коло є симетричною фігурою, що дозволяє суттєво скоротити час обчислення, оскільки для отримання всіх точок кола досить сформувати їх лише для одного октанта;
* необхідно проводити аналіз переходу через границі октантів, оскільки при цьому змінюється направлення крокових приростів (див. рис.1.10. ).
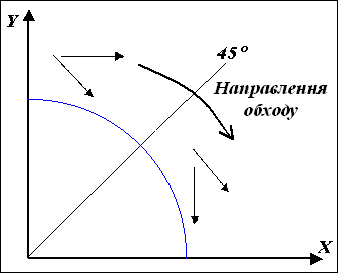
Рис.
1.10. Типи крокових збільшень
За рахунок похибки інтерполювання, а також округлень при визначені початкової та кінцевої точок дуги існує ймовірність не попадання в кінцеву точку дуги, що обумовлює необхідність ведення в обчислювальний процес режиму доведення в кінцеву точку дуги. Розглянемо процедуру формування кола в полярній системі координат. Оскільки для обчислення координат точок кола X, Y необхідно задавати дискретні значення полярного кута, то виникає проблема раціонального обрання кроку приросту цього кута – DQ. При малому кроці час побудови кола збільшується, але забезпечується висока точність відтворення кола. При великому значенні DQ якість відтворення погіршується, але час побудови зменшується. Виходячи з дискретної структури растра, можна стверджувати, що мінімальна відстань між сусідніми точками кола не може бути меншим від 1. Отже всі точки кола, без пропусків, будуть відтворені, за умови, що крок приросту полярного кута обиратиметься із умови:
![]()
Для скорочення часу формування кола із обчислювальної процедури бажано виключити громіздке обчислення тригонометричних функцій cosQ
і sinQ. Для цього обчислимо чергову i+1 точку кола у вигляді:
Xi+1 = R·Cos(Q+DQ)Yi+1 = R·Sin(Q+DQ)
Після заміни отримаємо:
Xi+1 = Xc + (Xi – Xc)CosDQ – (Yi – Yc)SinDQYi+1 = Yc + (Xi – Xc)SinDQ – (Yi – Yc)CosDQ
Отримані рекурентні співвідношення для даного підходу забезпечують максимальну швидкість обчислень , так як значення sinDQ и cosDQ &розраховуються лише один раз. Згідно прямого методу , координати точок траєкторії кола визначаються з використанням виразу виду:
Х2+Y2=R2,
де Х,
Y –
поточні точки кола,
а R – його радіус.При
Х≥В
значення абсциси послідовно збільшують на одиницю, а ординату обчислюють по формулі
Y=√ R2+X2
а при Х<Y
для поточного Y обчислюють значення
Y=√ R2+H2
Похибка інтерполювання визначається кількістю розрядів, відведених
для обчислення ,а також способом округлення
.
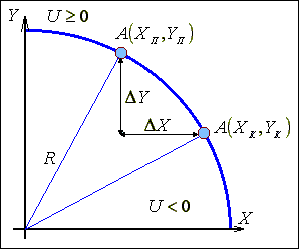
Рис.
1.11. Принцип формування оцінювальної функції.
Для реалізації функції колового інтерполювання найбільш часто використовують метод оцінювальної функції . Вид оцінювальної функції вибирають таким чином, щоб всеридині та за колом вона мала протилежні знаки, а на самому колі- нульове. Таким вимогам відповідає функція виду:
Uij = X2 + Y2 – R2
При
U
Ui+1,j = (Xi + 1)2 + Yi2 – R2 = Xi2 + Y i2 – R2 + 2Xi + 1 = Uij + 2Xi + 1
Після кроку по осі Y нове значення оцінювальної функції можна визначити, підставивши у формулу для Uij
замість
Yi
величину
Yi+1=Yi–1.
Ui+1,j = Xi + (Yi – 1) – R2 = Uij – 2Yi + 1
Таким чином, після кроку по oci X о значення оцінювальної функції необхідно додати величину2Xi+1, a після кроку по oci Y величину
–2Yi+1.
Таким чином, у будь-якому випадку додається одиниця і прямий чи доповняльний код величин
2Xi,
2Yi. Після цього необхідно скорегувати значення
Xi, Yi
для одержання Xi+1=Xi+1,
Yi+1=Yi–1. При реалізації алгоритму з восьмивекторною орієнтацією крокових приростів діагональний крок формують шляхом одночасного елементарного переміщення по обом координатам. В цьому випадку нове значення оцінювальної функції обчислюють по формулі:
Ui+1,j = Uij + 2Xi + 1 – 2Yi + 1= Uij + 2(Xi – Yi) + 2
На практиці широкого
поширення набув алгоритм колового інтерполювання співробітника фірми ІВМ Брезенхема.
При формуванні кола в другому октанті в напрямку годинникової стрілки виконуються наступні дії: U:=3–2R, X:=0,
Y:=R. Якщо
U<0, то U:=U+4X+6,
X:=X+1.В протилежному випадку U:=U+4(Xi–Yi)+10,
X:=X+1,
Y:=Y–1. Вказані дії виконують до формування кінцевої точки октанта.
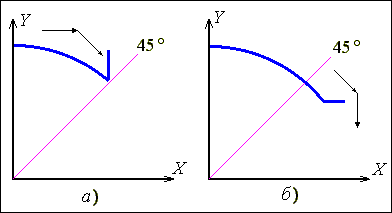
Рис.
1.12. Доведення в кінцеву точку дуги
В другому октанті (рис.1.12, а) крокова траєкторія формується горизонтальними та діагональними (комбінованими) кроковими приростами. Враховуючи, що діагональний приріст включає переміщення по осі Х,
то можна констатувати, що всі елементарні кроки до точки Х=Y
включають переміщення по осі абсцис. Звідки випливає, що при формуванні траєкторії гарантовано буде досягнуто координату Хк,
а доведення буде необхідне до координати Yк.
Аналогічно можна показати, що при формуванні дуги в першому октанті доведенню підлягає координата Хк.
|
Контрольні запитання. |
1. Приведіть характерні особливості колового інтерполювання.
2. Які форми завдання дуг кіл вам відомі ?
4. Чим обумовлена необхідність доведення в кінцеву точку дуги?
5. Поясніть, чому формули для розрахунку точок траєкторії кола різні при різних напрямках обходу.