2. Процедури машинної графіки
2.2. Алгоритми відсікання векторів
Область системи координат, в якій формується зображення для виводу на графічні засоби, називається вікном, а область прикладної системи координат, на яку відображається вікно, - областю індикації.
Відсікання – операція, яка відкидає частину зображення, що лежить поза вікном. Його можна виконувати як до перетворення зображення, так і після нього. Відсікання, яке виконують до відображення, забезпечує економію часу за рахунок того, що невидимі лінії не підлягають перетворенням. Якщо сторони вікна похилі відносно координатних осей, то алгоритм відсікання потребує відносно складних обчислень, тому відсікання невидимих частин повернутого зображення виконують після відображення.
Якщо зображення задається як список точок, то кожна точка зображується чи відкидається в залежності від результату порівняння її координат з координатами області індикації. Якщо зображення задається як множина відрізків прямих, задача буде складною. Вікно називається регулярним , якщо воно має форму прямокутника зі сторонами, які паралельні осям координат екрана.
Враховуючи, що для формування графічних зображень найчастіше використовуються відрізки прямих, розглянемо відсікання вказаного типа примітивів.
Внаслідок того, що область індикації, як правило, має форму прямокутника, відрізку належить не більш як одна видима частина.
Для реалізації відсікання необхідно знайти координати точки перетину сторін вікна з відрізком і відкинути ту його частину, яка знаходиться за вікном.
В машинній графіці найбільш часто використовуються прямокутні вікна, які задаються рівняннями їх сторін (рис.2.3).
X = XЛ, Х = ХП,
Y = YЛ, Y = YП.
Підставляючи в рівняння відрізка прямої Y=k·Х+b значення XЛ, ХП знаходять ординати перетину відповідно з лівою та правою границями вікна. Аналогічно знаходять і точки перетину з верхньою та нижньою границями вікна. Для цього в рівняння прямої підставляють відомі значення YЛ, YП.
Відрізки прямих можуть повністю знаходитись всеридині або зовні вікна. Для таких випадків розв’язувати систему рівнянь недоцільно. Взагалі рекомендується обчислювати перетин відрізка прямої з вікном в останню чергу, оскільки для цього необхідно великий об’єм розрахунків.
Провести тестування повної видимості чи невидимості відрізків можна за допомогою алгоритму Д. Коена і А. Сазерленда.
Він грунтується на тому, що кожен відрізок чи повністю лежить в межах області індикації, чи його можна розділити так, щоб одна з його частин була повністю відкинута.
ля перевірки на відсікання границі області індикації проводять так, щоб вони ділили поле, на якому знаходиться зображення, на дев’ять підобластей. Кожній з них присвоюють чотирирозрядний код. Цей код присвоюють кінцевим точкам відрізка, який знаходиться у відповідних підобластях:
1
0 0 1 1
0 0 0 1
0 1 0
0 1 0 1 0 1 0 0 0 1 1 0
Одиниці у відповідних розрядах коду означають:
* першому – точка над верхнім краєм області індикації;
* у другому – точка під нижнім краєм області індикації;
* у третьому – точка праворуч від області індикації;
* ; у четвертому – точка зліва від лівого краю області індикації.
Розглянемо характерні випадки.
1. Чотирьохрозрядні коди граничних точок відрізка прямої AB,
який повністю належить вікну (рис.2.3),
нульові.
Таким чином, якщо чотирирозрядні коди для обох кінців відрізка дорівнюють нулю, то відрізок повністю лежить в області індикації.
2.
Чотирьохрозрядні коди граничних точок відрізка прямої, який розміщений по одну із сторін вікна ( рис. 2.3. Відрізок QL),
співпадають . Для встановлення вказаного достатньо виконати операцію логічного множення цих двох кодів, яка для вказаного випадку дасть ненульовий результат.
3.
Чотирьохрозрядні коди граничних точок відрізка прямої, який частково знаходиться в області індикації ( рис. 2.3 , відрізки KD,
HZ)
не співпадають. Тому, результат логічного множення цих кодів дасть нульовий результат.
Для вказаного випадку необхідно виконати відсікання. Координати точки відрізка, яка належить одній із границь вікна, знаходять із рівняння відрізка y=k·x+b
підстановкою в нього відповідних координат граничних точок вікна і знаходженням невідомої координати.
Для відрізка HZ знаходять точку перетину
F, яка ділить відрізок на два співставних. Надалі для кожного отриманого відрізка виконуємо алгоритм Коена-Сазерленда. В результаті аналізу відрізок FZ
відкидається.
Найбільш складним для відсікання є випадок, коли відрізок прямої двічі перетинає границі вікна (рис. 2.3 , відрізок KD). В цьому випадку алгоритм Коена-Сазерленда виконується для трьох співставних відрізків – KE, EP, PD.
4. Якщо відрізок прямої лежить за областю вікна і при цьому його граничні точки не належать однаковим підобластям (рис. 2.3 , відрізок SV), то результат логічного множення чотирьохрозрядних кодів дасть нульовий результат. Для визначення повної видимості необхідно перевіряти значення кодів обох кінців окремо.
Один із шляхів визначення точки перетину відрізка прямої з границями вікна зводиться до вирішення системи рівнянь, яка включає рівняння заданого відрізка прямої та відрізків, які є граничними для вікна. При цьому виконуються операції множення чи ділення, реалізація яких вимагають обчислювальних засобів, та великих затрат часу. Вказаного можливо уникнути, якщо реалізувати двійковий пошук такого перетину шляхом ділення заданого відрізка пополам. Ділення на 2 еквівалентно зсуву операнда на один розряд в сторону розрядів з меншою вагою.
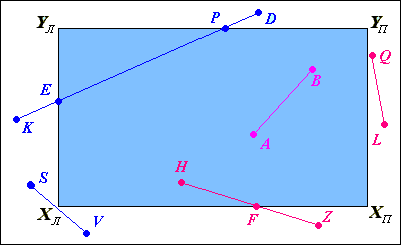
Рис. 2.3. Розміщення відрізків прямих відносно вікна
Алгоритм був запропонований Спрулом і Сазерлендом і включає в себе співсоставним алгоритм Коена-Сазерленда. Алгоритм використовується тоді, коли алгоритм Коена-Сазерленда не дав позитивних результатів на предмет приналежності відрізка вікну або його розташування за вікном
вне окна.
В алгоритмі відсікання методом ділення відрізка пополам використовуються коди кінцевих точок відрізка і перевірки, які виявляють повну видимість відрізків, наприклад відрізок a на рис.2.4, і тривіальну невидимість відрізків, наприклад відрізок b на рис.2.4.
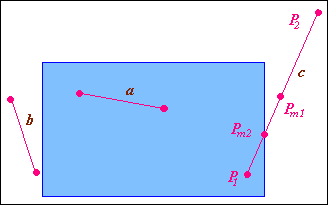
Рис.
2.4.
Реалізація відсікання згідно алгоритму ділення відрізка пополам
Ті відрізки, які за допомогою таких простих перевірок не можна віднести до одної з двох категорій, розбиваються на дві рівні частини. Координати середньої точки розбиття обраховуються за формулами:
Xm = (X2+X1)/2,
Ym = (Y2+Y1)/2.
Аналогічні дії застосовуються до кожних одержаних половин відрізків до тих пір, поки не буде виявлено перетин з однією із сторін вікна або довжина відрізка, що розглядається, стане занадто малою, тобто, поки вона не перетвориться в точку. Кількість кроків даного алгоритму дорівнює log2N,
де
N –
довжина відрізку.
Даний метод проілюстрований на прикладі відрізка с
(рис.2.4). Точка Р1
запам’ятовується, як поточна видима точка, а відрізок с
розбивається пополам точкою Pm1.
Відрізок Р2Pm1
відкидається, як невидимий, а відрізок Р1Pm1
розбивається пополам точкою Pm2.
Відрізок Pm1Pm2
відкидається, а в вікні залишається відрізок P1Pm2
тому, що перевірка по алгоритму Коена-Сазерленда виявляє, що даний відрізок повністю лежить в області індикації.
Контрольні
запитання.
1.
В чому полягає процедура відсікання?
2.
Чим обумовлена поява метода ділення відрізка пополам?
3.
Які дії виконується згідно метода Коена-Сазерленда?