2. Процедури машинної графіки

2.1. Афінні перетворення

Афінні перетворення знаходять широке застосування в задачах машинної графіки. Найбільшого поширення набули часткові випадки афінних перетворень: зсув, поворот, масштабування.

Нехай у площині задана початкова система координат 0ХY і деяка нова система координат 0₁X₁Y₁. Тоді перетворення, які полягають у тому, щоб у відповідність точці P площини ставиться точка P₁, яка в новій системі має такі самі координати, що й точкаP у початковій, називаються афінними.

Основні властивості афінних перетворень:

*  Множина точок, яка в початковій системі координат задовольняє деяке рівняння, переходить у множину точок, координати яких у новій системі задовольняють таке саме рівняння. Так, пряма переходить у пряму, площина у площину;

*  Відношення площ і об’ємів геометричних фігур зберігається;

*  Зберігається просте співвідношення трьох точок;

*  Існує єдине перетворення площини, що переводить трійку точок, які не належать одній прямій, у нову трійку точок, які також не належать прямій;

*  Якщо початкова та нова системи координат є декартовими з однаковими одиничними відрізками по осях, то при перетвореннях зберігаються всі метричні властивості геометричних фігур.

На рис.2.1 зображені геометричні співвідношення між початковою системою 0XY і системою 0X₁Y₁, яку одержали при повороті початкової системи на кут a.

За допомогою співвідношень на рис. 2.1 одержуємо систему рівнянь 

яку можна зобразити в матричному вигляді:

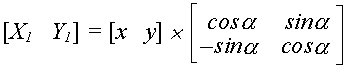
При повороті зображення не завжди одержують цілочислові координати, що приводить до необхідності їх округлення.

Функціональний метод повороту зображення виключає з обчислювального процесу виконання синусно-косинусних перетворень та «довгих» операцій.

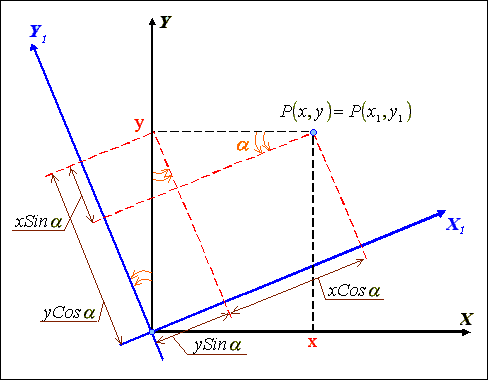
Рис. 2.1. Поворот системи координат

Сутність методу полягає в наступному.

Декартова площина 1  і відповідна їй система координат ХОY утворена площиною екрану індикатору зображення, а декартова площина 2  і відповідна їй система координат Х¹О¹Y¹ – площиною матриці світлочутливих елементів (рис.2.2).

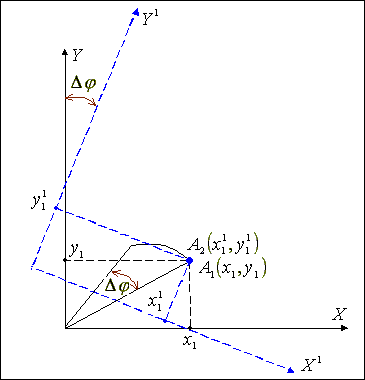
Рис. 2.2. Функціональний метод повороту

В початковий момент часу точка А1 з координатами Х1, Y1 відображається на екрані індикатору. Матриця світлочутливих елементів, яку повернуто по відношенню до екрану на кут Dj, сприймає точку в системі координат Х¹О¹Y¹, по відношенню до якої остання має координати Х¹1, Y¹1. Очевидно, що відображаючи на екрані точку з координатами Х¹1, Y¹1, здійснюється поворот вихідної точки на кут Dj  в системі координат ХОY. Виконуючи вказану процедуру для всіх точок зображення, за час одного кадру здійснюється поворот зображення на кут Dj.

За рахунок повторення процесу n разів, де n=j/Dj, забезпечується поворот зображення на заданий кут j.

Оскільки вихідна та нова системи координат є прямокутними декартовими з однаковими одиничними відрізками по осям, то при перетворенні зберігаються всі метричні властивості геометричних фігур.

Недолік функціонального методу повороту полягає у відносно великій похибці перетворення.

При масштабуванні здійснюють збільшення або зменшення розмірів зображення згідно з перетвореннями виду

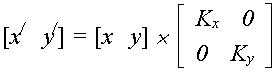
де K_x , K_y – масштабні коефіцієнти.

При K_x=K_y=K здійснюється перетворення подібності. Зображення збільшується в K разів при K>1 і зменшується при K<1.

Точка зсувається додаванням до кожної координати точки додатної або від'ємної константи:

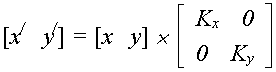
де m, n – значення параметрів зсуву.

Контрольні   запитання.

1.  Які перетворення відносять до афінних?

2.  Які основні властивості афінних перетворень?

3.  Приведіть формули для повороту точки зображення на кут a проти годинникової стрілки.

4.  Чи можливе суміщення в одній процедурі різних типів афінних перетворень?

5.  Як організується скролинг вікна зображення ?

     Зміст