3. Методи побудови поверхонь
3.1. Представлення поверхні полігональною сіткою
Полігональна сітка являє собою сукупність ребер, вершин і багатокутників. Вершини з'єднуються ребрами, а багатокутники розглядаються як послідовності ребер або вершин. Сітку можна задавати декількома різними способами .Прикладному програмісту варто обрати спосіб, який найбільш підходить для його задачі. Зрозуміло, в одній задачі може з однаковим успіхом використовуватись одразу декілька представлень : для зовнішньої пам'яті, внутрішнього використання і користувача. Для оцінки цих представлень використовуються наступні критерії:
* Об'єм потрібної пам'яті;
* Легкість ідентифікації ребер ;
* Легкість ідентифікації багатокутників, яким належить дане ребро;
* Легкість процедури пошуку вершин, що утворюють ребро;
* Легкість визначення всіх ребер, що утворюють багатокутник;
* Легкість отримання зображення полігональної сітки;
* Легкість знаходження помилок в представленні (наприклад, відсутність ребра, вершини чи багатокутника).
В загальному випадку, чим більш явно виражені залежності між багатокутниками, вершинами і ребрами, тим швидше виконують операції над ними і тим більше пам'яті потребує відповідне представлення. В деяких випадках ребра полігональних сіток є спільними для більш чим двох багатокутників (рис. 3.1.).
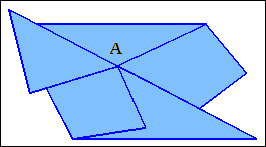
Рис.
3.1. Множина багатокутників зі спільним ребром.
Розглянемо три найбільш поширені способу опису полігональних сіток.
1. Явне завдання багатокутників.
Кожен багатокутник можна подати у вигляді списку координат його вершин:
P =
((X1,Y1,Z1), (X2,Y2,Z2), ..., (XN,YN,ZN)).
Вершини запам'ятовуються в тому порядку, в якому вони зустрічаються при обході навколо багатокутника. При цьому всі послідовні вершини багатокутника, а також перша і остання з'єднуються ребрами. Для кожного окремого багатокутника даний спосіб запису є ефективним, але для полігональної сітки дає великі втрати пам'яті внаслідок дублювання інформації про координати спільних вершин. Більш того, явного опису спільних ребер і вершин просто не існує. Наприклад, пошук всіх багатокутників які мають спільну вершину, потребує порівняння трійок координат одного багатокутника з трійками координат решти багатокутників. Найбільш ефективний спосіб виконати таке порівняння полягає в сортуванні всіх N
координатних трійок : для цього потрібно в кращому випадку N•Log2•N
порівнянь. Але й тоді існує небезпека того, що одна і та ж вершина внаслідок помилок округлення може в різних багатокутниках мати різні значення координат, тому вірна відповідність може бути не знайдена. Полігональна сітка зображується шляхом креслення ребер кожного багатокутника, але це призводить до того, що спільні ребра малюються двічі - по одному разу для кожного з багатокутників. Окремий багатокутник зображується тривіально.
2.
Завдання багатокутників за допомогою покажчиків.
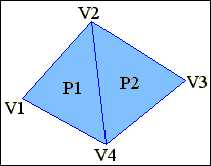
При використанні цього представлення кожен вузол полігональної сітки запам'ятовується лише один раз в списку вершин V=((X1,Y1,Z1),...,(XN,YN,ZN)). Багатокутник визначається списком покажчиків (або індексів) в списку вершин. Багатокутник складений з вершин3, 5, 7 і 10 цього списку представлений як P=(3,5,7,10). На рис. 3.2 наведений приклад такого представлення. Воно має ряд переваг в порівнянні з явним завданням багатокутників. Оскільки кожна вершина багатокутника запам'ятовується тільки один раз, вдається зберегти значний об'єм пам'яті. Крім того, координати вершини можна легко змінювати. Але все ще не просто знаходити багатокутники з спільними ребрами; останні при зображенні всієї полігональної фігури малюються двічі. Ці проблеми можна вирішити, якщо робити опис ребер в явному вигляді.
|
Рис. 3.2. Завдання багатокутників за допомогою покажчиків с помощью указателей |
V=(V1,V2,V3,V4)=((X1,Y1,Z1),...,(X4,Y4,Z4)), P1=(1,2,4), P2=(4,2,3).
|
3. Явне завдання ребер.
В цьому представленні є список вершин V,
однак, будемо розглядати тепер багатокутник не як список покажчиків на список вершин, а як сукупність покажчиків на елементи списку ребер, в якому ребра зустрічаються лише один раз. Кожне ребро в списку ребер вказує на дві вершини в списку вершин, що визначають це ребро, а також на один чи два багатокутника, яким це ребро належить. Таким чином ми описуємо багатокутник як P=(E1,..,EN), а ребро як E=(V1,V2,P1,P2).
Якщо ребро належить лише одному багатокутнику, то або P1
або P2
–
пусте. На рис.3.3 приведений приклад такого представлення.
такого
представления.
При явному завданні ребер полігональна сітка зображується шляхом креслення не всіх багатокутників, а всіх ребер. В результаті вдається запобігти багатократному кресленню спільних ребер. Окремі багатокутники при цьому також зображуються досить просто.
|
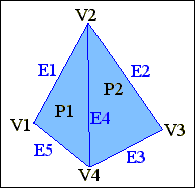
Рис. 3.3. Явне завдання ребер полігональної сітки |
V=(V1,V2,V3,V4)=((X1,Y1,Z1),...,(X4,Y4,Z4)), E1=(V1,V2,P1,L),
E2=(V2,V3,P2,L), E3=(V3,V4,P2,L), E4=(V4,V2,P1,P2), E5=(V4,V1,P1,L), P1=(E1,E4,E5),
P2=(E2,E3,E4). |
В жодному з цих представлень задача визначення ребер, інцидентних вершині, не є простою - для її розв'язання необхідно перебрати все ребра. Звичайно, для визначення таких відношень можна безпосередньо використовувати додаткову інформацію.
Наприклад, в представленні, запропонованому Бомгартом, використовується розширений опис ребер, що включає покажчики на два сусідніх ребра кожного багатокутника, а також опис вершин, що включає покажчик на (довільне) ребро, інцидентне вершині. В результаті ми маємо більше інформації про багатокутниках і вершинах.
При роботі з багатокутниками використовують рівняння площини, де лежить багатокутник.
Рівняння площини в просторі має вид Ax+By+Cz+D=0.
Для завдання площини достатньо трьох точок.
Якщо задано 3 точки, то маємо систему рівнянь:
Ax1
+
By1
+
Cz1
+
D
=
0,
Ax2
+
By2
+
Cz2
+
D
=
0,
Ax3
+
By3
+
Cz3
+
D
=
0.
Якщо три точки не колінеарні, то рівняння має розв’язок відносно
А,
В, С і
D,
якщо присвоїти яке-небудь значення одному з коефіцієнтів. Наприклад, припустимо, що D=1 і розв’яжемо систему рівнянь.
Більш раціональне рішення грунтується на тому, що, якщо точки Р1, Р2, Р3 і (x,y,z) знаходяться в одній площині, то
Ax
+
By
+
Cz
+
D
=
0,
Ax1
+
By1
+
Cz1
+
D
=
0,
Ax2
+
By2
+
Cz2
+
D
=
0,
Ax3
+
By3
+
Cz3
+
D
=
0 .
Для вказаної системи рівнянь запишемо:
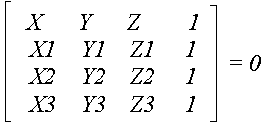
Детермінант можна представити у вигляді:
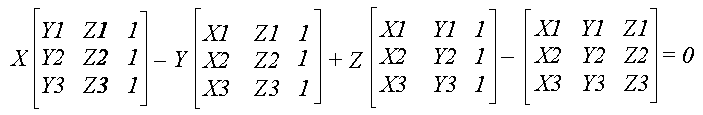
Звідки випливає, що невідомі коефіцієнти А, В, С і D дорівнюють відповідним детермінантам. Обчислення останніх дозволяє достатньо легко задати площину в координатному просторі.
Контрольні
запитання.
1. Дайте порівняльну характеристику різних форм завдання полігональної сітки.
2. Який основний недолік представлення поверхні полігональною сіткою ?
3. Чим визначається точність представлення поверхні полігональною сіткою ?
4. Яким чином задається площина ?