3. Методи побудови поверхонь

3.2. Фактурні побудови

В машинній графіці фактурою називають деталізацію побудови поверхні. Найбільшого розповсюдження отримали наступні два способи деталізації.

Перший полягає в тому, що на рівну поверхню наносять раніше заданий візерунок. Після цього поверхня все одно залишається рівною. Накладання візерунка на рівну поверхню виконується за допомогою функції відображення.

Другий спосіб деталізації заключається у створенні нерівностей на поверхні. Такі шорсткі поверхні реалізуються шляхом внесення зміни у параметри, котрі задають поверхню.

Вперше метод для нанесення візерунка на поверхню запропонував Кетмул.

Головним при нанесенні на поверхню є відображення, тому в даному випадку задача приводиться до перетворенню системи координат.

Якщо малюнок заданий в прямокутній системі координат (u,w), а поверхня в другій прямокутній системі координат (Q,j), то для нанесення малюнка на поверхню треба знайти чи задати функцію відображення одного простору на другий.

Q=f(u,w),       j=g(u,w)

або

j=r(Q,j),     W=S(Q,j).

Звичайно, хоча й необов’язково, передбачається, що функція відображення лінійна: Q=Au+B, j=Cw+D, де коефіцієнти A, B, C, D знаходять з співвідношення між двома відомими точками в системах координат.

Розглянемо конкретний приклад.

Візерунок являє собою просту сітку з прямих, які перетинаються (рис.3.4) . Параметричне представлення октанти сфери:

X = sin sinj,

Y = cosj,

Z = cos sinj.

Нехай функція відображення лінійна, тобто

Q = Au + B,         j = Cw + D

і кути візерунка переходять в кути октанта  

u = 0,    w = 0    при    Q = 0,        j = p/2,

u = 1,    w = 0    при    Q = p/2,     j = p/2,

u = 0,    w = 1    при    Q = 0,        j = p/4,

u = 1,    w = 1    при    Q = p/2,     j = p/4.

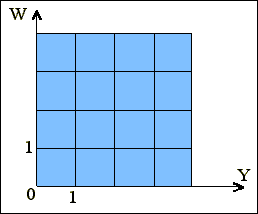
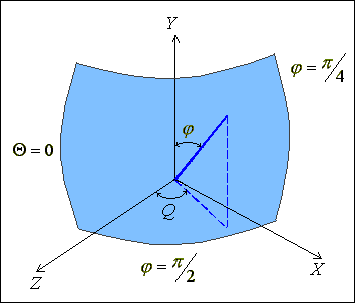
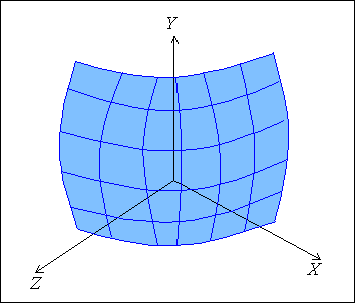
Рис. 3.4. Формування поверхні

Звідки A=p/2, B=0, C= -p/4, D=p/2.

Зворотне перетворення має вид u=Q/(p/2), w=(p/2–j)/p4.

У цьому методі малюнок наноситься на рівну поверхню, і вона після цього залишається рівною. Для того щоб поверхня здавалася нерівною, можна відцифрувати фотографію нерегулярною фактурою і відобразити її на поверхню.

Блінк будує нову поверхню, котра має вигляд нерівної, записуючи у направлення нормалі функцію обурення P(u,w).

В якості Р можна використовувати майже кожну функцію, в якій присутні часткові похідні.

Одним з останніх методів будування нерегулярностей базуються на фрактальних поверхнях. Фрактальна поверхня будується з випадково заданих полігональних чи біполімінальних поверхонь. За допомогою фрактальних поверхонь малювалися природні об’єкти – каміння, дерева, хмари. 

Контрольні   запитання.

1.  Яку функцію найбільш доцільно вибрати для функції відображення ?

2.  Як задається фактурна сітка ?

3.  Які методи застосовують для побудови широховатих поверхонь ?

     Зміст