3. Методи побудови поверхонь

3.3. Формування параметричних бікубічних поверхонь

Бикубичні поверхні задаються кубічними рівняннями від двох змінних s і t. Змінюючи обидва параметри від 0 до 1, визначають всі точки на частині поверхні.

Будем використовувати рівняння для х: 

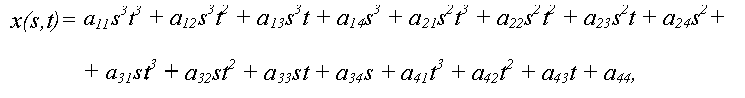
Запишем його в більш зручній формі: x(s,t)=SC_xT^T, де S=[s³ s² s 1], T=[t³ t² t 1], а T^T позначує транспоновану матрицю T. Приведений запис називають алгебраїчною формою представлення, оскільки C_x задає коефіцієнти бікубічного багаточлена. Існують також C_y та C_z, які визначають коеффіцієнти y(s,t) и z(s,t).

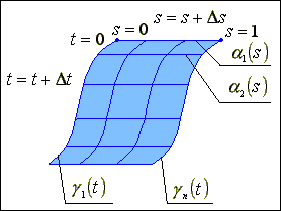
Для a_i(s)   s = 0..1

Для g_j(t)    t = 0..1

g₁(t) і g_n(t) є граничними точками для кривих a_i(s), Dt і Ds вибираються довільно. Чим менші значення зазначених параметрів, тим більш точно буде визначена форма поверхні и тим більший об’єм обчислень буде необхідно. 

Контрольні   запитання.

1.  Приведіть рівняння бікубічної поверхні.

2.  Чим визначається точність завдання бікубічної поверхні?

3.  Як формується бікубічний кусок поверхні ?

     Зміст