4. Методи побудови реалістичних трьохвимірних зображень
4.2. Алгоритми тріангуляції
Майбутнє машинної графіки пов'язано з формуванням реалістичних тривимірних зображень. Необхідність їх формування виникає в багатьох областях діяльності людини, наприклад, в машинобудівному та архітектурному моделюванні, дизайні, рекламі, мультиплікації і т.д. Інтерес до синтезу тривимірних (3D) зображень пояснюється тим, що вони найбільш реально відображають навколишню дійсність. 3D зображення найбільш інформативні, оскільки дозволяють оцінити конструктивні і естетичні особливості об'єктів. Системи синтезу реалістичних зображень повинні забезпечувати передачу всіх властивостей модельованих об'єкта: об'ємність, розташування, передачу півтонів, тіні, освітлення, текстури поверхні. Чим вище ступінь реалістичності зображення, тим більше потрібно обчислень для його формування.
Генерація об'ємних зображень представляє складну обчислювальну задачу, у зв'язку з чим на практиці виконують її декомпозицію. Складні зображення формують фрагментарно, для чого їх розбивають на складові частини. Процес розбиття поверхні об'єктів на полігони отримав назву тесселяціі. Ця стадія на даному етапі розвитку машинної графіки проводиться повністю програмно незалежно від технічного рівня 3D-апаратури.
В даний час з'явилася велика різноманітність графічних акселераторів, які мають апаратні засоби для зафарбовування тривимірних об'єктів, видалення невидимих частин, накладення текстур та інші графічні функції. Для використання переваг 3D-прискорювачів необхідно програмно призвести тесселяцію початкових об'єктів, передаючи отримані полігональні області для подальшої обробки акселератором.
На практиці найбільш часто здійснюється розбиття зображень на трикутники. Це пояснюється наступними причинами:
* Трикутник є найпростішим полігоном, вершини якого однозначно задають межу;
* Будь-яку область можна гарантовано розбити на трикутники;
* Обчислювальна складність алгоритмів розбиття на трикутники істотно менше, ніж при використанні інших полігонів;
* Реалізація процедур рендерингу найбільш проста для області, обмеженої трикутником;
* Для трикутника легко визначити три його найближчих сусіда, що мають з ним спільні грані.
Процес розбиття полігональної області зі складною конфігурацією в набір трикутників називається тріангуляції. При аналізі або синтезі складних поверхонь їх апроксимуються сіткою трикутників, згодом чого у подальшому оперують з найпростішими полігональних областями.
Особливий інтерес до алгоритмів тріангуляції визначається тим, що вони використовуються в багатьох процедурах машинної графіки, таких як зафарбування, видалення невидимих частин, відсікання, формування поверхонь.
Наведемо приклад створення півсфери, проілюструвавши етапи рендеринга. Полігональна область (рис.4.1а) представляється сукупністю трикутників (рис.4.1б). При цьому важливо досить точно апроксимувати зовнішній контур.
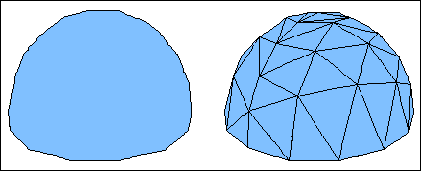
Рис. 4.1 а) полігональна область б) тріангуляційних мережа
Будь-яка поверхня може бути апроксимувати з необхідною точністю сіткою трикутників. Точність апроксимації визначається кількістю трикутників і способом їх вибору. Для якісної візуалізації об'єкта, що знаходиться поблизу точки спостереження, потрібно врахувати у багато разів більше трикутників, ніж у ситуації, коли той самий об'єкт розташований на відстані. Навіть досить груба сітка корисна на практиці, так як методи згладжування, що застосовуються в процесі відображення, можуть значно поліпшити уявлення про кривизні поверхні.
Наступний етап - зафарбовування граней (рис.4.2), обмежених трикутниками.

Рис.4.2. Зафарбовування граней об'єкту
Останнім етапом є застосування алгоритмів згладжування, які усувається ребристої поверхні, ефект Маха. На рисунку 4.3 представлена вже гладка півсфера з плавним переходом напівтонів і областями освітлення.

Рис.4.3. Згладжування поверхні
При моделюванні об'єкта виникає задача, яку кількість трикутників потрібно використовувати? З одного боку, потрібно досягти максимальної якості при остаточному візуалізації, а з іншого знизити навантаження на процесор і 3D-акселератор. Для зниження навантаження можна використовувати менш деталізовану тріангуляційних мережу, але при цьому якість буде далеко не найкращим.
При формуванні динамічних зображень точність представлення об'єктів у кадрі з-за його переміщення не сприймається людиною, у зв'язку з чим недоцільно використовувати детальну тріангуляцію.
При виборі підходів і алгоритмів тріангуляції слід керуватися метою, яка ставиться конкретним завданням. Наприклад, при моделюванні об'єкта, що знаходиться далеко, абсолютно немає сенсу застосовувати дуже детальну мережу для його опису і, навпаки, для близьких об'єктів це дуже важливо, наприклад, для побудови моделі голови людини потрібно близько 60 тис. трикутників.
Розглянемо найбільш поширені алгоритми тріангуляції полігонів. Найпростіше рішення задачі тріангуляції полягає в розщепленні полігону вздовж деякої хорди на два полігони і надалі рекурсивної розбитті їх до ситуації, коли підлягає тріангуляції полігон є трикутником.
Даний спосіб застосовується лише для тріангуляції опуклих полігонів. Опуклим вважається полігон, якщо відрізок прямої, що з'єднує будь-які його дві точки, повністю лежить у внутрішній області (рис 4.4а). Полігон на малюнку 4.4б не є опуклим, так як відрізок АВ виходить за межі багатокутника.
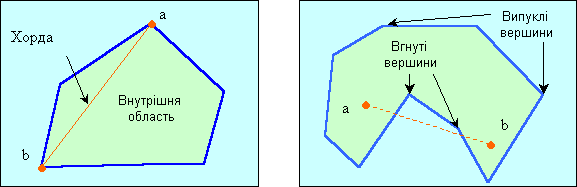
Рис.4. 4 а) Опуклий полігон б) Невипуклий полігон
Триангуляція невипуклих полігонів не так проста, тому попередня розбивка невипуклих багатокутників на опуклі істотно спрощує алгоритми їх подальшої обробки. Найпростіше це можна зробити шляхом послідовного перенесення і повороту багатокутника так, щоб одна з його вершин збігалася з початком координат, а виходить з неї сторона - з віссю Ох. При розташуванні будь-яких сторін нижче осі, відбувається їх відсіч, і алгоритм рекурсивно повторюють для отриманих полігонів, поки вони не стануть опуклими.
Наведемо універсальний алгоритм. Тріангуляції будь-якого полігону можна здійснити за наступним алгоритмом універсальному.
Вибирається крайня ліва вершина і між двома її суміжними сторонами проводиться діагональ. При цьому можуть мати місце наступні два випадки: рис.4.5а - діагональ ас є хордою; рис.4.5б - діагональ нас не хорда, так як всередину трикутника abc потрапляє вершина d полігону (у загальному випадку їх може бути декілька). З усіх вершин всередині трикутника abc вершина d найбільш віддалена від сторони ас. Цю вершину будемо називати вторгається. У разі, коли вторгається вершини немає, то отриманий трикутник заносять у сітку трикутників, і алгоритм рекурсивно обробляє залишився полігон до тих пір, поки він не виродиться в трикутник.
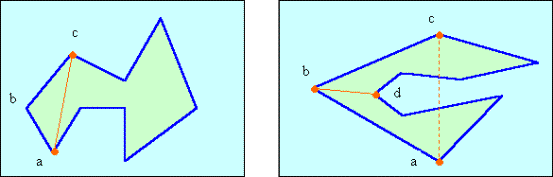
При виявленні вершини, що вторгається, проводиться діагональ з поточної до вторгається вершини. Отримані полігони рекурсивно обробляються до отримання трикутників.
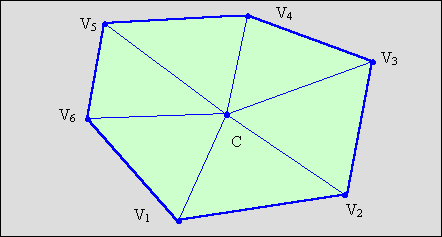
Один із підходів до тріангуляції полягає в знаходженні внутрішньої точки області, обмеженою полігоном, і з'єднанні з нею всіх вершин (рис.4.6).
Враховуючи, що тріангуляція є підготовчим етапом рендеринга, то до вибору внутрішньої точки можуть пред'являтися певні вимоги. Так, наприклад, при багатопроцесорної обробці доцільно внутрішню точку вибрати таким чином, щоб площа складових трикутників була приблизно однаковою. У цьому випадку буде забезпечена однакова ступінь обчислювальної завантаження апаратури.
В одному з найпоширенішому програмному інтерфейсі (API) для розробки додатків в області двовимірної і тривимірної графіки стандарті OpenGL для формування тріангуляційних сітки використовуються наступні команди
Рис.
4.7.
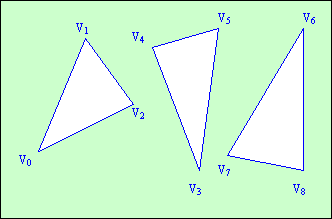
GL_TRIANGLES.
Трикутники. Команда малює серію трикутників, використовуючи трійки вершин
v0,
v1 и
v2,
потім v3,
v4 и
v5
і
т.д (рис.4.7). Якщо кількість вершин не кратно 3, точки, що залишилися, ігноруються.
GL_TRIANGLE_STRIP.
Смуга трикутників. Команда малює серію трикутників, використовуючи вершини в наступному порядку: v0,
v1, v2,
потім
v2,
v1,
v3,
потім
v2,
v3, v4,
і
т.д.
(рис.4.8). Порядок вершин повинен гарантувати, що трикутники мають правильну орієнтацію. Смуга може використовуватися для формування частини поверхні.
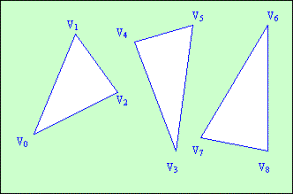
Рис.
4.8.
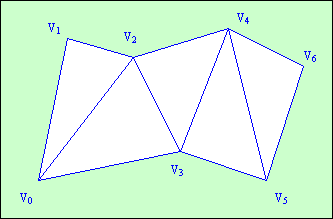
GL_TRIANGLE_FAN.
Команда схожа на GL_TRIANGLE_STRIP, але при формуванні трикутників використовують вершини в такому порядку:
v0,
v1, v2,
потім
v0,
v2, v3,
потім
v0,
v3, v4,
і
т.д.
(рис.4.9). Всі трикутники мають загальну вершину v0.
У машинній графіці завдання тріангуляції можна розглядати в двох напрямах - це тріангуляція полігональних областей і тріангуляції набору точок. Остання має місце при описі поверхні набором точок і інтенсивностями їх кольорів. Поточечное опис поверхонь застосовують у тих випадках, коли поверхня дуже складна і не володіє гладкістю, а детальне уявлення численних геометричних особливостей важливо для практики. До поверхонь такого роду можна віднести ділянки грунту, форми малих небесних тіл, мікрооб'єктів, зроблені за допомогою електронного мікроскопа та інші освіти зі складною формою.
PРозглянемо тріангуляцію точок на площині за методом Делоне. Ця тріангуляція добре збалансована в тому сенсі, що формуються трикутники прагнуть до равноугольності (ріс.4.10а). Триангульовані зображення на малюнку 4.10б не може бути віднесено до тріангуляції Делоне.
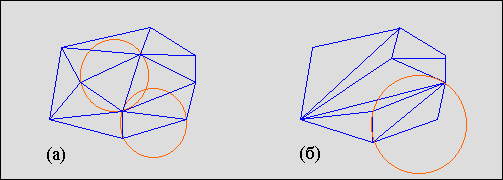
Рис.4.10. Два варіанти тріангуляції для одного набору точок
Триангуляція набору точок буде тріангуляції Делоне, якщо описана окружність для кожного трикутника буде вільна від точок, тобто всередині її не буде більше ні однієї точки з набору. На малюнку 4.10а показані дві окружності, які не містять всередині себе інших точок (можна провести кола і для інших трикутників, щоб переконатися, що вони також вільні від точок набору). На малюнку 4.10б це правило не дотримується - всередині області, обмеженої колом, потрапила одна точка іншого трикутника. Отже, ця тріангуляція не відноситься до типу Делоне.
Алгоритм працює шляхом постійного нарощування до поточної тріангуляції по одному трикутнику за крок. Спочатку тріангуляція складається з одного ребра, після закінчення роботи тріангуляція є тріангуляції Делоне. На кожній ітерації алгоритм шукає новий трикутник, який підключається до кордону поточної тріангуляції. Пошук і підключення трикутника образно можна уявити, як надування двовимірного міхура, прив'язаного до одного з ребер кордону. Якщо такий міхур досягає деякої, ще не включеної до тріангуляції точки з набору, то утворюється трикутник. У випадку, коли точка не зустрінута, обробляється наступне ребро границі.
Алгоритми тріангуляції реалізовані в багатьох професійних графічних пакетах 3D-моделювання, таких як 3D Studio MAX, OpenGL Optimizer, LightWave та ін Ці пакети дозволяють не тільки використовувати різні алгоритми для тріангуляції, але й додавати користувачам свої.
Враховуючи, що алгоритми тріангуляції є невід'ємною частиною практично всіх програмних продуктів 3D-графіки, інтенсивно ведуться роботи щодо їх удосконалення. Можна припустити, що в недалекому майбутньому вони будуть реалізовані апаратно в графічних акселераторах.
Контрольні
запитання.
1.
Які цілі переслідуються при триангуляцїі зображень?
2. Приведіть ххарактеристику основним методам триангуляції.
3. Які команди використовуються в стандарті OpenGL дяля триангуляції?