Задачний практикум

Частина 1 

В задачному практикуму наведені приклади розв'язку типових задач.  

1.   Визначити мінімальну кількість інтерполяційних тактів, необхідну для формування вектору ортогональними кроковими приростами.  

Формування вектору здійснюється вертикальними та горизонтальними кроковими приростами (рис.9.1).    

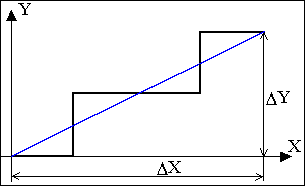       Рис. 9.1.    

Кожний із ортогональних кроків виключає переміщення по іншій координаті. Оскільки переміщення в напрямку осі абсцис здійснюється тільки горизонтальними кроками , то їх кількість дорівнює DX.  

Аналогічно, кількість інтерполяційних тактів в напрямку осі ординат дорівнює DY. Загальна кількість інтерполяційних тактів DX+DY.  

2. Виконайте інтерполювання відрізка прямої з приростами DХ=5, DY=2 по алгоритму Пєтуха А.М., Обідника Д.Т..  

Інтерполювання по алгоритму Пєтуха А.М., Обідника Д.Т. дійснюється згідно слідуючих формул:    

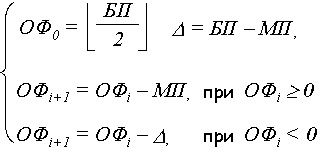
де БП і МП відповідно більше та менше значення приростів DХ, DY.  

БП = 5,      МП = 2,      D = 3.  

ОФ₀ = e5/2u = 2          ОФ₃ = –2 + 3 = 1  

ОФ₁ = 2 – 2 = 0         ОФ₄ = 1 – 2 = –1  

ОФ₂ = 0 – 2 =  -2        ОФ₅ = –1 + 3 = 2  

При ОФ_i≥0 виконується горизонтальний крок , а при ОФ_i<0 – діагональний.

Сформована траєкторія представлена на рис. 9.2.    

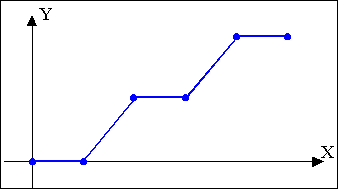    Рис. 9.2.  

3.   Визначити тип вектору, який формується вертикальними та діагональними кроками, для якого знак оцінювальної функції в кожному інтерполяційному такті змінюється на протилежний, а значення адрес пікселів зменшується .  

Оскільки крокова траєкторія формується вертикальними та діагональними приростами, то можна заключити, що в вектора приріст DY більший за приріст DХ.  

При додатному знаку оцінювальної функції виконується вертикальний крок, а при від`ємному – діагональний. За умовою задачі знак оцінювальної функції змінюється в кожному інтерполяційному такті, тобто за кожним вертикальним кроком формується діагональний і навпаки.  

Оскільки діагональний крок включає приріст по осі Y, то можна заключити , що на кожне переміщення по осі Х приходиться два переміщення по осі Y, тобто ∆Y=2∆Х.  

Оскільки адреси пікселів при формуванні вектору зменшуються, то це означає, що він формується в напрямку до початкової точки екрану.  

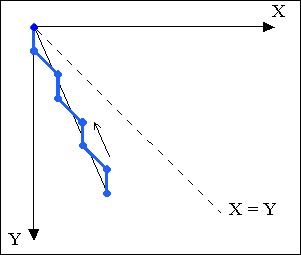           Рис.9.3.  

4.   Довести, що максимальна похибка алгоритмів лінійної інтерполяції з восьмивекторним направленням крокових приростів не може бути меншою половини кроку дискретизації  

Крокова траєкторія, яка формується алгоритмами з восьмивекторним направленням крокових приростів , включає горизонтальні, вертикальні та діагональні прирости, що дозволяє вибрати найближчі точки решітки по відношенню до ідеального відрізка прямої.  

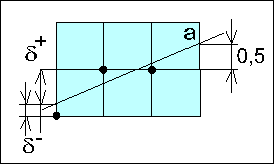          Рис. 9.4.    

Відрізок прямої має по відношенню до найближчих точок решітки дискретного простору дві похибки: d⁺ і d^– (рис. 9.4). З двох можливих точок решітки, одна з яких знаходиться вище, а друга – нижче відрізка прямої, доцільно вибрати ту, для якої похибка d⁺ чи d^– менша по модулю.  

В випадку (а), коли ідеальний відрізок прямої проходить через середину дискрети, то d⁺=|d^–|=0.5, тому найближча точка решітки віддалена від вектору на 0,5 кроку дискретизації. В цьому випадку маємо два ідентичних варіанти вибору найближчих точок решітки , які найближче знаходяться до відрізка прямої. Кожна з цих точок віддалена від відрізка на половину кроку дискретизації.  

Приведений приклад показує, що досягти меншої похибки в цьому випадку неможливо, тому максимальна похибка алгоритмів лінійної інтерполяції не може бути меншою половини кроку дискретизації.  

5.   Визначити значення оцінювальної функції в точці (6,2) при формуванні відрізка прямої згідно алгоритму Пєтуха, Обідника при умові , що∆х=8, ∆y=3, х_н=0, у_н=0. 

Згідно умови виконано 4 горизонтальних і 2 діагональних координатних прирости. При формуванні горизонтального кроку значення оцінювальної функції визначається по формулі:

ОФ_i+1 = ОФ_i – МП,  

де МП – менший із приростів. В даному випадку МП=3.  

При При виконанні діагонального кроку:  

ОФ_i+1 = ОФ_i + D, где D=БП–МП,   D=5. 

Підсумовуючи вказане, знаходимо      ОФ₆ = ОФ₀ – 4МП + 2D.  

Для алгоритму Пєтуха, Обідника ОФ₀=⌊БП/2⌋=4. Враховуючи початкове значення оцінювальної функції знаходимо   

ОФ₆ = 4 – 12 + 10 = 2.  

6.   Визначте тип вектору, який згідно алгоритмулінійної інтерполяції Пєтуха А.М., Обідника Д.Т., має всі значення останньої, рівні початковому значенню.

Оцінювальна функція обчислюється згідно слідуючих формул:    

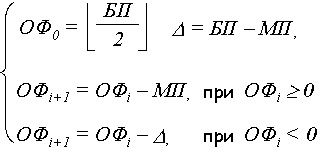
де МП і БП – відповідно менший та більший прирости відрізка прямої.  

Оскільки початкове значення оцінювальної функції завжди більше нуля, то  

ОФ₁ = ОФ₀ – МП.  

При   МП = 0, ОФ₁ = ОФ₀ = ОФ_і,   i = 1,БП.  

7.   Довести, що початкове та кінцеве значення оцінювальної функції при формуванні вектора за алгоритмомлінійної інтерполяції Пєтуха-Обідника рівні.  

&Оцінювальна функція розраховується згідно формул :    

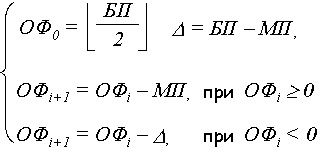
де МП, БП – відповідно менший та більший прирости.  

При ОФ_і≥0 формується горизонтальний (вертикальний) крок, а при ОФ_і<0 діагональний. Кількість діагональних кроків дорівнює МП, а кількість горизонтальних (вертикальних) БП-МП. Оскільки виконується БП інтерполяційних тактів, кінцеве значення оцінювальної функції дорівнює :  

ОФ_к = ОФ_БП = ОФ₀–МП•(БП–МП)+D•МП = ОФ₀–МП•D+МП•D = ОФ₀.  

8.   Визначити мінімальну кількість інтерполяційних тактів алгоритмів лінійної інтерполяції з восьмивекторним направленням крокових приростів.  

Формування крокової траєкторії згідно вказаних алгоритмів здійснюється горизонтальними (вертикальними) та діагональними кроками. Діагональний крок включає в себе одночасне переміщення по обом координатам. При ∆х>∆y крокова траєкторія складається з горизонтальних та діагональних приростів. Враховуючи, що діагональний крок включає переміщення в горизонтальному напрямку, заключаємо що кількість кроків для досягнення кінцевої точки дорівнює ∆x.   

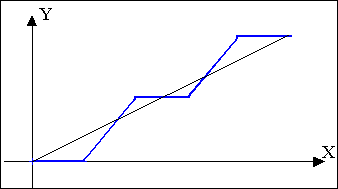         Рис.9.5.    

Аналогічно можна показати, що при ∆y>∆x необхідно виконати ∆y кроків. Таким чином кількість інтерполяційних тактів для алгоритмів з восьмивекторною орієнтацією крокових приростів дорівнює більшому приросту.  

9.   Розробити структурну схему лінійного інтерполятора , який формує крокову траєкторію по методу оцінювальної функції. 

В якості базового алгоритму використаємо алгоритм оцінювальної функції, згідно якого виконуються наступні дії:    

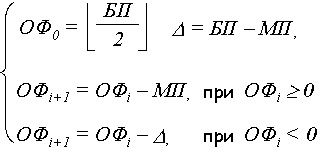
де БП, МП – відповідно більший та менший прирости.  

Цикл інтерполювання закінчується через БП тактів.  

В регістр БП та МП зі вхідної шини D заносяться відповідно більший (БП) та менший (МП) прирости. Регістр накопичуючого суматору обнуляють. Значення БП заноситься в RG накопичуючого суматору (утворений комбінаційним суматором Sm та регістром RG). Через мультиплексор МХ на вхід накопичуючого суматору подається значення МП в інверсному коді (оскільки операція віднімання для даного випадку виконується в доповняльному коді, то при її реалізації на вхід переносу накопичуючого суматору подається рівень логічної одиниці). Значення БП-МП з виходу суматору Sm заноситься в регістр Δ. В лічильник СТ2 з виходу регістра БП подається значення більшого приросту, яке під дією сигналу У₄ записується в лічильник. В регістр RG накопичуючого суматору подається значення [БП/2], яке отримуємо монтажним шляхом на виході лічильника СТ2. На цьому закінчується цикл підготовки.  

В циклі інтерполяції в кожному такті знаходиться значення оцінювальної функції. Для цього на вхід накопичуючого суматору з виходу мультиплексора подається значення D або МП.  

Знак оцінювальної функції визначає сигнал переносу Р_вых суматора. З кожним інтерполяційним тактом значення лічильника зменшується на 1. При досягненні лічильником нульового стану процес інтерполяції закінчують.    

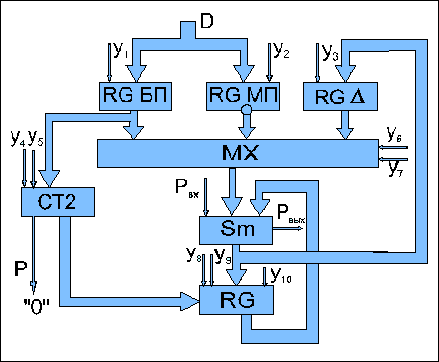   Рис. 9.6.

10.    Визначити значення інтенсивностей кольору точок для забезпечення антиаліайзингу векторної границі з приростами DХ=5, DВ=2 при умові, що інтенсивність кольору I=10

Коефіцієнт похилу вектору дорівнює DY/DX. Задамо кут нахилу відношен- ням I/I_X, тобто DY/DX=I/I_X.    

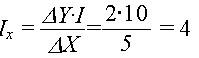
Таким чином, І_Х=4, I=10.  

Виконаємо інтерполювання з параметрами I, І_Х при кількості інтерполяційних тактів DХ=5. При додатньому знаці оціночної фугкції значенння інтенсивності кольорц визначається як різниця між параметрами I і поточним значенням оціночної функції, а при від'ємному – як модуль ОФ.  

БП = 10,   МП = 4  

ОФ₀ = [БП/2] = 5;         D = БП – МП = 6  

ОФ₁ = ОФ₀ – МП = 5 – 4 = 1,     I₁ = I – ОФ₁ = 9  

ОФ₂ = ОФ₁ – МП = 1 – 4 = –3,   I₂ = 3  

ОФ₃ = ОФ₂ + D = –3 + 6 = 3,      I₃ = 10 – 3 = 7  

ОФ₄ = ОФ₃ – МП = 3 – 4 = –1,   I₄ = 1  

ОФ₅ = ОФ₄ + D = –1 + 6 = 5,     I₅ = 5  

Встановленням І₀=5, І₁=9, І₂=3, І₃=7, І₄=1, І₅=5 забезпечує згладження ступінчатої форми вектора.  

11.   Визначити кількість інтерполяційних тактів для формування траєкторії кола ортогональними кроковими приростами.  

Розглянемо перший квадрат ( рис. 9.7 ). Крокова траєкторія формується горизонтальними та вертикальними елементарними переміщеннями.    

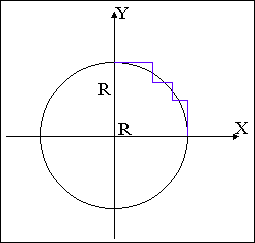          Рис. 9.7.    

Кількість крокових приростів в напрямку координат Х дорівнює радіусу R, оскільки вертикальні кроки не забезпечують переміщення по осі абсцис. Аналогічна ситуація має місце є для ординатного напрямку. Таким чином, кількість крокових приростів для формування траєкторії в першому квадраті дорівнює 2 R, а для всього кола: 2R•4=8R.  

     Зміст