Задачний практикум 

Частина 2 

12.   Визначити п'ять точок траєкторії дуги кола, яка починається з точки (6,0) при умові, що інтерполювання здійснюється по методу оцінювальної функції проти часової стрілки, а радіус кола дорівнює 6.  

Оскільки інтерполювання здійснюється проти часової стрілки, то координати Х точок траєкторії буде зменшуватись, а координати Y – збільшуватись (рис.9.8).   

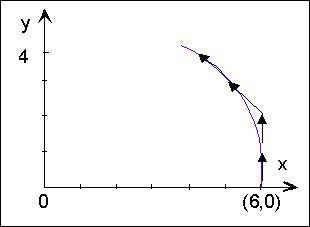     Рис. 9.8.    

Формули для розрахунку оцінювальної функції мають вид:    

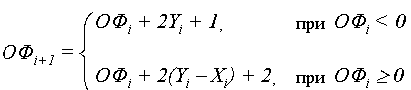
ОФ₀ = –R        ОФ₀ = –6

ОФ₁ = –6 + 2•0 + 1 = –5  

ОФ₂ = –5 + 2•1 + 1 = –2  

ОФ₃ = –2 + 2•2 + 1 = +3  

ОФ₄ = 3+ 2•(3 – 5) + 2 = +5  

Згідно знаків оцінювальної функції заключаємо, що в перших двох тактах формуються вертикальні кроки, а в двох наступних – діагональні. Початкова точка дуги має координати (6,0).  

13.   Визначити та обгрунтувати напрямки траєкторії в режимі доведення в кінцеву точку дуги .  

В першому секторі (рис.9.9,а) крокова траєкторія формується горизонтальними та діагональними (комбінованими) кроковими приростами.    

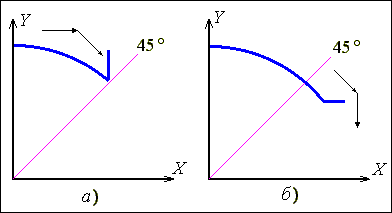         Рис. 9.9.    

Враховуючи, що діагональний приріст включає переміщення по осі Х, то можна констатувати, що всі елементарні кроки до точки Х=У включають переміщення по осі абсцис.  

Звідки випливає, що при формуванні траєкторії гарантовано буде досягнуто координату Х_K, а доведення буде необхідне до координати Y.

Аналогічно можна показати, що при формуванні дуги в другому секторі доведенню підлягає координата Х_K.  

14.   Розрахувати 4 крокові прирости для параболи Y=2X² по методу оцінювальної функції.

Оцінювальна функція визначається по формулі: ОФ_і=y–2x_і²    

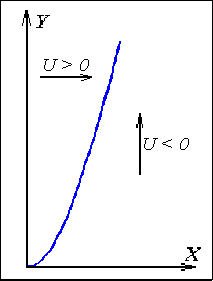       Рис. 9.10.    

При ОФ≥0 виконується крок по осі Х, а при ОФ<0 по осі Y. Після кроку по осі X нове значення х_і+1=х_i+1.  

Тоді ОФ_і+1 = у_i – 2•(х_i+1)² = у_i – 2•х_і² – 2•х_i + 2 = у_i – 4х_і – 2.  

При виконанні кроку по осі Y ове значення аргументу буде розраховуватись як у_і=у_і+1.  

Тоді ОФ_і+1 = у_і + 1 – 2•х_і² = ОФ_і + 1.  

Розрахуємо 4 крокові прирости при умові, що ОФ₀ = 0.  

1. ОФ₁ = 0 – 4 – 2 = –6,    у = 0,      х = 1.  

2. ОФ₂ = –6 + 1 = –5,       у = 1,      х = 1.  

3. ОФ₃ = –5 + 1 = –4,       у = 2,      х = 1.  

4. ОФ₄ = –4 + 1 = –3,       у = 3,      х = 1.  

15.Привести вираз для кривої Ерміта, початкова та кінцева точки якої мають координати (0,g), (1,b), а похідні в початковій та кінцевій точці відповідно рівні a, g.

Кубічна крива в формі Ерміта задається рівнянням:  

х(t) = at³ + bt² +ct +d.  

Знайдемо значення невідомих а, b, с, d.  

x(0) = d, x(1) = a + b + c + d,      x'(0) = c, x'(1) = 3a + 2b + c.  

Таким чином:  

x(0) = d,          x(1) = a + b + c + d,  

x'(0) = c,       x'(1) = 3a + 2b + c.  

Розв'язок системи дає невідомі а, b, с, d.  

16.   Визначити геометричний вектор Безьє для кривої X(t)=3t³+15t²+4t+1 при умові, що Р₂=7, Р₃=9.  

Геометричний вектор Безьє має вигляд :    

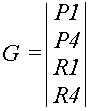
де  Р1 = x(0),  P2 = x(1),  P3 = x'(0), P4 = x'(1).

Підставляючи в x(t) значення 0 та 1, одержимо :   Р1=1,  Р4=23.  

Згідно алгоритму Безьє значення R1 і R4 визначаємо по формулах

R1 = 3•(P2 – P1), R4 = 3•(P4 – P3), R1 = 18,  R2 = 42.  

Таким чином геометричний вектор Безье для даного прикладу має вид:    

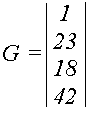
17.   Знайти вираз для поліному Лагранжа при умові, що базові точки мають наступні координати : (7,10), (9,30), (11,50).  

Інтерполяційний поліном Лагранжа n-го степеня для даної множини точок має вигляд:   

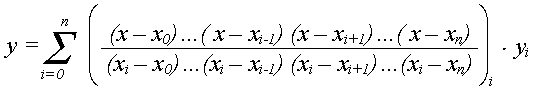
В даному випадку ми маємо:    

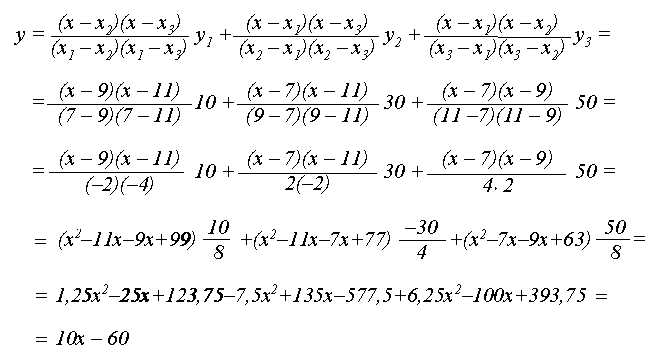
ВВисновок: в даному випадку крива вироджена в відрізок прямої, який проведений через три точки .  

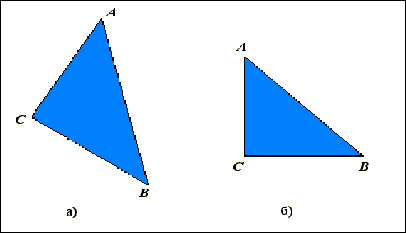
18.   Визначити тип трикутника, який найбільш доцільний для рендерингу Гуро з точки зору обчислювальних затрат та точності розрахунку інтенсивностей кольору пікселей.  

Першим етапом рендерингу Гуро є тріангуляція області, обмеженою полігоном. Зафарбовування виконується від ребер АС і СВ (рис.9.11а)    

     Рис 9.11.    

Якщо відрізок СВ паралельний осі абсцис, то відпадає необхідність в рендерингу нижнього ребра.  

Приріст інтенсивності кольору вздовж ребра АС визначається по функції.   

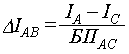
де БП_АС – більший з приростів ребра АС.  

БП_АС=АС при умові, що відрізок АС паралельний осі ординат. Таким чином, найбільш доцільним для рендерингу Гуро є прямокутний трикутник, катети якого паралельні осям координат.  

19.   Виконати опис полігональної сітки, приведеної на рис. 9.12 , згідно методу явного завдання ребер.  

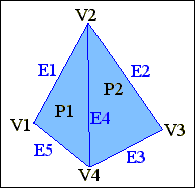         Рис. 9.12  

V = (V₁,V₂,V₃,V₄) = ((X₁,Y₁,Z₁),(X₂,Y₂,Z₂),(X₃,Y₃,Z₃),(X₄,Y₄,Z₄))  

E₁ = (V₁, V₂, P₁, L)       E₃ = (V₃, V₄, P₂, L)  

E₂ = (V₂, V₃, P₂, L)       E₄ = (V₁, V₂, P₁, P₂)  

P₁ = (E₁, E₄, E₅)           P₁ = (E₁, E₄, E₅) 

Метод забезпечує швидкий пошук спільних ребер, виключає дублювання вершин при завданні багатокутників.  

20.   Виконати опис полігональної сітки, зображеної на рисунку 9.13, шляхом явного завдання багатокутників і з використанням покажчиків.  

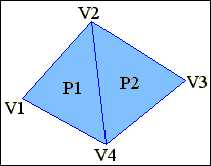                Рис. 9.13.    

Опис полігональної сітки при явному завданні багатокутників має вигляд:  

Р₁ = (V₁,V₂,V₄) = (( X1,Y1,Z1), ( X2,Y2,Z2),…(X₄,Y₄,Z₄))  

Р₂ = (V₂,V₃,V₄) = (( X2,Y2,Z2), ( X3,Y3,Z3),…(X₄,Y₄,Z₄))  

Явне завдання багатокутників характеризується надлишковістю, оскільки для вершин V2 і V4 опис проведений двічі.  

Опис логічної сітки при використанні покажчиків має вид:  

Р₁ = (V1,V2,V3,V4) = ((X1,Y1,Z1),(X2,Y2,Z2),(X3,Y3,Z3),(X4,Y4,Z4))  

Р = (1,2,4)          Р = (4,2,3)  

При завданні Р цифр в дужках – є покажчики вершин в описі V.  

21.   Виконати відсікання відрізка прямої, представленого на рисунку 9.14 , згідно алгоритму ділення відрізка пополам.  

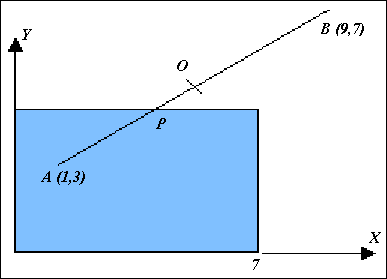         Рис. 9.14.    

Знаходимо координати точки О.    

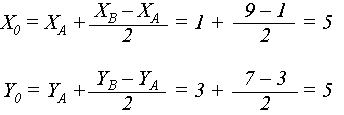
Відрізок ОВ згідно алгоритму Коена-Сазерленда відкидається.  

Знаходимо координати точки Р.    

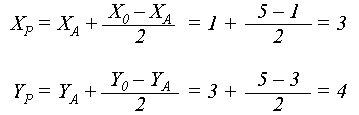
Відрізок ОР згідно алгоритму Коена-Сазерленда відкидається.  

Відрізок АР АР належить вікну.  

22.   Виконати відсікання відрізків прямих, зображених на рисунку 9.15, згідно алгоритму Коена-Сазерленда.    

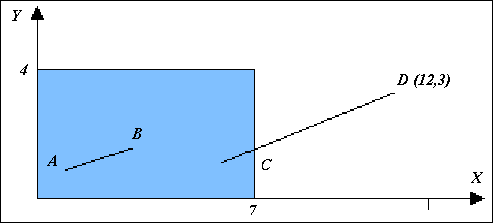       Рис. 9.15.    

Визначимо чотирьохрозрядні коди для точок А та В згідно слідуючих ознак:

Оскільки чотирьохрозрядні коди точок А і В нульові, то відрізок знаходиться всередині вікна.  

Для точок С і Д чотирьохрозрядні коди дорівнюють: точка С – 0000, точка Д – 0001.  

Оскільки операція порозрядного логічного добутку дає нульовий результат, то необхідно виконати відсікання.  

Відрізок прямої СД задаємо рівнянням виду:   

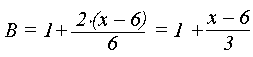
&Максимальна абсциса границі вікна дорівнює 7. Знаходимо Y для х=7.   

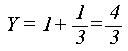
Точка О має координати (7,4/3). Відрізок ОД відкидається.  

23.   Визначити мінімальний об’єм відеопам’яті режиму True Color, якщо монітор підтримує стандарт Artist 1+.  

Режим True Color забезпечує 16777216 кольорів, що вимагає використання log₂16777216=24 розрядів відеопам`яті на один піксель.  

Розмір адресного простору для режиму Artist 1+ дорівнює 1024х768, а загальна кількість точок на екрані в цьому випадку дорівнює 1024*768=786432.  

Необхідний об`єм відеомам`яті для режиму True Color буде дорівнювати 786432*24=18874368 біт.

24.   Визначити мінімальний об’єм відеопамяті при умові, що підтримується режим SVGA і формується 256 кольорів.  

Режиму SVGA відповідає екран з адресним простором 1024*768 точок.  

Для кодування 256 кольорів необхідно √256=8 шарів пам’яті. Загальний об’єм пам’яті буде рівний:

1024*768*8 = 6`291`456 бит.  

25.   Визначити частоту рядкової розгортки при формуванні телевізійного растра з числом рядків у кадрі Z=625 при: (а) прогресивній (б) черезрядковій розгортці.  

Відповідно до формули F_z=Z*f_k визначаємо для прогресивної розгортки (f_k=50 Гц) f_z=625*50=31250 Гц; для черезстрочной развертки (f_k=25 Гц) f_z=625*25=15`625 Гц.  

26. Визначити кількість пікселів зображення, яку можливо сформувати при асинхронній растровій розгортці за 50 кадрів при умові, що зворотній хід рядка та кадру відповідно рівні t_p, t_k, час розрахунку піксела мікропроцесором – t, а кількість рядків на екрані – n.  

При асинхронній растровій розгортці відеопам’ять доступна під час зворотних ходів рядка та кадра. За час зворотнього ходу рядка можливо сформувати ⌊t_p/t⌋ пікселів. Враховуючи, що кількість рядків дорівнює n, то за прямий хід кадра буде сформовано ⌊t_p/t⌋•n ікселів. За час зворотного ходу кадра мікропроцесор сформує ⌊t_k/t⌋ точок. За 50 кадрів загальну кількість точок визначаємо по формулі: 50(n•⌊t_p/t⌋+⌊t_k/t⌋).  

27.   Визначити кількість оптоелектроних пар передекраної сенсорної панелі для забезпечення режиму точного позиціювання при умові, що використовується екран стандарту Artist 1+.  

Передекранна сенсорна панель включає пари оптоелектроних елементів, які розміщені по периметру екрану. Кожна з таких пар включає джерело світла та його приймач.  

При дотиці оператором передєкранної панелі виконується введення в ЕОМ координат Х і Y положення об’єкта на екрані.

Режиму Artist 1+ відповідає адресний простір 1024х768 точок.  

Позначимо через n – кількість оптоелектроних пар, яку необхідно забезпечити для однієї з сторін екрану, яка включає N точок.  

Тоді N/n – визначає розмір макрозони для режиму позиціювання.  

Для забезпечення ідентифікації кожної точки макрозони відношення N/n повинно дорівнювати n, тобто N/n=n. N=n².  

Звідси n=√N. При N=1024, n=32. Якщо N=68, n=29.  

28.   Визначити типи чотирикутників, для яких при заповненні по критерію зв’язності необхідно дві точки-затравки при умові, що виконується горизонтальна растеризація, а одна з точок-затравок розміщена в верхньому куту чотирихкутника.  

Більш як 2 очки -затравки необхідно при умові, що багатокутник не є випуклим.

Можливі варіанти невипуклих чотирикутників приведені на рис.9.16.  

Як видно з рисунка точки затравки при горизонтальній растеризації необхідно для випадків А і С.   

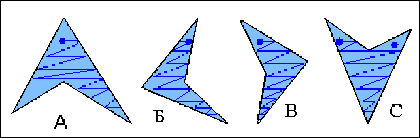       Рис. 9.16.  

     Зміст