Зміст           Наступна сторінка          Електронні посібники ВНТУ

1  МАТЕМАТИЧНІ ОСНОВИ ТЕОРІЇ АВТОМАТИЧНОГО УПРАВЛІННЯ

1.1 Основні поняття та терміни

1.2 Історія ТАУ

1.3 Приклади об’єктів та систем автоматичного управління

1.4 Склад типової САУ

1.5 Фундаментальні принципи управління

1.6 Динамічні системи

1.7 Лінеаризація. Метод малих збурень

1.1 Основні поняття та терміни

Термін “керування” (вживається також “управління”) охоплює надзвичайно широке коло понять, що викликано різною природою об’єктів, наприклад керування технологічним процесом, підприємством чи державою. Крім того, під керуванням (управлінням) розуміють також командування військами, керування транспортними засобами (судном, літаком, автомобілем), диригування оркестром і інша. З цієї точки зору ТАУ – частина кібернетики, яка вивчає процеси використання інформації і управління в системах різної фізичної природи.

Автоматизація виробництва – один з важливих факторів науково-технічного процесу, за рахунок якої відбувається інтенсифікація процесів випуску продукції та зменшення витрат енергетичних та матеріальних ресурсів. Сучасні системи керування мають складну багаторівневу (ієрархічну) структуру, в якій використовуються обчислювальні мережі різного рівня на основі ЕОМ та мікропроцесорних засобів.

В даних текстах лекцій розглядаються локальні системи автоматичного регулювання, які призначені для підтримання необхідних технологічних режимів, які характеризуються певним набором значень технологічних змінних – температури, рівня, тиску, концентрації і інш. Розглядаються також питання оптимізації технологічних режимів, а також можливості пристосування (адаптації) систем до змінюваних умов роботи. Для складних технологічних об’єктів розробляються системи керування, які також мають достатньо складну структуру і розвинені зв’язки між окремими частинами(елементами).

Автоматика – технічна наука, яка розробляє принципи побудови автоматичних систем та необхідних для них засобів, методи аналізу і синтезу цих систем.

Керування технічним процесом – цілеспрямована діяльність, направлена на досягнення бажаних результатів (отримання прибутку, мінімальної собівартості продукції, забезпечення її якості) на основі отримання та обробки інформації про стан об’єкта та умови його роботи. В процесі керування виконується ряд операцій, які відповідають таким етапам :

– збирання інформації про стан об’єкта та зовнішнє середовище;

– аналіз та обробка інформації;

– прийняття рішень на основі необхідної інформації;

– реалізація керуючих діянь за допомогою технічних засобів.

Виконання цих операцій забезпечує автоматичний контроль процесу, пуск та зупинку технологічних агрегатів, підтримання необхідних режимів при виконанні вимог надійності та стійкості.

Система автоматичного управління (керування) – сукупність об’єкта та автоматичного пристрою керування.

Автоматизована система керування передбачає участь у формуванні керуючих дій людини (особи, яка приймає рішення - ОПР). Автоматизовані системи створюються для складних об’єктів, де участь людини в прийнятті рішень є визначальною, а для цього необхідно отримати та переробити великі масиви інформації.

Автоматичні системи забезпечують виконання всіх функцій керування без участі людини (автоматично), але для обслуговування, ремонту та налагодження потрібні кваліфіковані спеціалісти.

Автоматичні системи регулювання (АСР) – сукупність об’єкта та пристрою керування (автоматичного регулятора), процес функціонування яких характеризується тим, що відомі задані значення регульованих координат.

Об’єкт керування (регулювання, автоматизації, керований об’єкт) – технологічний процес, агрегат або комплекс, призначений для здійснення впливу на сировину, матеріали для отримання продукту чи напівпродукту. В складних системах керування об’єктом може бути виробництво, підприємство, галузь промисловості. В будь-якому випадку для досягнення мети функціонування необхідно сформувати керуючі дії, які компенсують небажані відхилення від обраного режиму. Зрозуміло, що об’єкти можуть бути різної природи, мають різне призначення, виконувати різні функції. В той же час система керування створюється саме для об’єкта, тому його властивості визначають основні характеристики системи керування – її структуру, функції, показники стійкості та якості. Таким чином, саме об’єкт визначає призначення системи керування, наприклад : автоматизована система керування підприємством, автоматична система керування випарною установкою, автоматична система регулювання температури і т.д.

1.2 Історія ТАУ

Перші пристрої автоматичного управління – самостріли, водяні та повітряні двигуни, з’явились багато тисячоліть тому. Математичні елементи – диференціальні рівняння – кілька століть тому, але теорія саме автоматичного управління – не більше 100-130 років.

Перші праці (Раус, Гурвиць, Ляпунов, Вишнеградський, …) були пов’язані з розробкою регуляторів частоти обертання парових машин, парових турбін, електродвигунів (1860-1900 роки).

Саме тоді інженери захотіли не підбирати, а розраховувати параметри регуляторів так, щоб САУ була стійкою, точною, швидкодіючою.

Далі областями застосування САУ були виробничі процеси (регулювання: температури, тиску, рівня, концентрації – всього, що можливо вимірювати і чим, зрозуміло, можна управляти, для чого і були отримані математичні моделі). З’явились авторульові автопілоти.

З 30-х років почались прикладні праці по ракетній техніці – ракета, на відміну від літака без САУ зовсім нестійка.

З тих пір системи озброєння – керовані ракети, танкові приціли, бомбові,…, системи посадок, взльоту, стиковки, … і т.д. стали традиційною областю застосування передових технічних і програмно-математичних методів управління.

Починаючи з 1970-х років з’являється нова область застосування САУ – станки з числовим програмним управлінням, роботи. Причому, роботу потрібно було не підтримувати температуру чи швидкість, а встановлювати колесо автомобіля на рухомому конвеєрі, заливши герметиком по контуру складне по формі скло автомобіля.

Відомі системи запалювання і вприску палива, які забезпечують мінімальні витрати пального. Найбільш масові регулятори в розвинених країнах – це регулятори в пральних машинах, тостерах, плитах, кондиціонерах і, найголовніше, в опалювальних системах.

1.3 Приклади об’єктів та систем автоматичного управління

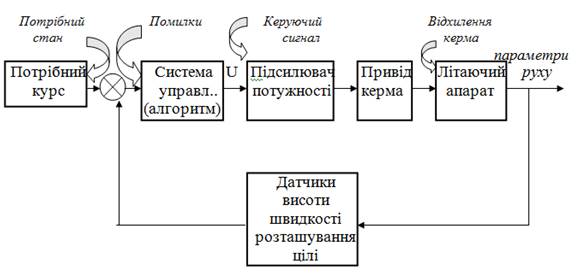
ПРИКЛАД 1: Крилата ракета

На рис. 1.1 представлений безпілотний літак з 0,5 т вибухівки; точність наведення до сантиметрів, може поцілити в замок на воротах ангара, у вентиляційну шахту.

Літає, зазвичай, на висоті 40-200м, використовуючи канави, русла для маскування дальності польоту 1000-5000 км.

 

 

ПРИКЛАД 2: Терморегулятор устаткування для обробки напівпровідникових пластин

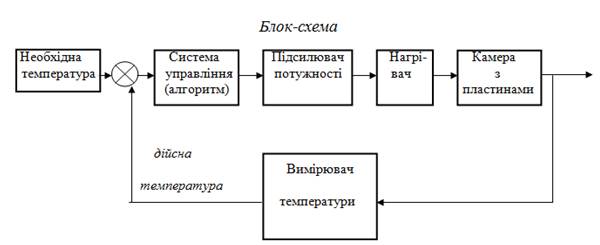
Якість пластин суттєво залежить від температури. Необхідна точність ⁰С. На неіснуючому ВО ”ЖОВТЕНЬ” мікросхеми температури регулювалися вручну. Рівень браку – 70-80 %. В Японії на такому ж виробництві – 0,3 %, в США – 3%.

ПРИКЛАД 3:

Системам автоматичного управління доручають: управляти нафтокомбінатом, енергосистемою, великим літаком, атомною електростанцією. Відмови в таких системах безцінні. Якою повинна бути ідеальна система для таких випадків? Розглянемо два приклади.

На рис. 1.4 наведена звичайна схема аварійного гасіння реактора при відсутності охолоджуючої води.

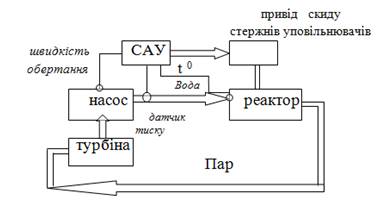
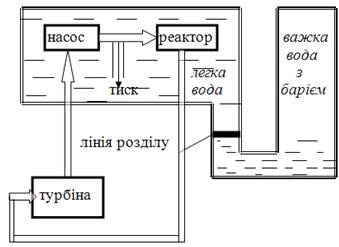
На рис. 1.5 наведена аварійна система (Швеція), яка не має датчиків і приводів. При падінні тиску в магістралі просто більш густа вода з солями барію витісняє воду та глушить і охолоджує реактор. Ідеальна САУ повинна бути звичайним механізмом, не мати цих самих датчиків, підсилювачів, приводів тощо.

ПРИКЛАД 4: Система регулювання приводу лазерного компакт- диску - привід CD-ROM

Всі ви знаєте, що в сучасних масових комп’ютерах, крім звичних пристроїв зовнішньої пам’яті на магнітних дисках, широко використовуються лазерні компакт-диски, першочергово розроблені для звукозапису/відтворення.

До речі, про термінологію: те, що для аудіоплатівок — програвач, те що для магнітних дисків — дисковід, а те, що для лазерних комп’ютерних дисків (КД) —привід.

Сьогодні привід КД коштує 200-800$ і буде дешевшати, диск сам по собі—2-3 $, а ціна його визначається тим, що там записано:

– енциклопедія – 50-100 $;

– ігри – 10-20 $;

– програмна система з документацією – 1000 $.

Стандартна ємність компакт-диска  600 Мбайт. Ширина доріжки 1/200 товщини людської волосини.

Нормально може працювати така система при субмікронній точності позиціонування головки відносно доріжки на диску (мікрон = 0,001 мм).

На відміну від приводу магнітного диску, голівкою зчитування керує не одна, а цілих три САУ:

1)  позиціонування на доріжці;

2)  витримування висоти над доріжкою;

3)  витримування постійної лінійної швидкості переміщення диску під головкою зчитування.

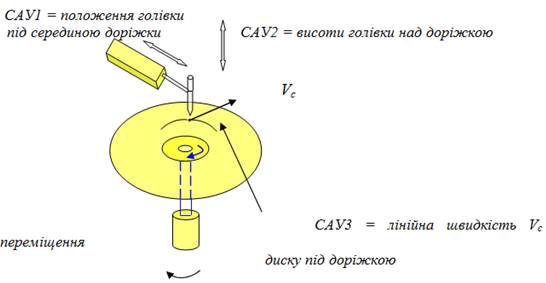
Між іншим, навіщо тут потрібні САУ?

Тому, що диск з’ємний, при обертанні має радіальні та вісьові биття – і щоб голівка читала потрібну доріжку, не розфокусовувалась необхідно на кожному оберті рухати голівку, відстежуючи ці биття.

Саме ці системи були не під силу радянській промисловості.

Сьогодні навіть виробництво обгортки для шоколаду, програвачів – неможливе без високої науки, без високої технології, не в останню чергу – в галузі управління.

ПРИКЛАД 5: Електродвигун постійного струму з незалежним збудженням

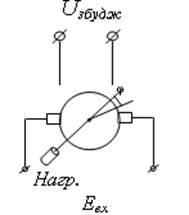
Запишемо рівняння динаміки для ротора двигуна і того, що цей електродвигун переміщує. В якості змінної виберемо кут повороту вала j (1.1)

 

 

(1.1)

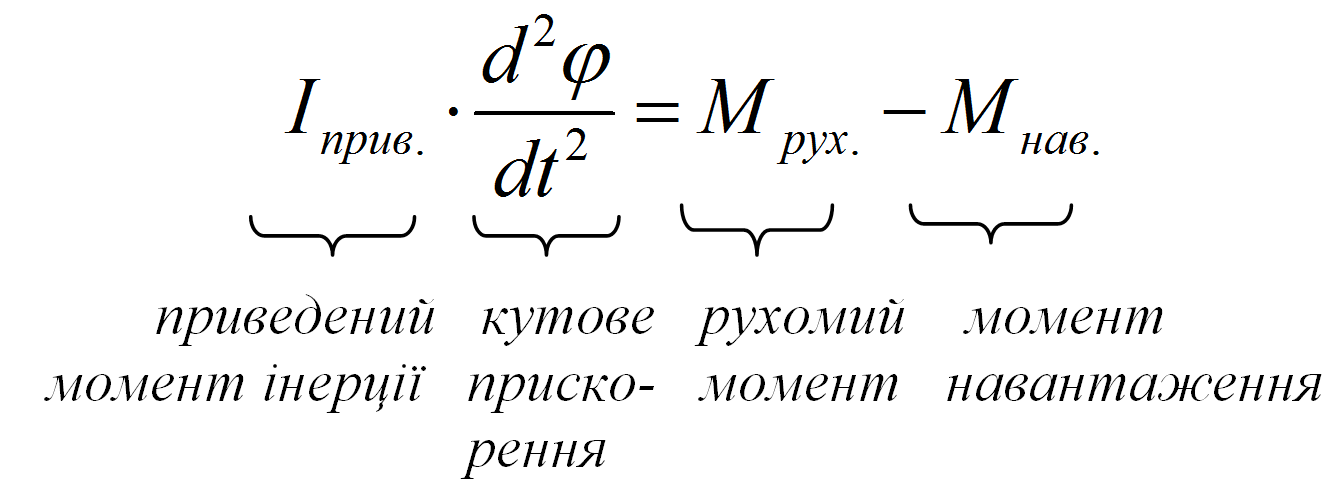
Для електродвигуна постійного струму з незалежним збудженням справедлива залежність:

 

 

(1.2)

 

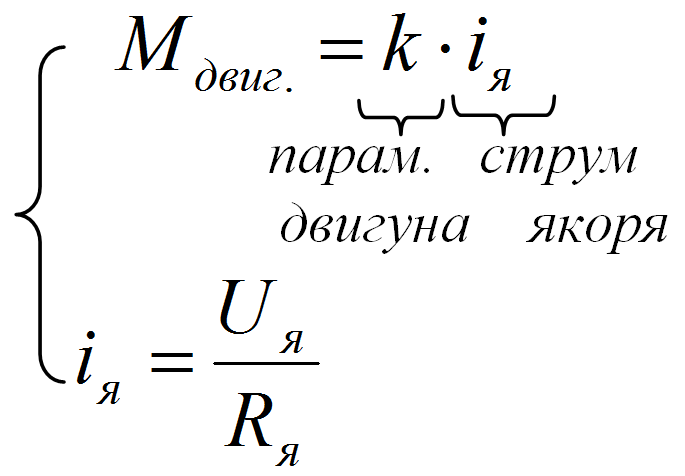
(1.3)

Для кола якоря рівняння Кірхгофа для напруг мають вигляд:

 

(1.4)

 

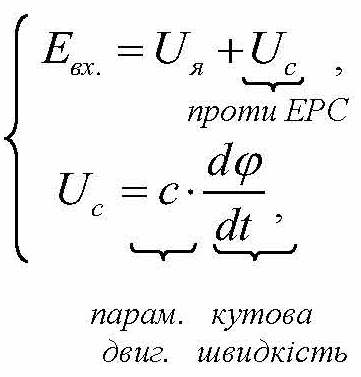
(1.5)

Вирішуючи спільно (1.1)-(1.5) і нехтуючи моментом навантаження М_{навант.}, отримаємо:

 

(1.6)

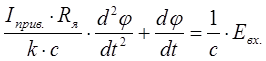
Введемо стандартні позначення:

 

(1.7)

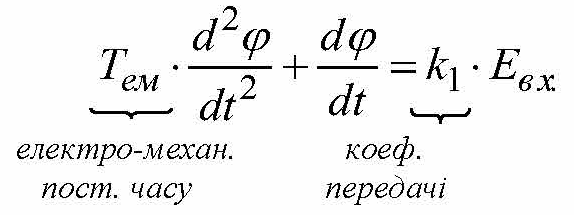
Якщо ввести замість j змінну 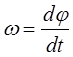 – швидкість  обертання, то маємо:

 

(1.8)

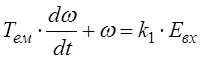
В сталому режимі, 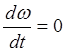, тому:

 

(1.9)

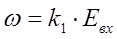
Рівняння (1.8) – рівняння динаміки,  рівняння (1.9) – рівняння статики.

Розглянемо коротко ще декілька класичних об’єктів управління – детальні процедури отримання математичних моделей (ММ) динаміки для цих об’єктів можете знайти в учбових посібниках.

ПРИКЛАД 6: Економіка - динаміка виробництва

Вхід – капіталовкладення:

U₁ – в основні фонди – виробництво станків;

U₂ – в робочу силу та сировину – виробництво шкарпеток.

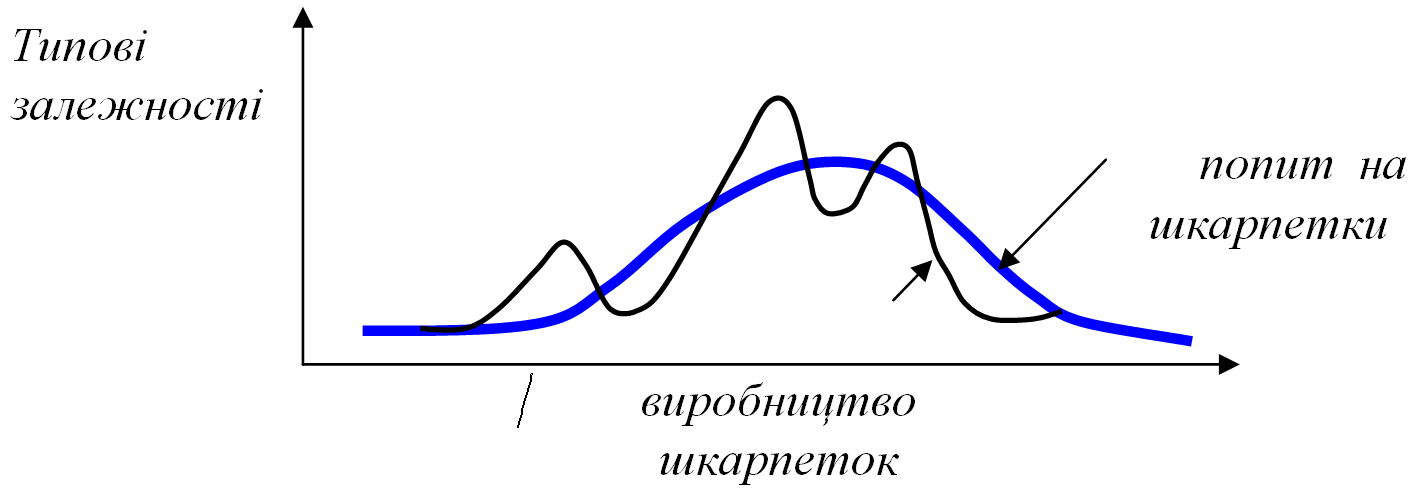
Попередні висновки: підприємство, як і літак, може бути нестійким.

1.4 Склад типової САУ

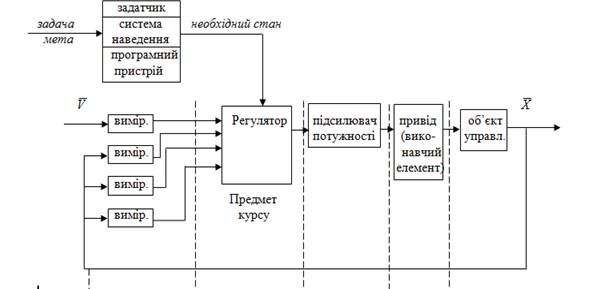
Предметом курсу в основному є вивчення регулятора (аналіз і синтез), все інше при синтезі САУ, як правило задано.

1.5 Фундаментальні принципи управління

1) Принцип програмного управління (закон зміни керованої величини раніше відомий).

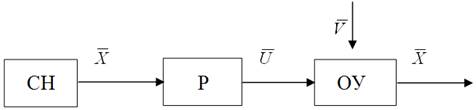
2) Принцип управління по збуренню.

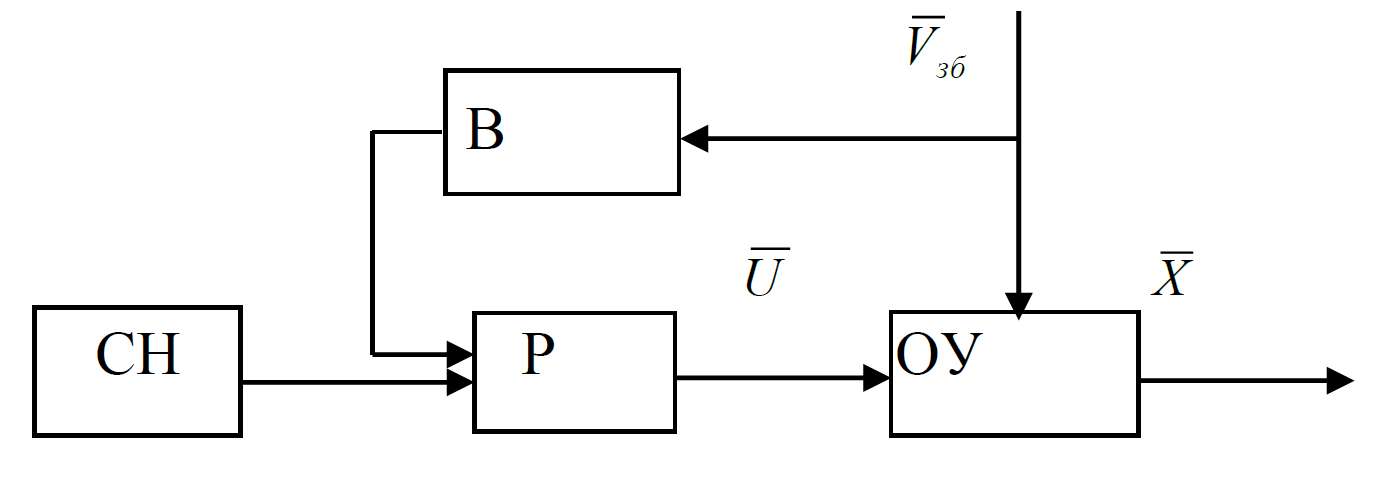
3) Принцип управління по відхиленню (по помилці) – зі зворотнім зв’язком.

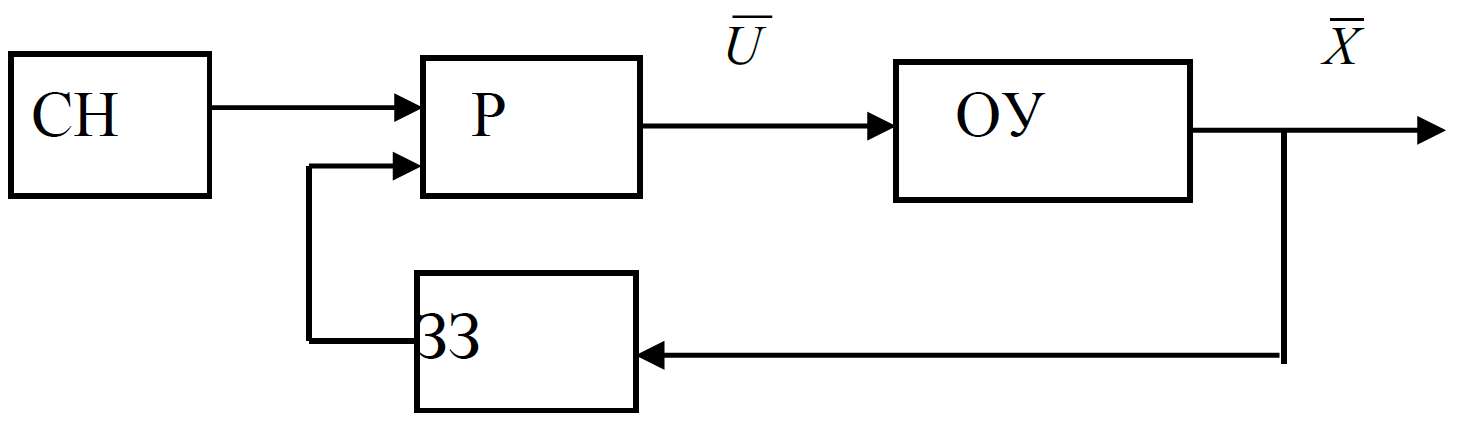
СН – система наведення (програмний пристрій, задавач);

Р – регулятор;

ОУ – об’єкт управління;

ЗЗ – зворотній зв’язок;

В – вимірювач.

В реальних системах можна зустріти всі три типи управління.

1.6 Динамічні системи

Всі об’єкти і системи можуть бути описані в термінах управління, збурення, виходу (стану).

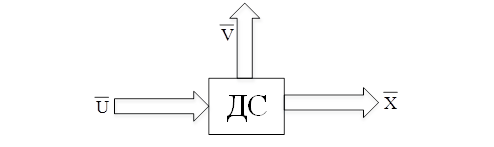
– управління (вхід керуючий)

                           (вектор управління);

– збурення     (вхід обурюючий)

                           (вектор збурення);

– стан            (вихід )

                           (вектор стану).

Більш загальний математичний опис динамічної системи (ДС):

,

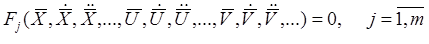де m – кількість рівнянь;

похідні можуть бути будь-якого порядку;

функції можуть бути будь-якого виду, наприклад, .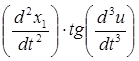

За допомогою нескладних підстановок можемо отримати систему диференціальних рівнянь з похідними не вище першого порядку, наприклад, запишемо рівняння:

, 

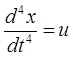чотирма наступними рівняннями:

 

 

Заміна

 

Диф. рівняння

 

 

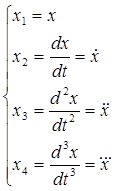
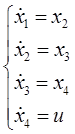
Отже, одне диференціальне рівняння 4-го порядку можемо замінити чотирма рівняннями першого порядку.

В більшості випадків можна вирішити диф. рівняння відносно похідних:

.

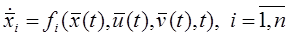Такий вид рівняння називається формою Коші.

Визначення: динамічні системи, в яких коефіцієнти прямо залежать від часу, називаються нестаціонарними.

Найбільш типовий приклад нестаціонарних систем – космічна ракета, маса якої зміниться в польоті в 5-20 раз через вигорання палива і скидання ступенів.

В деяких випадках функції  f_i – лінійні:

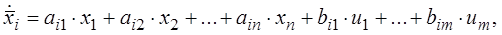
де 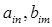  – коефіцієнти.

Для лінійних динамічних систем (ЛДС) існують загальні фундаментальні і потужні методи аналізу і синтезу, а для нелінійних систем таких загальних методів не існує.

    Реальні об’єкти взагалі нелінійні.

Чи можливо так хитро скласти рівняння об’єкта, щоб вони були лінійні? Ваші пропозиції?

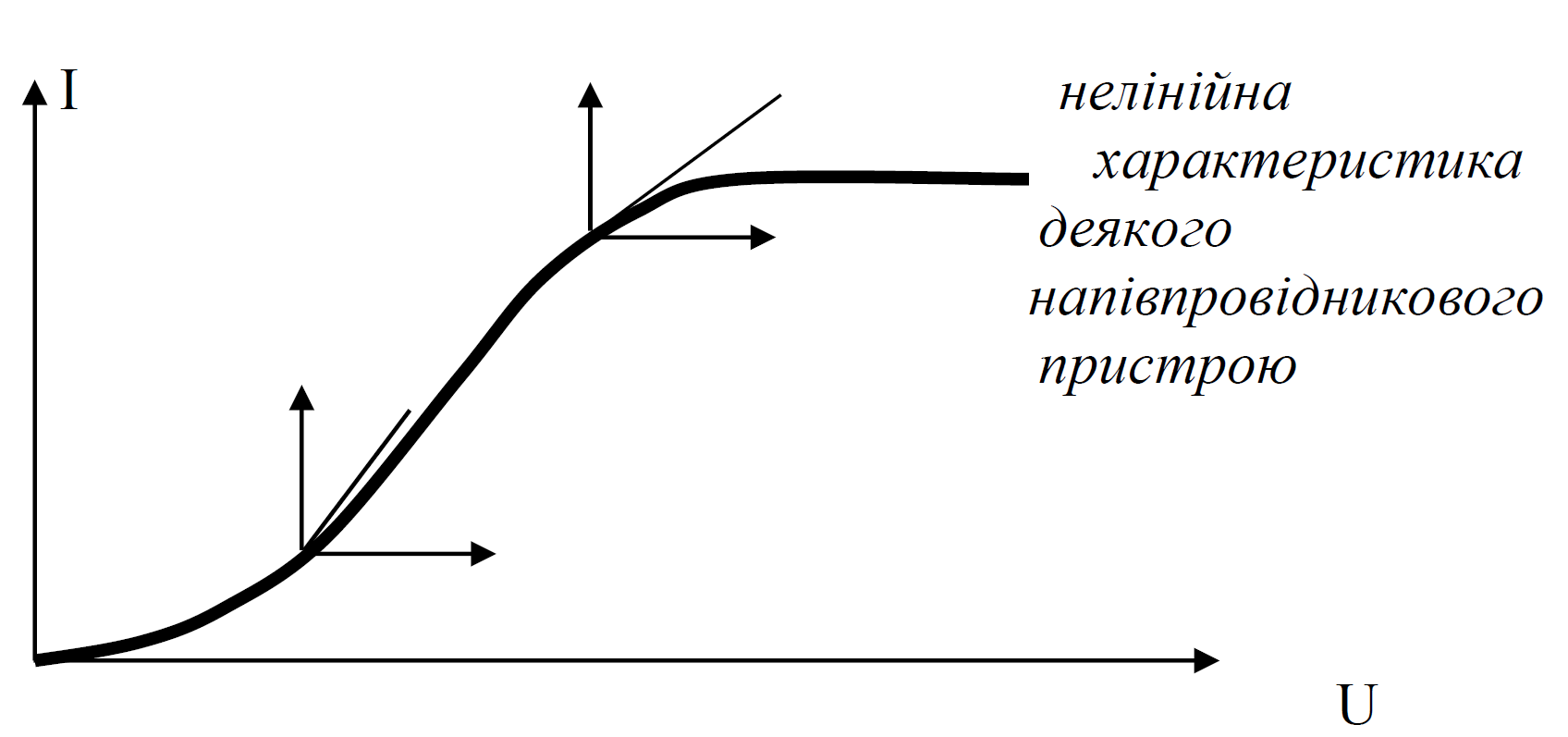
Чи можливо користуватись лінійною залежністю?

Так, якщо вибрати на нелінійній залежності відповідно початок і діапазон вимірювання змінних.

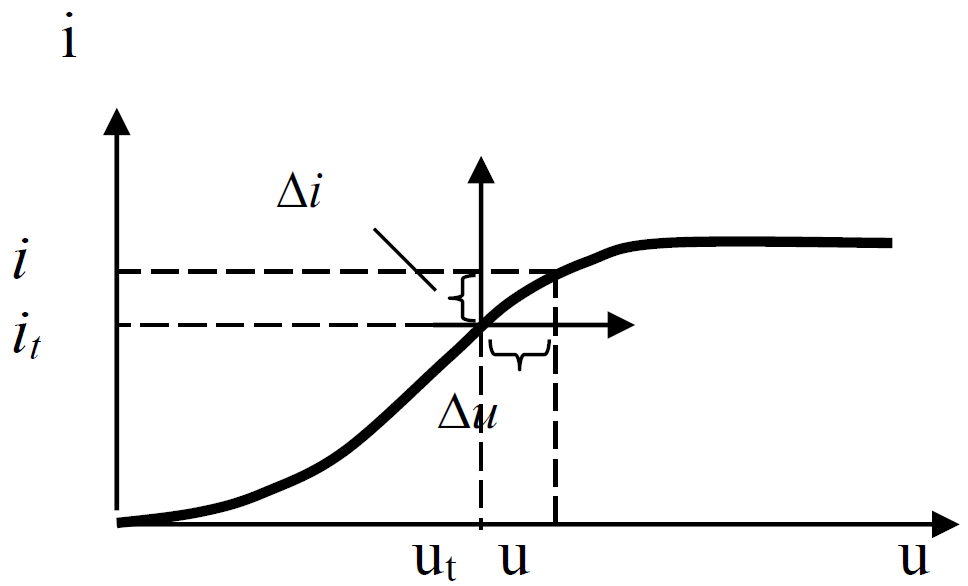
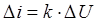         лінійна залежність;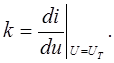      

Процес отримання лінійної математичної моделі з початкової нелінійної називається лінеаризацією.

Розглянемо один з методів лінеаризації нелінійних рівнянь динаміки об’єкта – метод малих збурень.

1.7 Лінеаризація. Метод малих збурень

Обгрунтування  використання методу в задачах аналізу та синтезу САУ.

Добре спроектована САУ повинна підтримувати малі відхилення змінних, які регулюються, відносно знань, які потрібні, а метод малих збурень базується на припущенні про меншості зміни змінних, який дозволяє замінити всі нелінійні залежності наближеними лінійними.

Коротко розглянемо суть методу і приклади лінеаризації.

Дано:

1) 

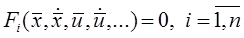
Первісні (загальні) рівняння об’єкту;

2) 

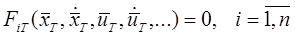
Рівняння об’єкту для режиму, який потрібен (опорного).

Розв’язок:

1) Введемо нові змінні, їх називають “збуреннями” (це джерело плутанини!):

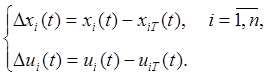
2) Замінимо  і  в початкових рівняннях на 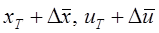, виконаємо алгебраїчні перетворення.

3) Всі нелінійні залежності типу 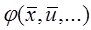 розкладаємо в ступеневі (багатомірні) ряди відносно  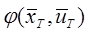по ступеням  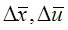і обмежуємося доданками порядку не вище першого, наприклад :

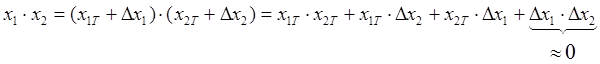
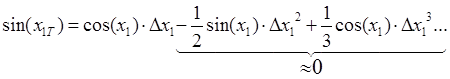
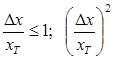– мала величина вищого порядку.

4) Після підстановки і відкидання доданків менше першого порядку меншості, з початкових рівнянь віднімаються відповідні рівняння для опорного режиму, в кінці отримаємо систему лінійних диференціальних рівнянь відносно змінних 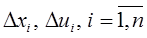, які за термінологією Ляпунова  називаються рівняннями першого наближення.

Коефіцієнти цих рівнянь – певні функції від параметрів і змінних опорного режиму. Вони можуть бути постійними (стаціонарна система) і змінними (нестаціонарна система).

Лінійна частина прирощеної функції – це диференціал. Тому, практично, лінеаризація зводиться до диференціювання початкових рівнянь.

Розглянемо приклад лінеаризації, вважаючи, що U_зб. – змінна управління.

Початкові рівняння:  

                

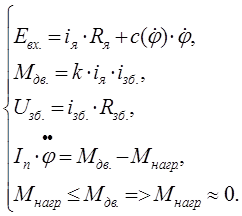
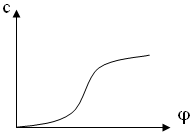
де – нелінійна залежність коефіцієнту, що залежить від конструкції двигуна.

Перетворимо ці рівняння, виключимо проміжні змінні:

;

 

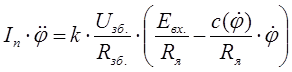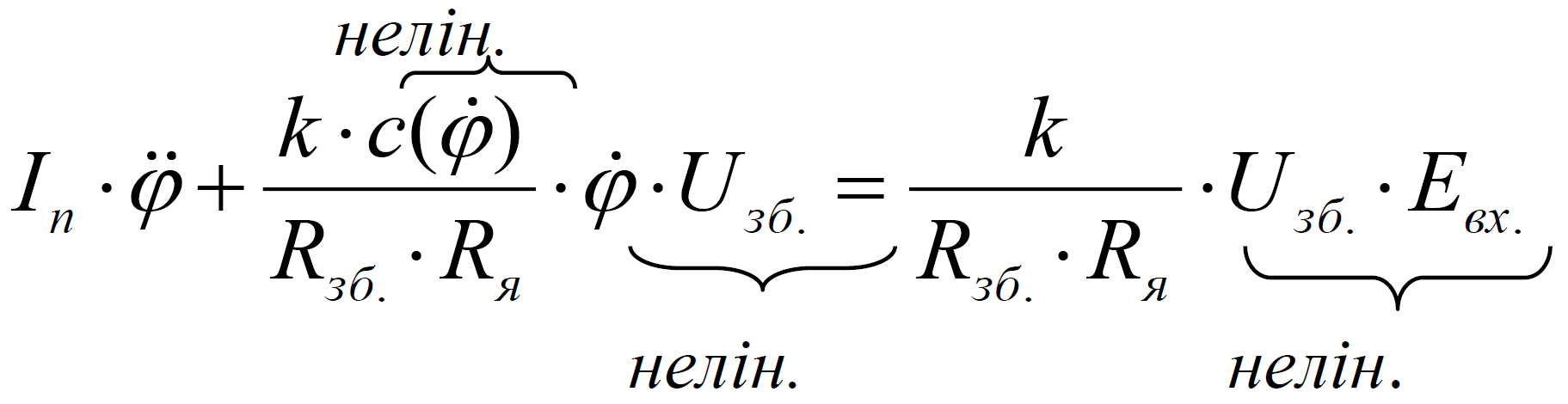
Лінеаризуємо це рівняння – диференціюємо по 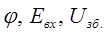 і при всіх змінних без знака диференціала D ставимо індекс Т-опорного руху.

 

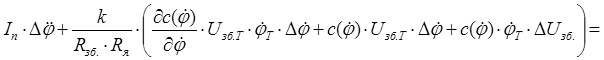
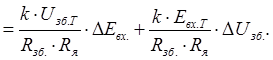
Групуємо, нормуємо:

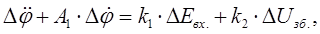
де

 

 

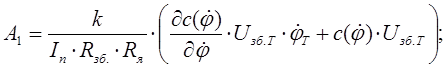
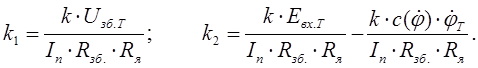
Приведемо до форми Коші, для чого введемо стандартні позначення:

                           

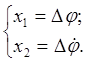
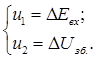
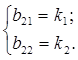
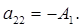
Тоді: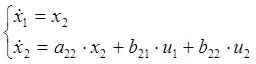                           

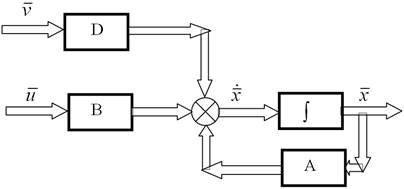
Аналогічно, можливо лінеаризувати будь-який об’єкт і завжди звести лінеаризовані рівняння до канонічної форми:

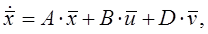
де – вектор  стану; – вектор управління; – вектор збурення;

A, B, D – відповідні матриці; n – кількість змінних стану;

m –  кількість змінних управління; k – кількість змінних збурень.

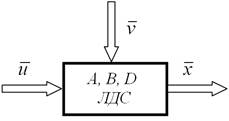
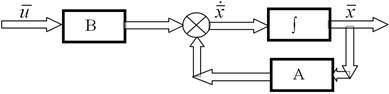
Блок-схемне представлення лінійної динамічної системи :

   

   

   

Контрольні запитання:

1. Дайте визначення поняття “система автоматичного керування ”.
2. В чому полягає процес функціонування системи автоматичного керування?
3. Поясніть основні терміни “система”,”об’єкт”, ”регулятор” і інш.
4. Наведіть приклади класифікації систем автоматичного керування.