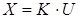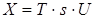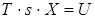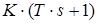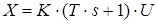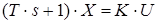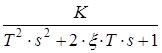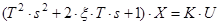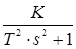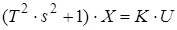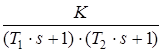Т. М. Боровська. Теорія автоматичного управління. Курс лекцій

Перетворення Лапласа дозволяє замінити ці операції на ділення та множення відповідно. Хевісайд використовував аналогічне перетворення для розв’язку диференціальних рівнянь без чіткого обгрунтування. Пізніше Лаплас дав математичний фундамент для цього перетворення.

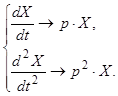
оператор диференціювання Хевісайда

Перетворенням Лапласа називають співвідношення

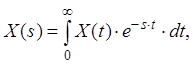
яке ставить функції X(t) дійсної змінної у відповідність функцію X(s) комплексної змінної , де 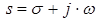. При цьому X(t) називають оригіналом, а X(s) – зображенням або зображенням по Лапласу.

Те, що X(t) має своїм зображенням X(s), або оригіналом X(s) є X(t), записується так:

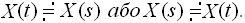
Іноді також користуються символічним записом:

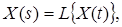
де L – оператор Лапласа.

Передбачається, що функція X(t), яка підлягає перетворенню Лапласа, має такі властивості:

X(t) визначена і кусково-диференційована на всій додатній числовій піввісі [0,∞];
X(t) = 0 при t<0 ;
існують такі додатні числа M і c, що 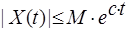при 0 ≤ t< ∞ (росте не швидше, ніж експонента).

Функції, які мають три вказані властивості, називаються функціями-оригіналами.

Співвідношення

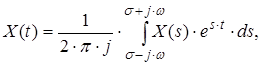
яке визначає за відомим зображенням його оригінал (в точках неперервності останнього), називають оберненим перетворенням Лапласа.

Символічно обернене перетворення Лапласа можна записати так:

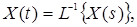
де символ L^-1 – обернений оператор Лапласа.

Для стаціонарних систем (a_i=const) перетворення Лапласа і Хевісайда співпадають.

2.1.2 Інтерпретації перетворення Лапласа

На основі перетворення Лапласа побудований ефективний та ефектний математичний апарат для розв’язку важливих прикладних та теоретичних задач.

Розглянемо одну з найбільш наочних інтерпретацій перетворення Лапласа.

Задача:

Що краще: 5 грн. сьогодні, чи 10 грн. через 5 років?

Як порівнювати економічні результати, отримані в різні моменти часу?

Або більш загальна постановка:

Як привести до одного часового горизонту різні варіанти потоків прибутків і витрат ?

Чи знаєте Ви:

Чому дорівнюють нормовані коефіцієнти окупності капіталовкладень ?

Чому дорівнює позиковий відсоток в банку ?

Віддамо гроші в банк і подивимось, що відбудеться.

Задамо ℷ (норма відсотку)=20% і визначимо через 5 років яким стане вклад 5 грн. в банку.

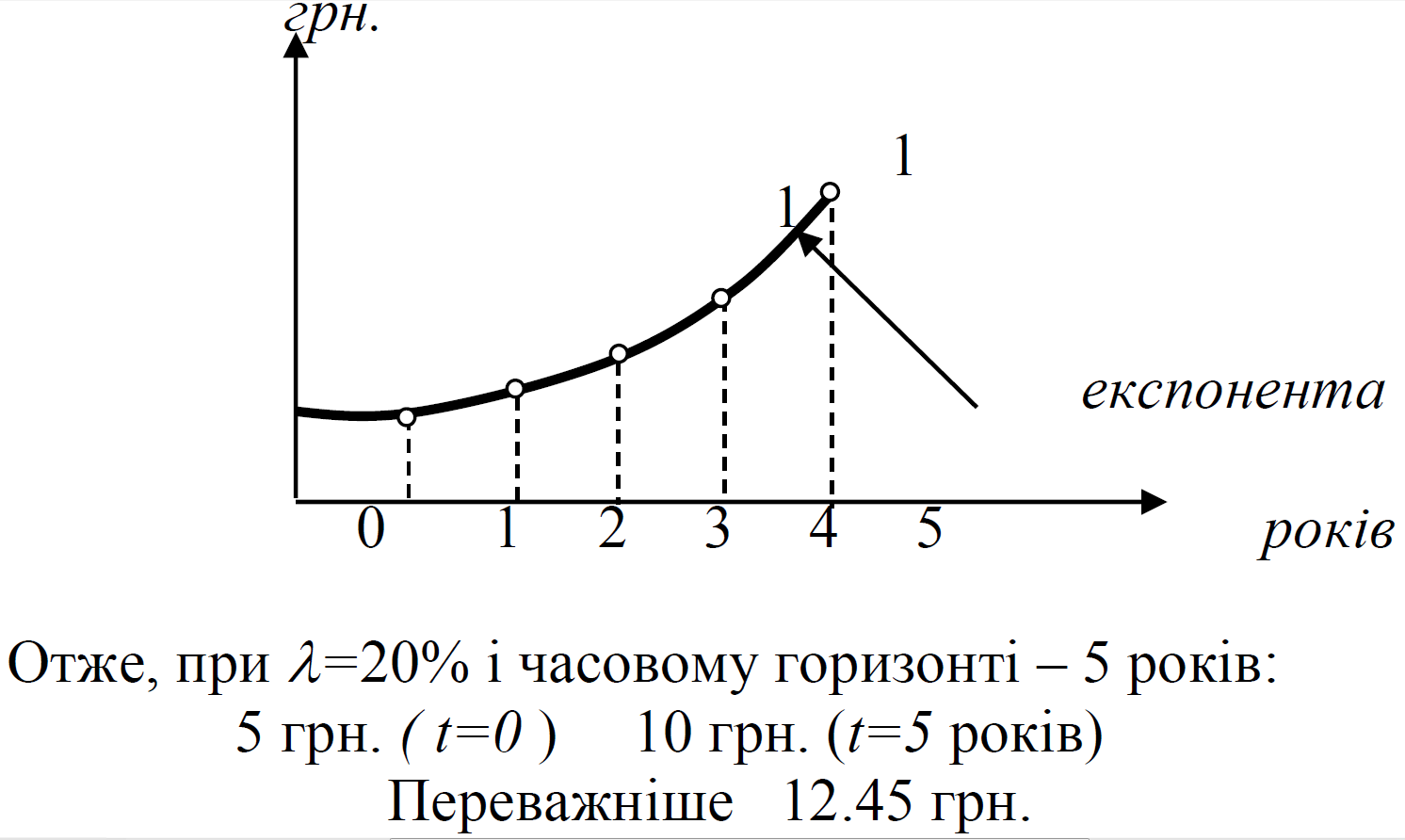
Узагальнимо цю задачу: порівняємо два проекти А і В, які потрібні на початку затрат, а потім дають віддачу.

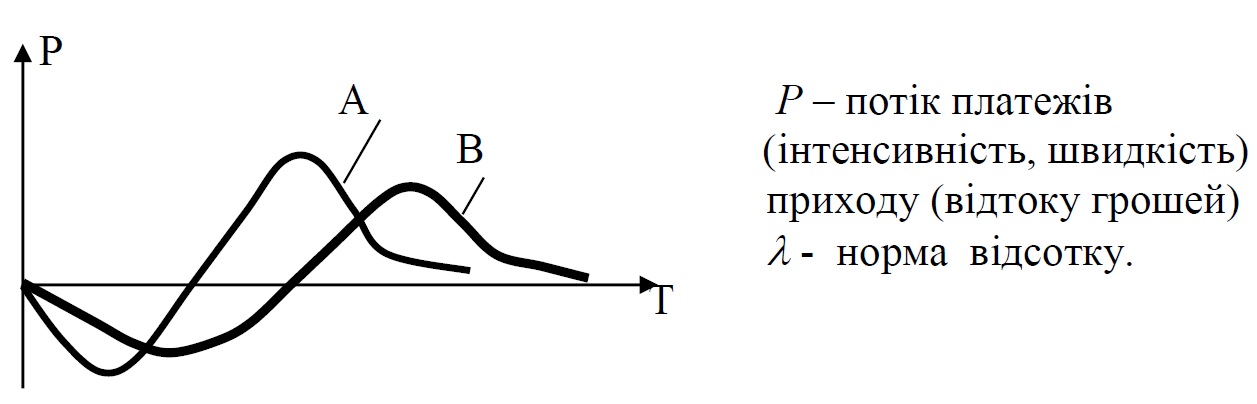
Кожну точку помножимо на експоненту і ці ординати додамо.

Приведені до деякого моменту часу Т сумарні витрати-прибутки будуть виражатися формулою:

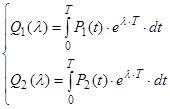
приведений (дисконтований) сумарний прибуток.

Вибір слід зробити після порівняння:

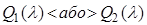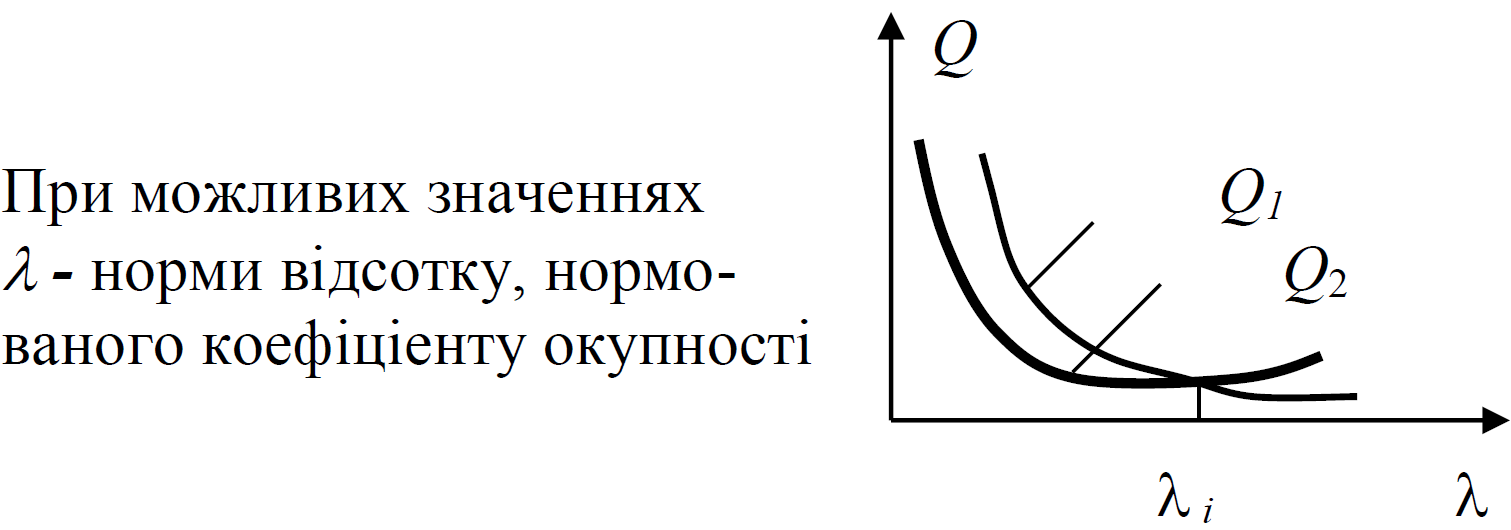
Вищеописана операція давно відома в бухгалтерсько-банківській справі та іменується дисконтуванням.

Але порівняємо формули перетворення Лапласа і дисконтування – вони структурно еквівалентні:

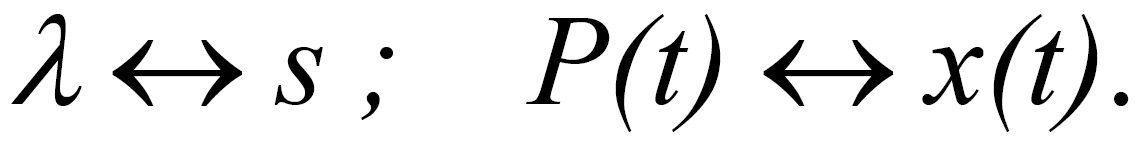
В економіці розглядається кінцевий період часу (інтегрування) (див. A. Холл. Досвід методології для системотехніки).

2.1.3 Властивості перетворення Лапласа

1) Властивість лінійності:

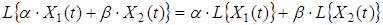2) Диференціювання оригіналу:

Якщо похідна є функцією-оригіналом, то

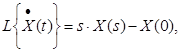
де , далі розглядаємо при нульових початкових умовах.

Якщо n-на похідна 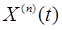є функцією-оригіналом і початкові умови нульові:

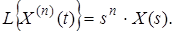
Таким чином, при нульових початкових умовах диференціювання оригіналу відповідає множення зображення на s.

3) Інтегрування оригіналу:

Інтегрування оригіналу зводиться до ділення зображення на s

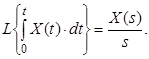
4) Теорема запізнення:

Для будь-якого додатного числа t

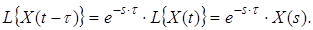
5) Теорема про згортку (теорема множення зображень):

Якщо X₁(t) і X₂(t) – оригінали, а X₁(s) і X₂(s) – їх зображення, то

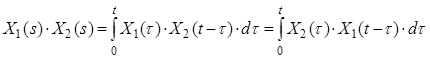Інтеграл правої частини рівності називають згорткою функції X₁(t) і X₂(t) і позначають X₁(t)*X₂(t):

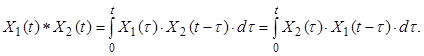
6) Теорема про граничні значення (самостійно!):

Якщо X(t) – оригінал, а X(s) – його зображення, то 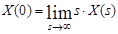і при існуванні границі 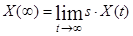, то .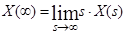

7) Теорема розкладання (самостійно!):

Якщо функція 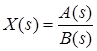, то приводиться залежність X(t) від X(s).

2.1.4 Застосування перетворення Лапласа для розв’язання диференціальних рівнянь. Передаточні функції

Канонічна форма запису диференційних рівнянь для одномірної системи n-го порядку:

(2.1)

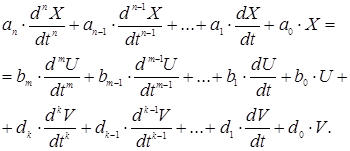
Використовуючи оператор Хевісайда:

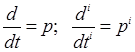рівняння (2.1) перепишемо наступним чином:

(2.2)

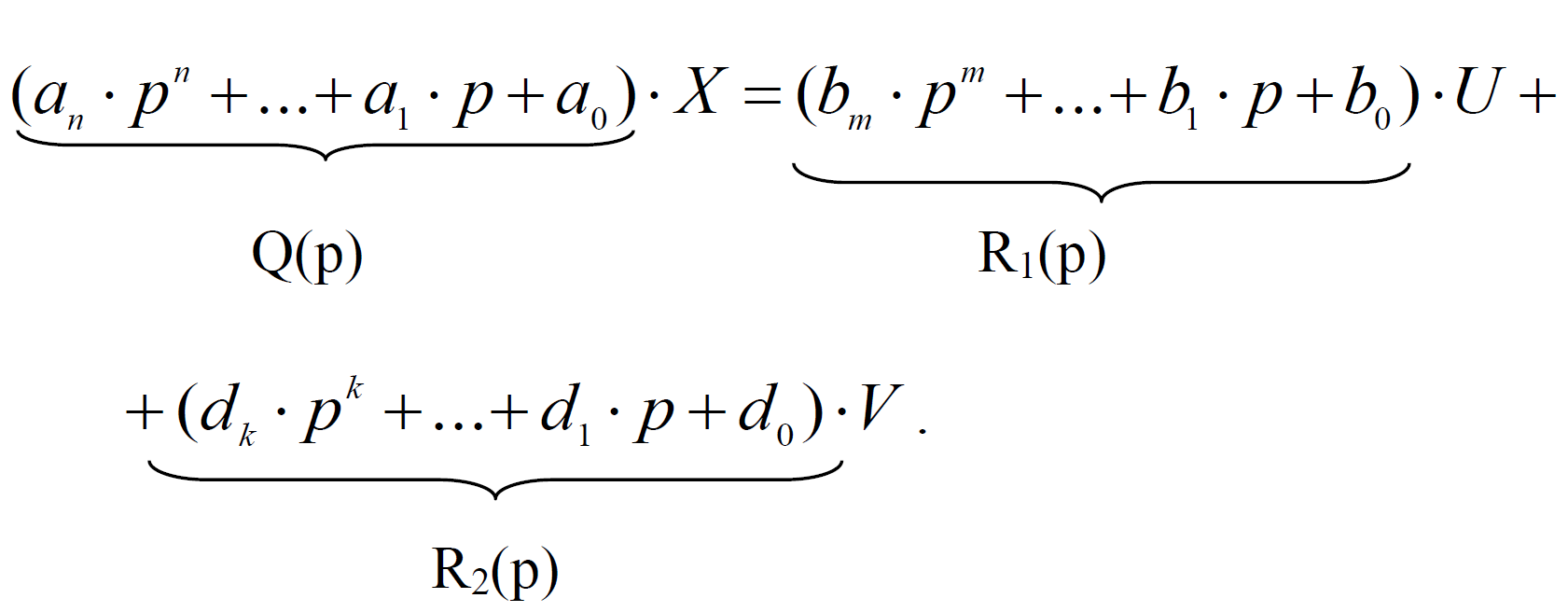
Тоді рівняння (2.1) набуде такого виду:

(2.3)

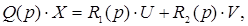
де Q(p) – диференційний оператор при вихідній величині називають власним оператором;

R₁(p) і R₂(p) – диференційні оператори при вхідних величинах – оператори впливу.

Відношення оператора впливу до власного оператора називають передаточною функцією або передаточною функцією в операторній формі.

Передаточна функція W₁ по вхідній величині U:

(2.4)

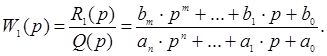
Передаточна функція W₂(р) по вхідній величині V :

(2.5)

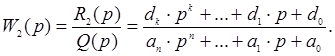
Використовуючи передаточні функції, рівняння (2.1) запишемо у вигляді:

(2.6)

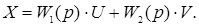
Рівняння (2.3) і (2.6) називають рівняннями в символічній або операторній формі запису.

Одночасно з передаточною функцією в операторній формі широко використовують передаточну функцію в формі зображень Лапласа.

Передаточною функцією або передаточною функцією в формі зображень Лапласа називають відношення зображення вихідної величини до зображення вхідної величини при нульових початкових умовах.

Якщо система має декілька входів, то при визначенні передаточної функції відносно якої-небудь вхідної величини інші величини вважають рівними нулю.

(2.7)

(2.8)

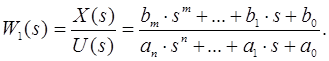
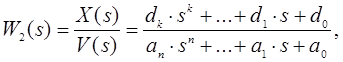
Передаточну функцію в формі зображень Лапласа можна отримати з передаточної функції в операторній формі, якщо в останній зробити підстановку р=s.

В загальному випадку це виходить з того, що диференціюванню оригінала (символічне множення оригінала на р) при нульових початкових умовах відповідає множенню зображення на комплексне число s.

Схожість між передаточною функцією в формі зображень Лапласа і в операторній формі чисто зовнішня. Вона має місце тільки у випадку стаціонарних систем.

Використовуючи передаточні функції (2.7), (2.8) в зображеннях Лапласа можна записати:

(2.9)

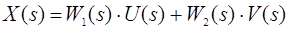
Рівняння (2.9), як і рівняння (2.6), адекватне рівнянню (2.1) тільки при нульових початкових умовах.

2.1.5 Передаточні функції багатомірних САУ

Дано: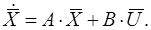

Необхідно отримати: - передаточну функцію одномірної САУ;

- передаточну матрицю багатомірної САУ.

Розв’язання:

Виконаємо перетворення Лапласа:

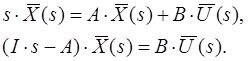
Вирішимо формально:

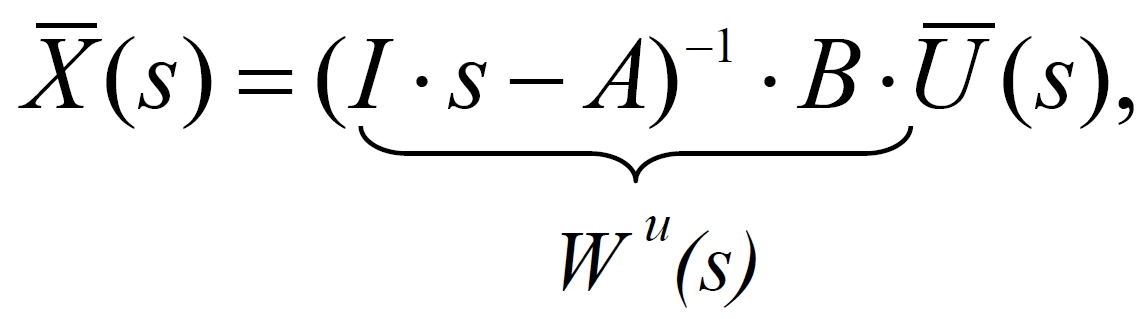
де W^u(s)– передаточна матриця.

У скалярному вигляді:

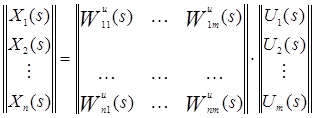де W_ij^u(s) – елементи матриці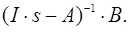

Як відомо з курсу вищої математики, обернена матриця деякої матриці M(s)

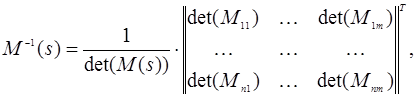
де Т – знак транспонування;

M_{i j} – алгебраїчне доповнення до елемента m_{i j} .

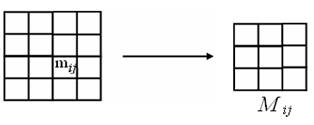
Елементи передаточної матриці W^u(s) – дробово-раціональні функції від s, вони називаються передаточними функціями для i-ої змінної вектора стану по j-му управляючому впливу, тобто

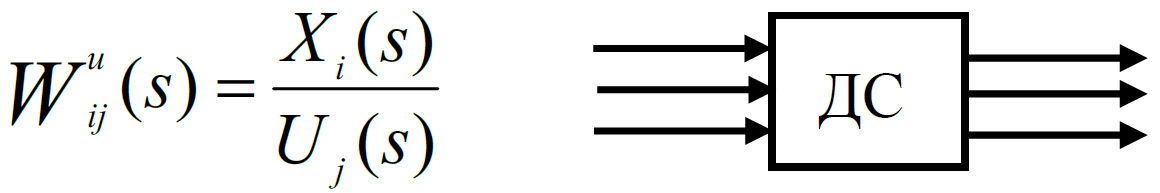
інші впливи, крім U_j, дорівнюють нулю.

Для лінійних систем справедливий принцип суперпозиції.

2.2 Частотні характеристики

2.2.1 Експерементальне та аналітичне отримання ЧХ

ЧХ (частотні характеристики) – залежність амплітуди і фази від частоти.

ЧХ – стандартний інструмент оцінки якості не тільки САУ, але й акустичних, радіотехнічних та інших систем.

Дано:

де ГЧ – генератор частоти.

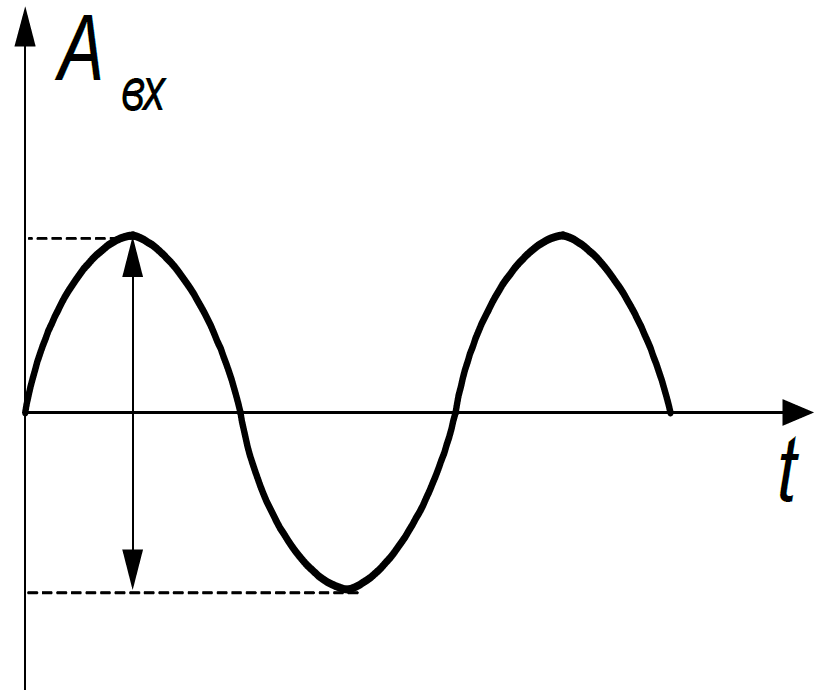
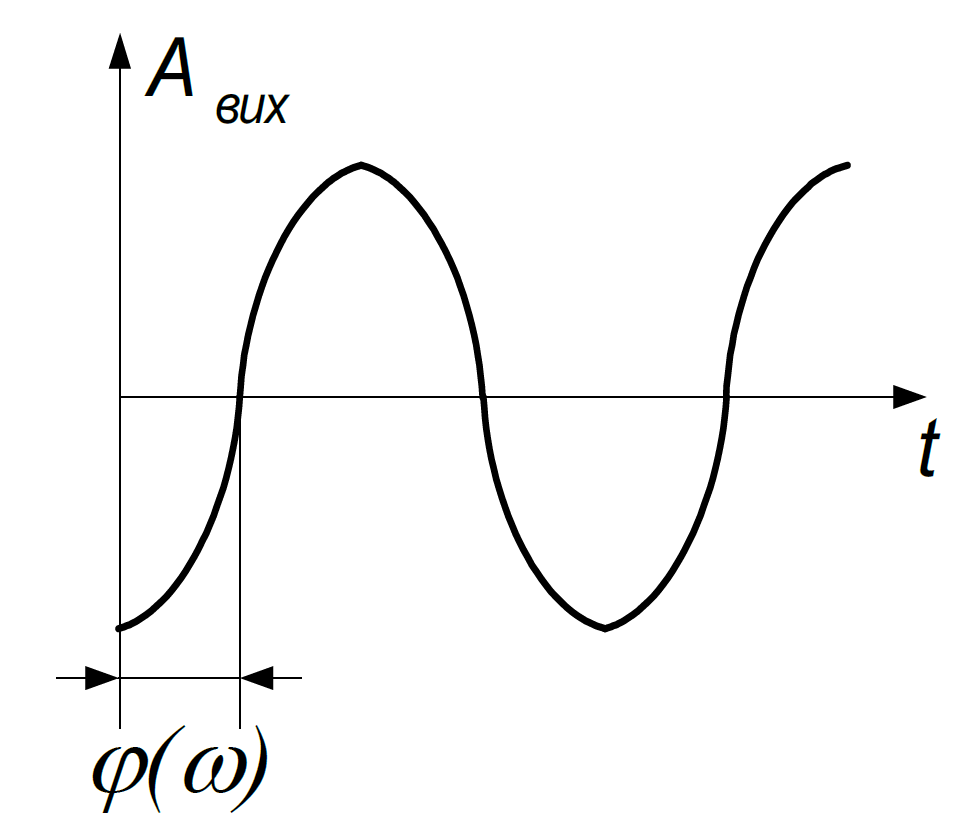
Виміряємо A_вих, φ_вих і побудуємо графіки.

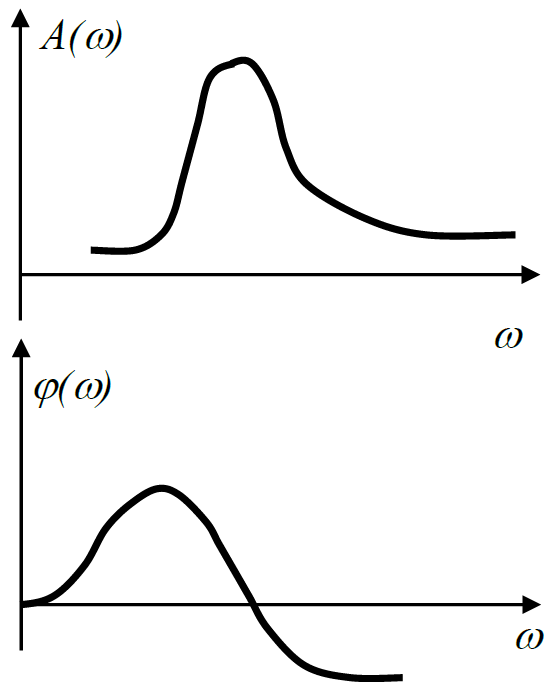
АЧХ – амплітудна характеристика завжди додатня.

ФЧХ – фазова характеристика

2.2.2 Аналітичне отримання ЧХ

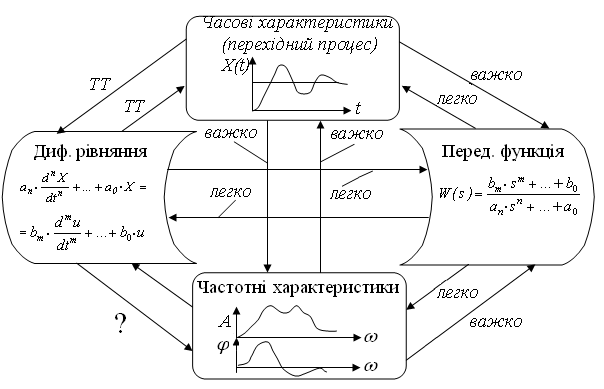
де ТТ – дуже важко визначити.

Всі описи формально рівноцінні – несуть одну і ту ж інформацію. Вибір того або іншого засобу опису лінійної динамічної системи (ЛДС) залежить від умов розв’язку задачі, традицій тощо.

Частотні характеристики можна отримати експериментально і аналітично, якщо є опис у вигляді передаточної функції. Процедура отримання ЧХ по передаточній функції дуже проста.

Дано: Передаточна функція

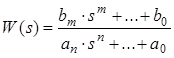Потрібно визначити: А(ω), φ(ω) - ?

Розв’язок:

1) Замість s підставляємо jω:

s → jω.

Отримаємо:

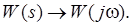
W(jω) – називають частотною передаточною функцією;

ω – називають частотною змінною.

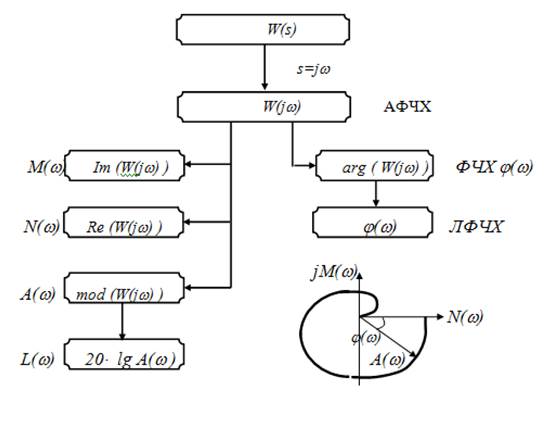
2) 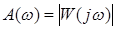називають амплітудно-частотною функцією, її графік – амплітудною частотною характеристикою (АЧХ).

Аргумент 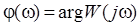називають фазовою частотною функцією, її графік – фазовою частотною характеристикою (ФЧХ).

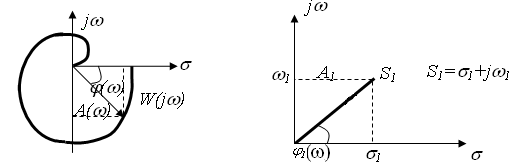
Комплексне число можна записати через амплітуду А₁ і фазу φ₁:

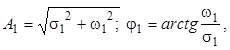
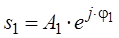– тригонометрична форма.

Як знайти модуль:

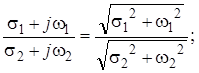
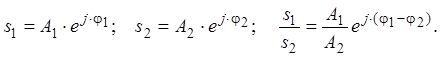
Всі передаточні функції дробово-раціональні вирази.

2.2.3 Приклади отримання ЧХ

Дано:

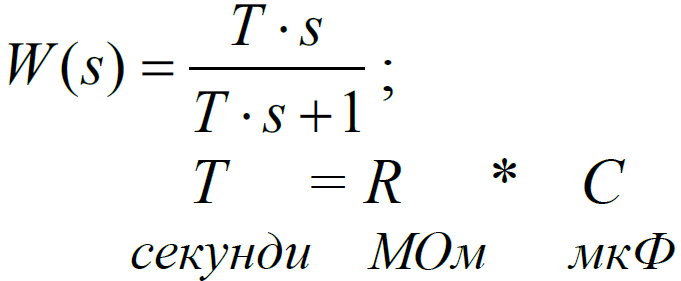
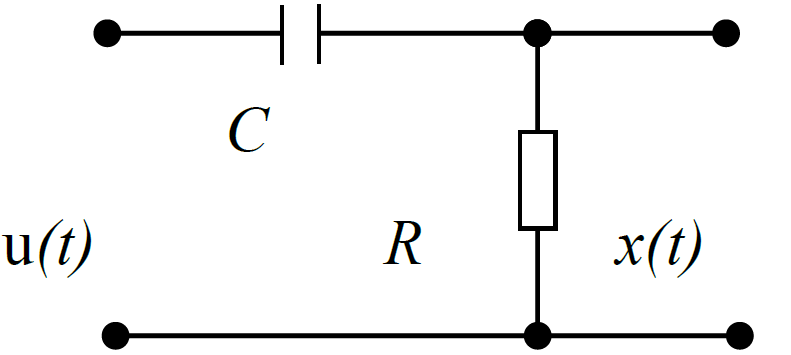
(доведіть, що Т вимірюється в сек.)

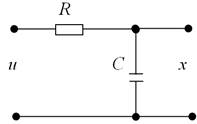
Зовсім різні по фізичному змісту пристрої часто мають однакові передаточні функції. Розглянемо гідравлічну систему :

гідравлічна ємність

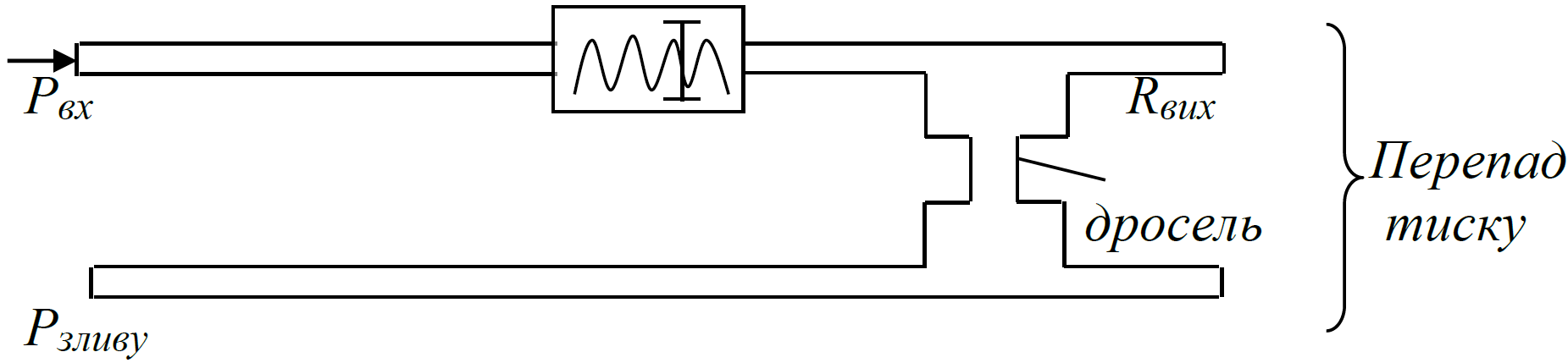
Аналітичне отримання ЧХ :

s → jω.

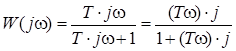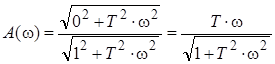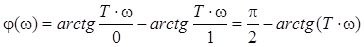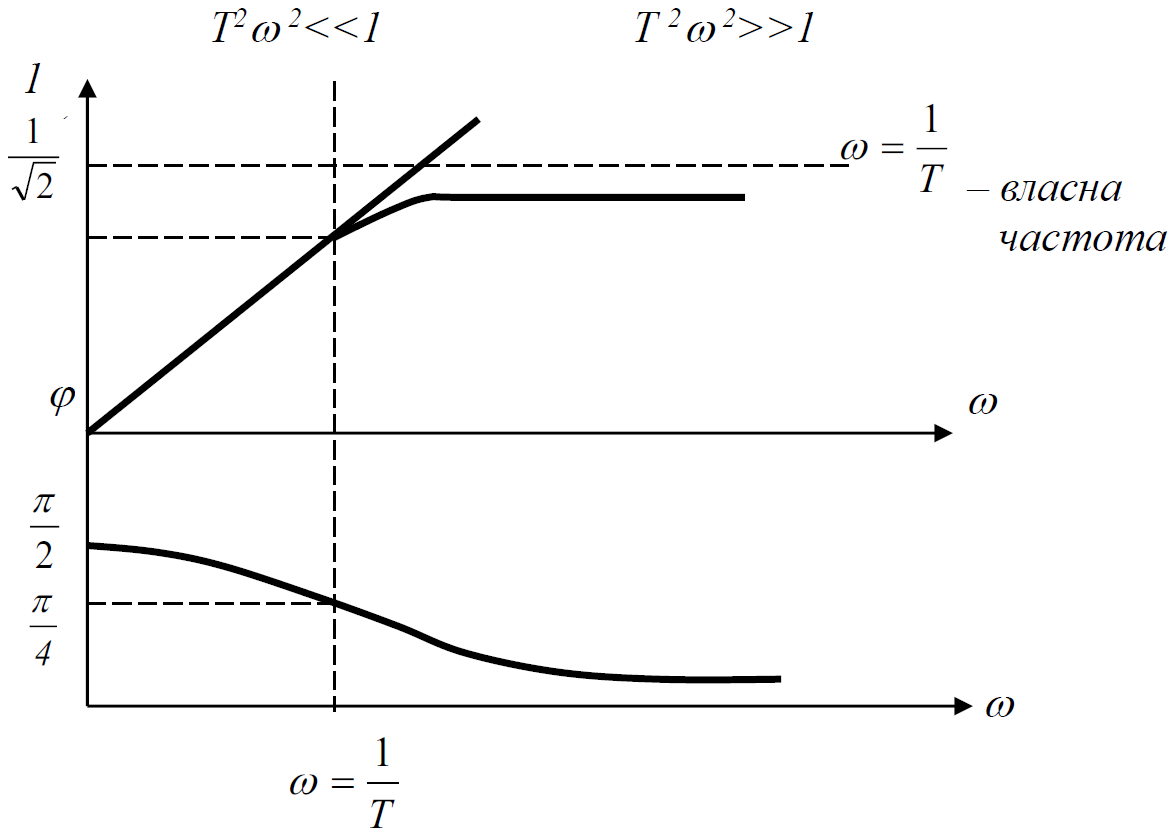
Отримаємо частотні характеристики, якщо

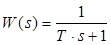
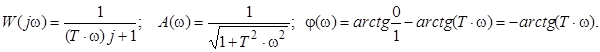
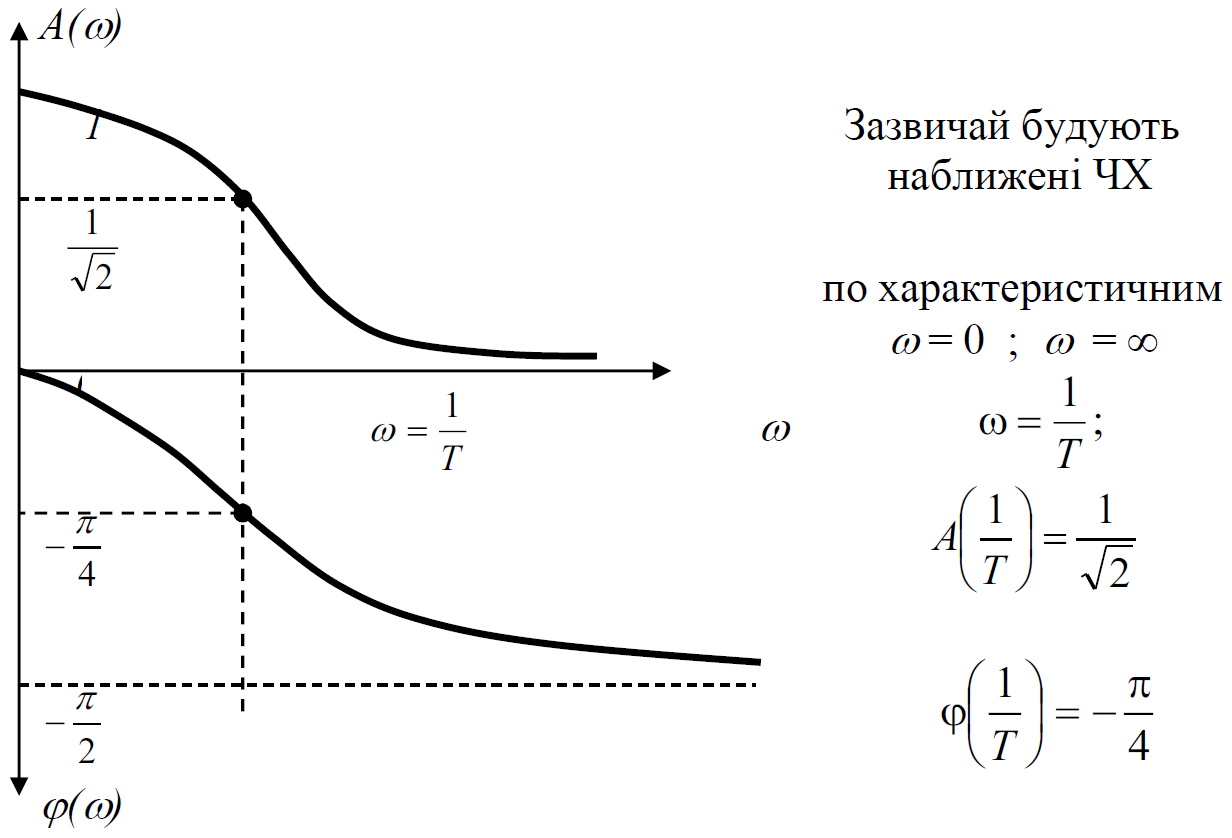
Завдання для самостійної проробки

Знайти передаточні функції і побудувати частотні характеристики слідуючих ланцюгів:

2.2.4 Виведення аналітичного виразу для ЧХ

Отже, ми вже знаємо, що ЧХ можна отримати експериментально і аналітично з передаточної функції підстановкою s = jω. Давайте перевіримо, що ця формальна процедура дозволяє отримати ЧХ.

Дайте словесне визначення експериментальної процедури
отримання для деякого конкретного значення ω одної точки
ЧХ.

Відповідь: подати на вхід ЛДС сигнал постійної амплітуди і частоти U_вх., почекати коли закінчиться перехідний процес і виміряти А(ω), j(ω).

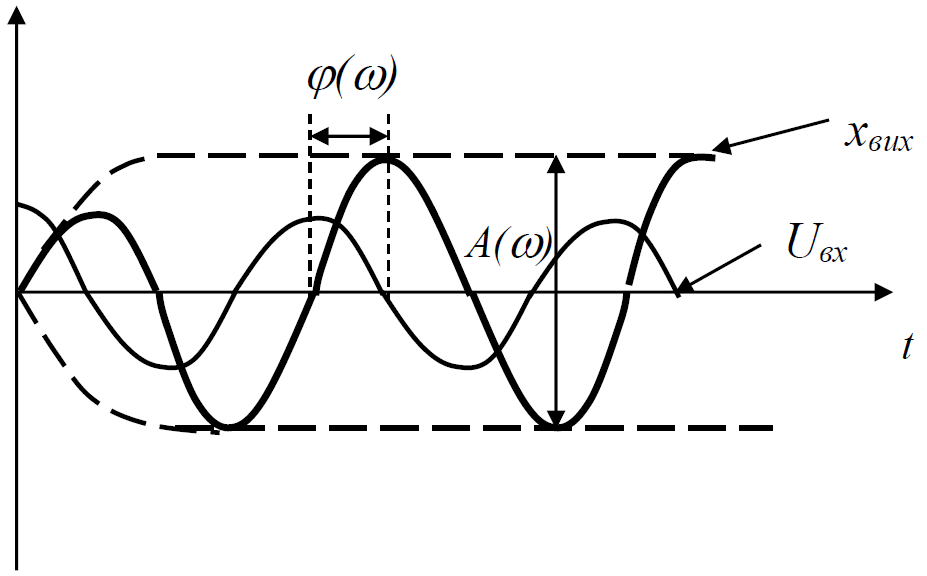
Переформулюємо це визначення на мову диференціальних рівнянь: отримаємо загальне рішення неоднорідного диференціального рівняння, яке описує ЛДС з правою частиною і розглянемо його рішення при t→ ∞.

Дано: ЛДС задана диференціальним рівнянням в канонічному вигляді:

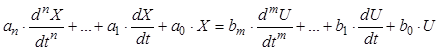
або .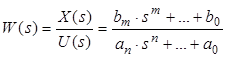

На вхід ЛДС подається гармонійний вплив:

Знайти вигляд рішення X(t) при t→ ∞.

Обмеження: 1) n ≥ m;

2) ЛДС стійка.

Повторення:

З теорії лінійних диференціальних рівнянь відомо, що: 1) рішення однорідного диференціального рівняння:

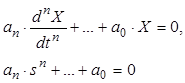має вигляд: 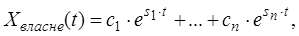де s₁,...,s_n – корені характеристичного рівняння. Якщо корені s₁,...,s_nмають від’ємні дійсні частини, то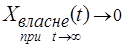

– система стійка. 2) загальний розв’язок неоднорідного диференціального рівняння має вигляд: , для стійкої системи:

З теорії диференціальних рівнянь відомо, що окремі рішення шукаються в тій же формі, що і вхідний сигнал:

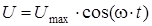Розв’язок:

1) Використаємо для представлення U(t) формулу Ейлера:

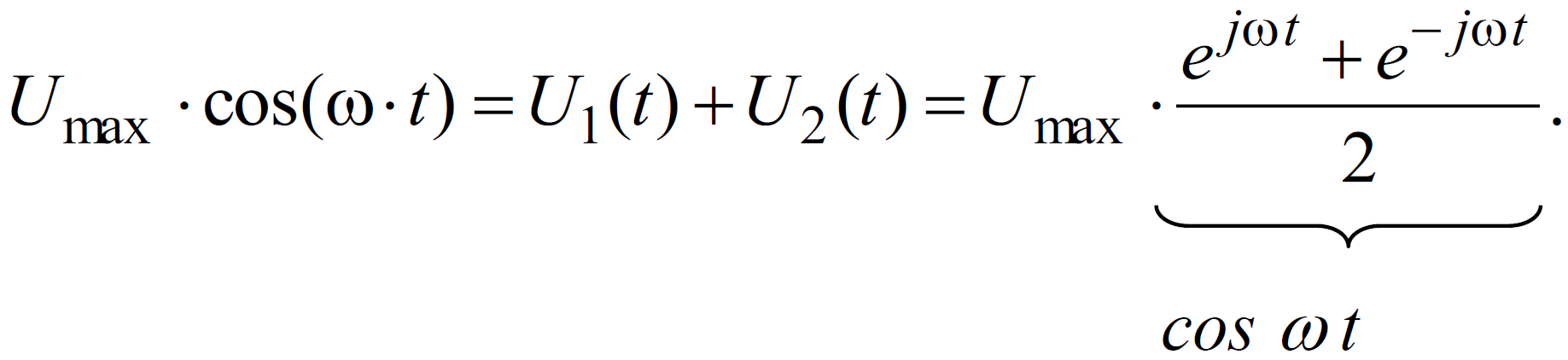
2) Використаємо принцип суперпозиції, справедливий для лінійних систем:

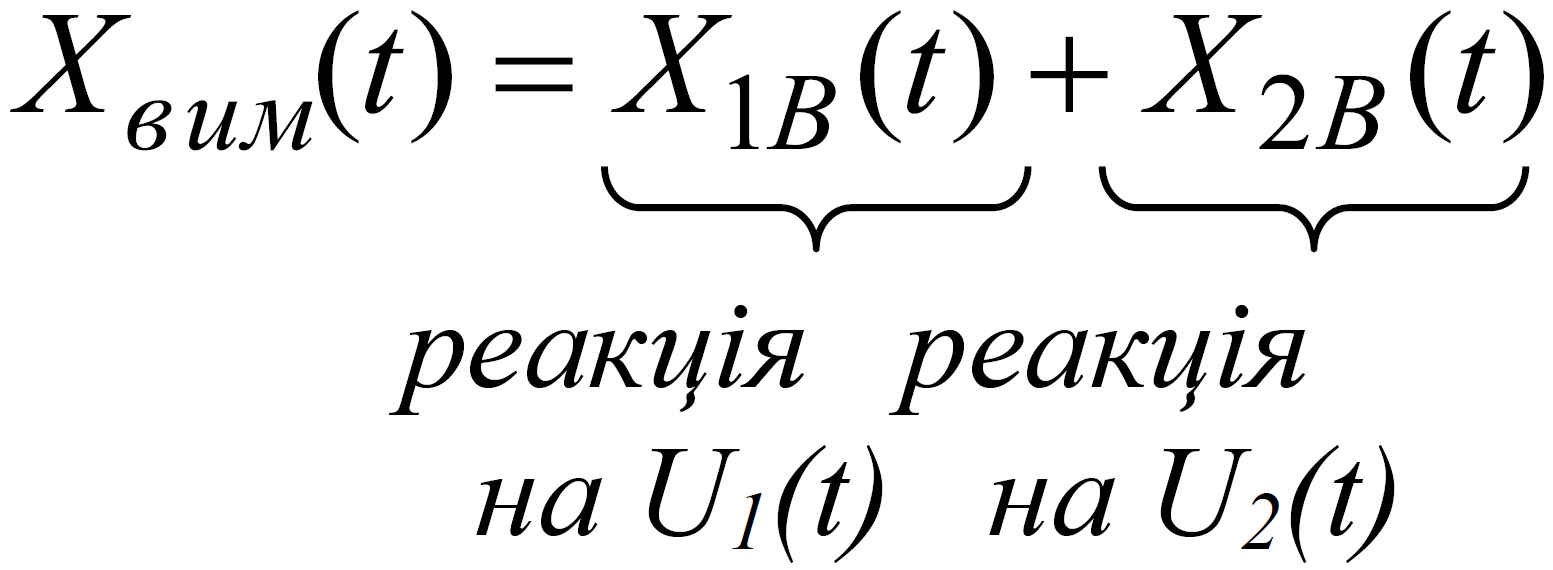
3) Згідно теорії диференціальних рівнянь:

де А₁ , А₂ – коефіцієнти, які підлягають визначенню.

4) Підставимо в перше диференціальне рівняння вираз для

Врахуємо, що …,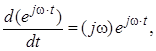

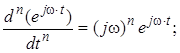
З урахуванням цього:

Звідси: ,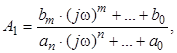

за визначенням: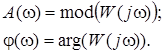

Аналогічно отримаємо рішення для U₂(t):

А тепер запишемо вимушене рівняння:

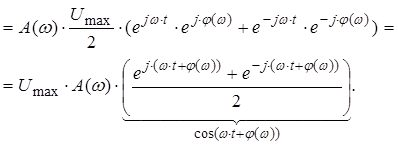
Дійсно, вихід – гармонійне коливання з амплітудою і фазою відносно вхідного сигналу.

2.2.5 Логарифмічні частотні характеристики

При використанні логарифмічних масштабів частотні характеристики набувають простого стандартного виду і набагато зрозумілішого, ніж при використанні натуральних масштабів.

Прологарифмуємо W(jω):

–

Однак, прийнято брати lg і множити на 20 (за традицією з акустики), тому

L(ω) = 20• lg A(ω) – ЛАЧХ (логарифмічна АЧХ);

φ(ω) – ЛФЧХ (логарифмічна ФЧХ).

Для ЛАЧХ і ЛФЧХ використовуються наступні шкали і одиниці вимірювання:

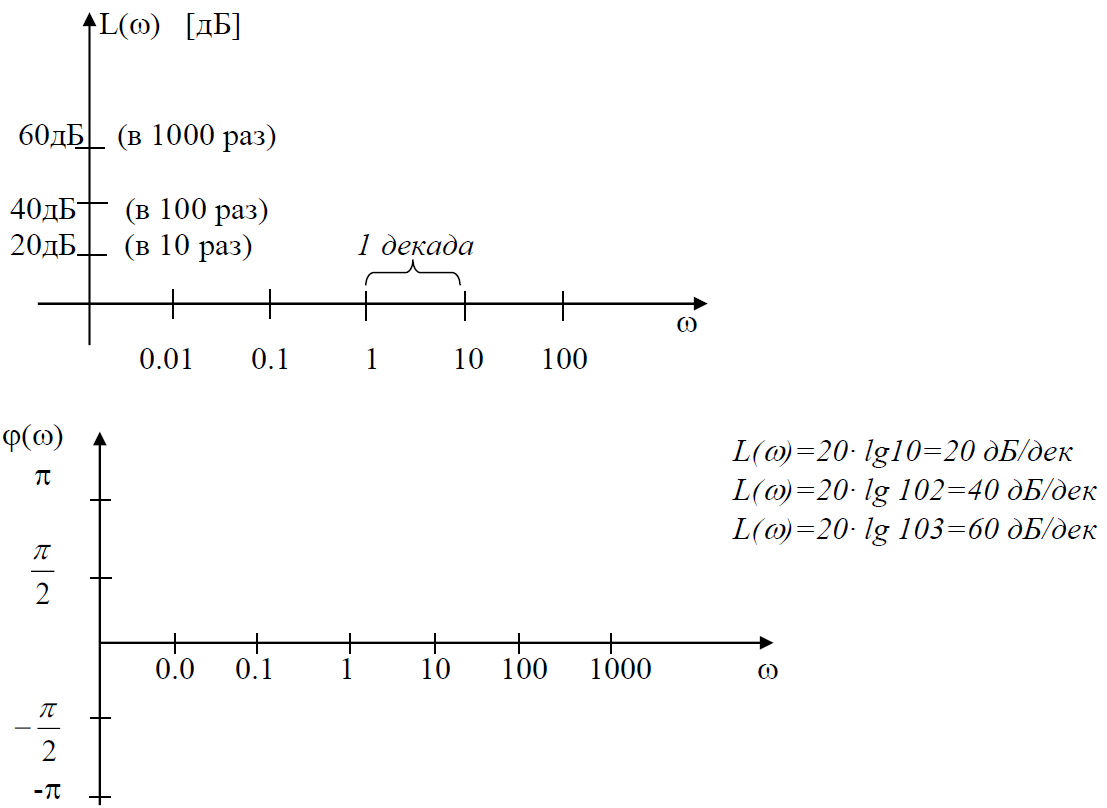
При побудові ЛФЧХ величина φ відкладається в натуральному (нелогарифмічному) масштабі.

Історично склалося так, що одиницею для L(ω) вибрано 1 дБ, вимірювання частоти задається в октавах або декадах, зміна ω в 4, 10 раз відповідно.

Декадою називають інтервал, на якому частота змінюється в 10 раз.

Вісь ординат при будуванні ЛАЧХ проводять крізь довільну точку, не через точку ω=0 , звичайно за початок відліку беруть ω_min.

Нахил L(ω) вимірюється в децибелах на декаду. Наприклад, нахил 20 дБ/дек означає, що при зміні частоти в 10 раз, амплітуда змінюється в 10 разів.

Логарифмічні графіки можуть бути наближені прямими.

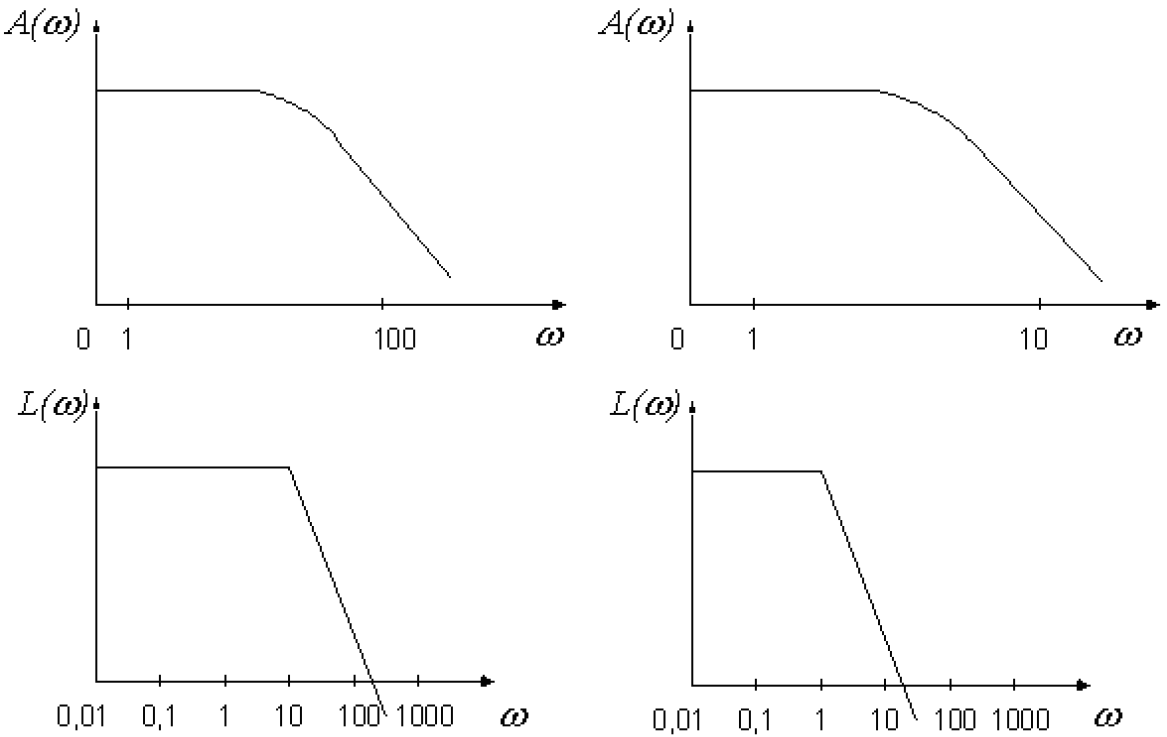
Питання:

2.2.6 Приклад отримання ЛАЧХ

(аперіодична ланка);

;

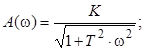
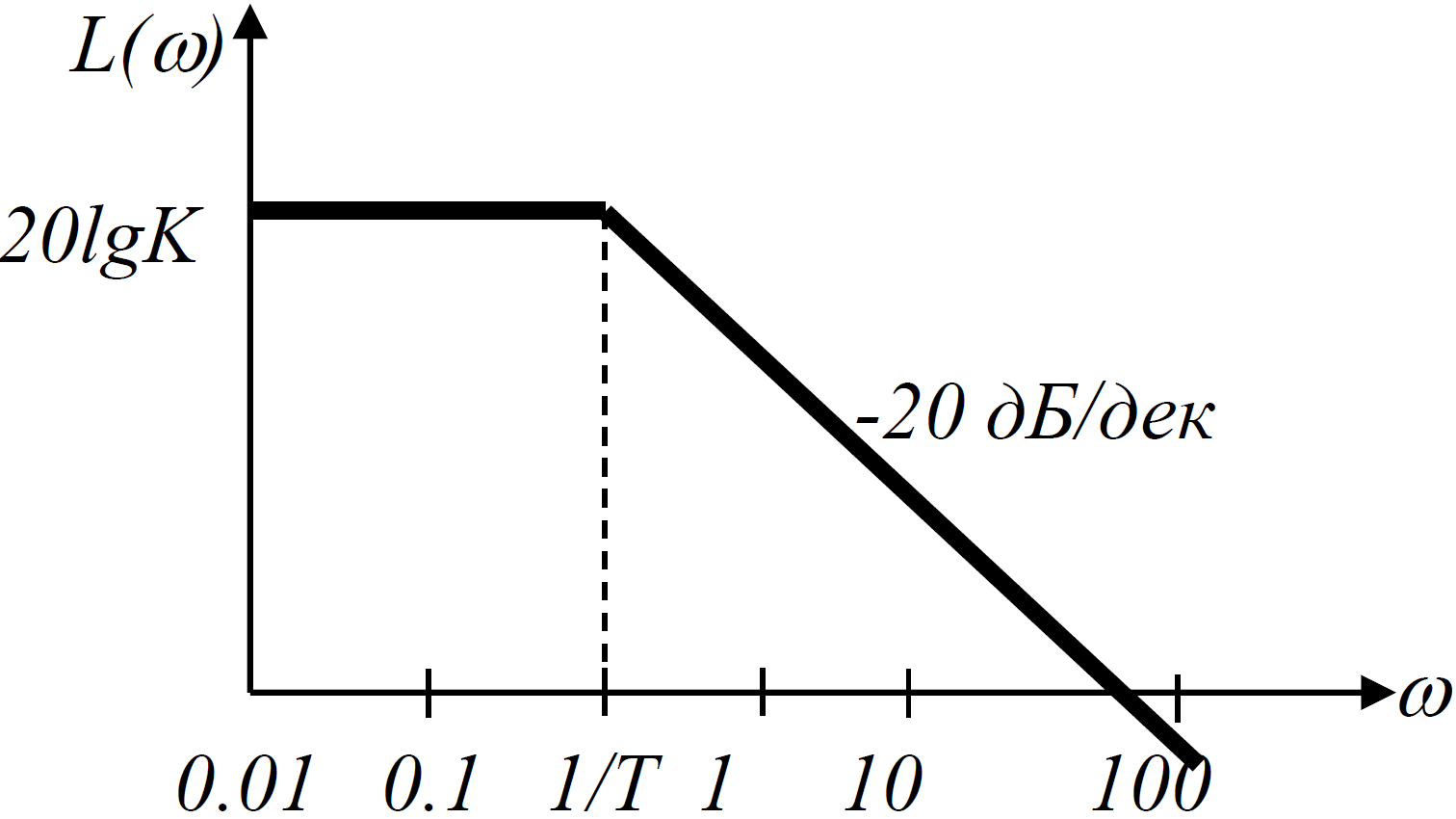
Дослідження L(w) при малих і великих частотах, ;

2)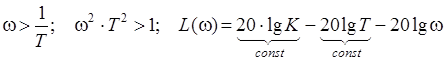 - рівняння прямої з нахилом -20 дБ/дек.

2.2.7 Класифікація частотних характеристик

2.3 Часові характеристики

2.3.1 Вагова та перехідна функції

Важливими характеристиками САУ є перехідні функції – часові характеристики.

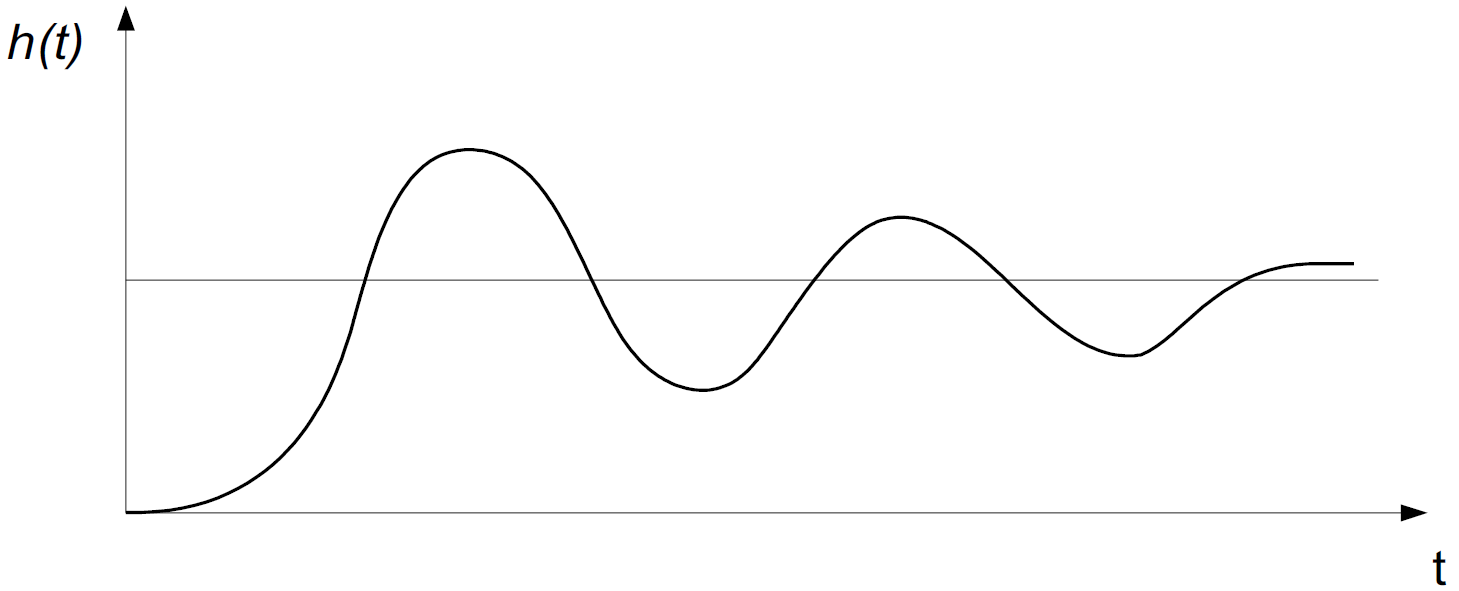
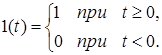
Перехідна функція h(t) є функцією, яка описує реакцію системи на одиничний 1(t) вплив при нульових початкових умовах.

Аналітично одиничний ступінчастий вплив описується одиничною функцією:

Перехідною або ваговою функцією w(t) (функцією ваги) системи називають функцію, яка описує реакцію системи на одиничний імпульсний вплив при нульових початкових умовах.

Фізично одиничний імпульс можна уявити як дуже вузький імпульс, який обмежує одиничну площину :

Математично він описується дельта-функцією δ(t) (узагальненою функцією).

Похідна від 1(t) рівна δ(t):

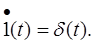
(з теорії узагальнених функцій)

Знайдемо зображення за Лапласом від d(t) та її похідних:

(2.10)

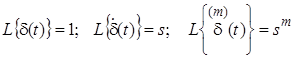Диференціальне рівняння в зображеннях за Лапласом має вигляд:

(2.11)

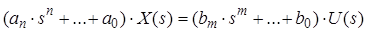або

(2.12)

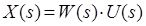Легко перевірити, використовуючи формули (2.10), що рівняння (2.12) справедливе і в тих випадках, коли U=1(t) або U=δ(t).

У відповідності з визначенням вагової функції при U=δ(t) змінна X(t)=w(t).

І так як 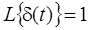, то рівняння (3) можна записати:

(2.13)

(2.14)

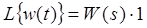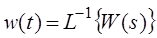Встановимо зв’язок між w(t) і h(t). Так як 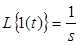, то рівняння (2.12) при u=1(t) набуде вигляду:

(2.15)

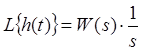Порівнявши рівняння (3.6) і (3.4), не важко помітити, що

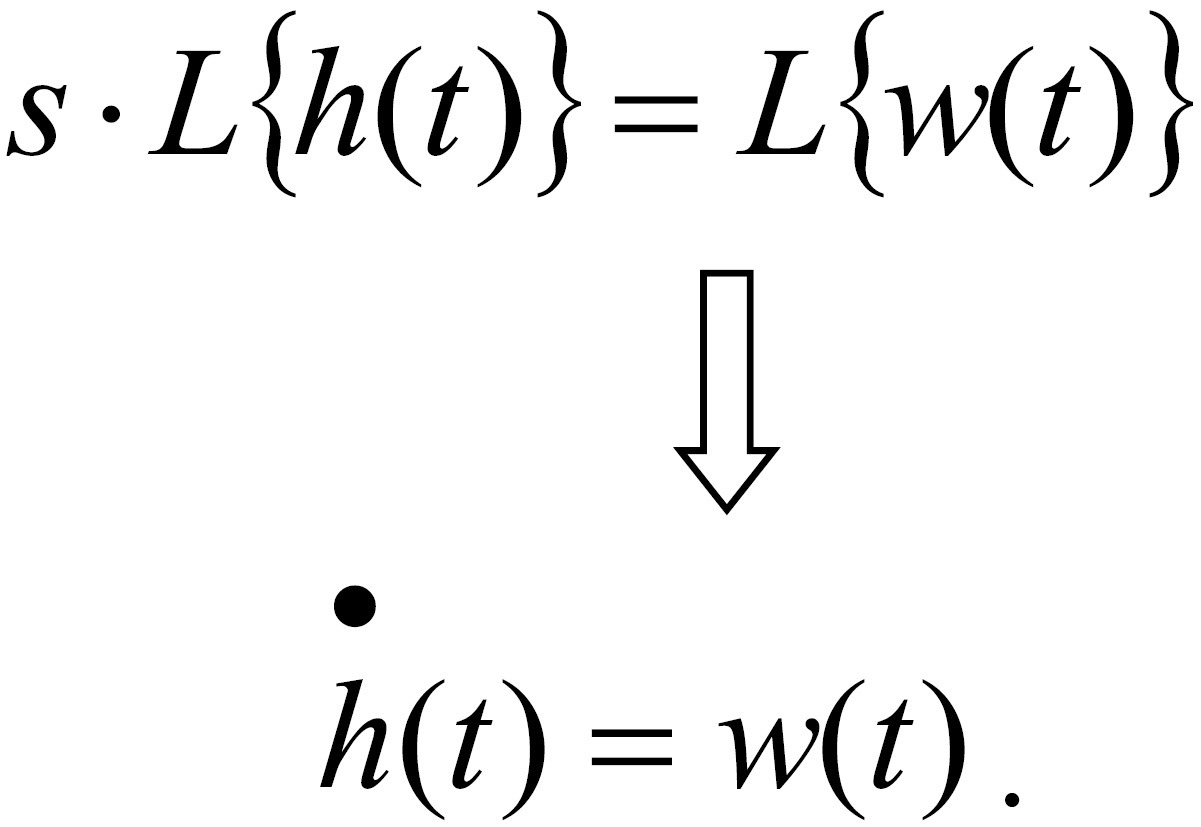
Вагова і перехідна функції, як і передаточна функція, є вичерпними характеристиками системи (ланки) при нульових початкових умовах. За ними можна однозначно визначити вихідну величину при довільному вхідному впливу. Дійсно, виходячи з рівняння (2.12), за допомогою теореми про згортку можемо записати:

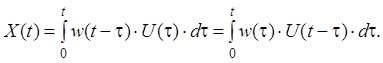
Ця формула вірна тільки при нульових початкових умовах.

2.3.2 Часові характеристики багатомірних САУ. Перехідна функція стану

Ми отримаємо часові залежності вхід-вихід для ЛДС з одним входом і одним виходом:

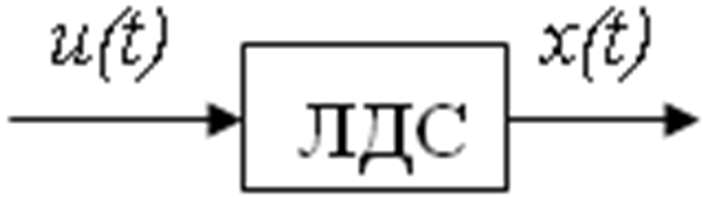
Рисунок 3.1 – Часові залежності «вхід-вихід» для ЛДС

Для ЛДС, які представлені в формі Коші – як одномірних, так і звичайно багатомірних – використовується трохи інший підхід до отримання часових характеристик.

Повторення:
Нехай дана одномірна система першого порядку:

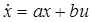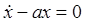
Приймаємо u=0 (замкнута система). Відомо, що рішення рівняння:

має вигляд:

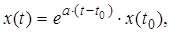
де, x(t₀) – початкова умова,

тобто :

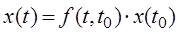Згадаємо розклад в ряд для експоненти:

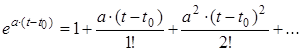
Можете перевірити (самостійно по підручнику!), що для багатомірних САУ має місце аналогічний результат:

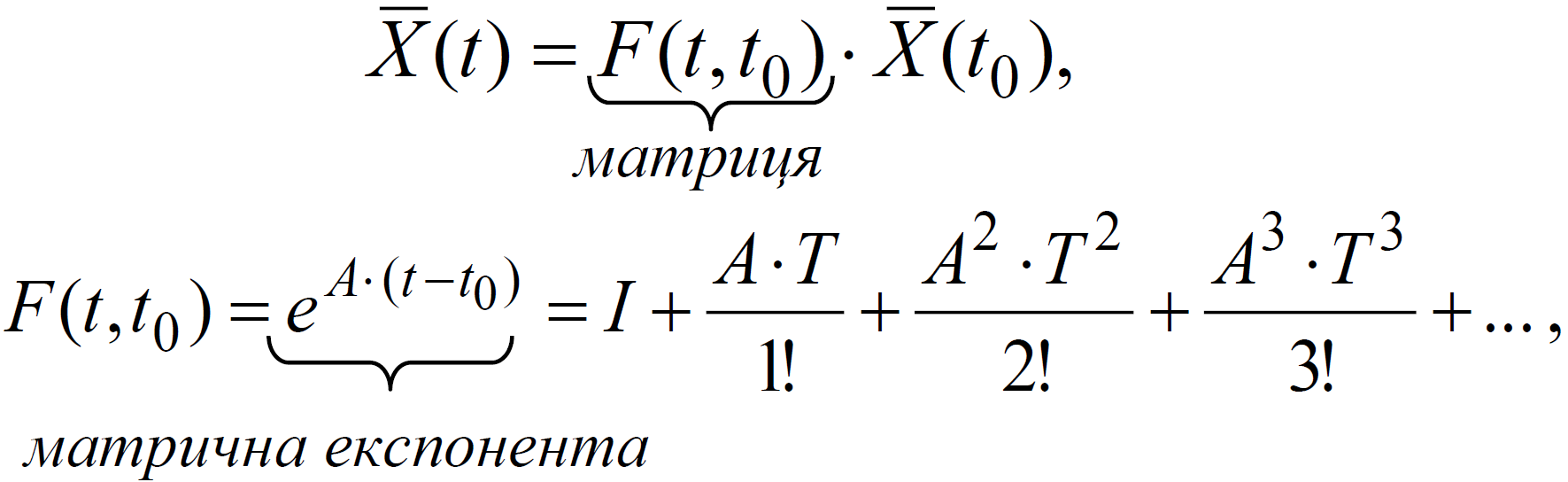
де t-t₀=T; F(t,t₀) або F(Т) – перехідна функція стану.

F(Т) – міст до імпульсних і цифрових САУ. У другій частині курсу ми розглянемо часові характеристики САУ більш детально, а зараз доцільно відмітити, що в типовому представленні імпульсна САУ:

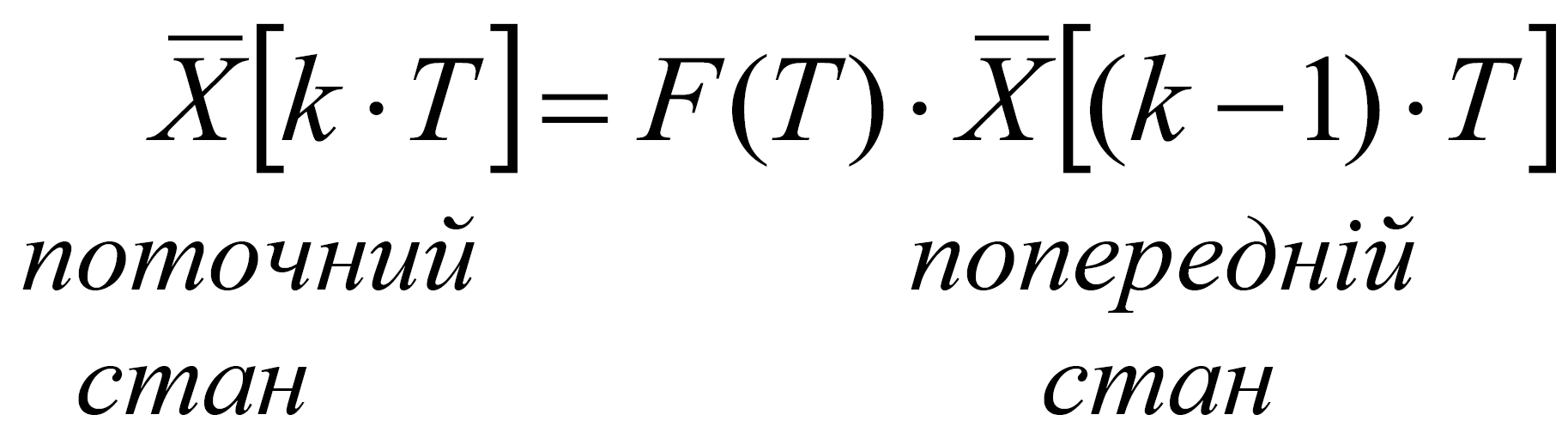
В якості F(Т) використовуємо більше або менше число складових розкладів.

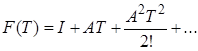
2.4 Математичні моделі елементарних ланок САУ

2.4.1 Елементарні ланки та їх характеристики

Вcе різноманіття лінійних систем можна звести до системи більш простих елементів.

Кожна ЛДС може бути представлена у вигляді з’єднання кінцевого типу елементарних ланок.

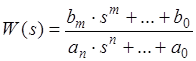де знаменник та чисельник − поліноми.

Основна теорема алгебри: алгебраїчне рівняння n-ого степеня має n-коренів.

За теоремою Безу припустимо, що знайшли всі корені рівняння від s_n до s₀, тоді розкладемо поліном на співмножники:

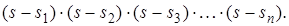
Всі коефіцієнти 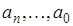– дійсні числа, так як вони звичайно являють собою R, C, момент інерції, коефіцієнт пропорційності, тобто завжди представляють дійсні величини.

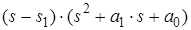– поліном з дійсними коефіцієнтами можна розкласти на поліноми з дійсними коефіцієнтами із степенем не вище другого.

Елементарна (типова) ланка – це ланка, передаточна функція якої має певні особливості

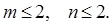
Поліном з комплексними коефіцієнтами зустрічається при обробці голограм, зображень, сейсмограм, в методах просторових фільтрацій.

Таблиця 1 – Класифікація елементарних ланок
№	Ланка	W(S)
1	Пропорційна (підсилювальна)
2	Диференціююча
3	Інтегруюча
4	Форсуюча
5	Аперіодична
6	Коливальна 0 < x < 1
7	Консервативна x = 0
8	Аперіодична 2-го порядку x ³ 1	(2 аперіодичних ланки 1-го порядку)
9	Форсуюча 2-го порядку
10	Чистого запізнення

1) Пропорційна ланка (підсилювальна).

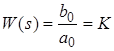
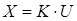
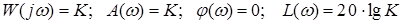
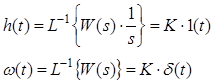
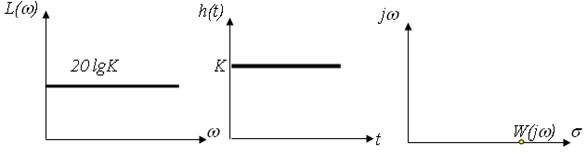
2) Диференціююча ланка.

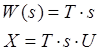
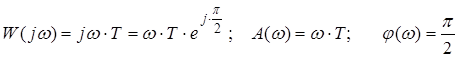
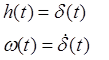
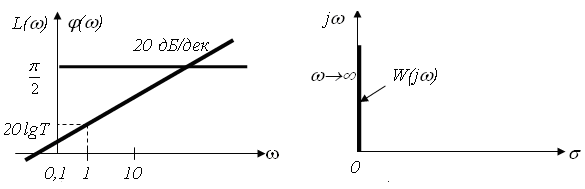
3) Інтегруюча ланка.

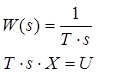
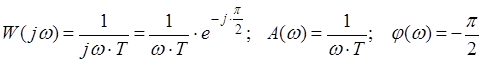
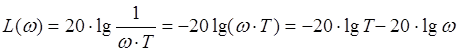
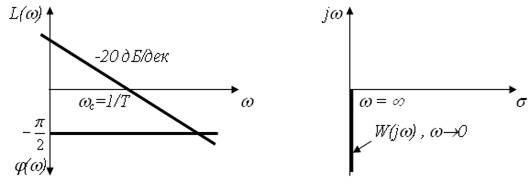
4) Форсуюча ланка.

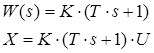
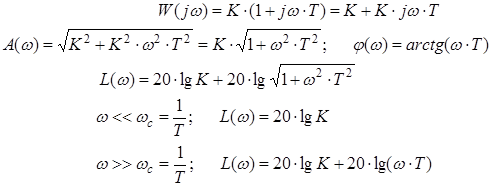
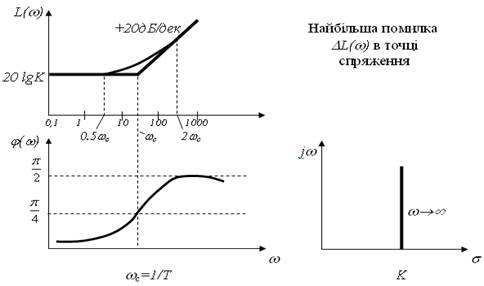
5) Аперіодична ланка.

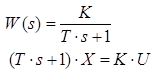
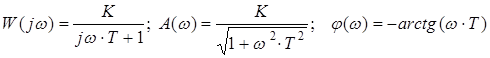
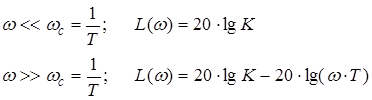
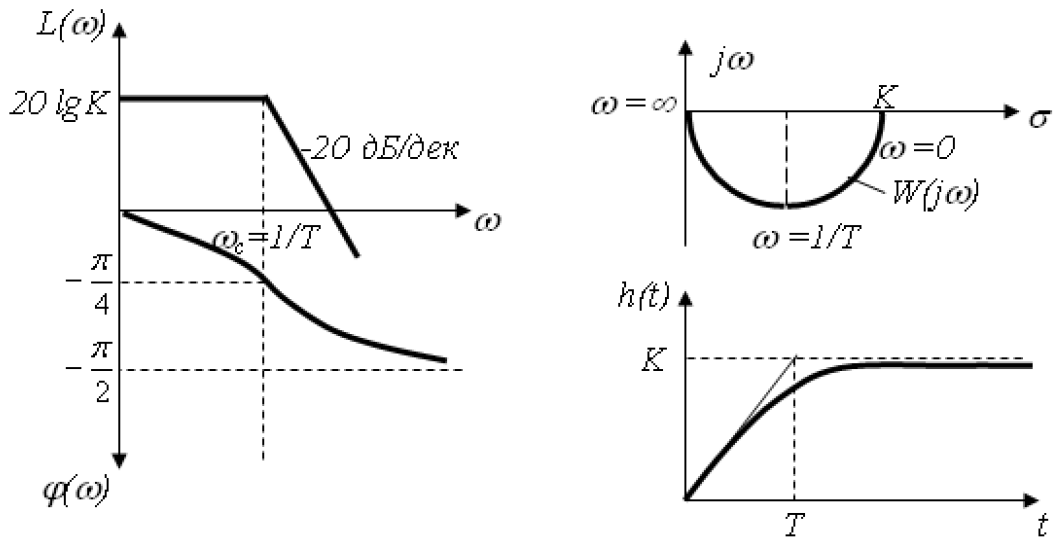
6) Коливальна ланка (0 < x < 1), x − коефіцієнт демпфування.

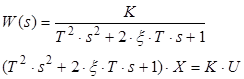
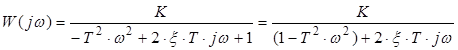
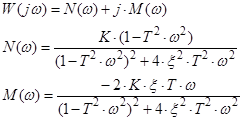
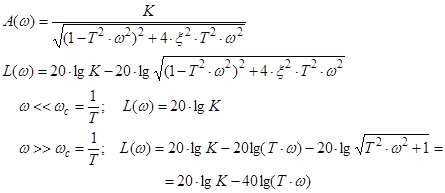
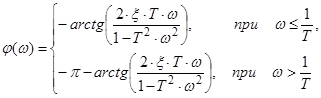
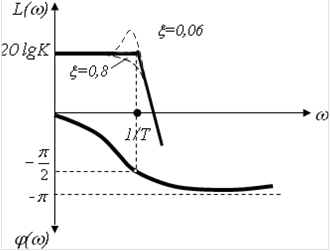
Слід мати на увазі, що асимптотична ЛАЧХ при малих значеннях коефіцієнта демпфування дуже сильно відрізняється від точної ЛАЧХ.

Розглянемо як впливає варіація параметрів ξ і Т на частотні характеристики коливальної ланки.

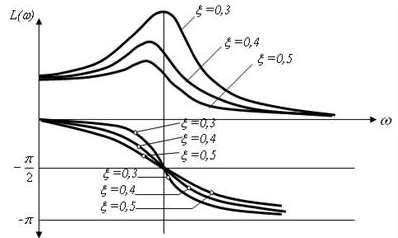
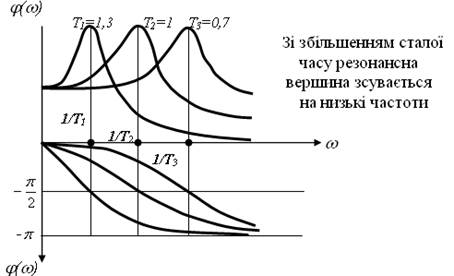
У реальних ланках не можна незалежно змінювати параметри x і Т. Через розширення полоси частот падає коефіцієнт підсилення.

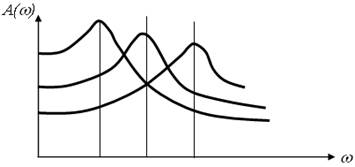
Перехідна функція h(t) має вигляд:

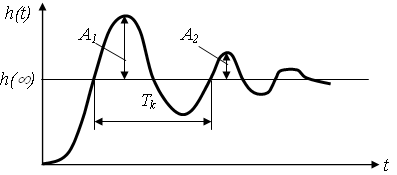
де T_k – період коливань;

A₁, A₂ – амплітуди двох сусідніх коливань відносно значення, яке

встановилося.

7) Консервативна ланка (ξ = 0).

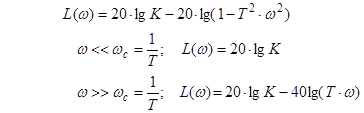
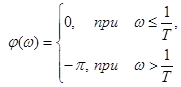
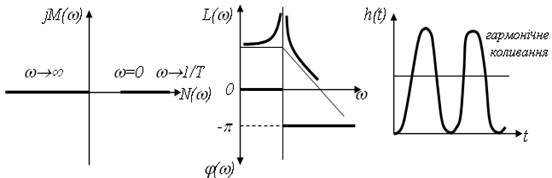
8) Аперіодична ланка другого порядку (ξ ≥ 1).

Передаточну функцію при ξ ≥ 1 можна перетворити до виду:

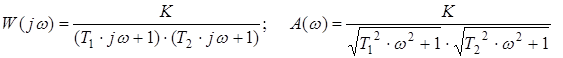
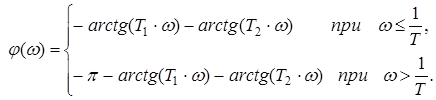
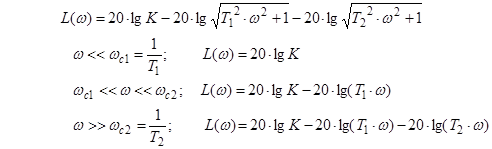
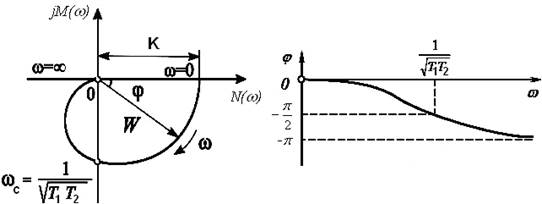
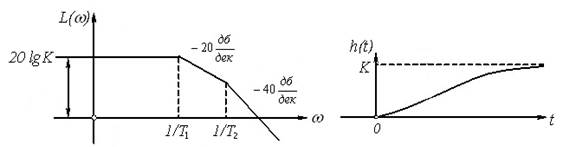
Аперіодичну ланку другого порядку можна уявити як послідовне з’єднання двох аперіодичних ланок першого порядку. Воно не відноситься до числа елементарних ланок.

9) Форсуюча ланка другого порядку

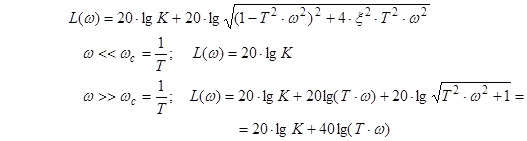
2.4.2 Немінімально-фазові ланки

Ланку називають мінімально-фазовою, якщо всі нулі і полюси цієї передаточної функції мають від’ємні або рівні нулю дійсні частини.

Ланку називають немінімально-фазовою, якщо хоча б один нуль або полюс її передаточної функції має позитивну дійсну частину.

Нулями передаточної функції

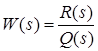, де R(s) і Q(s) – поліноми від s, називають корені рівняння R(s)=0, тобто такі значення s, при яких передаточна функція обертається в нуль, а полюсами – корені рівняння Q(s)=0, тобто такі значення s, при яких передаточна функція обертається в нескінченність.

Всі розглянуті вище елементарні ланки відносять до мінімально-фазових. Прикладами немінімально-фазових елементарних ланок є ланки з передаточними функціями

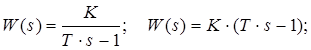
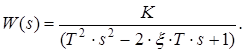
Для немінімально-фазової ланки характерно, що у неї зсув фази по модулю більший, ніж у мінімально-фазової ланки, яка має однакову з немінімально-фазовою ланкою АЧХ.

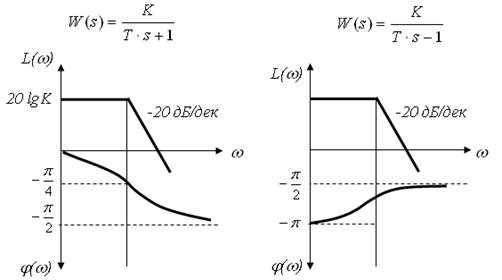
До немінімально-фазових ланок відносять також ланку чистої затримки (хвилевід, трубопровід, довгі лінії) з передаточною функцією

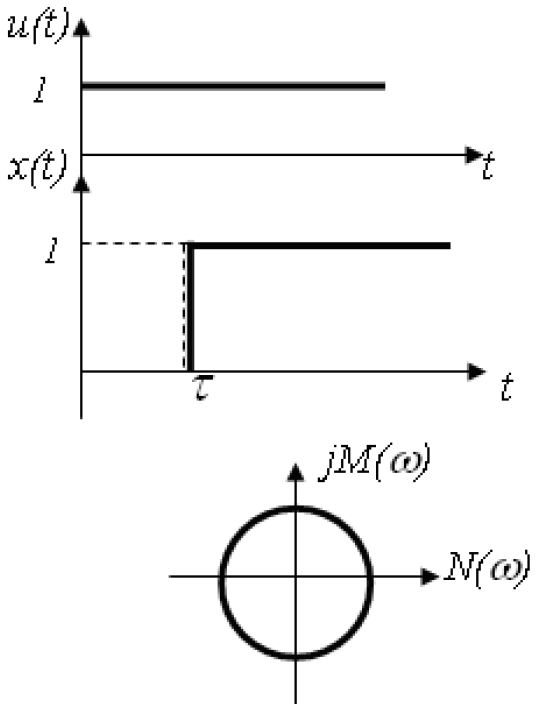
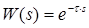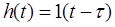
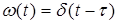
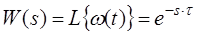
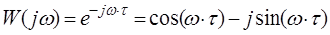
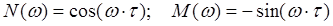
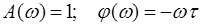
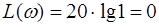
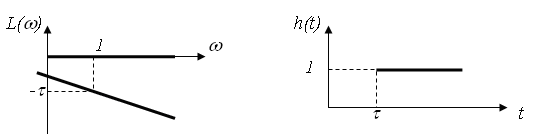
Застосувавши розклад в ряд для експоненти, диференціальне рівняння прийме вигляд

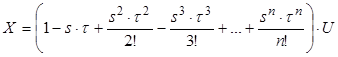2.4.3 З’єднання ланок. Структурні схеми

Розглянемо зєднання ланок та їх структурні схеми:

1) Послідовне з’єднання ланок.

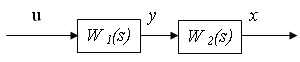
тобто з’єднання 2-х ланок можна представити єдиною ланкою:

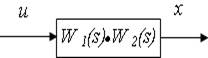
ЛАЧХ з’єднання 2-х ланок дорівнює сумі ЛАЧХ ланок.

2) Паралельне з’єднання ланок.

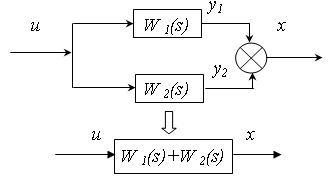
3) Ланка, охоплена зворотним зв’язком (ЗЗ).

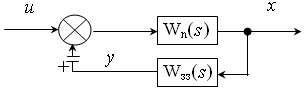
“ – “ для додатнього ЗЗ

“ + ” для від’ємних ЗЗ

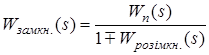
Розглянемо замкнуте коло ланок:

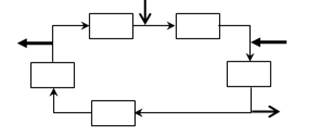
Часто нас цікавлять передаточні функції для одного і того ж контуру, але для різних входів і виходів.

Уявимо замкнене коло ланок у вигляді орієнтованого графа:

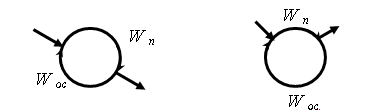
2.4.4 Структурні схеми та їх еквівалентні перетворення

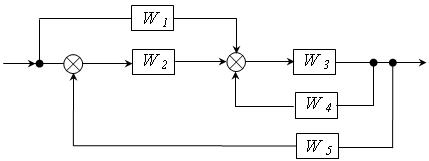
В ЛДС допускається тільки сумування та гілкування, інші операції неможливі. Для отримання передаточної функції довільного з’єднання ланок необхідно за допомогою еквівалентних перетворень привести структурну схему до відомих з’єднань:

− послідовного;

− паралельного;

− зі зворотним зв’язком.

2.4.5 Правила переносу суматора і точки гілкувань крізь блок

1) Перенос вузла суматора по ходу сигналу.

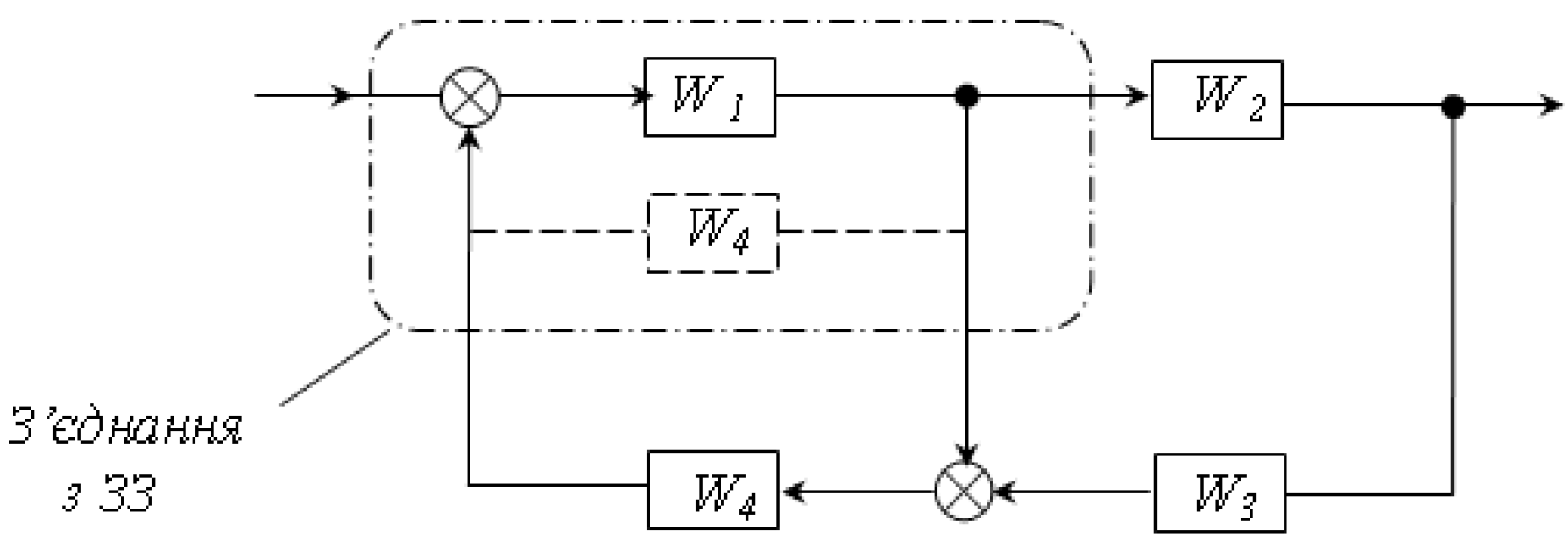
Дослідимо принцип суперпозиції для ЛДС

(А+В)+С=(А+С)+В.

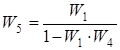2) Перенос суматора проти ходу сигналу.

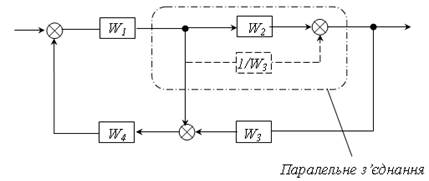
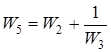Незалежно від способу перетворення передаточна функція системи буде однаковою.

2.4.6 Зворотні зв’язки. Класифікація, практичне застосування

Розглянемо окремі випадки ЗЗ:

1) Операційний підсилювач (ОП):

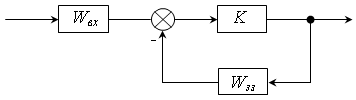
Особливість ОП: K>>1 (K – коефіцієнт підсилення).

Для МН-7: K = 300000; K = 5 – 10 млн.

Зворотний зв’язок від’ємний.

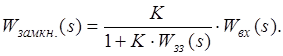
Так як K>>1, відкидаємо 1 Þ .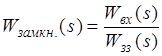

2) Глибокий зворотний зв’язок.

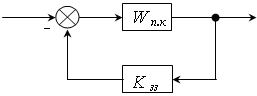
K_зз>>1; .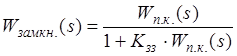

Так як K >> 1, то відкидаємо 1 Þ .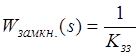

Цей прийом застосовується в підсилювачах потужності. За рахунок глибокого ЗЗ компенсується дрейф, нелінійності прямого кола. Небажані властивості прямого кола не відтворюються в системі. До таких пристроїв відноситься емітерний повторювач.

3) Гнучкий зворотний зв’язок.

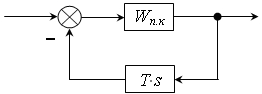
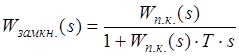
В стані, який встановився t®¥, що відповідає області S®0, тоді

Коефіцієнт ЗЗ залежить від частоти сигналу. При малих частотах ЗЗ відсутній, а на великих частотах ЗЗ існує. Застосовується в електроприводах.

Завдання для самостійного розв’язку

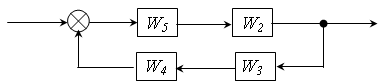
Виконати еквівалентне перетворення наступних схем:

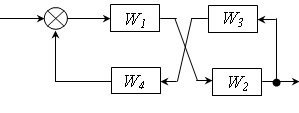
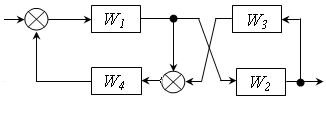
Контрольні питання:

Наведіть принцип перетворення Лапласа.
Довести теорему розкладання.
Довести теорему про згортку.
Довести теорему про граничні значення.
Навести приклад інтерпретації перетворення Лапласа.
Навести властивості перетворення Лапласа.
Реальні ситуації, коли САУ повинна відпрацьовувати деякий програмний сигнал.
Запишіть систему неоднорідних лінійних різницьових рівнянь у матрично-векторному виді.
Запишіть перехідну функцію стану для еквівалентного різницьвого рівняння з ненульовою правою частиною.
Опишіть усталені режими для типових тестових вхідних сигналах.