Попередня сторінка Зміст Наступна сторінка Електронні посібники ВНТУ
3 АНАЛІЗ СТІЙКОСТІ ТА ОЦІНКА ЯКОСТІ РЕГУЛЮВАННЯ НЕПЕРЕРВНИХ САУ
3.1 Проблема стійкості та її сучасні прояви
3.2 Класифікація типів стійкості
3.4 Теореми Ляпунова про стійкість за першим наближенням (про стійкість лінеаризованих систем)
3.5 Алгебраїчні критерії стійкості
3.5.1 Необхідні умови стійкості
3.6 Частотні критерії стійкості
3.6.2 Частотний критерій стійкості Михайлова
3.6.3 Частотний критерій стійкості Найквіста
3.7 Запас стійкості по амплітуді та фазі
3.8 Аналіз стійкості САУ по частотним характеристикам
3.9 Побудова областей стійкості в площині параметрів системи. Метод D-розбиття
3.10 Аналіз стійкості систем з запізненням
3.11 Задача про граничне запізнення
3.12 Оцінка якості регулювання САУ за часовими характеристиками
3.12.1 Непрямі оцінки якості перехідних процесів
3.12.2 Оцінка якості САУ в усталених режимах
3.1 Проблема стійкості та її сучасні прояви
Поняття стійкості відносне : завжди мається на увазі клас обурень; стійкості зовсім не існує.
Пам’ятайте про це.
Стійкість до
- початкових відхилень;
- випадкових обурень;
- відмов частин системи.
Які види стійкості Ви можете ще запропонувати?
- птахостійкість (для літаків);
- “foolpruf ” (дуростійкість);
- стійкість до відмов окремих елементів;
- стійкість до помилок проектування (схованих до певного часу), виробника, експлуатації.
В сучасних САУ та обчислювальних системах ненадійність на 50% обумовлена помилками, які допущені в проекті.
Як же отримати відмовостійкість? Один з магістральних шляхів сьогодні – диверсифікація. В основі диверсифікації лежить проблема розбиття системи на частини – проблема декомпозиції.
Велика і мала наука кружляє навколо розбиття за функціональними ознаками – “колеса, двигун, ресори”, “датчики, приводи, підсилювач”, в той час як сучасні технології уже дозволяють конструювати системи зовсім за іншими принципами: розбити систему на підсистеми, кожна з яких може виконувати всі функції цілої системи, але різноманітними засобами з різноманітним рівнем якості.
Ці декомпозиції можна пояснити простими прикладами.
Уявіть собі: автомобіль під’їхав до лісу, розділився на чотири маленьких автомобільчика, які, проїхавши по лісним стежкам, потім знову зібралися в один автомобіль. Фантастика!? – такий автомобіль представили японці на виставці в 1990 році.
І ще про автомобілі. Уявіть собі автомобіль, в нього відламалось колесо, але він швидко трансформувався в мотоцикл, знову щось вийшло з ладу… і в кінці, Ви спокійно прибуваєте в пункт призначення на велосипеді, зібраному з останків автомобіля. Поки що таке траплялося тільки в мультфільмах.
При традиційному резервуванні, наприклад, дублюванні – просто одна і та ж помилка проектування, програмування повторюється двічі – і “вискакує” одночасно в обох підсистемах !!!
При неідентичному резервуванні передбачається, що можливі помилки неідентичні і взаємокомпенсуються.
Особливість диверсифікації як методу проектування на відміну від відомих раніше “творчих конкурсів” – “не перемагає найсильніший”, а реалізується в паралельних пристроях розробки, яка задовольняє технічне завдання.
Матеріальна основа для диверсифікації – різке зменшення питомої вартості обчислювальної техніки.
Може бути поки що незвичне вирішення проблеми відмовостійкості великих відповідальних САУ. До цього ми повернемося в наступному семестрі. А зараз займемося класичною стійкістю.
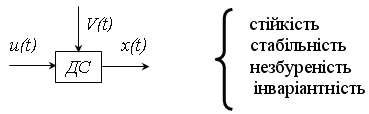
Стійкість – збереження незмінними необхідних значень змінних, не дивлячись на зовнішні впливи, на початкові відхилення.
В 1892 році з’явилася праця А.М. Ляпунова “Загальна задача про стійкість руху”.
3.2 Класифікація типів стійкості
Стійка система, стійка рівновага.
Нестійка система, нестійка рівновага.
Нейтральна стійкість, нейтральна рівновага.
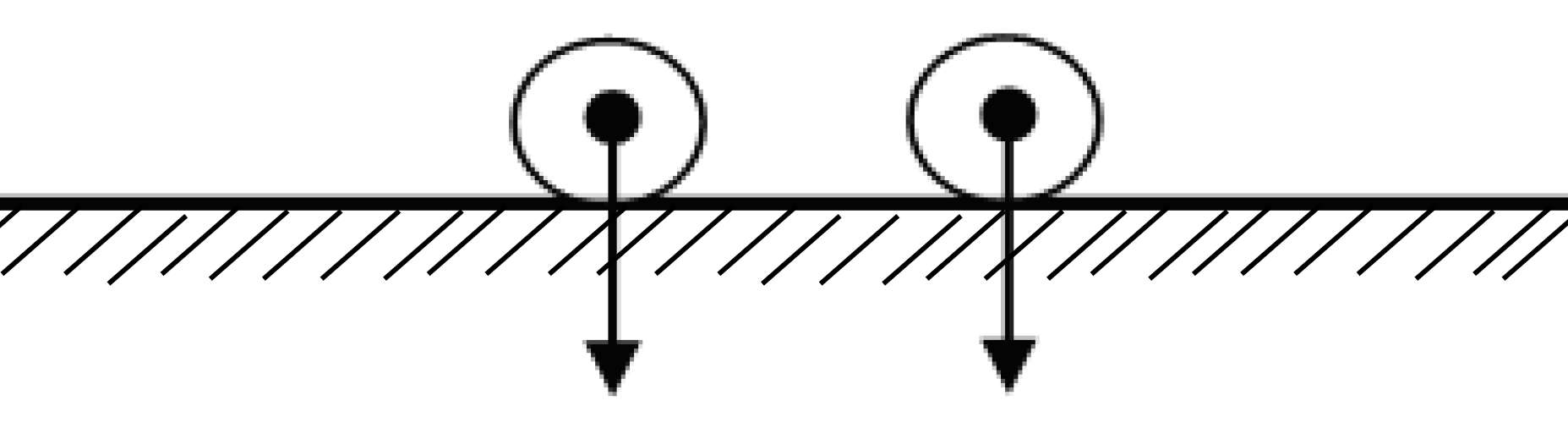
Обмежена стійкість.
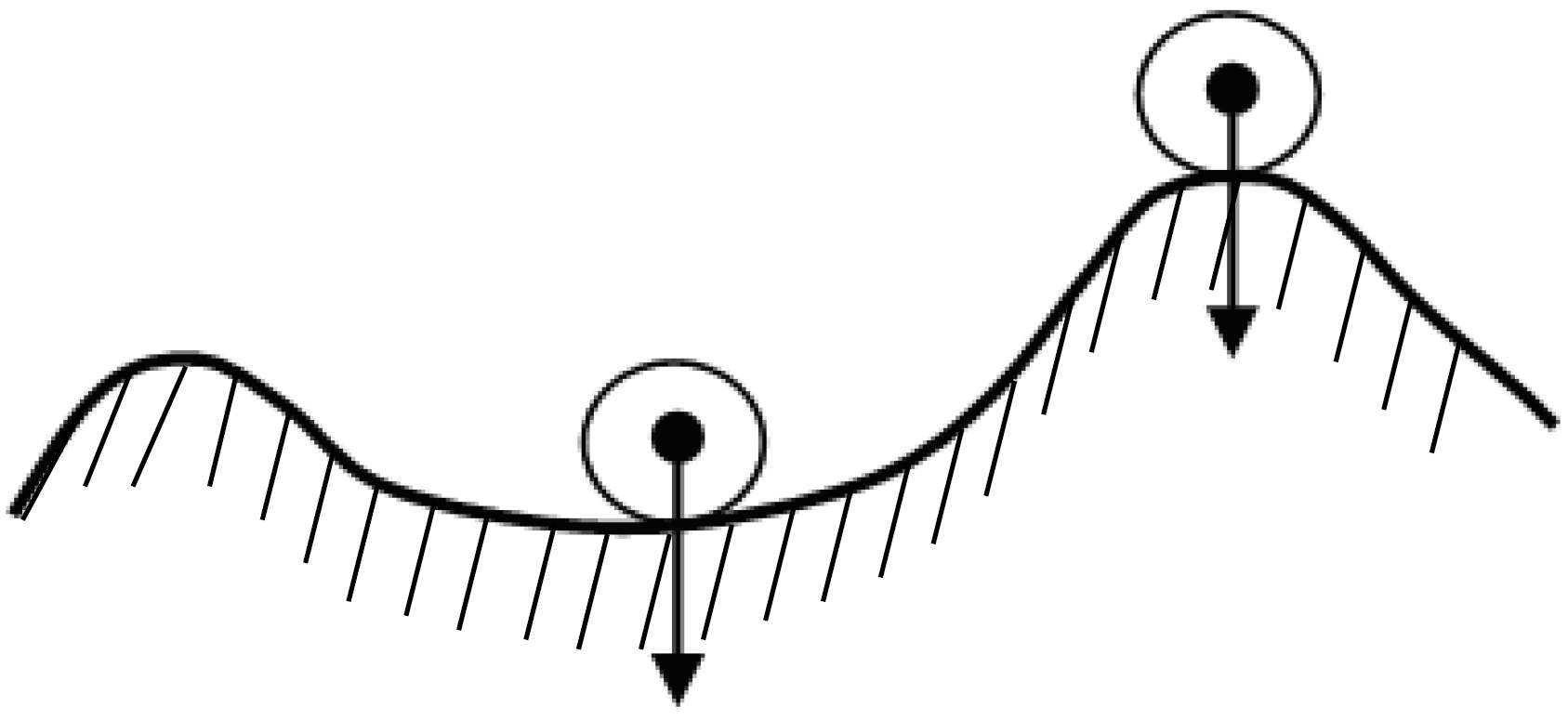
Напівстійкість.
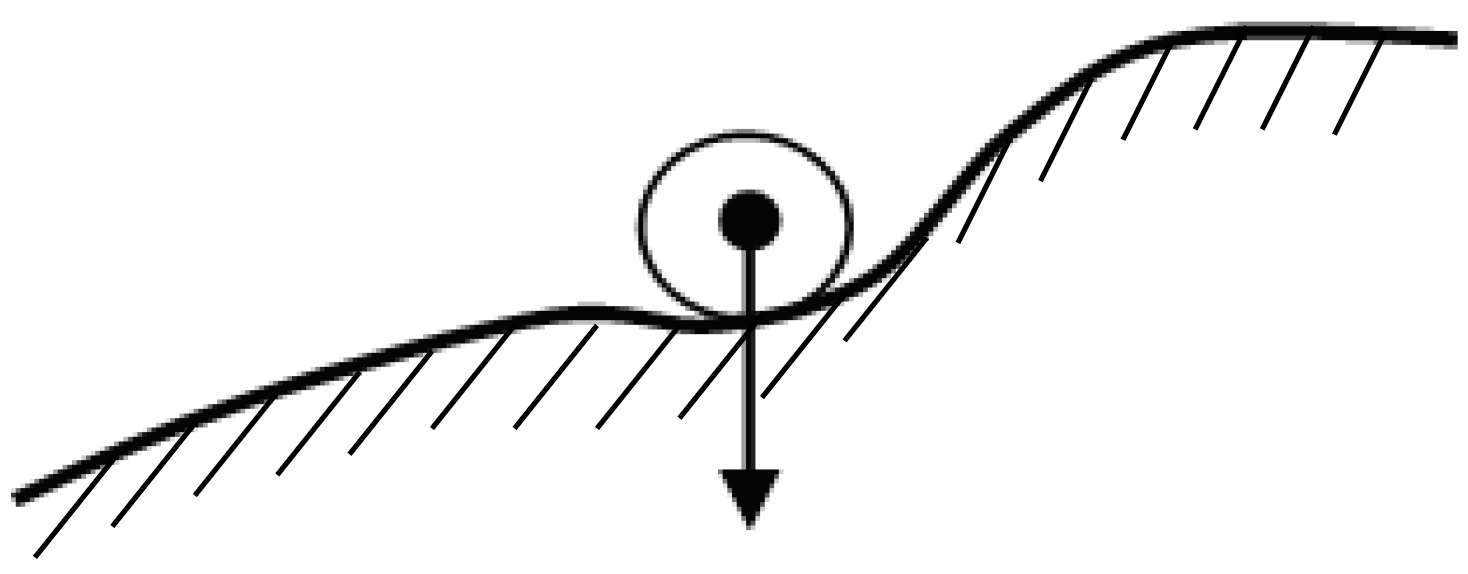
Стійкість Ляпунов класифікував за величиною області стійкості:
- стійкість “в малому”,
- стійкість “в великому”,
- стійкість “в цілому ”.
1. Стійкість “в малому”.
δ - нескінченно мала величина
2. Стійкість “в великому”.
Δ - кінцева величина
3. Cтійкість “в цілому”.
3.3 Збурений і незбурений рух
А.М. Ляпунов запропонував розглядати стійкість тільки по відношенню до відхилення початкових умов.
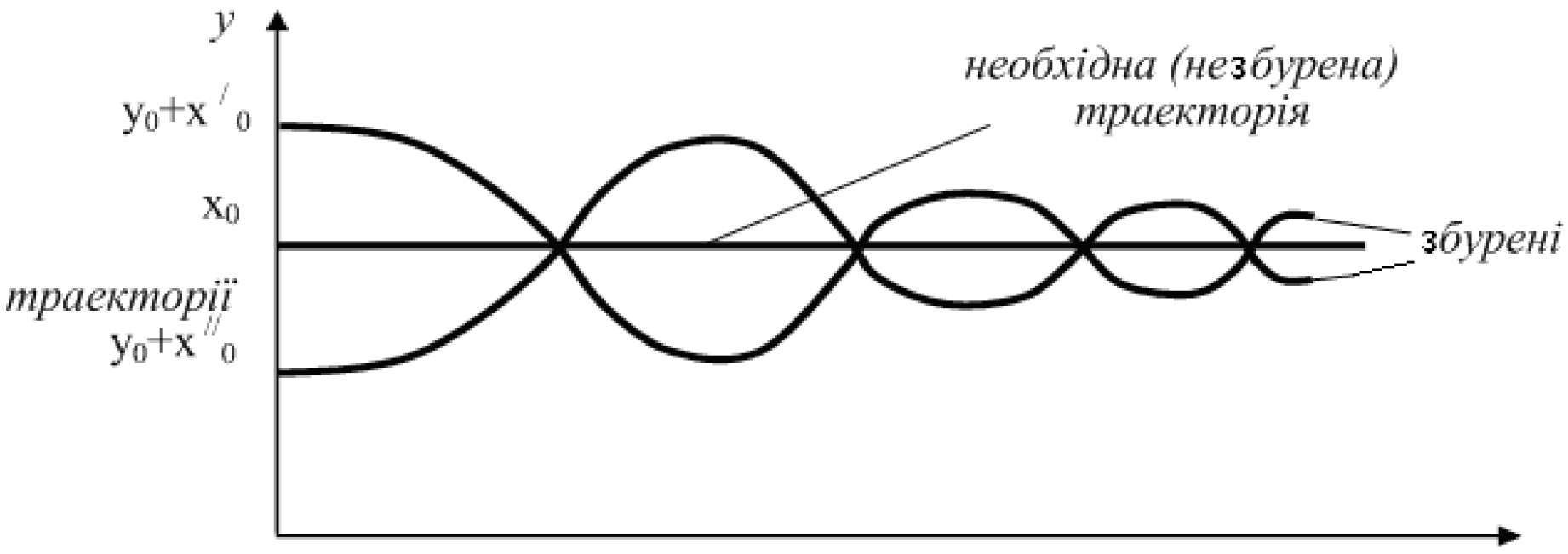
Рисунок 3.1 – Графіки збуреного та незбуреного рухів
Деякий дійсно визначений рух системи, який підлягає дослідженню будемо називати незбуреним (необхідним, опорним, номінальним).
До появи праць А.М. Ляпунова по стійкості, в цій області був ідейний тупий кут – не вдавалося чітко визначити стійкість.
А.М. Ляпунов отримав конструктивні результати, обмежившись розглядом стійкості тільки по відношенню до початкових збурень.
Отже, будемо розглядати поведінку системи при варіаціях початкових умов, а ці варіації будемо вважати малими, що дасть нам право використовувати замість початкових рівнянь лінеаризовані рівняння руху (рівняння першого наближення).
Вибір незбуреного руху проводиться з практичних міркувань.
Визначення стійкості за Ляпуновим має наступне формулювання.
Незбурений рух назвемо стійким по відношенню до змінних ![]() .
.
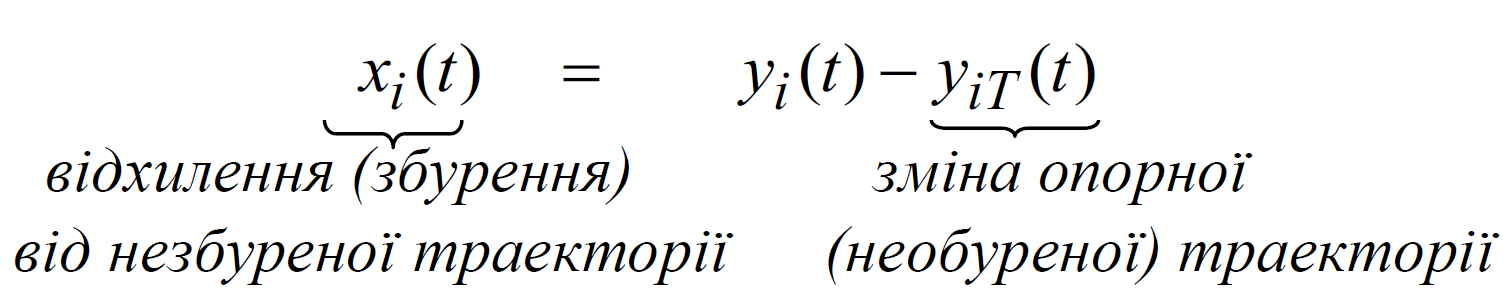
Якщо при будь-якому довільно заданому додатному числі ![]() можна задати інше додатне число
можна задати інше додатне число ![]() так, що при будь-яких збуреннях
так, що при будь-яких збуреннях ![]() , які задовольняють умову
, які задовольняють умову
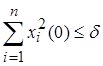
слідує для всіх ![]()
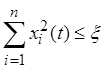 .
.
Визначення Ляпунова має наступну наочну інтерпретацію:
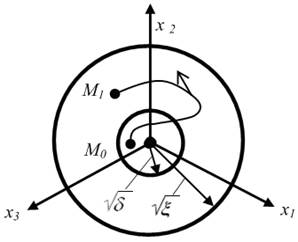
Рисунок 3.2 – Наочна інтерпретація визначення Ляпунова
![]()
![]()
При незбуреному руху ![]() відповідає нерухома точка – початок координат.
відповідає нерухома точка – початок координат.
Виберемо радіус сфери ![]() довільно малим. Якщо незбурений рух стійкий, то для цієї сфери повинна знайтись інша сфера
довільно малим. Якщо незбурений рух стійкий, то для цієї сфери повинна знайтись інша сфера ![]() , яка володіє наступною властивістю: відображаюча точка М, почавши свій рух з будь-якої точки М0, яка лежить усередині або на поверхні сфери
, яка володіє наступною властивістю: відображаюча точка М, почавши свій рух з будь-якої точки М0, яка лежить усередині або на поверхні сфери ![]() , при своєму подальшому русі залишається завжди всередині сфери
, при своєму подальшому русі залишається завжди всередині сфери ![]() .
.
3.4 Теореми Ляпунова про стійкість за першим наближенням (про стійкість лінеаризованих систем)
Лінійну замкнену систему в векторно-матричному вигляді можемо представити як
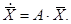
Згадаємо, як знаходиться розв’язок системи лінійних диференціальних рівнянь. Виконаємо перетворення Лапласа
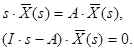 .
.
Позначимо
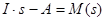 ,
,
тоді побачимо, що ![]() – це в згорнутому вигляді система алгебраїчних рівнянь без правої частини
– це в згорнутому вигляді система алгебраїчних рівнянь без правої частини
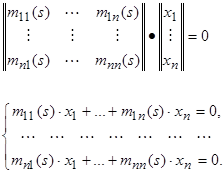
Відомо, що така система однорідних алгебраїчних рівнянь має нетривіальний розв’язок
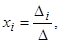
якщо ![]() .
.
З цієї умови існування розв’язання системи рівнянь (4) слідує, що
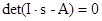
Розкривши визначник, отримаємо алгебраїчне рівняння n-ого степеня відносно змінної s – характеристичного рівняння
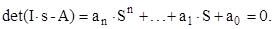
Відомо, що розв’язання системи диференціальних рівнянь записується через корені характеристичного рівняння наступним чином
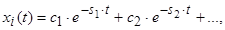
де ![]() – корені характеристичного рівняння,
– корені характеристичного рівняння, ![]() .
.
Сформулюємо теореми.
Теорема 1.
Якщо дійсні частини всіх коренів характеристичного рівняння
![]() від’ємні,
від’ємні,
то незбурений рух асимптотично стійкий.
Теорема 2.
Якщо серед коренів характеристичного рівняння ![]() ,
,![]() буде хоча б
буде хоча б
один, у якого ![]() ,
,
то незбурений рух нестійкий.
Розглянемо умови стійкості лінійних систем.
Переформулюємо результати А.М. Ляпунова в більш сучасному вигляді:
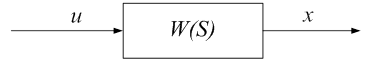
Рисунок 3.3 – Структурна схема динамічної одновимірної системи
Використовуючи перетворення Лапласа, рівняння динаміки для лінійної однорідної системи запишемо в наступному вигляді
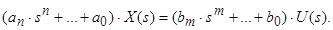
Характеристичне рівняння
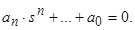
Аналогічно може бути отримане характеристичне рівняння для багатомірної системи (як це було показано при розгляді стійкості за першим наближенням):
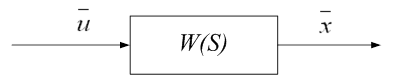
Рисунок 3.4 – Отримання результату для багатомірної системи
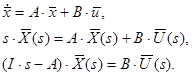
У відповідності з визначенням стійкості за теоремою Ляпунова (під стійкістю розуміється стійкість вільного руху) розглядаємо рух правої частини
![]() .
.
Для нетривіального розв’язання
![]() ,
,
що дає нам характеристичне рівняння.
Таким чином, методи аналізу стійкості однорідної та багатомірної системи єдині.
Необхідною і достатньою умовою стійкості ЛДС є від’ємність дійсних частин всіх коренів характеристичного рівняння системи ![]() ,
, ![]() ,тобто всі корні характеристичного рівняння повинні бути “лівими”.
,тобто всі корні характеристичного рівняння повинні бути “лівими”.
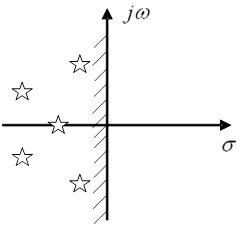
Проблема стійкості ЛДС еквівалентна відокремленню коренів полінома.
3.5 Алгебраїчні критерії стійкості
Вірні обидва твердження: “Якщо корені ліві – система стійка”,
“Якщо система стійка – корені ліві”
3.5.1 Необхідні умови стійкості
За теоремою Безу:
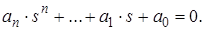
Також можна виразити за допомогою коренів:
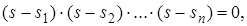
де ![]() – корені характеристичного рівняння.
– корені характеристичного рівняння.
Можна записати :
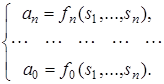
Існує взаємооднозначна відповідність між коренями і коефіцієнтами. Можна довести наступне твердження:
Якщо всі корені мають від’ємні дійсні частини (уявні корені тільки
спряжені),
то коефіцієнти ![]() , тобто
, тобто ![]() .
.
Англійський математик Е. Раус в 1877 році і німецький математик А. Гурвиць в 1895 році винайшли спосіб, не знаходячи корені, опрацювати необхідні і достатні умови ЛДС.
Критерії Рауса і Гурвиця можна опрацювати самостійно (Воронов А.А., ТАУ, Ч. 1. – М.: Высшая школа, 1986. – C. 128-137).
Раус запропонував критерій стійкості САУ у вигляді алгоритму за яким заповнюється спеціальна таблиця, в якій записуються коефіцієнти характеристичного полінома. Правила для побудови таблиці такі:
- в першому рядку записуються коефіцієнти рівняння з парними індексами в порядку їх спадання;
- у другому рядку — з непарними;
- інші елементи таблиці визначаються за формулою
![]()
![]() ,
,
де 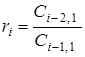 ,
, ![]() ,
,
![]() — номер рядка,
— номер рядка,
![]() — номер стовпця.
— номер стовпця.
Число рядків таблиці Рауса на одиницю більше порядку характеристичного рівняння.
Для того, щоб САУ була стійкою необхідно і достатньо, щоб коефіцієнти першого стовпця таблиці Рауса були додатними. Якщо умова не виконується, то система нестійка.
До переваг методу відноситься проста реалізація на ЕОМ, а також простота аналізу для систем невеликого (до третього) порядку.
До недоліків можна віднести ненаглядність методу, оскільки по ньому складно судити про ступінь стійкості, про її запас
Таблиця 3.1 – Таблиця Рауса
|
|
|
1 | 2 | 3 |
|---|---|---|---|---|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
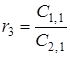
|
3 |
|
|
|
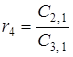
|
4 |
|
|
|
|
|
|
… |
… |
… |
Приклад: використовуючи критерій Рауса, визначити чи стійка ЛДС, якщо характеристичне рівняння має вигляд
![]() .
.
![]() , де
, де ![]() − порядок системи.
− порядок системи.
| Значення | Номер рядка | Номер стовпця | |||
| 1 | 2 | 3 | 4 | ||
| - | 1 |
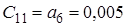
|
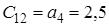
|
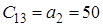
|
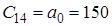
|
| - | 2 |
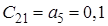
|
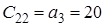
|
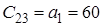
|
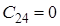
|
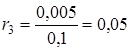
|
3 |
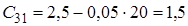
|
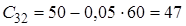
|
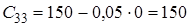
|
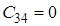
|
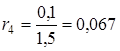
|
4 |
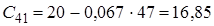
|
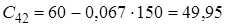
|
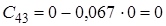
|
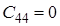
|
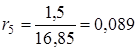
|
5 |
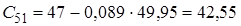
|
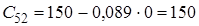
|
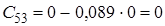
|
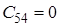
|
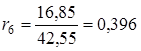
|
6 |
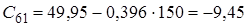
|
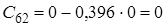
|
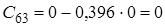
|
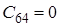
|
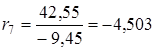
|
|
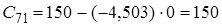
|
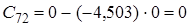
|
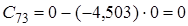
|
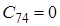
|
![]() Оскільки
Оскільки ![]() , тобто не всі коефіцієнти першого стовпця таблиці Рауса додатні, то така система буде нестійка.
, тобто не всі коефіцієнти першого стовпця таблиці Рауса додатні, то така система буде нестійка.
Дано: характеристичне рівняння ЛДС
![]()
Необхідно визначити: чи стійка дана ЛДС ?
Розв’язання:
1) Складається головний визначник Гурвиця за правилом: коефіцієнти розміщуємо по головній діагоналі, починаючи з ![]() . Останній стовпець має один ненульовий коефіцієнт.
. Останній стовпець має один ненульовий коефіцієнт.
Визначник порядку ![]() має вигляд:
має вигляд:
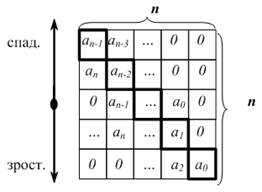
2) Послідовно виділяємо (викреслюємо стрічки і стовпці) визначники Гурвиця:
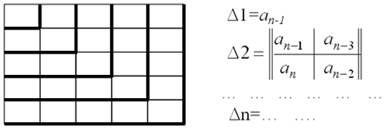
Система необхідно і достатньо стійка, якщо для всіх ![]()
![]() ,
, 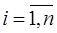 . Всі
. Всі ![]() визначників Гурвиця тільки додатні.
визначників Гурвиця тільки додатні.
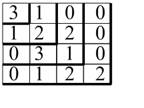
Приклад: використовуючи критерій Гурвиця, визначити чи стійка ЛДС, якщо характеристичне рівняння має вигляд
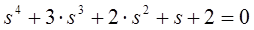 .
.
![]() , де
, де ![]() − порядок системи.
− порядок системи.
![]()
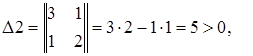
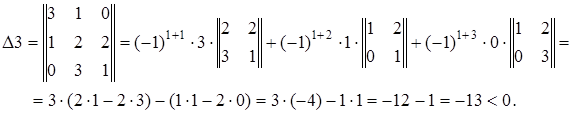
Система нестійка, оскільки ![]() .
.
Завдання для самостійного рішення
Перевірити чи стійка ЛДС, якщо :
1) -5s5-4s4-3s3-2s2-s-20=0
2) 7s7+6s6+4s4+3s3+2s2+s=0
3.6 Частотні критерії стійкості
Неформалізована постановка задачі
![]() Навіщо власне необхідні частотні характеристики ?
Навіщо власне необхідні частотні характеристики ?
Щоб зрозуміти це, спробуйте відповісти на питання :
![]() ”Якою інформацією про реальний об’єкт володіє інженер, досліджуючи САУ на стійкість ?”
”Якою інформацією про реальний об’єкт володіє інженер, досліджуючи САУ на стійкість ?”
Згадаєте, як космонавти пригали і бігали всередині космічної станції “Салют”, щоб отримати характеристики її пружніх коливань.
Частотні характеристики зручні тим, що використовують безпосередньо експериментальні данні.
![]() Вам необхідно знайти критерії стійкості, в яких би використовувались в якості початкових данних частотні характеристики.
Вам необхідно знайти критерії стійкості, в яких би використовувались в якості початкових данних частотні характеристики.
Постановка учбової проблеми
Давайте уявимо, що частотні критерії невідкриті, і Вам потрібно в короткий термін знайти їх, використовуючи раніше отримані знання, які ми вже знаємо і застосовуємо.
1) Сформулюйте необхідну і достатню умову стійкості ЛДС.
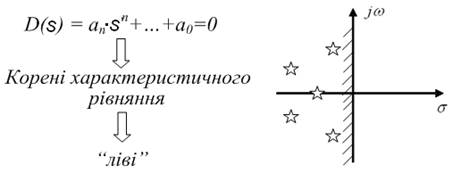
Рисунок 3.5 – Необхідна і достатня умова стійкості ЛДС
2) Згадайте, що таке характеристичне рівняння замкненої САУ? Як воно зв’язане з передаточною функцією?
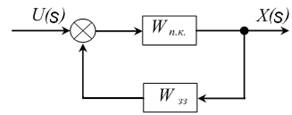
Рисунок 3.6 – Структурна схема замкненої системи
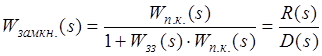 − після алгебраїчних перетворень.
− після алгебраїчних перетворень.
![]() – характеристичне рівняння замкненої САУ.
– характеристичне рівняння замкненої САУ.
Завдання для самостійного рішення
Доведіть, що D(S)=R(S)+Q(S), де R(S) і Q(S) – чисельник і знаменник передаточної функції розімкненої системи : ![]()
3) Як зв’язані частотні характеристики A(w) і j(w) з передаточною функцією W(S) ?
A(w)=mod (W(jw))
j(w)=arg (W(jw))
В чому полягає формальний прийом отримання ЧХ по передаточній функції ? Підставити в W(S) : S=jw.
Давайте розглянемо більш вузьке формулювання учбової проблеми.
Як відображається на частотних характеристиках те, що :
а) всі n корені – ліві;
б) існує l правих коренів ?
Дано: характеристичний поліном
![]() .
.
Необхідно знайти: зв’язок між коренями і ЧХ.
Розв’язання:
Давайте виразимо ![]() за допомогою коренів (за теоремою Безу):
за допомогою коренів (за теоремою Безу):
![]() .
.
А тепер, використаємо знання № 3 (підставляємо ![]() ):
):
![]() .
.
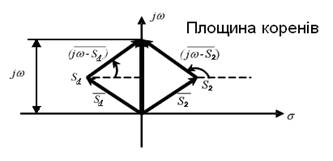
Рисунок 3.7 – Площина коренів
Корінь ![]() можна уявити вектором
можна уявити вектором ![]() . Кожен вектор характеризується модулем і фазовим кутом.
. Кожен вектор характеризується модулем і фазовим кутом.
![]()
Домовимося вважати обертання проти годинникової стрілки додатним. Тоді при зміні ![]() від
від ![]() до
до ![]() кожен елементарний вектор
кожен елементарний вектор ![]() повернеться на кут
повернеться на кут ![]() , якщо його початок, тобто корінь
, якщо його початок, тобто корінь ![]() , розташований зліва від уявної вісі та на кут –
, розташований зліва від уявної вісі та на кут –![]() , якщо корінь розташований справа від уявної вісі.
, якщо корінь розташований справа від уявної вісі.
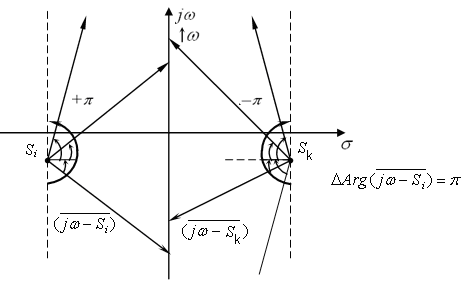
Рисунок 3.8 – Результат зміни ![]() від
від ![]() до
до ![]()
Чому дорівнює приріст аргумента вектора ![]() при умові, що корені ліві?
при умові, що корені ліві?
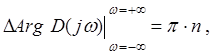
де ![]() – ліві.
– ліві.
Нехай порядок системи ![]() , число правих коренів –
, число правих коренів – ![]() , тоді число лівих коренів
, тоді число лівих коренів ![]() . Для цього загального випадку
. Для цього загального випадку
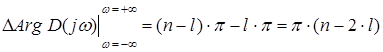 .
.
Годограф вектора ![]() при зміні
при зміні ![]() від 0 до
від 0 до ![]() дозволяє визначати наявність або відсутність правих коренів. Частотні критерії як і алгебраїчні являють собою часткові рішення загальної проблеми – відокремлення коренів характеристичного рівняння.
дозволяє визначати наявність або відсутність правих коренів. Частотні критерії як і алгебраїчні являють собою часткові рішення загальної проблеми – відокремлення коренів характеристичного рівняння.
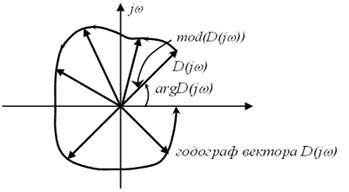
Рисунок 3.9 – Годограф вектора ![]()
3.6.2 Частотний критерій стійкості Михайлова
Цей критерій стійкості, сформульований в 1938 році радянським вченим А.В. Михайловим, є по суті геометричною інтерпретацією принципу аргумента.
Дано: характеристичний поліном
![]() .
.
Необхідно: перевірити дану САУ на стійкість.
Розв’язання:
1) Робимо підстановку: ![]()
![]()
2) Виділяємо дійсну та уявну частини полінома ![]() :
:
![]()
де ![]() – дійсна функція Михайлова;
– дійсна функція Михайлова;
![]() – уявна функція Михайлова.
– уявна функція Михайлова.
3) Складаємо таблицю:
|
|
|
|
|
0 |
|
0 |
|
1 |
0,7 |
0,1 |
|
5 |
2,3 |
−2 |
|
… |
… |
… |
|
|
… |
… |
4) За таблицею будуємо годограф вектора ![]() – годограф Михайлова.
– годограф Михайлова.
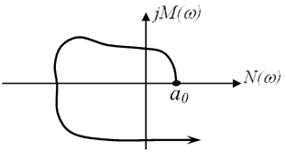
Рисунок 3.10 – Годограф Михайлова
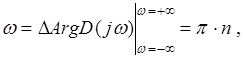
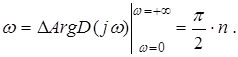
Будемо розглядати зміну частоти від 0 до ¥, тому що АФЧХ симетрична, а також достатньо побудувати половину АФЧХ, а на практиці АФЧХ може бути знята для додатних частот.
Сформулюємо критерій стійкості Михайлова.
Для того, щоб САУ була стійкою необхідно і достатньо, щоб годограф Михайлова при зміні частоти від 0 до ![]() , починаючись на дійсній додатній піввісі при
, починаючись на дійсній додатній піввісі при ![]() , послідовно обходив проти годинникової стрілки, ніде не обертаючись в нуль, послідовно
, послідовно обходив проти годинникової стрілки, ніде не обертаючись в нуль, послідовно ![]() квадрантів координатної площини, де
квадрантів координатної площини, де ![]() − порядок системи.
− порядок системи.
Годограф Михайлова для стійких систем має звичайну плавну спіралеподібну форму, при чому кінець її наближається до нескінченності в тому квадранті координатної площини, номер якого дорівнює порядку системи. На рисунку можна побачити типові годографи Михайлова для стійких систем відповідно 1,…,5 порядку.
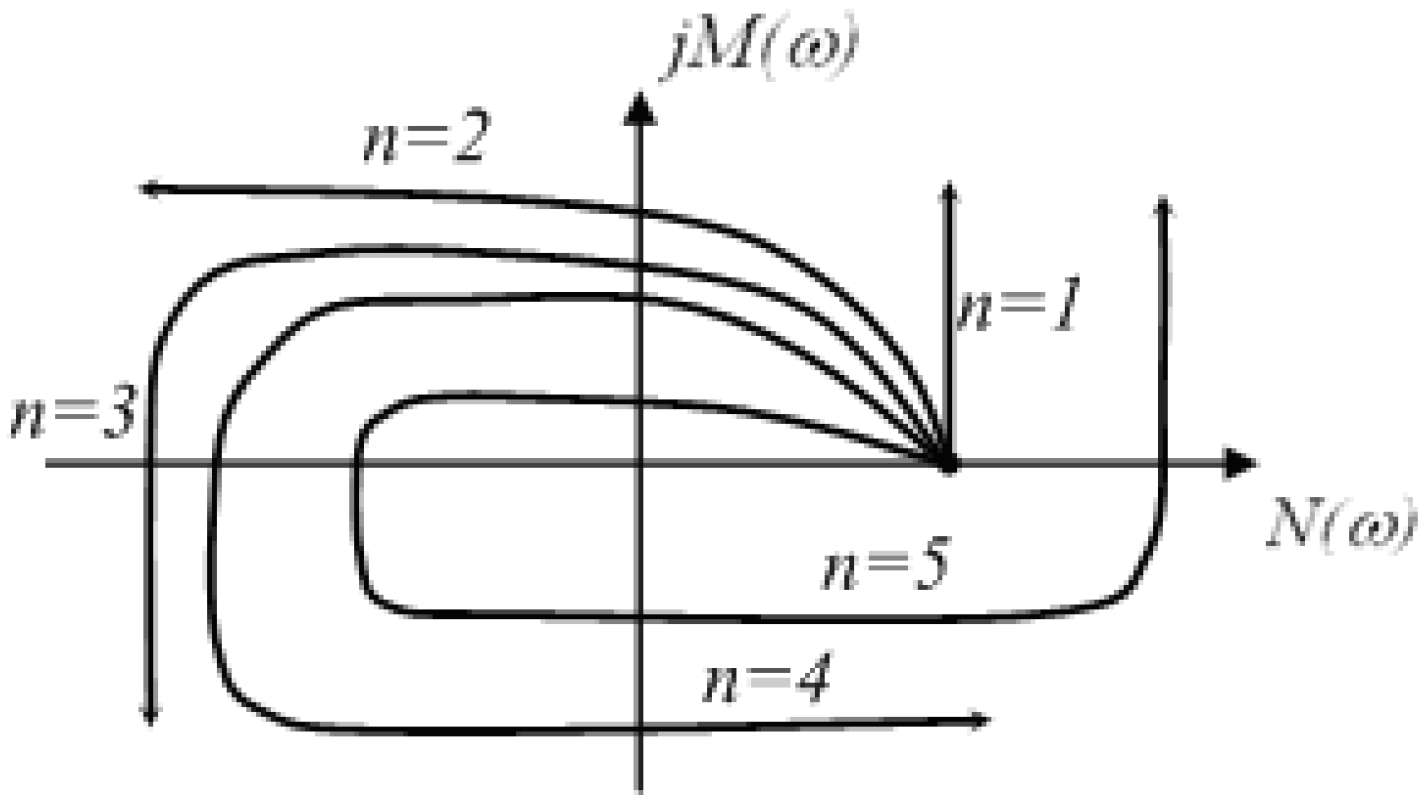
Рисунок 3.11 – Типові годографи Михайлова для стійких систем
Ознакою нестійкості системи є порушення кількості і послідовності пройдених годографом Михайлова квадрантів координатної площини.
![]() Яким системам (стійким чи нестійким) відповідають приведені нижче годографи Михайлова ?
Яким системам (стійким чи нестійким) відповідають приведені нижче годографи Михайлова ?
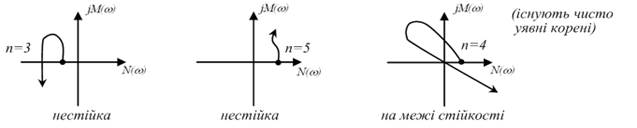
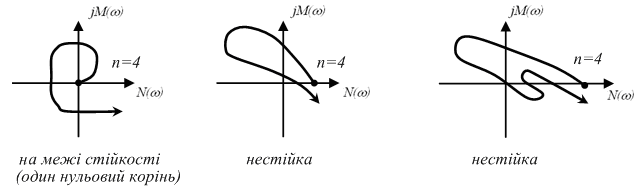
Самостійно !!! Наслідок критерія Михайлова. (Воронов А.А.,ТАУ,ч.I,1986, стор. 143-145).
Завдання для самостійного виконання
Виконати структурні перетворення схеми і знайти передаточну функцію системи.
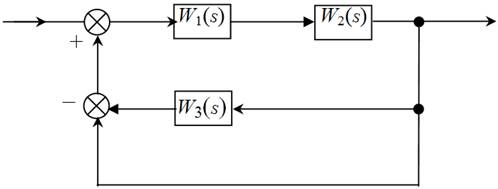
3.6.3 Частотний критерій стійкості Найквіста
Цей критерій запропонований в 1932 році американським вченим Г. Найквістом. Критерій дозволяє аналізувати стійкість замкненої системи по виду АФЧХ розімкненої системи в багатьох випадках отриманої експериментально.
Дано:
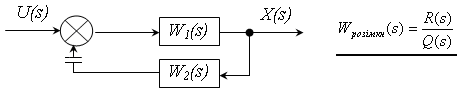
Необхідно визначити: чи стійка замкнена САУ ?
Розв’язання:
![]()
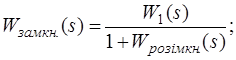
![]() – характеристичний поліном розімкненої системи;
– характеристичний поліном розімкненої системи;
![]() – характеристичний поліном замкненої системи;
– характеристичний поліном замкненої системи;
![]() – рівняння, еквівалентне характеристичному рівнянню замкненої САУ.
– рівняння, еквівалентне характеристичному рівнянню замкненої САУ.
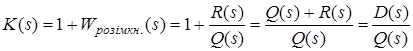 .
.
Оскільки в реальних системах степінь полінома ![]() не вище степені полінома
не вище степені полінома ![]() , тобто
, тобто ![]() , то степінь поліномів
, то степінь поліномів ![]() і
і ![]() однакова і рівна
однакова і рівна ![]() .
.
Підставимо у вираз ![]()
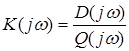 .
.
Розглянемо випадок, який найбільш часто зустрічається, коли розімкнена САУ стійка, тобто всі корені “ліві”.
При зміні частоти ![]() від
від ![]() до
до ![]() зміна кута повороту
зміна кута повороту ![]() на основі принципу аргументу має вигляд
на основі принципу аргументу має вигляд
![]() .
.
Це означає, що для стійкої замкненої системи необхідно, щоб АФЧХ ![]() не охоплювала початок координат, а АФЧХ
не охоплювала початок координат, а АФЧХ ![]() не охоплювала точку
не охоплювала точку ![]() .
.
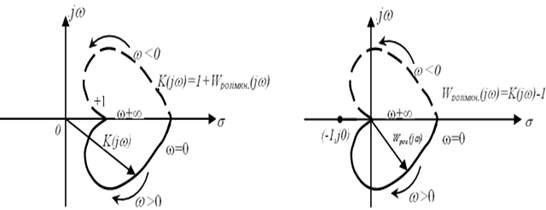
Рисунок 3.12 – Годографи ![]() та
та ![]()
Таким чином, отримаємо наступне формулювання критерію Найквіста.
Якщо розімкнена САУ стійка, то замкнена САУ буде стійка, якщо АФЧХ розімкненої системи ![]() не охоплює точку
не охоплює точку ![]() .
.
3.7 Запас стійкості по амплітуді та фазі
В реальних САУ всі параметри мають деяке допустиме розкидання. Зазвичай необхідно, щоб САУ була стійкою при допустимому розкиданні параметрів. Для цієї мети використовується поняття запасів стійкості САУ, які вводяться на основі частотного критерію Найквіста.
Запаси стійкості характеризують віддалення частотного годографа розімкненої системи ![]() від критичної точки з координатами
від критичної точки з координатами ![]() .
.
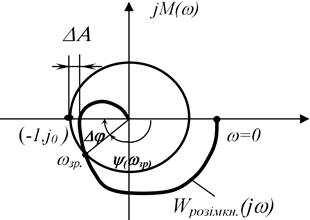
Рисунок 3.13 – Визначення запасів стійкості по амплітуді та фазі
Частота перетину годографа ![]() і одиничного кола називається частотою зрізу
і одиничного кола називається частотою зрізу ![]() . На частоті зрізу
. На частоті зрізу
![]() .
.
Запас стійкості по фазі визначають як величину кута
![]() .
.
Запас стійкості по амплітуді визначають як величину відрізка вісі абсцис ![]() , який знаходиться між критичною точкою
, який знаходиться між критичною точкою ![]() і АФЧХ розімкненої САУ
і АФЧХ розімкненої САУ ![]() .
.
Зі зростанням коефіцієнту підсилення розімкненої системи модуль амплітудно-фазової характеристики також зростає і при деякому значенні коефіцієнта підсилення ![]() ., який називається критичним коефіцієнтом підсилення, АФЧХ пройде крізь точку
., який називається критичним коефіцієнтом підсилення, АФЧХ пройде крізь точку ![]() , тобто система буде на межі стійкості. При
, тобто система буде на межі стійкості. При ![]() система буде нестійкою.
система буде нестійкою.
Однак, зустрічаються системи (з внутрішніми зворотними зв’язками), в яких втрата стійкості може статися не тільки при збільшенні коефіцієнта підсилення, але й при його зменшенні. Цим випадкам можуть відповідати так звані дзьобоподібні АФЧХ.
У цих випадках запас стійкості по амплітуді визначається величинами двох відрізків ![]() вісі абсцис, які знаходяться між критичною точкою
вісі абсцис, які знаходяться між критичною точкою ![]() і АФЧХ.
і АФЧХ.
Щоб система мала необхідний запас стійкості при заданих величинах ![]() і
і ![]() , біля критичної точки
, біля критичної точки ![]() викреслюється деяка заборонена область у вигляді сектора, обмеженого величинами
викреслюється деяка заборонена область у вигляді сектора, обмеженого величинами ![]() і
і ![]() , в яку АФЧХ
, в яку АФЧХ ![]() не повинна входити.
не повинна входити.
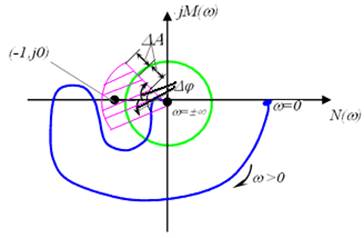
Рисунок 3.14 – Визначення запасів стійкості для випадку дзьобоподібного годографа
Завдання для самостійного рішення
Описати формально запаси стійкості по амплітуді і фазі, Якщо Wрозімкн.(jw) має слідуючий вигляд :
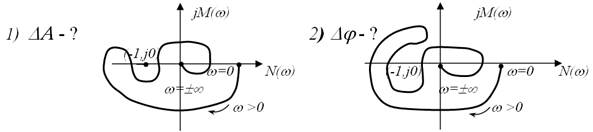
3.8 Аналіз стійкості САУ по частотним характеристикам
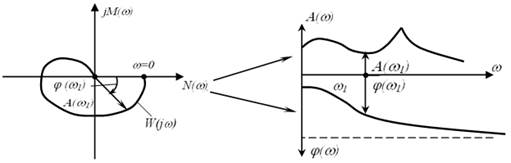
Рисунок 3.15 – Аналіз стійкості за ЛЧХ
Для аналізу стійкості зручно використовувати ЛЧХ. Це обумовлено тим, що побудова ЛЧХ розімкнених систем значно простіша за побудову годографа АФЧХ.Стійкість зв’язана з кількістю переходів АФЧХ ![]() відрізку
відрізку ![]() від’ємної дійсної піввісі.
від’ємної дійсної піввісі.
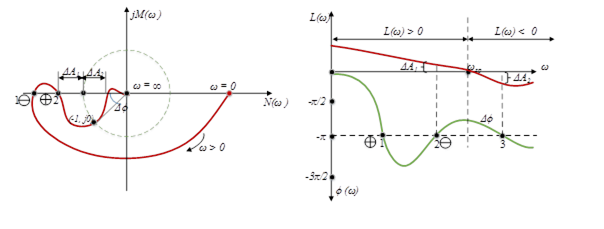
Рисунок 3.16 – Аналіз стійкості за ЛЧХ
Коли ![]() перетинає від’ємну дійсну піввісь, ЛФЧХ перетинає одну з ліній
перетинає від’ємну дійсну піввісь, ЛФЧХ перетинає одну з ліній ![]() Переходи через ці лінії безпечні з точки зору стійкості, якщо вони відбуваються справа від точки
Переходи через ці лінії безпечні з точки зору стійкості, якщо вони відбуваються справа від точки ![]() , тобто якщо
, тобто якщо ![]() .
.
Додатному переходу (зверху вниз) через відрізок ![]() АФЧХ відповідає перетин ЛФЧХ при
АФЧХ відповідає перетин ЛФЧХ при ![]() прямих
прямих ![]() знизу вгору (точка 2), а від’ємному переходу – зверху вниз (точка 1).
знизу вгору (точка 2), а від’ємному переходу – зверху вниз (точка 1).
Критерій стійкості Найквіста стосовно до ЛЧХ може бути сформульований наступним чином.
Якщо розімкнена САУ стійка (всі корені ліві), то замкнена САУ необхідно і достатньо стійка, якщо різниця між кількістю додатних і від’ємних переходів ЛФЧХ прямих ![]() при
при ![]() дорівнює 0.
дорівнює 0.
3.9 Побудова областей стійкості в площині параметрів системи. Метод D-розбиття
Параметри САУ можуть в процесі функціонування системи змінюватись. (Чому? – старіння, дрейф, специфіка; зміна зовнішнього середовища – температура, тиск тощо). Тому побудова областей стійкості САУ в просторі її параметрів, представляє велику цінність.
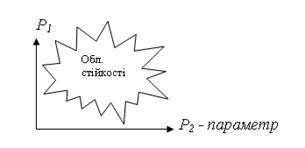
Рисунок 3.17 – Область стійкості за параметрами P1 та P2
Сьогодні таку задачу вирішують на ЕОМ, безпосередньо визначаючи стійкість САУ при різноманітних варіаціях параметрів.
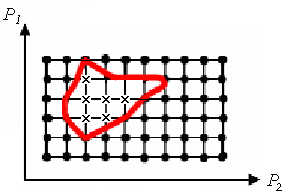
Рисунок 3.18 – Сітка параметрів для визначення області стійкості
× – САУ стійка.
У підручниках описаний докомп’ютерний, але дуже елегантний метод побудови областей стійкості – метод D-розбиття, який був запропонований Ю.М. Неймарком.
У зв’язку з домінуванням прямих комп’ютерних методів, значення методу D-розбиття дещо знизилось.
Метод D-розбиття. Розглянемо основи методу, з яким більш детально рекомендується ознайомитися по підручнику Воронова (частина 1, стор. 155-167) самостійно.
Розглянемо характеристичне рівняння
Уявимо собі ![]() -мірний простір, по координатним вісям якого відкладені коефіцієнти рівняння (3.12). Цей простір називають простором коефіцієнтів.
-мірний простір, по координатним вісям якого відкладені коефіцієнти рівняння (3.12). Цей простір називають простором коефіцієнтів.
Рівняння (3.12) має ![]() коренів, розміщення яких на комплексній площині коренів
коренів, розміщення яких на комплексній площині коренів ![]() , залежить від чисельних значень коефіцієнтів
, залежить від чисельних значень коефіцієнтів ![]() .
.
Якщо змінювати коефіцієнти ![]() рівняння (3.12), то його корені в силу їх неперервної залежності від коефіцієнтів будуть переміщуватись в комплексній площині коренів, описуючи кореневі годографи.
рівняння (3.12), то його корені в силу їх неперервної залежності від коефіцієнтів будуть переміщуватись в комплексній площині коренів, описуючи кореневі годографи.
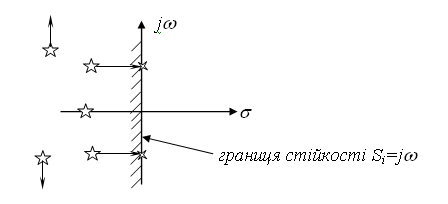
Рисунок 3.19 – Кореневий годограф
Підставимо в рівняння (3.15) вираз ![]() :
:
Це рівняння є початковим для побудови меж стійкості в області параметрів. Якщо проводиться розбиття по одному параметру ![]() , то межа D-розбиття визначається рівнянням
, то межа D-розбиття визначається рівнянням
![]() .
.
Якщо проводиться D-розбиття по двом параметрам ![]() та m, то
та m, то
![]() .
.
3.10 Аналіз стійкості систем з запізненням
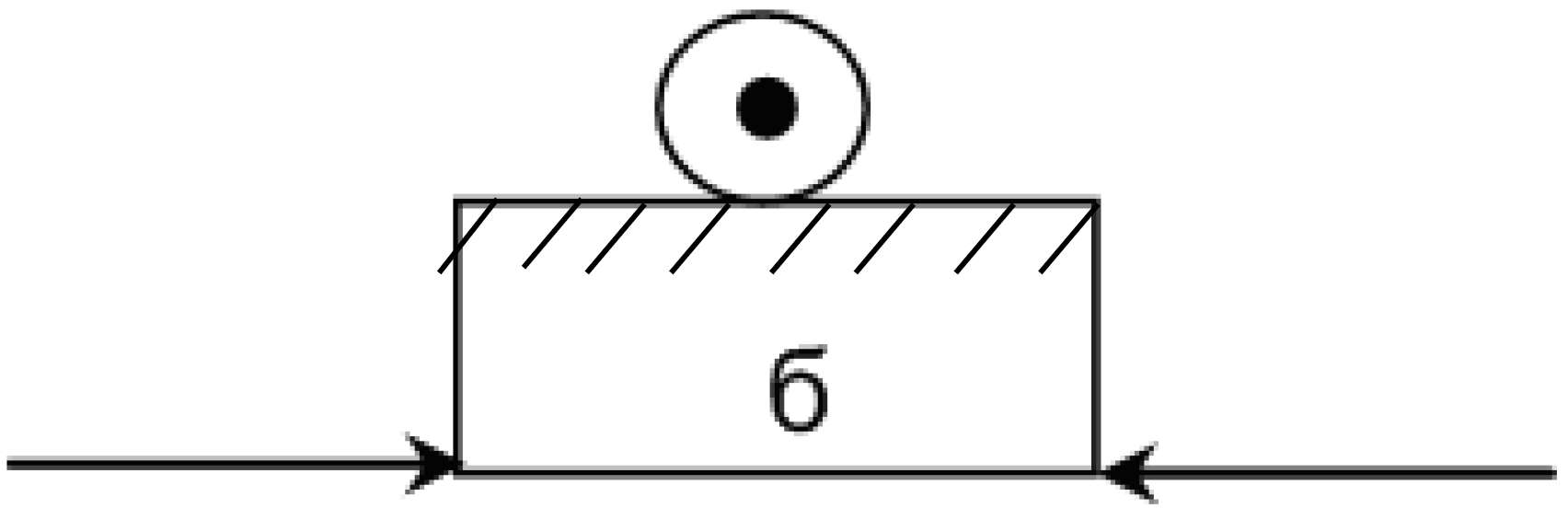
Потрібно розрізняти часові (а) та інерційні (б) запізнення. Для випадку (а) постійна часу ![]() , а
, а ![]() .
.
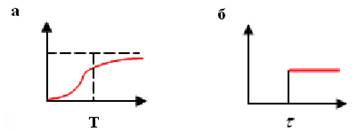
Рисунок 3.20 – Часові та інерційні запізнення
Згадаємо в яких реальних системах зустрічається запізнення.
1. Місяцехід.
За той час (≈ 2-3сек), доки зображення дороги дійде до пункту управління, і оператор подасть сигнал, місяцехід зміститься на ΔS ≈ 1м.
2. Бронтозавр.
Бронтозавр розпізнав, що його хтось вкусив за хвіст через 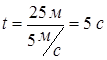 , і тільки через цей час − 5 секунд − зреагував.
, і тільки через цей час − 5 секунд − зреагував.
Чи не тому вони вимерли?
3. Підприємство, економіка.
На вході сировина, а на виході телевізор, автомобіль – із запізненням на 10-50 днів.
Розглянемо типову структурну схему САУ з запізненням. Може існувати два її варіанти.
1. Ланка запізнення в прямому колі.
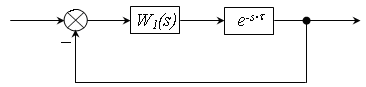
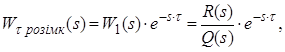
де ![]() – передаточна функція розімкненої САУ без урахування запізнення.
– передаточна функція розімкненої САУ без урахування запізнення.
2. Ланка запізнення в колі ЗЗ.
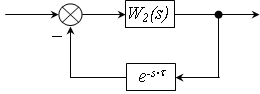
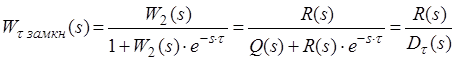 .
.
Видно, що незалежно від місця включення ланки, яка запізнюється, характеристичне рівняння системи із запізнення має вигляд
Це характеристичне рівняння має нескінченну множину коренів, оскільки
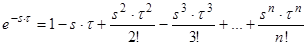 .
.
Для того, щоб ЛДС з постійним запізненням була стійкою, необхідно і достатньо, щоб усі корені рівняння (6) були лівими. Знаходження коренів рівняння (6) складне, тому для дослідження стійкості систем з запізненням використовують критерії стійкості. Найбільш зручно використовувати критерій Найквіста. Вперше цю задачу розв’язав радянський вчений Я.З. Ципкін.
Частотну передаточну функцію ![]() розімкненої системи з запізненням знаходять, підставляючи
розімкненої системи з запізненням знаходять, підставляючи ![]() в
в ![]() .
.
![]() .
.
З цього випливає, що АФЧХ САУ з запізненням відрізняється від АФЧХ цієї ж системи при ![]() тим, що для відповідної частоти зсув по фазі більше на
тим, що для відповідної частоти зсув по фазі більше на ![]() .
.
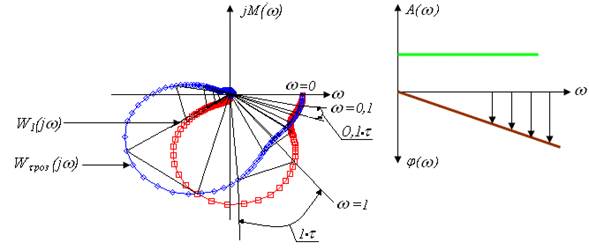
Рисунок 3.21 – Побудова АФЧХ з запізненням
3.11 Задача про граничне запізнення
Дано: деяка структура замкненої САУ з заданими передаточними функціями, яка містить в собі ланку запізнення.
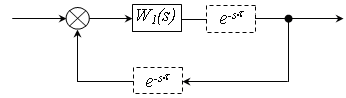
Знайти: ![]() . – граничне запізнення, при якому система знаходиться на межі стійкості.
. – граничне запізнення, при якому система знаходиться на межі стійкості.
Розв’язання:
Час запізнення ![]() . і відповідне йому значення частоти
. і відповідне йому значення частоти ![]() ., при яких
., при яких ![]() проходить через точку
проходить через точку ![]() , називають критичним.
, називають критичним.
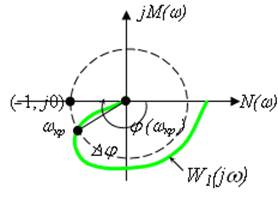
Рисунок 3.22 – Визначення граничного запізнення
![]()
![]()
− з цього виразу знаходимо ![]() .
.
![]()
З останнього виразу знаходимо ![]() :
:
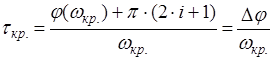 .
.
Визначати ![]() достатньо легко графічно.
достатньо легко графічно.
3.12 Оцінка якості регулювання САУ за часовими характеристиками
У стійкій системі перехідний процесс затухає. Однак, для практики не байдужий характер затухання перехідного процесу.
Так, наприклад, якщо перехідний процес затухає повільно, і система довго входить у новий режим, який встановлюється, то вона володіє недостатньою швидкодією, і, відповідно, її застосування буде обмеженим. Тому стійкість є необхідною, але не достатньою умовою працездатності САУ.
Достатньою умовою є якість процесів регулювання, яка оцінюється якістю перехідних процесів і помилками в режимах, які встановилися.
У різноманітті реальних вхідних сигналів оцінка якості САУ проводиться відносно стандартних вхідних сигналів (тест-сигналів).
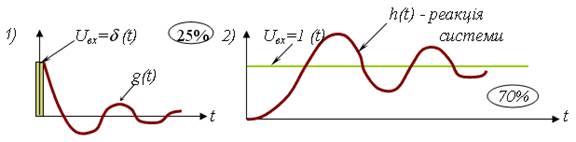
Рисунок 3.23 – Реакція системи на одиничний імпульсний та одиничний ступінчастий впливи
Такі види перехідних процесів складають ≈ 95%.
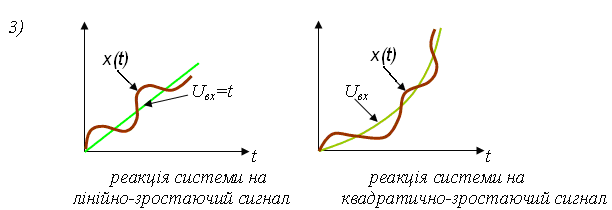
Рисунок 3.24 – Реакція системи на лінійно-зростаючий та квадратично-зростаючий сигнали
Частіше САУ оцінюється за одиничними скачками – 70%. Розглянемо реакцію системи на одиничний скачок.
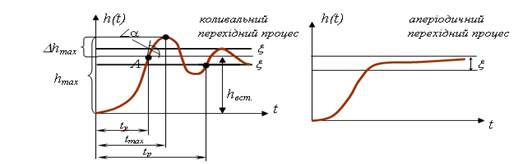
Рисунок 3.25 – Коливальний та аперіодичний перехідні процеси
Показники якості, які визначаються безпосередньо за кривою перехідного процесу, називають прямими оцінками якості.
Основні показники якості перехідного процесу:
- час регулювання ![]() ;
;
- перерегулювання ![]() ;
;
- власна частота коливань;
- кількість коливань;
- максимальна швидкість і максимальне прискорення величини, яка регулюється.
Час регулювання ![]() визначається тривалістю перехідного процесу. Теоретично перехідний процес триває нескінченно довго, але практично вважають, що він закінчується, як тільки відхилення регулюємої величини від нового його значення, яке встановилося, не будуть перевищувати допустимих меж
визначається тривалістю перехідного процесу. Теоретично перехідний процес триває нескінченно довго, але практично вважають, що він закінчується, як тільки відхилення регулюємої величини від нового його значення, яке встановилося, не будуть перевищувати допустимих меж ![]() . Звичайно приймають
. Звичайно приймають ![]() від
від ![]() .
.
Часом регулювання характеризують швидкодію системи. Однак, іноді швидкодію характеризують також часом ![]() досягнення перехідною функцією перший раз нового встановленого значення, або часом
досягнення перехідною функцією перший раз нового встановленого значення, або часом ![]() досягнення максимального значення
досягнення максимального значення ![]() .
.
Перерегулювання ![]() , або викидання, являє собою максимальне відхилення регулюємої величини від нового встановленого значення. Звичайно, перший максимум є найбільшим.
, або викидання, являє собою максимальне відхилення регулюємої величини від нового встановленого значення. Звичайно, перший максимум є найбільшим.
Відносне перерегулювання розраховують за формулою
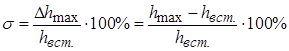
Час регулювання і перерегулювання – основні показники перехідного процесу, які тісно пов’язані між собою.
Перерегулювання з’являється внаслідок того, що система до необхідного встановленого стану підходить з певною швидкістю, яка графічно відображається тангенсом кута нахилу дотичної в точці А, що показано на рисунку вище. Чим більша ця швидкість, тим більше перерегулювання. Якщо зменшити перерегулювання, тобто швидкість, це призведе до збільшення часу регулювання.
3.12.1 Непрямі оцінки якості перехідних процесів
Всебічну оцінку якості перехідного процесу проводять за графіком перехідної функції, розрахунок і побудова якого є доволі важкими задачами.
У зв’язку з цим виникає питання: чи потрібно знати всі деталі перехідного процесу?
Непрямими оцінками називають деякі числа, які характеризують окремі сторони перехідного процесу. Перевага побічних оцінок в тому, що вони дозволяють в деякій мірі судити про вплив параметрів системи на її динамічні властивості.
Існує декілька непрямих оцінок якості перехідного процесу:
- оцінка по частотним характеристикам;
- інтегральні оцінки;
- кореневі методи і т.д.
Найбільш часто використовується інтегральна оцінка якості перехідного процесу. Найпростішою інтегральною оцінкою є
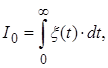
де ![]() – помилка системи,
– помилка системи,
![]() – дійсний стан системи;
– дійсний стан системи;
![]() – необхідний стан системи.
– необхідний стан системи.
Однак, ця оцінка може бути застосована тільки для перехідних процесів без перерегулювання, коли помилка не змінює свій знак.
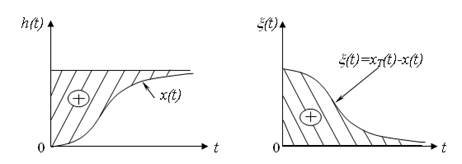
Рисунок 3.26 – Визначення помилки системи
Інтеграл визначає заштриховану площину, яку називають площиною регулювання.
При коливальному характері перехідного процесу застосовують інтегральну оцінку
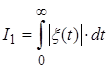
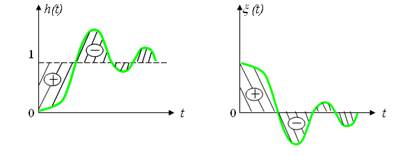
Рисунок 3.27 – Площина регулювання для інтегральної оцінки
Для оцінки як коливальних, так і монотонних перехідних процесів часто застосовується квадратична інтегральна оцінка, яка не залежить від знаку помилки, а значить і від характера кривої перехідного процесу.
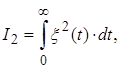
Заштриховану площину називають квадратичною площиною регулювання.
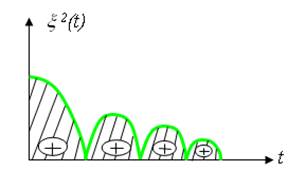
Рисунок 3.28 – Квадратична площина регулювання
Величина інтеграла ![]() тим менша, чим ближче перехідний процес до ідеальної ступінчатої зміни регулюємої величини. Інтегральна оцінка якості не завжди дає “кращий” ПП (перехідний процес).
тим менша, чим ближче перехідний процес до ідеальної ступінчатої зміни регулюємої величини. Інтегральна оцінка якості не завжди дає “кращий” ПП (перехідний процес).
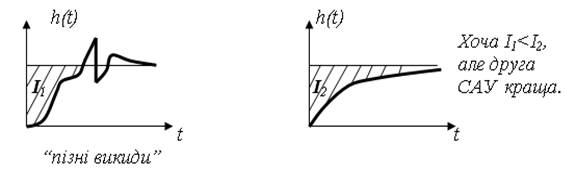
Рисунок 3.29 – Порівняння двох процесів за інегральною оцінкою
Не існує єдиновірного (який би підходив на всі випадки), критерія якості, крім марксизма-ленінізма.
3.12.2 Оцінка якості САУ в усталених режимах
У цьому розділі ми повинні отримати формули для визначення помилок у режимі, що встановився.
3.12.2.1 Передаточна функція по помилці
Дано:
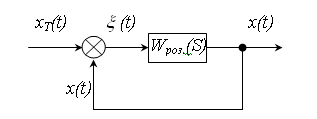
де ![]() – дійсний стан;
– дійсний стан; ![]() – необхідний стан системи;
– необхідний стан системи; ![]() – помилка.
– помилка.
Будемо розглядати слідкуючу систему, тобто ![]() .
.
Необхідно знайти: передаточну функцію по помилці.
![]()
Розв’язання:
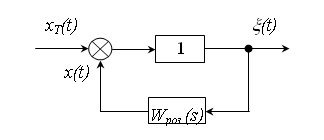
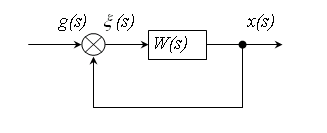
У підручниках дана задача розв'язується наступним чином (дивись структурну схему, подану при постановці задачі).
![]() .
.
Виконаємо перетворення Лапласа:
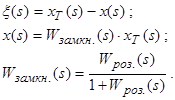
Тоді:
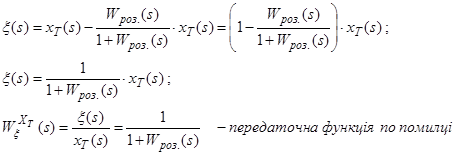
3.12.2.2 Усталені режими. Усталені помилки
ТАУ розглядає автоматичні системи в інформаційному плані, тобто з точки зору передавання і перетворення сигналів. Тому виникає запитання: з якою точністю передаються ці сигнали? Взагалі, нас буде цікавити точність відтворення впливу, який задається, а саме: з якою точністю виконується основна умова
![]() .
.
Помилка системи за впливом, який задається ![]() .
.
При існуванні перехідних процесів поточне значення помилки ![]() різко змінюється, і не може служити мірою точності автоматичних систем.
різко змінюється, і не може служити мірою точності автоматичних систем.
Тому, домовились точність САУ оцінювати величиною помилки, яка встановилася, що має місце в стійкій системі після завершення перехідного процесу.
Показником якості САУ в режимі, який встановився, вибирається величина похибки, яка встановилася:
![]() при
при ![]() .
.
(на практиці вказують ![]() в залежності від об’єкта).
в залежності від об’єкта).
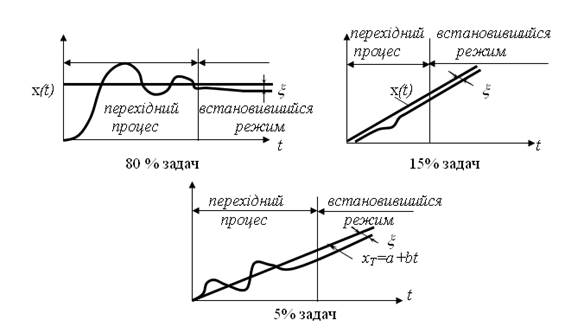
Рисунок 3.30 – Порівняльна оцінка застосування тестових вхідних сигналів
3.12.2.3 Отримання формул для помилок в усталених режимах
Дано: передаточна функція по помилці:
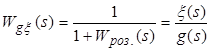
де ![]() – вхідний вплив.
– вхідний вплив.
Примітка:
для кратості та згідно з підручником Воронова прийнято ![]() .
.
Розв’язання:
Отримаємо з (3.25)
![]() .
.
Розкладемо ![]() в ряд за степенями
в ряд за степенями ![]() навколо точки
навколо точки![]() .
.
Навіщо ми це робимо: з властивостей перетворення Лапласа відомо, що значення виходу, яке встановилося, може бути отримане при s®¥ .
Отже,
Згідно визначення, коефіцієнти ряду Тейлора (коефіцієнти помилок) дорівнюють
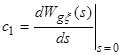 ;
;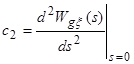 ;
; 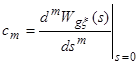 .
.
Виконаємо обернене перетворення Лапласа для ряду (7.7):
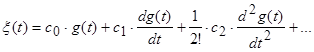
Отже, формули (3.27) для коефіцієнтів ![]() і ряд (3.28) дозволяють визначити вираз для помилки, яка встановилася, при будь-яких
і ряд (3.28) дозволяють визначити вираз для помилки, яка встановилася, при будь-яких ![]() .
.
1) Наприклад, нехай ![]() , тоді
, тоді ![]() , і
, і
![]() .
.
2) Нехай ![]() , тоді
, тоді ![]() , і
, і
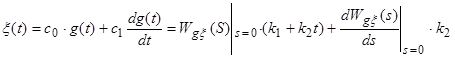 .
.
3.12.2.4 Астатизм
Коли говорять САУ володіє астатизмом 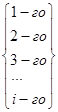 порядку?
порядку?
САУ з астатизмом першого порядку має значення
![]()
і, таким чином, при постійному впливі ![]() помилка, яка встановилася, дорівнює нулю.
помилка, яка встановилася, дорівнює нулю.
САУ з астатизмом другого порядку має значення
![]()
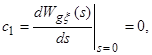
Помилка, яка встановилася у промисловому ргуляторі, буде дорівнювати нулю і при ![]() .
.
3.13 Промислові регулятори
Ця тема сьогодні має більше історичне значення. Раніше, до появи дешевих мікросхем, спеціалізованих і універсальних ЕОМ, важко було реалізувати складні закони управління. Для не дуже важких об’єктів управління були створені стандартні електронні блоки, які приймали сигнал помилки ![]() , підсилювали, перетворювали його і подавали на виконавчий елемент (нагрівач, електропривід тощо) управляючий сигнал. Можливі закони управління в цих промислових регуляторах обмежувались наступним набором:
, підсилювали, перетворювали його і подавали на виконавчий елемент (нагрівач, електропривід тощо) управляючий сигнал. Можливі закони управління в цих промислових регуляторах обмежувались наступним набором:
![]() – П-регулятор – пропорційний регулятор.
– П-регулятор – пропорційний регулятор.
![]() – ПД-регулятор – пропорційно-диференціюючий
– ПД-регулятор – пропорційно-диференціюючий
регулятор.
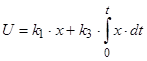 – ПІ – регулятор – пропорційно-інтегруючий
– ПІ – регулятор – пропорційно-інтегруючий
регулятор.
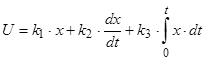 – ПІД – регулятор.
– ПІД – регулятор.
В останньому випадку вихідний сигнал пропорційний помилці і похідній від помилки, а також інтегралу від помилки. Інтеграл від помилки забезпечує астатизм САУ, похідна забезпечує демпфування – зменшення коливальності.
Контрольні питання:
- Наведіть побічні оцінки якості перехідного процессу.
- Що таке тест-сигнал?
- Яке значення має САУ з астатизмом першого порядку?
- Яке значення має САУ з астатизмом другого порядку?
- Дайте визначення перадаточній функції по помилці.
- Опишіть процедуру отримання формул для помилок в режимах, які встановилися
- Що таке показник якості САУ?