Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

4 СИНТЕЗ НЕПЕРЕРВНИХ САУ

4.1 Огляд і порівняльний аналіз методів синтезу

4.2 Класифікація критеріїв оптимізації САУ

4.3 Класифікація методів синтезу САУ

4.4 Синтез управління по вектору стану

4.5 Синтез управління по вектору стану при неповній його вимірюваності

4.6 Виведення властивостей САУ зі спостерігачем стану

4.7 Стійкість САУ із спостерігачем стану

4.1 Огляд і порівняльний аналіз методів синтезу

Визначення і постановка задачі синтезу САУ. Подамо специфікацію задачі синтезу.

Дано: математична модель об’єкта.

Вимоги до системи: – якість регулювання, тобто точність,

 – швидкодія,

 – інше.

Техніко-економічні характеристики: вага, енергоспоживання, надійність, вартість та інше.

Знайти: математичну модель регулятора, потрібні характеристики реалізуючи вимірювачів та виконавчих елементів (сенсорів та актуаторів) так, щоб задовольнити всі вимоги системи.

Під терміном “реалізуючий” мається на увазі пристрій, який можна виготовити або замовити. Подивимось на схему типової САУ: 

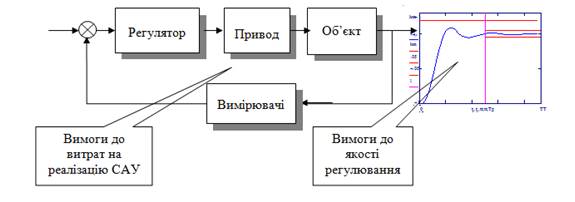
Задача синтезу – для заданого об’єкта визначити математичну модель (рівняння регулятора) та підібрати приводи та вимірювачі  так, щоб задовольнити вимогам до якості регулювання і витрат на реалізацію (вага, енергоспоживання, вартість системи, вартість експлуатації).

Сьогодні типова задача синтезу змінилася – характеристики приводів та вимірювачів відомі – вони просто вибираються з широкої гами високоякісних стандартних пристроїв. Не є проблемою реалізація регулятора – це теж стандартна плата з мікроконтролером та інтерфейсами. Треба тільки синтезувати алгоритм (закон) управління.  Програма, що реалізує алгоритм створюється автоматизованою системою проектування.

Але в типових задачах синтезу САУ характеристики об’єкта не є повністю відомими. Причина цього – усі “зручні” об’єкти вже автоматизовані, зостались не дуже “зручні”.  Як можемо бачити з цієї схеми, центром проектування сучасної САУ є саме синтез регулятора.

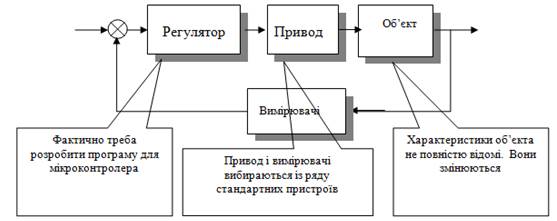
Рисунок 4.1 – Структурна схема САУ

Розглянемо ще один аспект синтезу САУ – оптимізацію. Деякі вимоги  задаються у виді обмежень: V < V_dopust,; V_j = 0. А деякі у вигляді: K® min або  K® mах.

Такі обмеження називаються критеріями, цільовими функціями – вони є функціями параметрів САУ. За рахунок вибору параметрів САУ необхідно мінімізувати (або максимізувати) ці критерії, при умові, що усі обмеження задовольняються.

Зауваження. Там, де це узгоджено із здоровим глуздом, можнавикористовувати нечіткі обмеження – це полегшує розв’язання оптимізаційної задачі. Наприклад, для підсистеми стабілізації висоти головки зчитування з компакт диска обмеження  0 < h – (висота головки над диском) – повинно бути дуже чітким, бо при 0 £ h можливе торкання головки до диску з пошкодженням поверхні диску. Для підсистеми позиціонування головки над заданим треком обмеження - dop < Dd < dop можна зробити нечітким – при його незначному порушенні просто погіршиться якість зчитування, але катастрофи не буде.

Оптимізаційні задачі синтезу та оптимальні САУ ми будем розглядати детально у другій частині курсу.

Підведемо підсумки розгляду задачі синтезу і подамо її стисле формулювання.

Дано:

1) об’єкт + вимірювачі + виконавчі пристрої = незмінна частина САУ (диф. рівняння, передаточні функції)

2) вимоги: – обмеження;

                   – критерії і цілі оптимізації.

Потрібно: отримати алгоритм або рівняння, або передаточну функцію регулятора, що може бути реалізований доступними технічними засобами  і задовольняє усім вимогам.

4.2 Класифікація критеріїв оптимізації САУ

Термін критерій настільки широко вживається, що фактично втратив смисл (сенс). Ми визначаємо критерій як числову міру для визначення відношення переваги  або ранжування альтернативних варіантів САУ.

Слід пам’ятати одне важливе обмеження критеріальних мір. Розглянемо його на прикладі: для САУ1 критерій  =К₁ = 10, для САУ2, відповідно К₂ = 20, ціль оптимізації К® max. Можна стверджувати, що САУ2 краще САУ1, але в загальному випадку не можна говорити, що САУ2 вдвічі краща САУ1 ().

Критерій є функцією або функціоналом від параметрів САУ. В цьому аспекті критерії поділяють на локальні  та інтегральні:

Локальний критерій: G(X(t_k)) – функція координати об’єкта управління взятої в певний момент часу. Наприклад, помилка влучання (попадання) для ракети.

Інтегральний критерій:  – інтеграл (або сума для дискретних систем) від координати об’єкта. Наприклад, усім відома інтегральна квадратична помилка в перехідному процесі.

Розглянемо типові  критерії, що використовуються для синтезу САУ.

Локальні критерії (за традицією їх позначають G₀ ).

Тривалість перехідного процеса:

G1₀ = Т_р.

Викид (максимальне перерегулювання):

G2₀ =  max(X(t) - X_задане) = h_m.

Усталена помилка (після закінчення перехідного процесу):  

G3₀ =  (X(Т_р) - X_задане).

Максимальне прискорення:

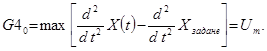
Цей критерій застосовується для САУ об’єктами, що не допускають великих навантажень.

Розглянемо інтегральні критерії.

Інтегральна квадратична похибка дуже часто використовується в наукових працях і підручниках. Головна причина такої популярності в тому, що похідна від підінтегрального виразу – лінійна функція змінної, що регулюється.

Більш реалістичним є критерій – інтеграл від зваженого модуля помилки. Але він не дає аналітичних розв’язань оптимізаційних задач. Запишемо вирази для цих критеріїв.

.

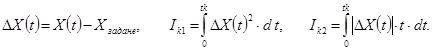Щоб зрозуміти різницю між критеріями, побудуємо типові графіки для підінтегральних виразів:

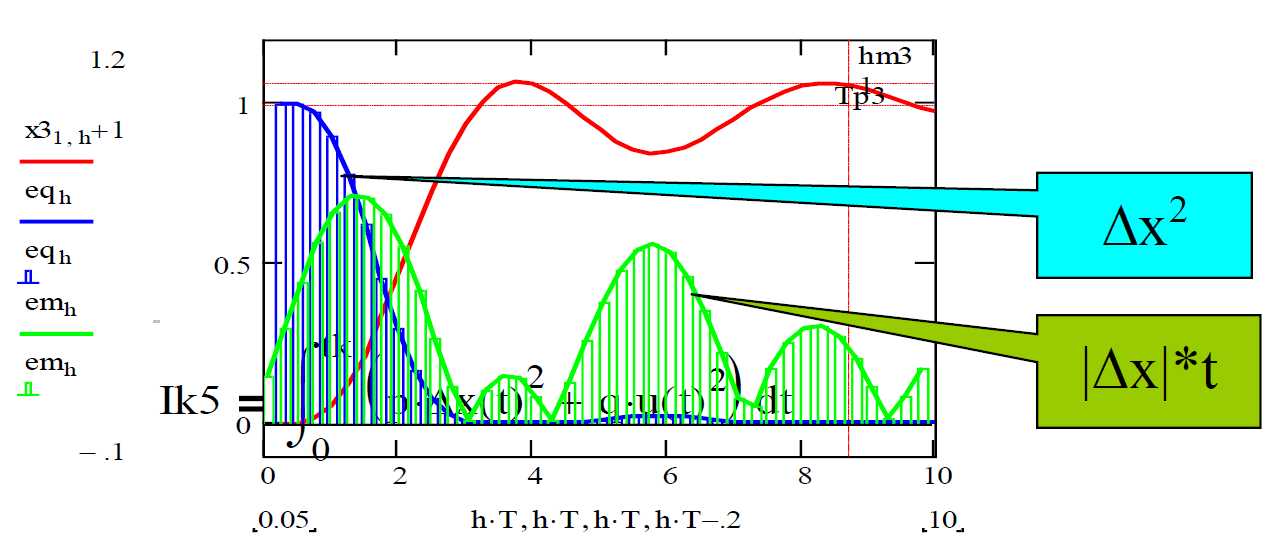
Рисунок 4.2 – Типові графіки для підінтегральних виразів

Як видно з графіка, в критерії зваженого модуля помилки (англійський термін для таких критеріїв – “функція штрафу”) більша вага дається пізнім помилкам – саме такі помилки є небажаними для САУ. Бачимо також, що процес задовільний по одному критерію є незадовільним по іншому.

На практиці також використовуються такі інтегральні критерії:

;  

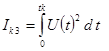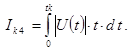
Критерій I_k3 є оцінкою енергії витраченої на управління. Розглянемо електродвигун як виконавчий елемент. Потужність його буде

,

де U – напруга,

R_я – опір обмотки якоря.

Тобто, якщо U є управлінням, то критерій  I_k3 – інтеграл від потужності є роботою витраченою на управління.

Критерій Ik₄ є оцінкою розходу робочого тіла витраченого на управління.

Часто використовують узагальнений квадратичний критерій – суму критеріїв з відповідними ваговими коефіцієнтами. Широко використовується такий узагальнений інтегральний критерій оптимальності САУ:

.

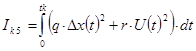де q і r – вагові коефіцієнти, що вибираються “експертними методами”,тобто чисто суб’єктивно.

4.3 Класифікація методів синтезу САУ

Методи синтезу САУ залежать від того:

1) яку структуру закону управління ми задаємо – лінійний / нелінійний,

неперервний / дискретний / релейний, які вхідні дані ми використовуємо для управління – тільки те, що безпосередньо вимірюється, чи абстрактний вектор стану.

2) для якого об’єкту синтезується САУ – лінійного/нелінійного, неперервного/дискретного, стаціонарного/нестаціонарного.  

Методи оптимізації класифікуються на:

– приблизні і точні;

– аналітичні і пошукові.

Для неперервних лінійних систем управління найбільш відомі  такі методи синтезу:

1. Метод логарифмічних амплітудно-частотних характеристик.
2. Метод кореневих годографів.
3. Управління по вектору стану. Метод стандартних коефіцієнтів.
4. Оптимізаційні методи синтезу.
5. Пошукові методи синтезу.

Проаналізуємо недоліки і переваги цих методів.

Розглянемо метод логарифмічних амплітудно-частотних характеристик

Приблизний, майже не потребує складних обчислень. Ідея методу – знайти логарифмічну частотну характеристику (ЛАЧХ) регулятора як різницю між бажаною ЛАЧХ і ЛАЧХ незмінної частини САУ. Бажана ЛАЧХ будується так, щоб частота зрізу відповідала потрібній швидкодії, а ділянка характеристики навколо частоти зрізу мала нахил і довжину 1-2 декади. Метод був дуже поширений в СРСР – „Простий метод для простих систем”.

Розглянемо метод кореневих годографів.

Графоаналітичний метод. Дозволяє вести як приблизні, так і точні розрахунки перехідних процесів та їх характеристик. Ідея методу – побудова траєкторій коренів характеристичного рівняння (годографів) в функції вибраного параметру (звичайно – загального коефіцієнта підсилення k_o). Тоді для певного значення параметру на годографі можна побачити розташування коренів замкненої системи. Спеціаліст одразу за коренями може оцінити показники якості перехідного процесу. Точний розрахунок перехідного процесу виконувався графо-аналітично за допомогою спеціальної логарифмічної лінійки. Побудова самого кореневого годографа (як і побудова ЛАЧХ) може виконуватись практично без обчислень. Метод був дуже поширений в США – „Простий метод для складних систем”. 

Розглянемо метод стандартних коефіцієнтів.

Починаючи з 1970 року – базовий метод синтезу у всьому світі. Прийшов цей метод одночасно з поширенням комп’ютерів – засобів синтезу  та аналізу, і мікроконтролерів – засобів реалізації регуляторів. Точний метод синтезу і розрахунку параметрів регуляторів. Для аналізу і синтезу диференціальне рівняння замкненої САУ приводиться до форми Коші (системи із N-диф. рівнянь першого порядку, де N – порядок системи). Набір змінних форми Коші – вектор стану – Х= (х₁, х₂,... , х_N). 

Ідея методу – перехідний процес однозначно визначається коренями характеристичного рівняння замкненої системи, а корені  однознач визначаються коефіцієнтами характеристичного  рівняння. При управлінні по вектору стану   можна дати усім коефіцієнтам потрібні значення. Потрібні значення коефіцієнтів характеристичного рівняння (стандартні коефіцієнти) знаходяться раз і назавжди і подаються в спеціальних таблицях. Існують різні набори стандартних коефіцієнтів – для систем оптимальних за швидкодією, розходом енергії, перерегулюванням та іншим.

Єдина проблема – знайти ці коефіцієнти, для цього використовують методи варіаційного числення, динамічного програмування та ін.  Головний недолік методу –  звичайно неможливо виміряти усі складові вектору стану – тому використовують спостерігачі.

„Складний, орієнтований на ЦОМ, метод для складних систем”.

Розглянемо оптимізаційні методи синтезу.

Задача синтезу САУ (знайти функцію управління у вигляді u(t), або u(x) – це управління  в програмній і координатній формі відповідно) є варіаційною задачею. Для синтезу оптимального управління використовуються класичне варіаційне числення, метод принципу максимуму, метод динамічного програмування та ін. Ідея варіаційного числення  – знаходження функції, що дає екстремум функціоналу (функції від функції). Це розширення ідеї знаходження екстремуму звичайної функції (похідна функції рівна нулю ® варіація функціоналу рівна нулю). Зростання обчислювальної потужності МП та МК дозволило навіть вбудовувати ці складні методи в мікроконтролери. Оптимальне управління знаходиться в реальному часі згідно поточним значенням параметрів об’єкта і поставленим задачам. Так, зокрема, працюють системи термінального управління.

Розглянемо пошукові методи синтезу.

Суть цієї групи методів в тому, що параметри регулятора знаходяться методом послідовних наближень, методом випадкового пошуку. Фактично над звичайною САУ ставлять ще одну САУ, задача якої так регулювати параметри першої, щоб залишались постійними критерії якості. Це так звані САУ з самонастроюванням. Сьогодні це не просто популярний, а навіть занадто популярний науковий напрямок. Сюди відносяться так звані методи „колективної поведінки” – „торги”, „аукціони”, „методи відкритого управління” – це методи з солідним теоретичним і практичним базисом, також методи „нечіткої логіки”, „нейронних мереж”, „генетичних алгоритмів”, де інформаційного шуму  більше, ніж результатів. Теорія управління взяла ці методи з біології та економіки, де вони є природними і працюють стихійно. На жаль, поведінка таких систем занадто складна і непередбачувана (згадаємо випадки патологічної поведінки живих істот, популяцій, біржові паніки). Але це один з головних напрямків розвитку науки. Існує ще багато інших методів, наприклад – метод фазової площини – переважно для релейних САУ, метод зворотних частотних характеристик, ін.

Сьогодні задача синтезу переноситься в мікроконтролер і там періодично, певними методами виконується на базі поточної ідентифікації параметрів об’єкта управління. Проектувальник повинен вибрати критерії, структуру і загальну логіку поведінки системи управління.

4.4 Синтез управління по вектору стану

Будемо розглядати задачу синтезу на прикладі типової системи 3-го порядку:

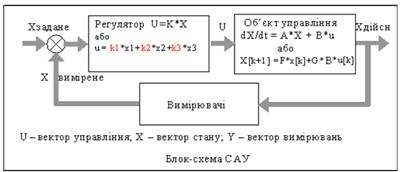
Рисунок 4.3 – Приклад типової системи 3-го порядку

Далі буде досить довге обґрунтування і викладення методу. Тому, подамо стисло послідовність кроків синтезу регулятора для нашого прикладу:

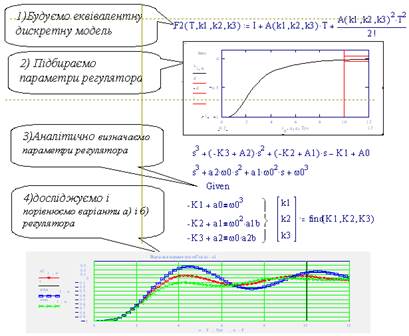
Рисунок 4.4 – Послідовність кроків синтезу регулятора для нашого прикладу

З цієї послідовності власне до синтезу відноситься пункт 3.

Спочатку слід записали еталонне характеристичне рівняння, що дає бажаний перехідний процес. Далі записати характеристичне рівняння замкненої САУ в загальному вигляді.

Прирівняли вирази для коефіцієнтів характеристичного рівняння  потрібним для них значенням. Отримали систему рівнянь для визначення параметрів регулятора k₁, k₂, k₃. Оце і весь синтез. А тепер розглянемо це детальніше.

Пригадаємо, що однорідне диференціальне рівняння n-ого степеня:

має розв’язання:    

.

де s₁, s₂, s_n – корені характеристичного рівняння ;

С₁, С₂, С_n – постійні, що визначаються з граничних умов.

Перехідний процес однозначно визначається коренями характеристичного рівняння. Із курсу алгебри відомо, що коефіцієнти алгебраїчного рівняння однозначно визначаються коренями цього рівняння. Тому, можна стверджувати, що коефіцієнти характеристичного рівняння визначають перехідний процес. На цьому базується ідея методу стандартних коефіцієнтів.

Відібрати перехідні процеси оптимальні по різним критеріям, для цих перехідних процесів визначити коефіцієнти характеристичних рівнянь замкненої (керованої) системи, що відповідають цим перехідним процесам, створити таблиці стандартних коефіцієнтів для систем різних порядків – 2, 3, 5, 6, 7-го.

Процес синтезу буде складатись з таких кроків:

• виходячи з вимог до системи, вибрати еталонний перехідний процес (ПП);
• взяти стандартні коефіцієнти, що відповідають цьому ПП;
• виходячи з потрібної швидкодії, обчислити потрібні значення кое-фіцієнтів характеристичного рівняння;
• обчислити параметри регулятора, що забезпечують ці значення коефіцієнтів характеристичного рівняння

Розглянемо задачу синтезу методом стандартних коефіцієнтів (СК) згідно цієї послідовності і форми Вишнєградського для диференціального рівняння.

Множину потрібних еталонних процесів можна скоротити, якщо збирати до одного класу процеси, що відрізняються тільки масштабом часу. Усі такі процеси певним перетворенням можна звести до одного й того ж еталонного процесу у безрозмірному часі. Це робиться так, як наведено нижче.

Дано диференціальне рівняння САУ в нормованому відносно складової з вищою похідною виді (для прикладу беремо 4-го степеня):

.

Введемо параметр “власна частота”:

.

Введемо нові – безрозмірні коефіцієнти:

.

Визначимо через них розмірні коефіцієнти: 

.

Підставимо їх у диф. рівняння:

.

Введемо безрозмірний час і замінимо розмірні похідні безрозмірними:

Підставимо їх у диф. рівняння:

.

Отримуємо диф. рівняння у безрозмірному часі.

.

Це і є форма Вишнєградського для подання диференційного рівняння. Її особливість – перший і останній коефіцієнти  дорівнюють  “1”.

Вишнєградський отримав цю форму займаючись (більше 100 років тому) задачею синтезу регулятора. Крім цього Вишнєградський був (недовго) міністром фінансів (успішним) і біржовим гравцем (не дуже, чому й прийшлось піти з посади міністра).

Графіки такого сімейства процесів мають вигляд:

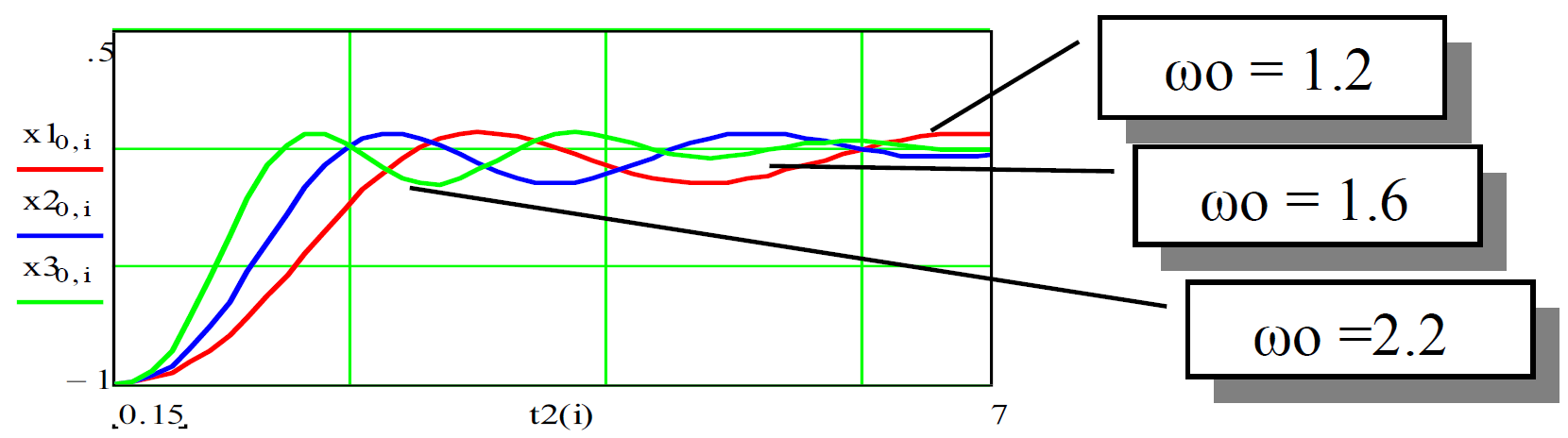
Рисунок 4.5 – Сімейство перехідних процесів при різних w₀

Розглянемо приклад еталонних процесів і відповідні стандартні коефіцієнти.

На цьому графіку подано перехідні процеси (для систем 2, 3, 4, 5, 6 порядків) і стандартні коефіцієнти для випадку кратного розподілення коренів – без перерегулювання.

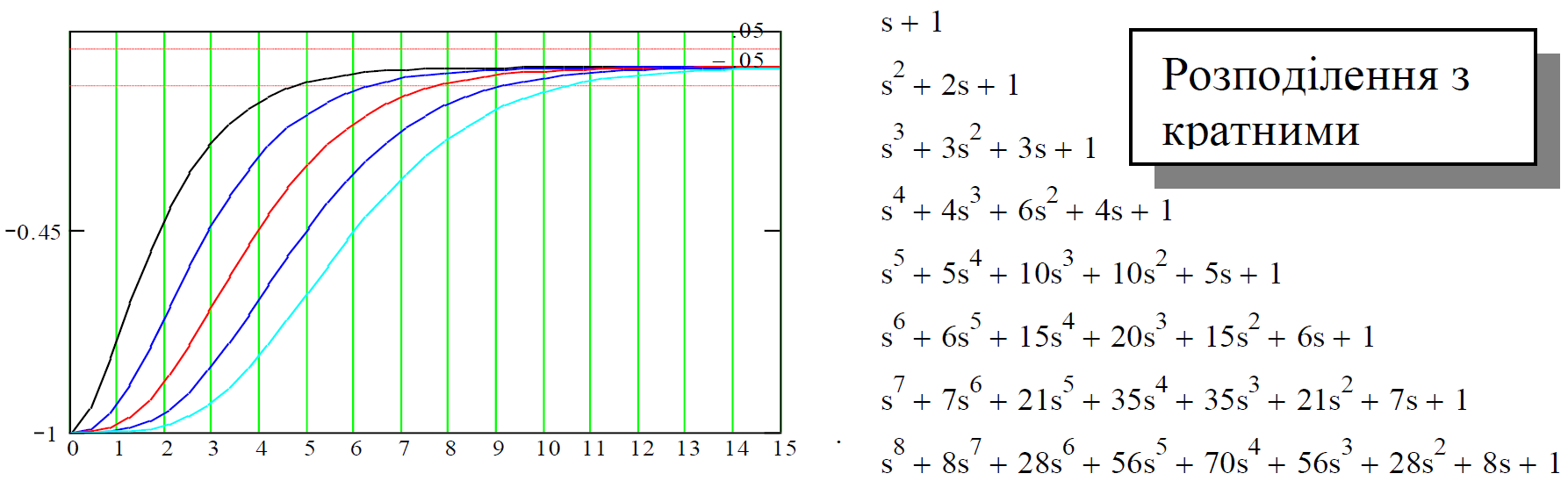
Рисунок 4.6 – Перехідні процеси і стандартні коефіцієнти

Усі корені дійсні і однакові:

s_і = -1,  і = 1 … n.

Такі процеси вибирають для випадків, коли потрібний викид h_m = 0 і бажано мінімізувати навантаження на об’єкт.  Недолік процесів з кратними коренями – відносно високі тривалості перехідних процесів (ПП). Використовуються також інші еталонні процеси.

Порядок розв’язання задачі синтезу управління по вектору стану.

Ми розглянули загальну постановку задачі синтезу, оптимальності, еталонні ПП. Тепер можемо подати задачу синтезу у вигляді певної послідовності кроків, можна сказати, – алгоритму синтезу.

,

де, наприклад:

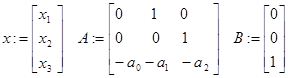
1. Дано:

а) дифрівняння системи у канонічній формі Коші;

б) вимоги до якості регулювання: 

2. Управління шукаємо у вигляді: ,

де К – матриця (вектор для одноканального управління)

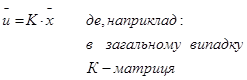
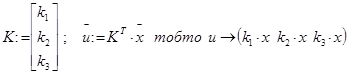
3. Знайти. Задача синтезу зводиться до знаходження усіх елементів К, таких, що САУ задовольняє поставленим вимогам – К ?

Тепер запишемо, власне, послідовність кроків синтезу:

1. Підставляємо вираз для управління в диф. рівняння об’єкта:

.

2. Виконуємо перетворення Лапласа для цього рівняння і маємо:

 .

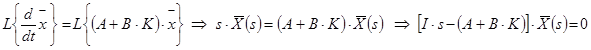Дивимось на останнє рівняння і бачимо, що:

а) – це дає так зване тривіальне розв’язання  х(t) º 0 і нас не цікавить;

б)  – це дає нам рівняння для визначення К.

Детермінант від цього матрично-векторного  виразу дає нам систему лінійних однорідних алгебраїчних рівнянь. Як відомо з курсу алгебри, ця система має нетривіальне розв’язання тільки якщо детермінант матриці коефіцієнтів дорівнює нулю (можна це трактувати так – коли перенесемо якусь змінну у праву частину – формально отримаємо систему з n рівнянь для (n-1)змінних. Щоб така система мала несуперечливе розв’язання, одне рівняння повинно бути “зайвим” – лінійною комбінацією інших. Відомо, що детермінант такої системи дорівнює нулю. 

3. Розкриваємо детермінант і отримуємо характеристичне рівняння замкненої САУ.  Для системи 3-го порядку:

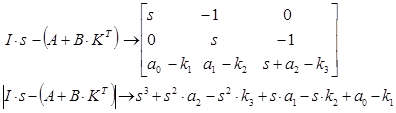
Збираємо коефіцієнти при однакових степенях і отримуємо характеристичне рівняння замкненої САУ, коефіцієнти якого А_і залежать від параметрів об’єкта  та невідомих поки параметрів регулятора:

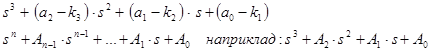
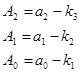
4. Вибираємо еталонний ПП, беремо (з таблиці, або документа) значення стандартних коефіцієнтів, безрозмірної тривалості ПП, викиду.

5. Обчислюємо потрібну власну частоту і потім, згідно залежності записуємо вирази для потрібних значень коефіцієнтів:

.

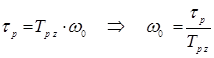6. Прирівнюємо коефіцієнти при однакових степенях у характеристичному рівнянні замкненої САУ і “безрозмірному” еталонному характеристичному рівнянні. Так отримуємо систему рівнянь для визначення невідомих параметрів регулятора:

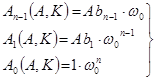
Для прикладу – системи 3-го порядку  це розв’язання майже очевидне:

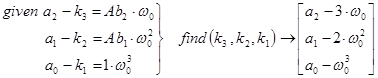
Задача синтезу регулятора по вектору стану має одну й ту ж структуру для лінійних динамічних систем довільного степеню. Задача зводиться до розв’язання системи алгебраїчних (звичайно нелінійних) рівнянь.

4.5 Синтез управління по вектору стану при неповній його вимірюваності

Спостерігач (інші назви: динамічний компенсатор, асимптотичний ідентифікатор та ін.) використовує безпосередньо вимірювані компоненти Y вектора стану Х та вектор управління  u і дає оцінку  Х_n  усього вектора стану (але може оцінювати тільки окремі компоненти вектору стану).

Розглянемо структурну схему САУ зі спостерігачем. Як же все таки (у 1950-70 роки) прогресивне людство прийшло до ідеї спостерігача? Далі подано три структурних схеми – три кроки до остаточної робочої схеми.

 На цих схемах: Х – вектор стану; X_n – оцінка вектора стану; Y – вектор вимірювань; U – вектор управління. 

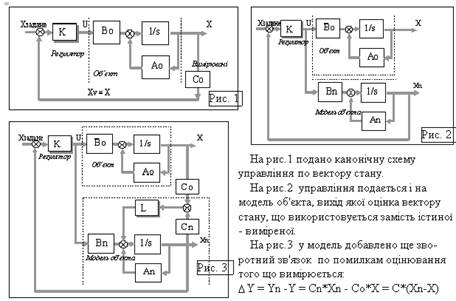
Рисунок 4.7 – Структурна схема САУ зі спостерігачем

Розглянемо стисло історію та логіку цих трьох кроків.

Перший крок (1940-1950 р.р.). САУ приводиться до стандартного, незалежного від розмірності матрично-векторного виду:  ;  задається вид управління:  по вектору стану.

Синтез управліннят(визначення К) стандартизується, як і сама САУ, її легко реалізувати на базі ЦОМ.

Проблема – тільки деякі компоненти вектору стану (математичної абстракції) звичайно вимірюються. Як отримати повний вектор стану?

Другий крок (1950-1960 р.р.). Інтенсивно використовуються аналогові засоби моделювання динамічних систем. Якщо зробити ТОЧНУ модель динаміки об'єкта і подавати на цю модель теж саме управління, що і на об'єкт, то вихід моделі, де ми усе можемо вимірювати, необхідний нам вектор стану.

Проблема – на модель треба подавати і збурення, а вони звичайно не вимірюються, модель повинна бути абсолютно точною. Інакше вихід моделі постійно буде розходитись з виходом об'єкта.

Третій крок (1960-1970 р.р.). ЦОМ за масою і габаритами ще поступається аналоговим ОМ, але починається ера мікропроцесорів. Ідею моделі об'єкта, як засобу оцінки вектору стану, можна зробити придатною для практики, якщо ввести зворотний зв'язок – "штраф" – L за відхилення оцінки того, що вимірюється, від того, що реально виміряно.

Проблема №1 – модель об'єкта повинна бути досить точною – частково розв'язується ідентифікацією параметрів моделі (це теж може виконати спостерігач).

Проблема №2 – спостерігача придумала не одна людина. Над цим працювало багато вчених. Але першим виклав це у зручному для інженерів виді американський вчений Люенбергер у роботі "Введення в теорію спостерігачів". Він і ввів термін "observer". У теорії спостерігачів є паралельний науковий напрямок – фільтри Вінера-Калмана.

Фільтр Калмана структурно ідентичний спостерігачу. Це теж модель об'екта із зворотним зв'язком по помилці виміряного вектору стану і його помилки. Фільтр вводиться у тих випадках, коли вектор стану вимірюється з випадковими помилками (шумами). Для управління використовується оцінка вектору стану. Ця оцінка коректується пропорційно "помилці" оцінювання, але коефіціент "штрафу" K (замість L) тим менше, чим більше рівень шумів. 

Постановка задачі синтезу САУ зі спостерігачем стану

Запишемо канонічне означення в задачі синтезу САУ із спостерігачем, вектору стану.

Дано:

об'єкт  та  вимірювачі    

cпостерігач  = модель об'єкта .

та модель вимірювачів  ;

регулятор  .

Зверніть увагу – для управління використовується оцінка вектору стану. Вимоги до якості регулювання задаються як вимоги до параметрів перехідних процесів (ПП) у основному контурі і контурі спостерігача, наприклад: T_pp, h_mp, T_pn, h_mn – тривалості ПП і викиди для цих контурів відповідно. Звичайно тривалість ПП у спостерігача повинна бути

T_pn = (0.1 - 0.25)·T_pp.

На другому етапі вибираються або знаходяться, як розв'язання оптимізаційної задачі, потрібні значення коефіцієнтів характеристичних рівнянь контуру регулятора і спостерігача. Потім коефіцієнти характеристичних рівнянь  контуру регулятора і спостерігача прирівнюються до їх потрібних значень – так отримуємо по N рівнянь для кожного контуру, до цих  рівнянь додаються інші умови – так отримуємо систему нелінійних рівнянь, з яких знаходимо параметри регулятора – матрицю К та параметри спостерігача – матрицю L. Перекладемо слова на мову математики. 

             .

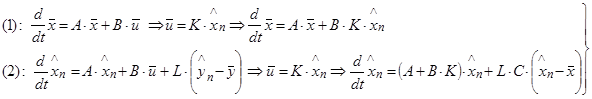
Для синтезу і аналізу стійкості нам потрібні характеристичні рівняння САУ без спостерігача і спостерігача, як слідкуючої системи. Нагадаємо процедуру: беремо відповідну однорідну (зовнішні входи рівні нулю) систему диф. рівнянь і виконуємо перетворення Лапласа. Потім, виходячи з умови отримання нетривіальних розв'язків прирівнюємо детермінант відповідної матриці до нуля. Розкриваємо його і отримуємо алгебраїчне рівняння степеню N відносно змінної s.

Навіщо воно нам? Якщо всі параметри САУ відомі, ми зможемо знайти корені цього рівняння – визначити стійкість САУ, побудувати  перехідний процес.

При синтезі, навпаки, задаємо значення коефіцієнтів, що забезпечують потрібний ПП і знаходимо параметри регулятора. 

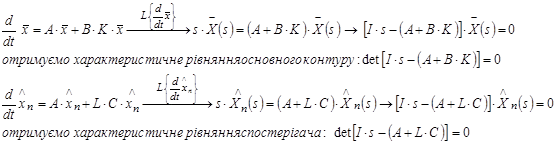
Зауваження. З рівняння спостерігача виключено складові  та  –  для контуру спостерігача це зовнішні входи, а стійкість ми визначаємо для власного руху.

.

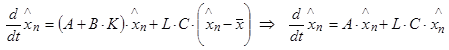4.6 Виведення властивостей САУ зі спостерігачем стану

Замість змінних  – координата та  – її оцінка спостерігачем, введемо змінну  – помилка оцінювання. Виконаємо алгебраїчні перетворення:

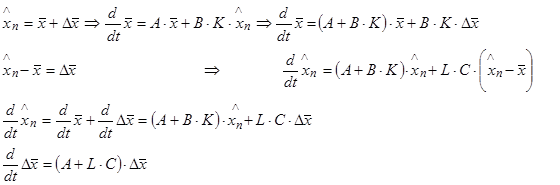
Зрозуміло все, але прокоментуємо.

Виключили X_n з (1) – отримали (5); виключили з (2) – отримали (6). З рівняння (6) відняли (5) – отримали (7). Тепер об'єднаємо рівняння (5) і (7) в одне матрично-векторне диф. рівняння.

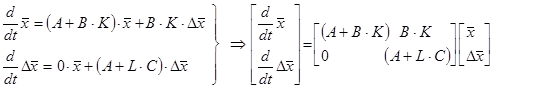
Отримали таку систему дифрівнянь порядку 2•N. (0 – це матриця з          нулів)

.

Проаналізуємо її. Запишемо характеристичне рівняння системи:

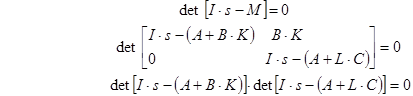
Бачимо, що характеристичне рівняння розпадається (згідно з властивостями блочних матриць) на два окремих рівняння, одне з яких характеристичне рівняння САУ без спостерігача, друге – характеристичне  рівняння спостерігача. Це означає, що параметри  регулятора К та параметри спостерігача L  можна розраховувати незалежно.

4.7 Стійкість САУ із спостерігачем стану

Чи можна зробити спостерігача стійким? Бачимо, що корені спостерігача визначаються  характеристичним рівнянням:

.

В це рівняння входить матриця параметрів спостерігача L. При умові спостерігальності вибором L можна зробити спостерігача стійким.

Властивості спостерігача стану

Отримані результати є фактичним доказом таких властивостей спостерігача стану:

1) в усталеному стані помилка оцінювання  дорівнює нулю (прирівнюємо похідну до нуля і бачимо  повинно бути рівним нулю).

2) спостерігач стану не змінює корені основного контуру, а тільки додає свої.

3) задачу синтезу САУ із спостерігачем можна розділити на дві незалежні – синтез основного контуру і синтез контуру спостерігача.

Розглянемо поняття керувальності та спостерігальності були введені Калманом. Ці поняття важливі для аналізу багатомірних систем високого порядку.

Неформально ситуації а) керувальності та б) спостерігальності можна визначити так, розглядається багатомірна система:

а) в системі немає ізольованих підсистем, куди не досягає дія управління (для цього вектор управління повинен мати певну розмірність, матриця В – не дуже багато нулів);

б) в системі немає ізольованих підсистем, в яких не встановлено хоч один вимірювач, тобто немає інформаційно ізольованих підсистем.

Формально це визначається так:

Керувальність (,,управляемость”): ранг прямокутної матриці, що складена з таких матриць повинен бути рівним N-порядку системи.

Спостерігальність (,,наблюдаемость”): ранг прямокутної матриці, що складена з таких матриць повинен бути рівним N.

Контрольні питання:

1. Наведіть властивості спостерігача стану.
2. Що таке керувальність та спостерігальність?
3. Чому відповідні параметри спостерігача Люенбергера і фільтра Калмана мають означення K та L?
4. Наведіть канонічну схему управління по вектору стану.
5. Дайте характеристику фільтру Калмана.
6. Що таке форма Вишнерадського?
7. Наведіть постановку задачі синтезу.