Т. М. Боровська. Теорія автоматичного управління. Курс лекцій

До імпульсних систем відноситься в частковості вся САУ з ЦОМ. В імпульсних САУ де-які параметри змінюються скачками. Чи потрібні імпульсні САУ, може це САУ 2-го сорту в порівнянні з безперервними? Які САУ багатші по можливостям - імпульсні чи безперервні?

Приклади імпульсних САУ:

1) Система управління потужним електроприводом (тірісторами, напівпровідниками).

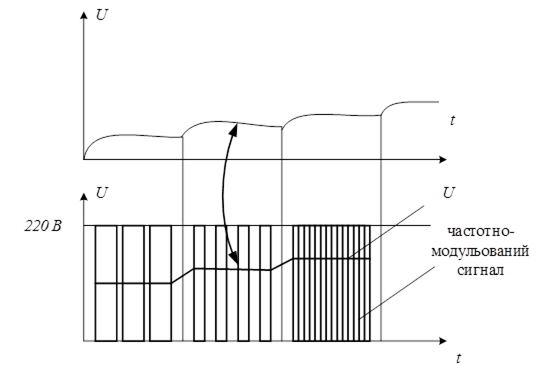
Рисунок 5.1 – Частотно-імпульсна модуляція в системі управління електроприводом

Для напівпровідникових елементів вигідна робота в режимі насичення, фактично в режимі "включено-виключено". Втрати в цьому випадку мінімальні. Тому системні регулювання потужних електроприводів роблять імпульсними.

2) САУ з ЦОМ.

ЦОМ - імпульсний елемент в силу принципів функціонування. Вхідні сигнали сприймаються, а вихідні видаються дискретно, хотя частота квантування по часу може бути дуже великою. В ЦОМ сигнали квантовані не тільки по часу, але й по рівню. Оскільки розрядність дискретного представлення чисел в ЕОМ як правило велика, то в більшості прикладних задач квантуванням по рівню нехтують. Однак, це не завжди допустимо (накопичення похибок округлення).

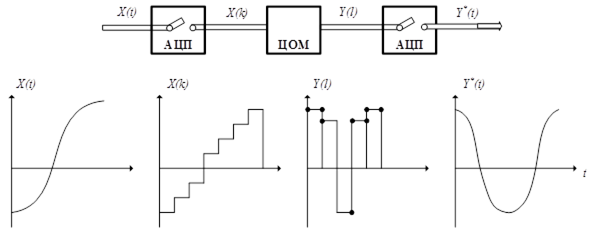
Рисунок 5.2 – ЕОМ як елемент САУ

На рис. 5.2 позначено: к- номер кроку квантування вхідного сигналу; l- номер кроку квантування вихідного сигналу. Слід відзначити що параметри квантування по рівню і по часу для входу і виходу ЦОМ не обов'язково повинні бути однаковими.

3) Радіолокаційні лазерні системи (для них також є звичайним режим "посилання - отримання" імпульсів)

4) Органи зору роботів

Навіть зорова система людини працює в імпульсному режимі сканування. Якщо приклеїти мікродзеркало на око, то можливо зафіксувати стрибки.

5) Цифровий запис звуку і зображень та їх послідовна обробка - фільтрація, кодування.

{Подивіться в літературі опис названих вище та інших імпульсних систем.}

5.2 Класифікація ІСАУ

Процес перетворення неперервних сигналів в дискретні або квантовані сигнали називають квантуванням.

Розрізняють 3 способи квантування неперервних сигналів:

за рівнем;
за часом;
змішане (за рівнем і за часом).

В залежності від використаного типу квантування неперервного сигналу дискретні системи поділяються на:

релейні (квантування за рівнем);
імпульсні (квантування за часом);
цифрові (змішане квантування).

Відносно задач синтезу та аналізу ІСАУ можуть бути поділені на:

лінійні;
нелінійні.

Нелінійні IСАУ підрозділяються на:

системи з лінійною неперервною частиною та нелінійним імпульсним елементом (ІЕ);
системи з нелінійною неперервною частиною та з лінійним ІЕ;
системи з нелінійною неперервною частиною та ІЕ.

В залежності від виду використаної в системі модуляції (процес квантування неперервного сигналу в ІС) або від типу ІЕ імпульсні системи поділяються на 4 класи:

Амплітудно-імпульсні (АІМ);
Широтно-імпульсні (ШІМ);
Фазо-імпульсні (ФІМ);
Частотно-імпульсні (ЧІМ).

АІМ: амплітуда А вихідної послідовності імпульсів змінюється у відповідності зі змінами вхідного сигналу. Тривалість τ і період повторення Т імпульсів постійні.

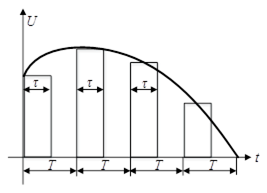
Рисунок 5.3 – АІМ

ШІМ: τ змінюється у відповідності зі змінами вхідного сигналу, а А і Т – const.

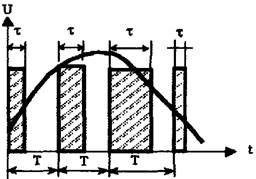
Рисунок 5.4 –ШІМ

Розглянемо приклад перетворення сигналів в ФІМ.

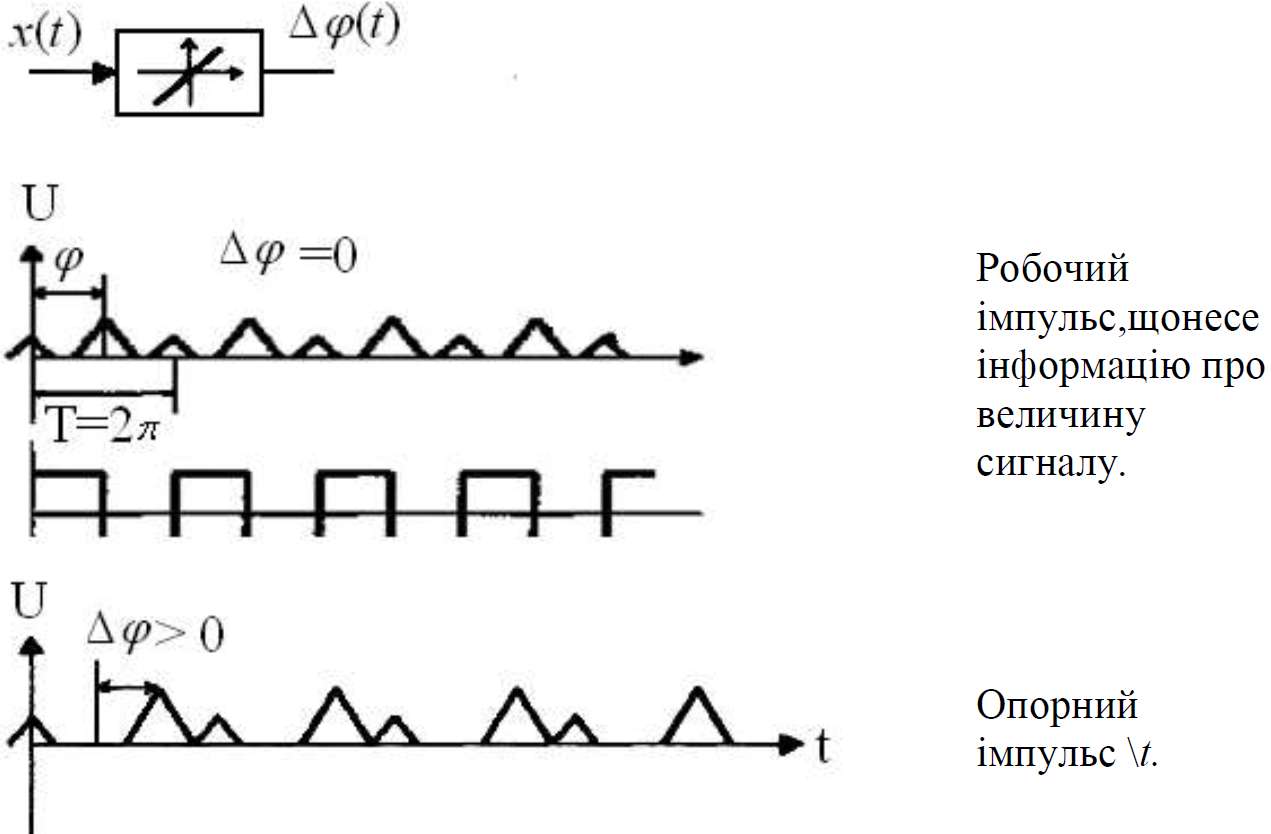
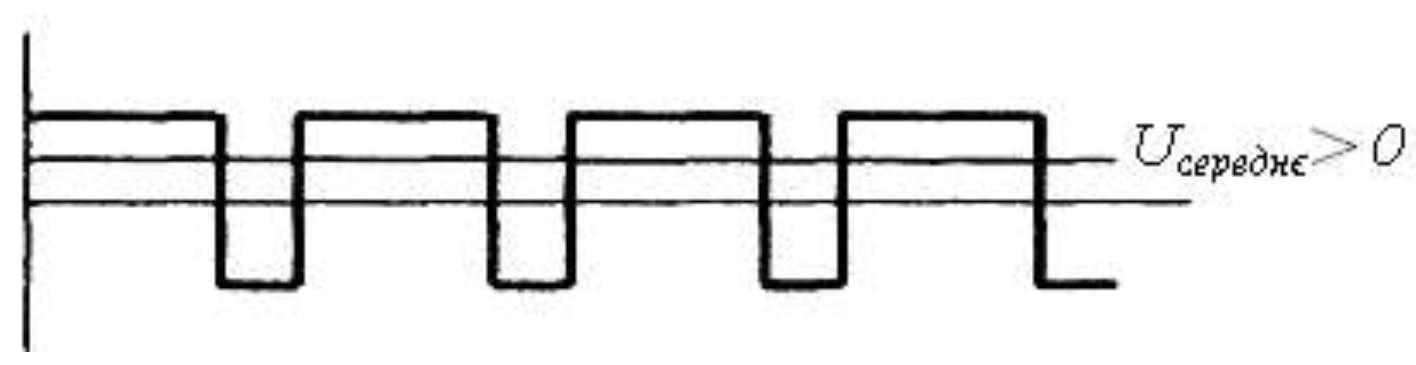
U_{середнє}= 0

При ФІМ змінюється фаза деякого імпульсу відносно опорного. Часто опорні імпульси мають постійну частоту. Імпульсна послідовність в ідеальному випадку повинна нести всю необхідну інформацію, що міститься в неперервному сигналі. Але при квантуванні за часом імпульсним елементом виділяються дискретні значення вхідного неперервного сигналу, що приводить до втрати частини інформації, вміщеної у вхідному сигналі. Цілком очевидно, що чим рідше квантується неперервний сигнал, тим важче відновити його форму після перетворення в ІЕ. Тому вибір частоти переривання ІЕ повинен відбуватися в залежності від форми вхідного сигналу, а дискретність квантування не повинна приводити до втрат інформації при проходженні неперервного сигналу через ІЕ.

Умови для вибору частоти переривання ІЕ визначаються на основі теореми Котельникова-Шеннона.

Теорема Котельникова-Шеннона

Неперервний сигнал х(t) з обмеженим частотним спектром в межах від 0 до F_с повністю визначається послідовністю своїх дискретних значень, що виникають через інтервал переривання (або частоту переривання – ).

Суть теореми полягає в тому, що неперервний сигнал може бути відновлений після квантування в ІЕ без спотворення, якщо частота квантування в 2 рази або більше перевищує граничну частоту в спектрі неперервного сигналу.

5.3 Динаміка ІСАУ.Поняття про решітчасті функції та різницеві рівняння

Якщо неперервний сигнал може бути представлений неперервною функцією часу, то сигнал на виході ІЕ може бути представлений тільки частиною значень неперервної функції. Ці значення розділені періодом квантування, а в середині періодів всі проміжні значення тільки нульові.

Тому дискретно представлені сигнали зручніше описувати функціями дискретної, а не неперервної змінної. Функцію, отриману в результаті заміни неперервної змінної дискретною незалежною змінною і визначену в дискретні моменти часу nТ, (n+1)Т,... називають решітчастою функцією.

На відміну від неперервної функції х(t) решітчасту функцію позначають як х[nТ]. Неперервна функція х(t) є огинаючою для своєї решітчастої функції х[nТ], але оскільки через дискретні точки решітчастої функції можна провести безліч огинаючих, то не існує зворотної однозначної відповідності між решітчастою функцією та її неперервною функцією. Ця обставина не дозволяє вважати решітчасту функцію повним аналогом неперервної функції.

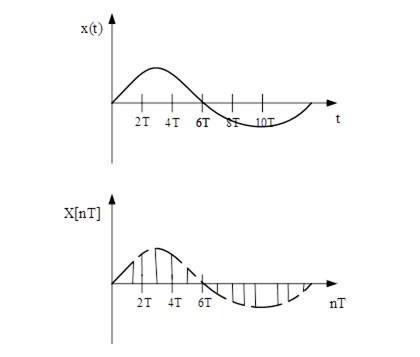
Поняття решітчастої функції лежить в основі спеціалізованого апарату опису дискретних систем і дозволяє здійснювати перехід до дискретного аналогу диференціальних рівнянь – різницевих рівнянь.

5.4 Приклад використання ЦОМ в якості регулятора.Редукція до неперервної САУ

Коли з'являються нові можливості, новий клас систем, то звичайно намагаються застосувати ці можливості в рамках старих систем, синтезувати нові системи старими методами, звести (редуціювати) до старих освоєних систем.

Згадайте перші автомобілі – карети з мотором; перші електродвигуни – пристрої типу парової машини із соленоїдом замість циліндра.

В методологічному аспекті даний приклад відноситься саме до такого класу підходів.

Розглянемо принципи реалізації неперервного регулятора за допомогою імпульсного пристрою ЦОМ.

Припустимо, що для неперервної системи вирішена задача синтезу і отримана передаточна функція регулятора:

При умові, що частота квантування в багато разів більше власних частот лінійної частини, дана функція може бути реалізована за допомогою ЦОМ. З урахуванням припущення про незначимість Т можливо похідні замінити кінцевими різницями, тобто:

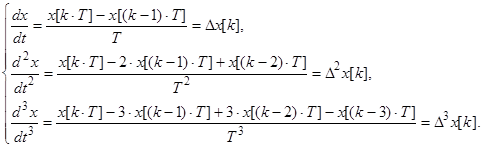
Запишемо диференційне рівняння, яке відповідає W_р, використавши обернене перетворення Лапласа:

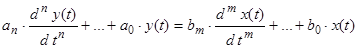Замінимо похідні кінцевими різницями і врахуємо зв'язок останніх з дискретними значеннями решітчастої функції:

Розв’яжемо знайдене рівняння відносно поточного виходу та отримаємо алгоритм роботи управляючої ЦОМ.

Таким чином, для реалізації W_ky необхідно зберігати в пам'яті m попередніх значень входу та n попередніх значень виходу.

Отже, ми розглянули приклад використання ЦОМ в якості регулятора, зробивши припущення про те, що внаслідок малості кроку квантування за часом Т, неперервні частини САУ “не помічають” дискретності роботи регулятора. Теоретичним фундаментом для цього підходу є теорема Котельникова-Шеннона:

Якщо неперервна частина САУ має обмежений зверху спектр (частотна характеристика), то існує кінцева частота квантування, при якій не відбувається втрат інформації в ЦОМ.

Чи обмежена область застосування ІСАУ тільки такою, заснованою на теоремі Котельникова-Шеннона, заміною неперервних систем ?

З досвіду управління складними нелінійними об'єктами відомо, що можливо так підібрати період і величину імпульсних впливів (так узгодити їх з динамікою об'єкта), що САУ буде нормально функціонувати. Однак при цьому виявляється, що ІСАУ в цьому випадку можуть мати властивості (як “добрі” так і “погані”), які не виводяться з властивостей неперервних САУ.

Наприклад, нехай виміряні значення виходу ІСАУ мають вигляд:

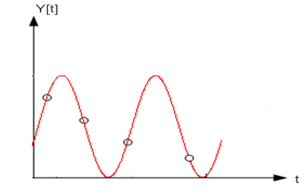
Рисунок 5.5 – Виміряні значення виходу ІСАУ

Чи стійка САУ? Цей приклад показує, що проблема стійкості ІСАУ має свої особливості в порівнянні з проблемою стійкості неперервних САУ.

Таким чином, для вирішення задач аналізу і синтезу ІСАУ необхідний власний математичний апарат, бажано подібний до вже засвоєного математичного апарату неперервних САУ.

5.5 Z перетворення

Виконаємо перетворення Лапласа:

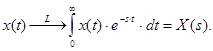
Виведемо дискретне перетворення Лапласа для ступінчатої функції.

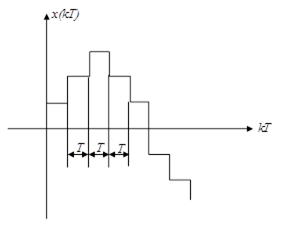
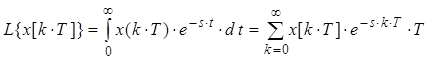Отже, ми розбили інтеграл на інтервали Т, на яких функція х(t) стала, і замінили інтеграл сумою.

Z-перетворення визначається наступним чином:

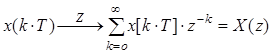Якщо вважати , то z-перетворення з точністю до Т співпадає з дискретним перетворенням Лапласа.

Приклад:

x[0]= -1
x[1]= 0
x[2]= -3
x[3]= 2
x[4]= 6

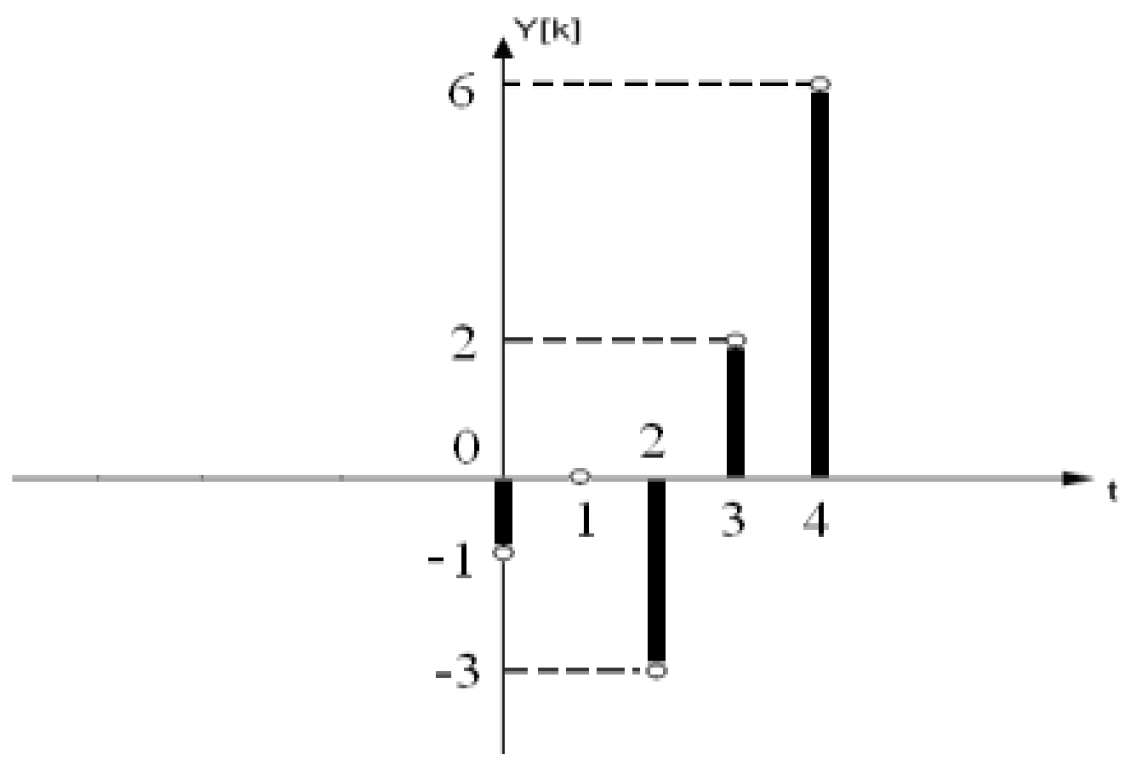
Отримаємо степеневий ряд для деякої змінної Z.

5.5.1 Властивості Z – перетворення

1) Лінійність:

а) .

б) .

2) Зміщення:

а) оригінала в області аргумента:

, якщо .

б) незалежної змінної в області зображення: зсув аргументу z в зображенні на ціле число періодів в комплексній області відповідає множенню z на , де n – ціле число. При множенні z на необхідно помножити оригінал x[kT] на , тобто:

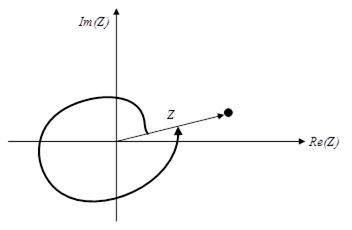
3) Диференціювання зображення:

Множення решітчастої функції x[kT] на kT відповідає диференціюванню її z зображення X(z), результат якого повинен бути помножений на -Tz, тобто:

4) Обернене Z-перетворення:

де z – комплексна змінна.

Дуже важливі для практики деякі наслідки властивостей z-перетворення. В чисто імпульсних системах немає сенсу говорити про інтеграл і похідну, але їх роль виконує сума і різниця значень імпульсної функції.

5) Z-перетворення від різниці:

– це аналог s•X(s).

6) Z-перетворення від суми:

– це аналог

Знайдемо z-перетворення від суми всіх відліків, включаючи поточне значення:

При виконанні z-перетворення:

– сума нескінченно–спадної

геометричної прогресії.

Завдання для самостійної роботи

Знайти z-перетворення наступних функцій:

1) одинарний імпульс :

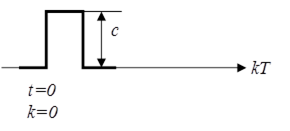
2) ступінчата решітчаста функція:

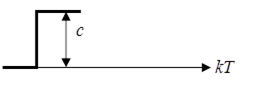
3) решітчаста функція з постійним нахилом:

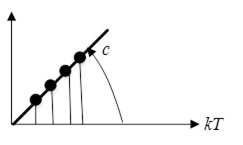
4) експоненціальна решітчаста функція:

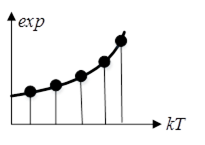
(t=kT для дискретного параметра).

5.5.2 Застосування Z-перетворення для розв’язання лінійних різницевих рівнянь

Різницеве рівняння для поточних координат х та у має вигляд:

Застосуємо z-перетворення (коефіцієнти А та В вважаємо сталими):

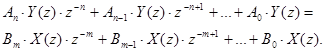
Винесемо за дужки Y(z) та X(z) і розв’яжемо отримане рівняння відносно Y(z):

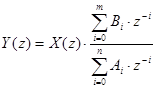– аналог Y(s)=X(s)•W(s).

Для знаходження початкової решітчастої функції y[kT] використовується обернене z-перетворення:

5.5.3 Z-передаточні функції розімкнених імпульсних систем

Розглянемо ІС без фіксатора (фіксуючий елемент – ФЕ):

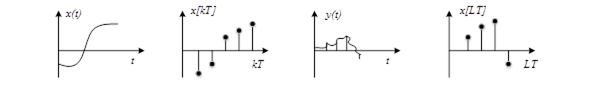
Y(z)=W(z)• X(z) – якщо б не було ІE.

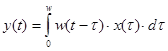– інтеграл згортки (зв'язує вихід і вхід системи);

– імпульсна перехідна функція для системи з W(S).

Для решітчастої функції y[LT]:

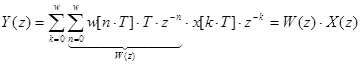5.5.4 Z-передаточна функція імпульсної системи з фіксатором 0-го порядку

На відміну від попереднього випадку, послідовність імпульсів після ІЕ перетворюється фіксуючим елементом (ФЕ) в ступінчастий сигнал:

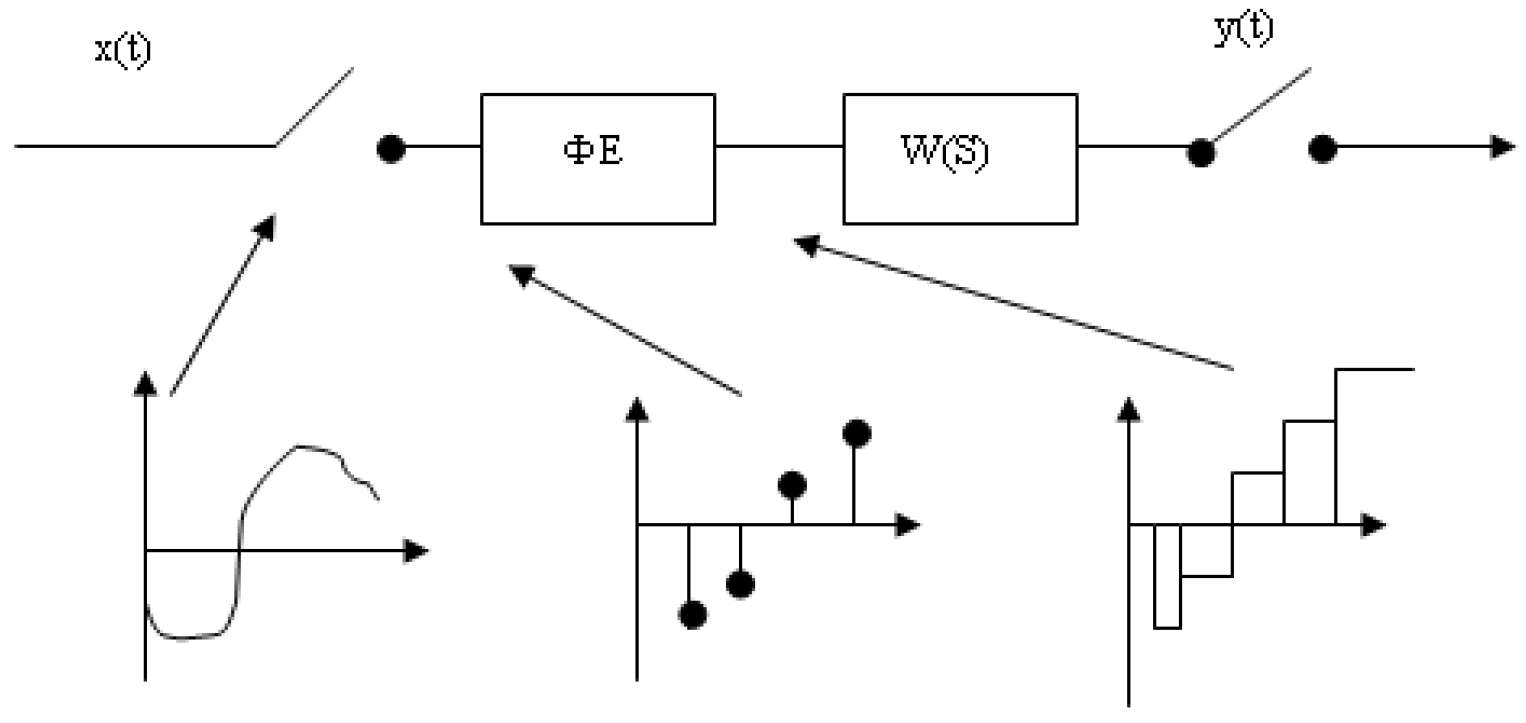
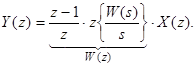(Виведіть самостійно!)

Правила отримання Z-передаточної функціх за W(s)

Для отримання z{W(s)} необхідно:

1) Отримати w(t);

2) Отримати w(nT);

3) За формулами z-перетворення для функції w(nT) знайти W(z).

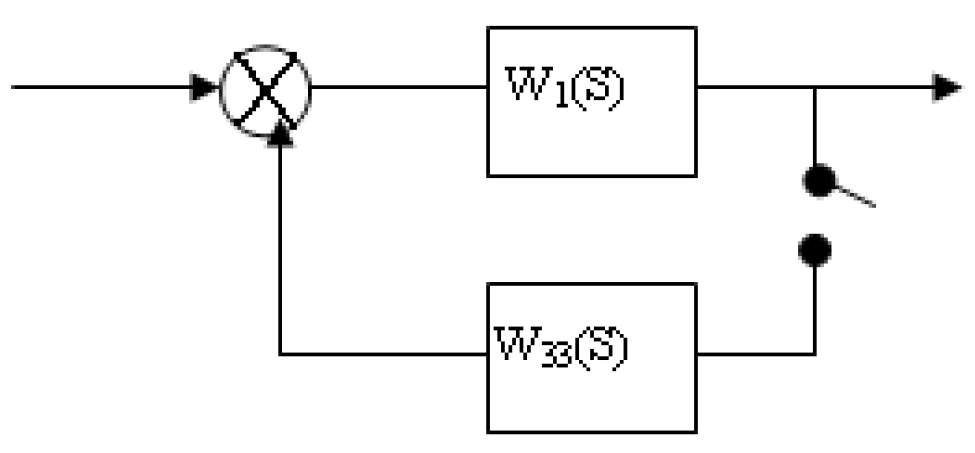
5.5.5 Передаточні функції замкнених ІСАУ

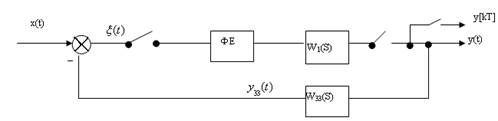
Для отримання передаточної функції замкненої ІС використовуємо ту ж методику, що і при виведенні W _замкн(s) неперервних систем.

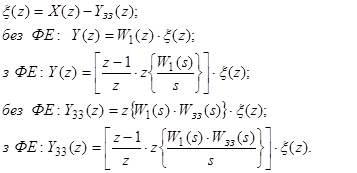
Використовуючи підстановку отримаємо початкові передаточні функції:

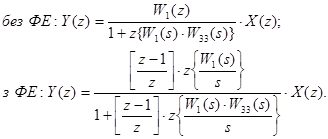
Для іншого положення імпульсного елемента (ключа) будемо мати інші вирази для передаточних функцій:

5.6 Стійкість ІСАУ

Розділ будемо розглядати по аналогії з розділом стійкості неперервних САУ.

Неперервні ЛДС	Лінійні ІСАУ
Дано:
Диференціальне рівняння:	Однорідне різницеве
(І)	(І)
Стійкість розглядаємо за відношенням до вільного руху (визначення за Ляпуновим). Розв’язання шукаємо у вигляді:
(ІІ)	(ІІ)
Підставляємо (II) в (I):
	скорочуємо на та множимо на zⁿ
Отримаємо:
s-xарактеристичне рівняння	z-характеристичне рівняня

Знаходимо корені:

Розв’язання отримали у вигляді:

Геометричне представлення коренів:

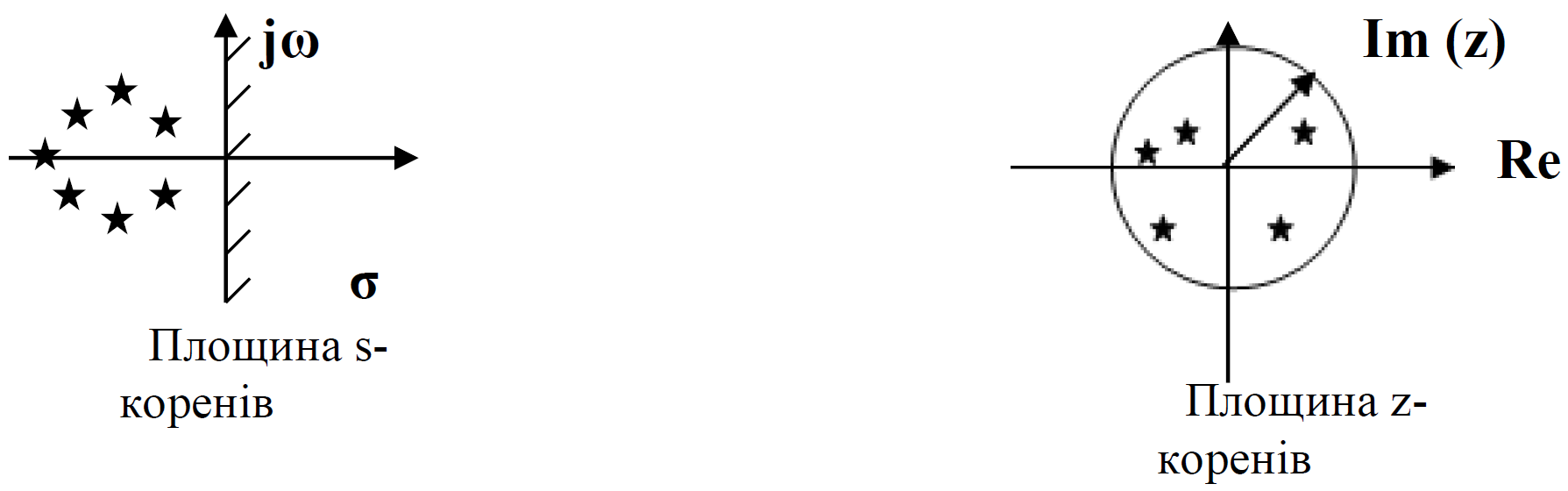
Необхідна та достатня умова стійкості:
Корені повинні бути “лівими”	Корені z-характеристичного рівняння повинні знаходитись в середині одиничного кола (тобто ).

В подальшому для уніфікації позначень будемо записувати z-характеристичне рівняння у вигляді:

Пам'ятайте, що коефіцієнти z-характеристичного рівняння не тотожні s-характеристичному рівнянню неперервної системи, вони пов'язані складними залежностями.

5.6.1 Критерії стійкості ІСАУ та метод білінійного перетворення

Таким чином, як і для неперервних лінійних САУ задача аналізу стійкості звелась до визначення місцезнаходження коренів. Також, як і в випадку неперервних систем бажано, не обчислюючи корені, визначати стійкість, тобто мати деякі критерії стійкості.

Для ІСАУ використовуються наступні критерії стійкості:

1) алгебраїчні :

- критерій Шура і Кона;

- іннортні критерії.

2) частотні:

- аналог критерія Михайлова;

- аналог критерія Найквіста.

3) методи зведення z-площини до s-площини:

- метод білінійного перетворення.

Формально метод білінійного перетворення зводиться до виконання наступних операцій:

1) В початковому z-характеристичному рівнянні:

замінимо змінну z на W у відповідності з:

Примітка: вочевидь, обернене перетворення має вигляд:

Після алгебраїчних перетворень отримаємо алгебраїчне рівняння n-го степеня для змінної W:

2) Якщо корені W-характеристичного рівняння знаходяться в лівій напівплощині, то система ІСАУ стійка.

Нам відомо, що необхідна та достатня умова стійкості неперервної САУ – ліві корені характеристичного рівняння. Для перевірки цієї умови існує достатня кількість критеріїв стійкості. Тому, для перевірки того, чи є корені W-характеристичного рівняння лівими, можна використати будь-які критерії стійкості лінійних неперервних САУ.

Розглянемо ідейний сенс білінійного перетворення.

Скажіть, як це перетворення зміщує точки на комплексній площині? Визначте самостійно куди перейдуть точки А₁(1; 0j), А₂(-1; 0j), В₁(0; j), В₂(0; -j), O(0; 0).

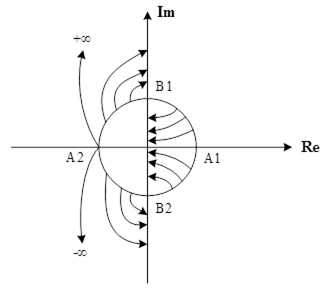
Неважко перевірити, що точки одиничного кола переходять в точки уявної осі; точки, які лежать всередині кола, – в точки лівої напівплощини; точки, які лежать за межами одиничного кола, – в точки правої напівплощини. Очевидно, що ліві W-корені при зворотному білінійному перетворенні виявляться всередині одиничного кола.

Практичний приклад:

Як спіймати лева в Сахарі ? (Л-лев. М- мисливець).

5.6.2 Критерій Шура і Кона

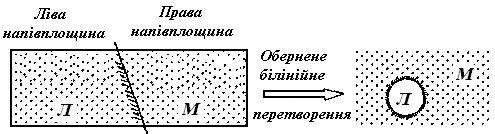
Шур і Кон – німецькі вчені, математики, які займалися (≈1900 р.) розглянутими, цікавими тоді тільки вузькому колу математиків, проблемами.

Дано:

Характеристичне рівняння:

Розв'язок:

1) Будуємо і обчислюємо визначники Δk , де , де n – порядок системи.

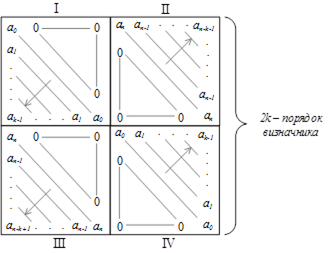
2) Матрицю розбиваємо на 4 блоки. Головну діагональ заповнюємо коефіцієнтами а, малі діагоналі (головні діагоналі в блоках II, III) заповнюємо коефіцієнтами а Верхні трикутники в блоках І, III та нижні трикутники в блоках II, IV заповнимо нулями. Верхній і нижній трикутники в блоках II, III заповнимо діагоналями коефіцієнтів , а нижній та верхній трикутники блоків І, IV заповнимо діагоналями коефіцієнти .

Побудуємо такі матриці для к=1, к=2, к=3.

k=1

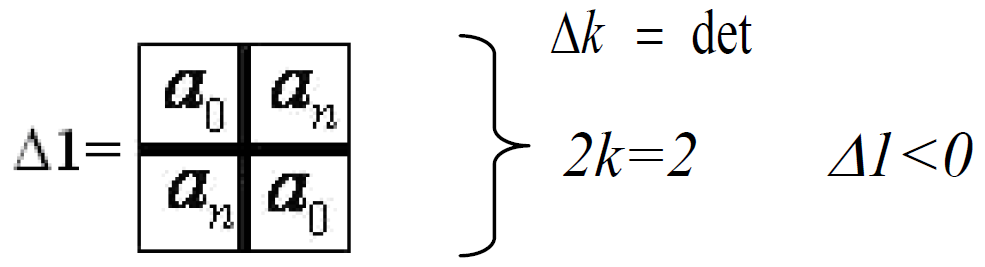
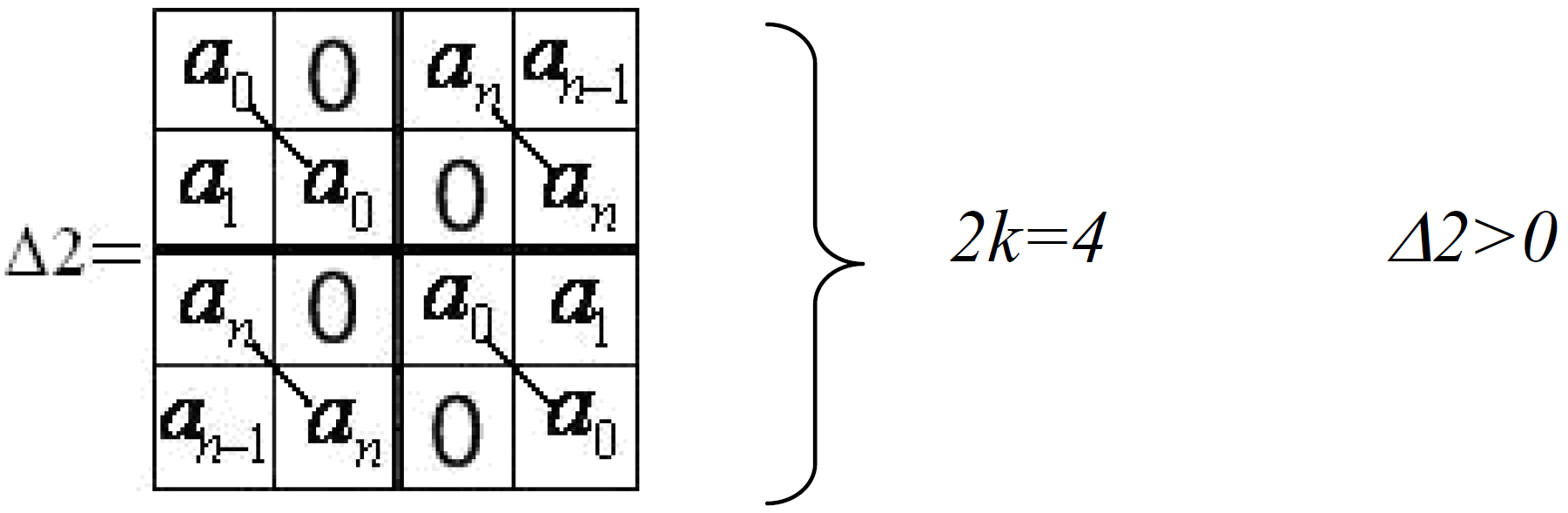
k=2

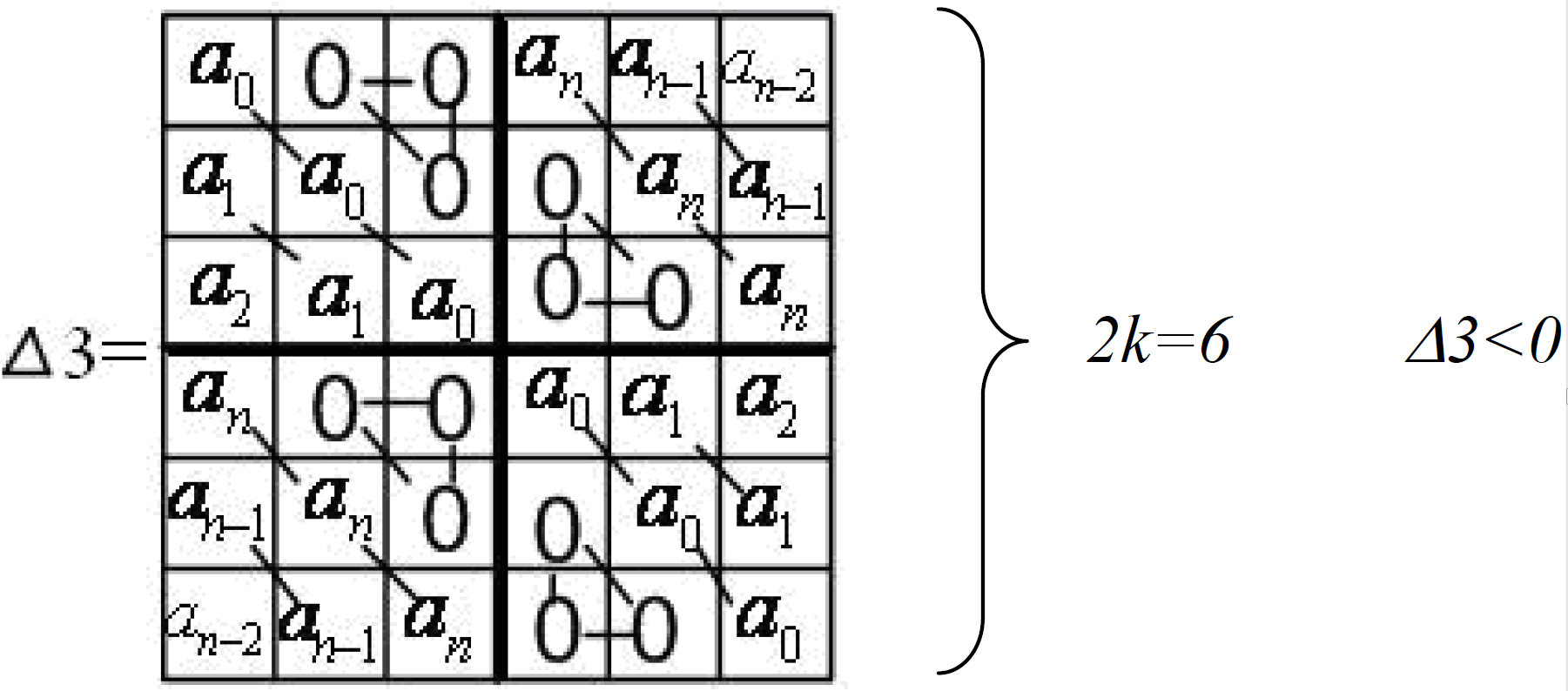
k=3

3) Перевіряємо на стійкість.

Необхідна та достатня умова стійкості:

Δk> 0, якщо k – парне;

Δk< 0, якщо k – не парне.

Завдання для самостійної роботи

Перевірте на стійкість ІСАУ, використовуючи критерій Шура і Кона, якщо характеристичне рівняння має вигляд:

а₃z³+a₂z²+a₁z+a₀=0,

де а,=3; a₂=-2; a₁=1; a₀=5.

5.6.3 Іннорні критерії стійкості

Проблема аналізу стійкості для неперервних і дискретних ЛДС зводиться до проблеми окремих коренів. Загальне формулювання умови стійкості: для стійкості САУ необхідно і достатньо, щоб корені відповідного характеристичного рівняння лежали в заданій частині комплексної площини:

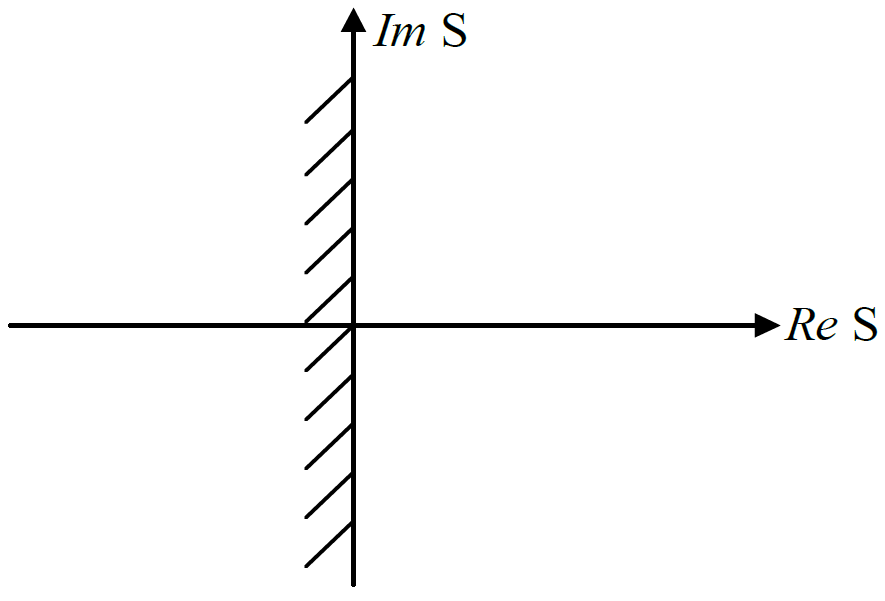
для НСАУ – це ліва напівплощина.

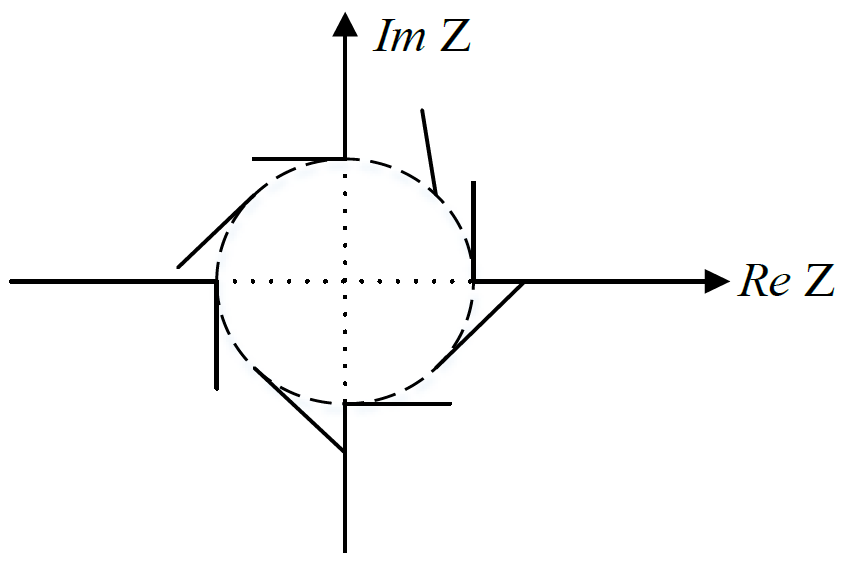
для ІАСУ – це одиничне коло.

Існують ще задачі, в яких ця область має інший вигляд. Наприклад, цифрові фільтри для зображень, так звані двовимірні фільтри. Практичні задачі, які вирішуються такими фільтрами:

1) очистка телевізійних та інших зображень від шумових завад;

2) відновлення “змазаних” знімків і кадрів.

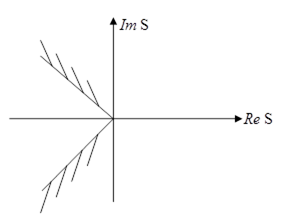
Двовимірні фільтри обробляють точки на площині, задані двома координатами. Характеристичне рівняння для таких систем має комплексні коефіцієнти. Деякі з таких фільтрів по-суті подібні спосте-рігачу. Умова стійкості для них може мати вигляд:

Таким чином, проблема стійкості – це проблема відділення коренів. Чи можливо створити загальні методи для визначення належності коренів довільного алгебраїчного рівняння деякій заданій області? Чи неможливо узагальнити алгебраїчні критерії Гауса-Гурвиця, Шура-Кона?

Можливий шлях цього узагальнення – іннорні методи.

Іннори в теперішньому інженерному вигляді запропоновані відомим американським вченим, професором Каліфорнійського університету в Берклі Е. Джурі в 1960-х роках, який в основному спирався на роботи Ерміта (1840 р.), Гурвиця (1870 р.), Шура і Кона (1910 р.), радянських вчених М.Г. Крейна, М.А. Неймарка (1936 р.), Я.З. Ципкіна (1950-1960 р.р.)

Іннорами називають певні квадратні підматриці будь-яких квадратних матриць порядку n.

Іннорна матриця — матриця певної конфігурації, складена з коефіцієнтів характеристичного рівняння D(s) або D(z).

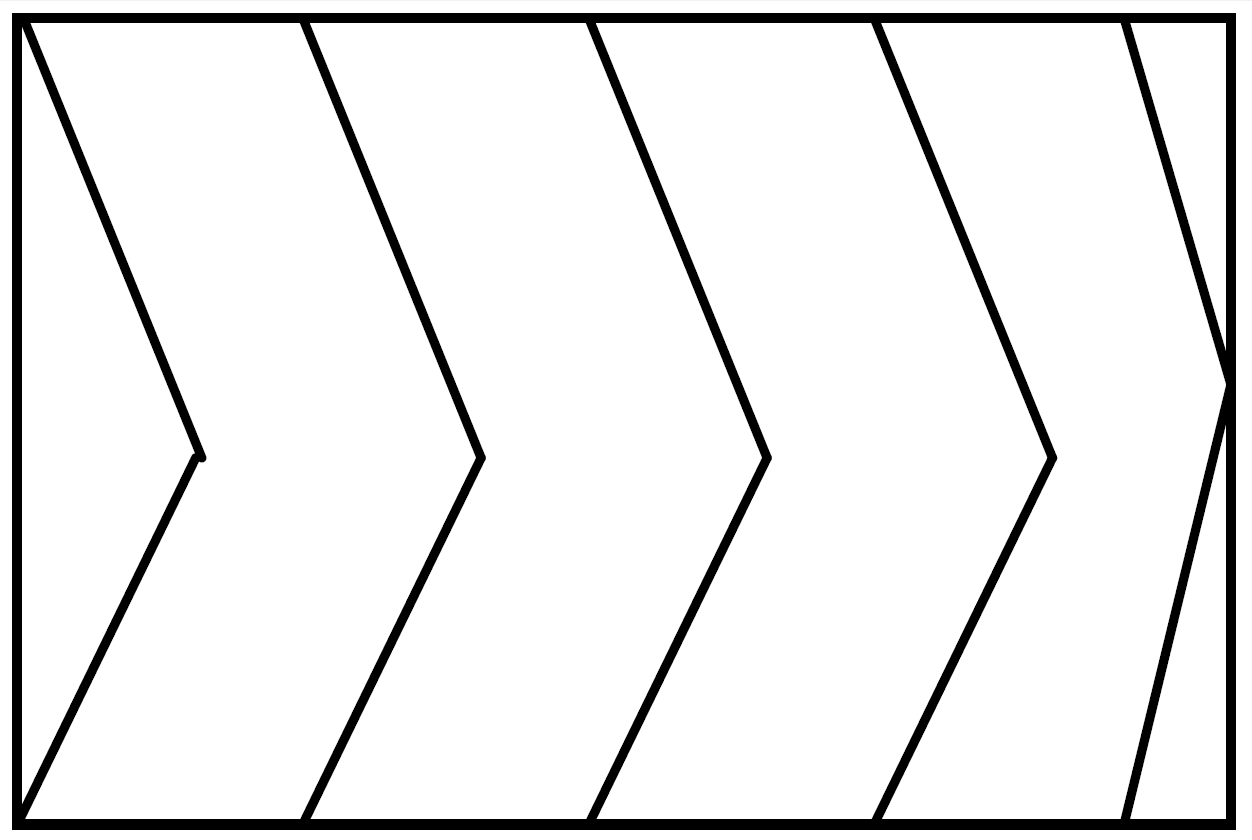
Іннор — визначник, отриманий з іннорної матриці викреслюванням крайніх рядків і стовпців:

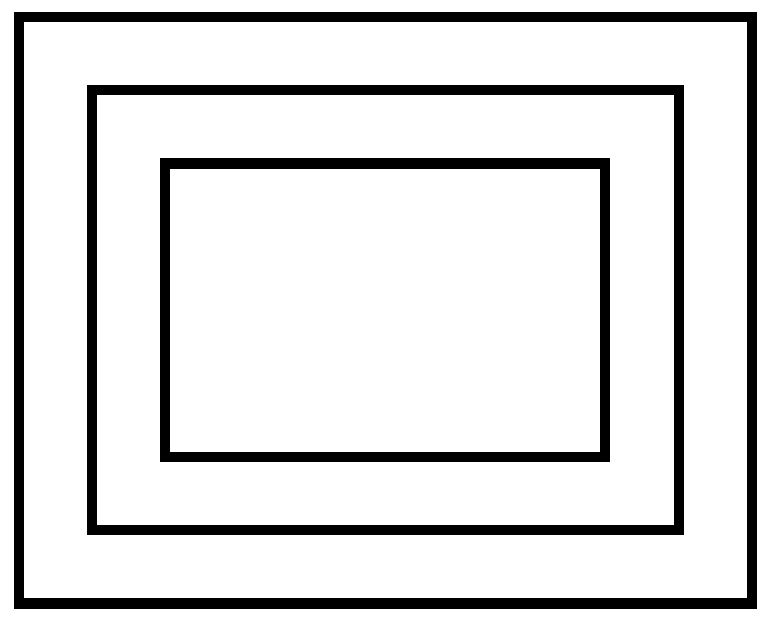
Розглянемо побудову іннорної матриці на прикладі системи 5-го порядку, тобто n=5:

Порядок іннорної матриці визначається з формули 2п-1, в даному випадку він дорівнює 9.

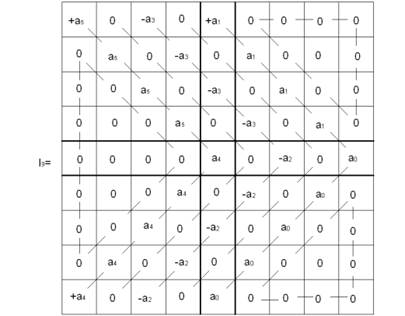
Порівняйте структуру визначників для критеріїв

5.6.3.1 Іннорний критерій стійкості для неперервних САУ

Іннорний критерій для неперервних САУ має вигляд:

для будь-яких j маємо det I_j > 0, j = 9,7,5,3,1.

5.6.3.2 Іннорний критерій стійкості для ІСАУ

1) Дано:

2) Підготовчі операції:

а) а_n > 0 (якщо менше нуля, то помножити (1) на число -1);

б) побудувати іннорні матриці X_n_-1 i Y_n_-1

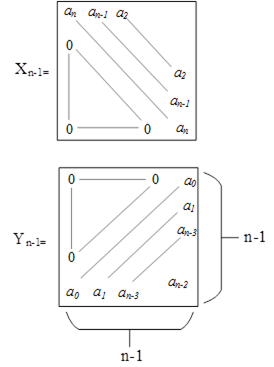
3) Перевірка стійкості, яка передбачає виконання одночасно трьох умов:

а) D(1)>0; (z= -1).

б) (-1)ⁿ •D(-1)>0; (z= -1).

в) det ¦X_n_-1 + Y_n_-1¦> 0.

Завдання для самостійної роботи

Перевірити на стійкість ІСАУ з використанням інорного критерій, якщо характеристичне рівняння має вигляд:

а) z⁷ + 1 =0

б) -3z⁵- 4z⁴+ 3z³-2z² – z - 1 =0

5.7 Багатовимірні САУ

Сучасні САУ, як правило, багатозв'язні, багатовимірні, оскільки навіть в граничному випадку, коли необхідно управляти єдиною змінною за допомогою єдиного управляючого впливу, оптимальне рівняння потребує врахування похідних, інтегралів від входу та виходу. Використовуючи канонічну формулу Коші для такої системи, ми подаємо її як багатовимірну.

Використовуючи накопиченні знання про неперервні багатовимірні САУ і базові відношення зв'язку неперервних та імпульсних динамічних систем, перейдемо до методів аналізу і синтезу багатовимірних ІСАУ.

Канонічне зображення багатовимірної неперервної САУ:

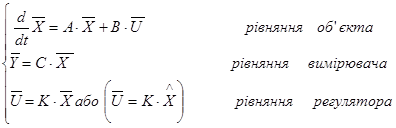
Для замкненої неперервної САУ:

Відомо, що розв'язок такої системи наводиться у вигляді:

(5.1)

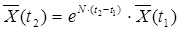
Для матричної експоненти відоме розкладання в ряд:

(5.2)

Використаємо (5.1) і (5.2) в якості базової ланки, яка зв'язує неперервні та імпульсні динамічні системи.

Нехай t₂- t₁= T період квантування в ІСAУ, тоді

де F(Т) – перехідна функція стану для ІСАУ з періодом квантування Т.

З урахуванням цього позначення маємо:

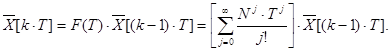
Аналогічне рівняння можемо отримати і для розімкненої ІСАУ.

Для розімкненої системи:

Залежність виходу в поточний момент від попереднього значення і зовнішнього (в даному випадку управляючого) впливу має вигляд (див. теорію лінійних диф. рівнянь):

(5.3)

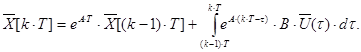
Якщо Т достатньо мале, так що для , то:

(5.4)

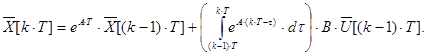
Інтеграл в даному виразі може бути представлений наступним чином:

(5.5)

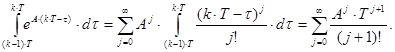
Завдання для самостійної проробки:

Використовуючи свої знання з курсу вищої математики, зведіть даний визначений інтеграл до табличного вигляду:

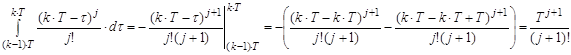
Підставляючи (5.5) в (5.4), отримуємо:

(5.6)

де

(5.7)

(5.8)

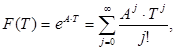
Вираз (5.8) справедливий, якщо А не вироджена.

Вирази (5.6), (5.7), (5.8) — основа для побудови обчислювальних алгоритмів моделювання і управління.

Зокрема вирази для матриць F(T) і G(T) можна обраховувати рекурентно.

(5.9)

(5.10)

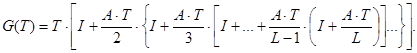
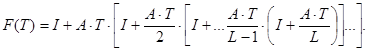
Тут L — кількість доданків в апроксимації G(Т) і F(T ).

Формули (5.9) і (5.10) (наведені для довідки) дозволяють поставити задачу оптимізації кроку квантування.

Якісні міркування по вибору Т формулюються наступним чином.

При використанні малих Т для отримання заданої точності в (5.9) і (5.10) не вимагається брати більше 1-2 доданків.

Загальні витрати обчислювальних ресурсів (пам'яті, швидкодії) на управління і (або) моделювання ІСАУ складаються з витрат на обчислення G(Т) і F(Т) та витрат на обчислення на кожному кроці (наприклад, за формулою 5.6). Перша складова зростає зі зростом Т, друга — спадає. Формально, якщо А, В постійні і відомі абсолютно точно, мінімуму обчислювальних витрат відповідає (G(T), F(T) — обчислюються в цьому випадку тільки один раз, до початку функціонування системи). Для реальних САУ А і В — змінні, які відомі приблизно, тому немає сенсу вибирати великі Т, існує 0 <Т _опт <.

Z – характеристичне рівняння багатовимірної ІСАУ

Неуправляєма САУ:

Застосуємо z-перетворення для цього рівняння:

Після алгебраїчних перетворень:

(5.11)

Рівняння (5.11) – це в згорнутому вигляді система лінійних однорідних рівнянь, яка має нетривіальне () розв’язання, якщо:

Після розкриття визначника отримаємо поліном від z — шукане характеристичне рівняння.

Аналогічно, отримаємо z-характеристичне рівняння для управляємої САУ:

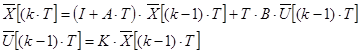
і спостерігача:

неперервне рівняння:

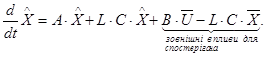або однорідне рівняння:

дискретне рівняння:

z—характеристичне рівняння:

5.8 Управління з кінцевим часом встановлення (УКЧВ). Спостерігач з кінцевим часом встановлення (СКЧВ)

Як вже говорилося на початку розділу, ІСАУ не є всього лише ерзац-замінювачем, наближенням до неперервних САУ, в них є властивості, які відсутні в неперервних САУ.

Особливість неперервних лінійних САУ з лінійними законами управління по вектору стану — асимптотичність — стан, що встановився (необхідний), досягається за нескінченний час:

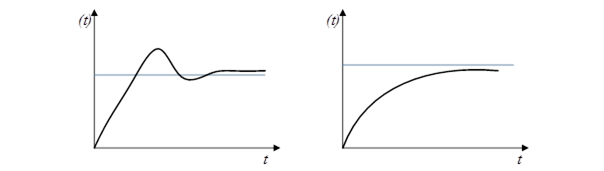
Процеси, графіки яких наведені нижче, для них неможливі:

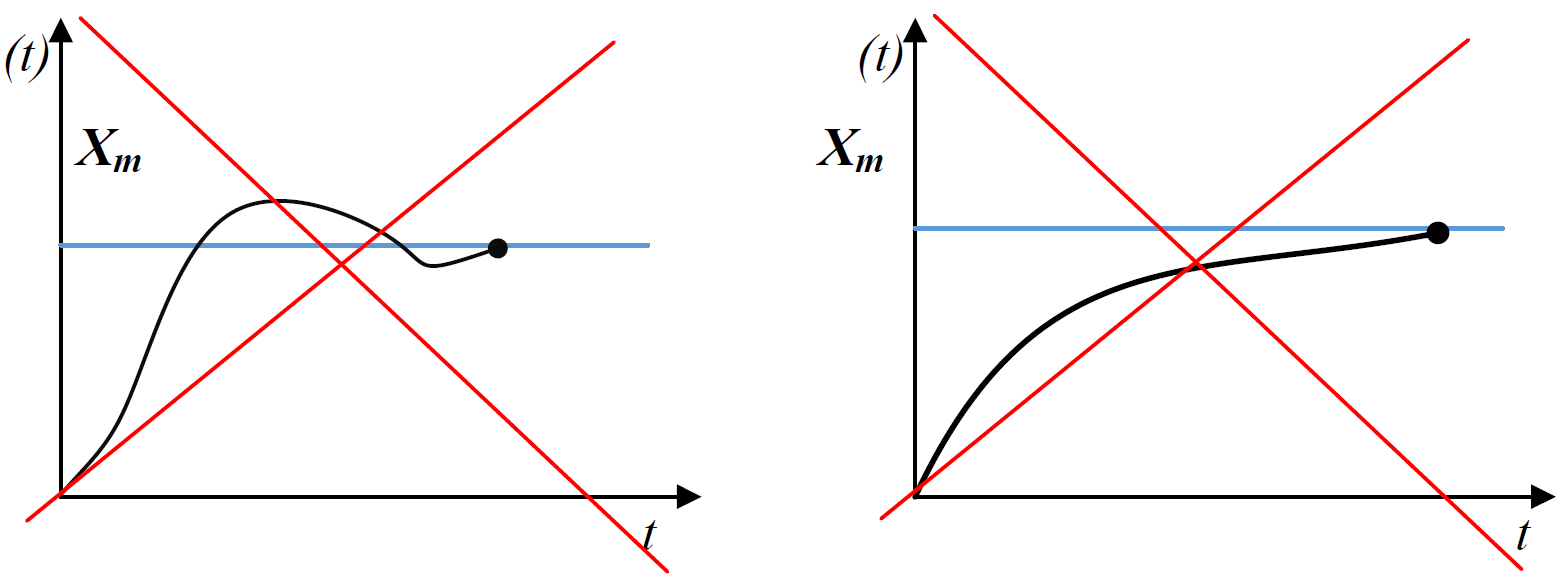
Для ІСАУ можна так підібрати параметри закону управління:

що перехідні процеси будуть закінчуватись не більш, ніж за n кроків квантування (n – порядок системи).

На жаль, термінологія відстає від технічного прогресу. Регулятори з такими властивостями називають:

“УКЧВ – регулятор” (управління з кінцевим часом встановлення)
“СКЧВ – спостерігач” (спостерігач з кінцевим часом встановлення).
“швидкий регулятор” (не плутайте з швидкодіючим регулятором).
“швидкий спостерігач” (не плутайте з швидкодіючим спостерігачем).
“короткий регулятор”.
“аперіодичний регулятор”.
до цього класу понять та методів відноситься і ще більш невдалий термін – загальновідомий ШПФ (швидкий перетворювач Фур'є).

Спробуйте підібрати більш вдалі терміни.

Розглянемо проблему КЧВ (кінцевого часу встановлення) чисто фено-менологічно, “поекспериментуємо” з математичною моделлю ІСАУ.

Нехай задана довільна імпульсна динамічна система 7 порядку:

Для послідовності кроків k = 0, 1, 2,... квантування Т будемо випускати в аргументі, тоді можемо записати:

…

Виключивши проміжні змінні, отримаємо:

В загальному вигляді:

З теорії матриць відомо [Сигорський, Коршунов та ін.], що якщо всі власні числа (тобто корені характеристичного рівняння дорівнюють нулю):

то

— матриця зі всіма нульовими

елементами.

Зокрема, матриці виду “з наддіагоналлю з одиниць та іншими нулями” мають нульові власні числа:

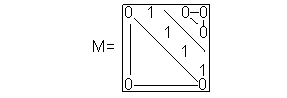
Спробуйте послідовно помножити таку матрицю саму на себе. Діагональ з одиниць (одиниці взяті для простоти прикладу) буде переміщуватися вправо і на n-ому кроці “зникне”:

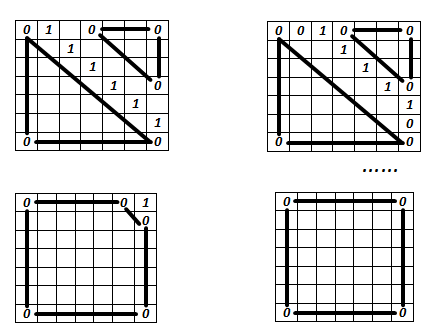
Таким чином, якими б не були компоненти вектора не пізніше, чим на п-ому кроці .

Перехідні процеси по компонентам будуть мати вигляд (показані тільки 3 із 7 компонентів, щоб не загромаджувати рисунок):

5.8.1 Синтез УКЧВ і СКЧВ

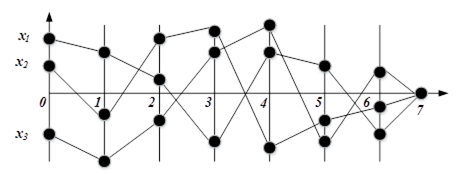
Розглянемо необхідну та достатню умову управління з кінцевим часом встановлення. Z-характеристичне рівняння ІСАУ:

тому необхідна і достатня умова УКЧВ будь-яких де :

що можливо, якщо характеристичне рівняння має вигляд:

тобто всі коефіцієнти а_n_-1..., a₀ дорівнюють нулю.

Формально процедура синтезу УКЧВ буде наступною.

Дано:

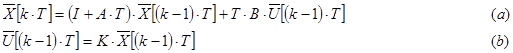
Визначити: К — матрицю параметрів регулятора, яка забезпечує УКЧВ.

Подана задача аналогічна розглянутій раніше задачі синтезу управління по вектору стану методом стандартних коефіцієнтів.

Розв'язання:

1) Підставляємо (b) в (a), маємо:

2) Запишемо z-характеристичне рівняння:

3) Розкриємо визначник:

Коефіцієнти а_n,...,а₀ очевидно будуть функціями від елементів матриць А, В (відомих) і К (шуканої).

4) Прирівняти до нуля всі коефіцієнти (крім а_n), отримаємо n рівнянь для невідомих елементів матриці К, де а :

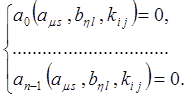
В поданій обмеженій постановці задача має велику кількість розв'язків.

Очевидно, що для системи з одним управляючим впливом розв'язок буде однозначним.

При синтезі реальної ІСАУ з КЧВ об'єктом вибору є не тільки параметри матриці К (у випадку системи з одним входом (m=1) матриця К вироджується у вектор), але і період квантування. При зменшенні періоду квантування Т необхідні значення управління зростають. Чому? Це зрозуміло з наступного рисунка:

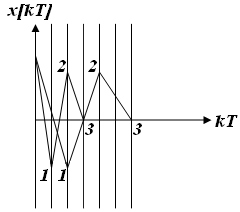
Прикладні питання синтезу УКЧВ і СКЧВ для систем з одним входом і одним виходом розглянуті в працях авторів таких, як Ізерман, Шатолов; для загального випадку — багатовимірної системи — в [ЗИ №21, 1979, реф. 107 К. Ісhіkаnа «Дискретний “швидкий” регулятор зі “швидким” спостерігачем»].

5.8.2 Область застосування УКЧВ і СКЧВ та особливості синтезу

Розрахунок параметрів УКЧВ і СКЧВ в переважній кількості випадків дуже простий, він може виконуватися навіть на кожному окремому такті управління ІСАУ заново. В зв'язку з цим УКЧВ і СКЧВ перспективні в адаптивних (самоналагоджуючихся, самонавчальних, самонастроювальних...) ІСАУ, які змінюють параметри регулятора (матриці К) у відповідності з параметрами об'єкта (А, В, С). Однак, “дивні” властивості (а в техніці див не буває, оскільки за все треба платити) КЧВ досягаються фактично скороченням чисельника (знаменника) z-передаточної функції.

Якщо корені неуправляємого об'єкта лежать близько від одиничного кола, то така система буде дуже чутливою (“негрубою”) до помилок визначення А, В, С. Тому застосування КЧВ обмежується класом асимптотично стійких [див. Ізерман] об'єктів управління.

Контрольні запитання

Визначення поняття стійкості по Ляпунову.
Необхідна і достатня умови стійкості ЛДС.
Формулювання критерія Найквиста.
Формулювання критерія Михайлова.
Формулювання критерія Гурвиця.
Як можна знайти корені лінійного алгебраічного рівняння N-ступеню.
Що таке "характеристичне рівняння"?
Що таке "кореневий годограф", як можна по кореневому годографу визначити нестійкість САУ?
Що таке "запас стійкості по фазі", "запас стійкості по амплітуді"