Попередня сторінка Зміст Наступна сторінка Електронні посібники ВНТУ
6 АНАЛІЗ І СИНТЕЗ НЕЛІНІЙНИХ ТА РЕЛЕЙНИХ САУ
6.1 Нелінійні системи. Визначення. Класифікація. Характеристики нелінійних систем
6.2 З’єднання нелінійних ланок
6.3.1 Властивості фазових траєкторій
6.3.2 Класифікація особливих точок
6.4 Стійкість нелінійних систем
6.4.2 Абсолютна стійкість. Критерій абсолютної стійкості В. М. Попова
Література по темі розділу — другі частини підручників Воронова і Нетушила, а також відповідні розділи нашої електронної книги (релейні САУ).
Ви пам’ятаєте з першої частими курсу, що лінійні системи складають десь 5-10% від усіх САУ, що зустрічаються в практиці інженера. Для лінійних систем є загальні методи аналізу і синтезу.
Сьогодні ми переходимо до вивчення нелінійних систем, що складають 90%. Для нелінійних систем таких загальних методів не існує. Ви можете заперечити - є другий метод Ляпунова аналізу стійкості нелінійних систем. Але цей метод не є вичерпним рецептом і алгоритмом - там треба спочатку винайти або сконструювати функцію Ляпунова. Загальних рутинних методів для нелінійних систем не існує.
Чому ми так пізно починаємо вивчати нелінійні САУ?
1. Тому, що це відповідає програмі курсу.
2. Тому, що це відповідає традиціям ТАУ
3. Тому що ми їх вже давно вивчаємо: перша частина почалась з лінеаризації.
Потім на протязі семестру ми вивчали фактично поведінку нелінійних систем при малих відхиленнях від номінальних режимів.
Тепер переходимо до безпосереднього вивчення нелінійних систем.
6.1 Нелінійні системи. Визначення. Класифікація. Характеристики нелінійних систем
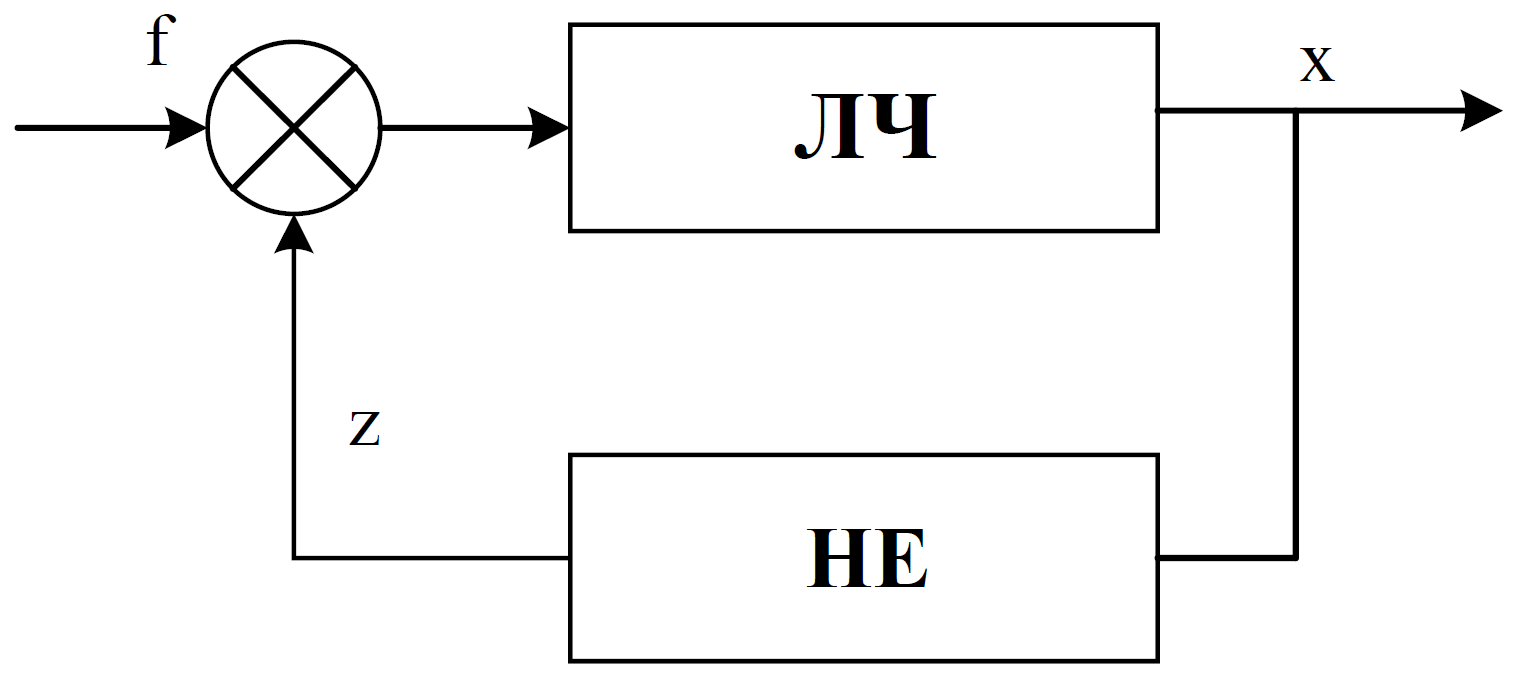 До нелінійних систем відносять всі системи, які не можуть бути описані лінійними диференціальними рівняннями. Множина нелінійних систем настільки широка і різноманітна, що практично не можна говорити про єдиний клас нелінійних систем, що протистоїть класу лінійних систем. Розглянемо більш вузький, але широко розповсюджений в практиці управління, клас нелінійних систем, що характеризуються наступними особливостями: систему можна представити у вигляді з'єднання двох частин – лінійної частини ЛЧ, що описується лінійними звичайними диференціальними рівняннями зі сталими коефіцієнтами, і нелінійного елементу НЕ.
До нелінійних систем відносять всі системи, які не можуть бути описані лінійними диференціальними рівняннями. Множина нелінійних систем настільки широка і різноманітна, що практично не можна говорити про єдиний клас нелінійних систем, що протистоїть класу лінійних систем. Розглянемо більш вузький, але широко розповсюджений в практиці управління, клас нелінійних систем, що характеризуються наступними особливостями: систему можна представити у вигляді з'єднання двох частин – лінійної частини ЛЧ, що описується лінійними звичайними диференціальними рівняннями зі сталими коефіцієнтами, і нелінійного елементу НЕ.
Нелінійний елемент є безінерційним, і його вхідна X і вихідна Y величини зв'язані між собою нелінійними алгебраїчними рівня-ннями. Таким чином, нелінійність систем, що розглядаються, обумовлена нелінійністю статистичної характер-ристики одного з її елементів.
Приклади нелінійних елементів:
1) Двофазний асинхронний двигун;
2) Тріод;
3) Гідропривід;
4) Магнітній підсилювач;
5) Аеродинамічні рулі літаючих апаратів.
Класифікація нелінійностей
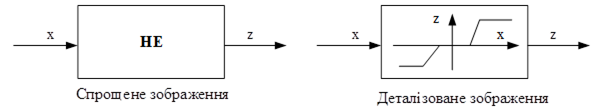
Нелінійності діляться на:
статичні: ![]() ;
;
динамічні: 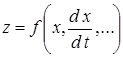 .
.
Статичні нелінійності можна класифікувати по слідуючим показникам:
1) симетрія:
а) чітко симетричні (симетричні відносно осі ординат);
б) нечітко симетричні (симетричні відносно початку координат);
в) несиметричні;
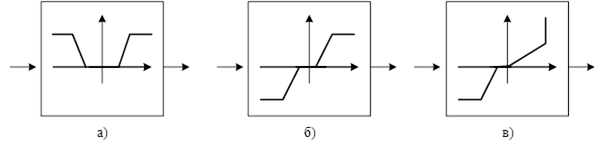
2) гладкість:
· гладкі;
· ламані (кусочно-лінійні).
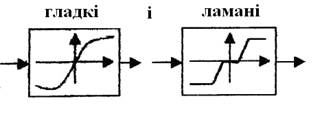
3) однозначність:
· однозначні;
· багатозначні.
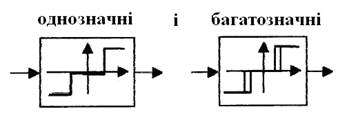
Типові нелінійності
В першій частині для лінійних систем ми розглядали типові елементарні ланки – «алфавіт лінійних систем».Аналогічний «алфавіт» існує і для статичних нелінійностей.
Довільну статичну нелінійність можна скласти з типових.
Вибір „типових” нелінійностей базується на практиці – типовими вважаються ті нелінійності, що найчастіше зустрічаються в інженерній практиці. Розглянемо послідовно ці типові нелінійності.
1) "Зона нечутливості".
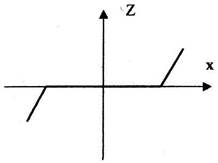
Такими характеристиками володіють деякі схеми електричних, магнітних та гідравлічних підсилювачів в області малих вхідних сигналів.
2) "Обмеження" (або "насичення").
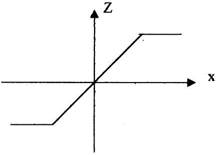
Подібними характеристиками володіють практично всі реальні підсилювачі, обмежені в області великих вхідних сигналів по потужності.
3) "Обмеження з зоною нечутливості".
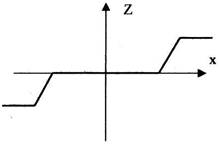
При малих вхідних сигналах ланка поводить себе подібно до ланки типу "зони нечутливості", а при великих – ланки типу "обмеження".
4) "Гістерезис".
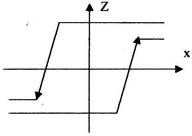
Двохпозиційне, трьохпозиційне реле з гістерезисом.
5) "Люфт".
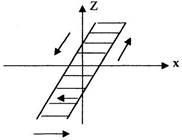
Найбільш часто зустрічаються в механічних системах та пов'язані з наявністю зазорів в системі передачі (кермо автомашини).
6) "Упор".
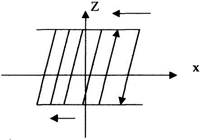
В механічних системах переміщення однієї з частин обмеженої в двох напрямках, при цьому ведуча частина може необмежено переміщуватись.
7) "Релейна характеристика".
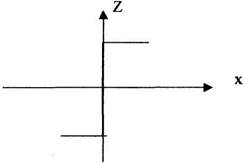
Досконале поляризоване реле.
8) "Релейна зона нечутливості".
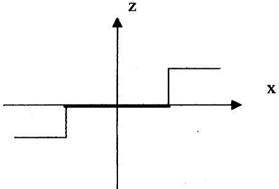
Трьохпозиційне реле з зоною нечутливості.
9) "Релейна характеристика з гістерезисом".
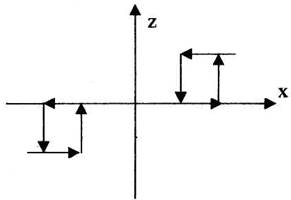
Трьохпозиційне реле з зоною нечутливості та з гістерезисом.
6.2 З’єднання нелінійних ланок
Типові нелінійні ланки і їх нормовані характеристики були введені Л.С. Гольдфарбом в 1947 році. З типовими нелінійними ланками і їх характеристиками можна оперувати подібно тому, як ми це робили з елементарними лінійними ланками.
Згадаємо типові з’єднання для лінійних ланок:
1. Послідовне.
2. Паралельне.
3. Зворотній зв’язок.
Спробуємо отримати вирази для характеристик таких же з’єднань нелінійних ланок.
1) Послідовне з’єднання.

![]()
![]() .
.
Наприклад: ![]()
![]() .
.
Між іншим, якщо для лінійних систем:
![]() ,
,
то для нелінійних систем:
![]() .
.
в загальному випадку.
2) Паралельне з’єднання.
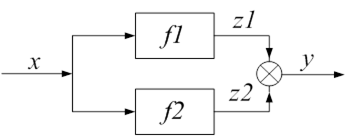
![]()
![]() .
.
Наприклад: ![]()
![]() .
.
Порівняйте з лінійними системами:
![]() .
.
3) З’єднання зі зворотнім зв’язком.
Малюємо схему з’єднання зі зворотнім зв’язком (ЗЗ).

де f1, f2 – нелінійні оператори.
Записуємо передаточну функцію для лінійної системи із ЗЗ:
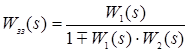 .
.
Задача
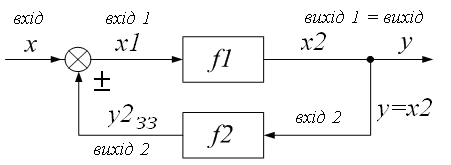
Запишемо передаточні функції (рівняння руху):
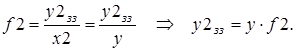
Підставимо (6.2) та (6.3) в (6.1), отримаємо:
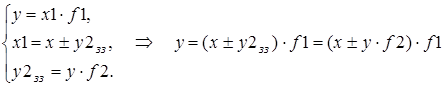 .
.Зведемо подібні в (6.4):
![]() ,
,
![]()
![]()
Тоді з (6.5) за означенням передаточної функції отримаємо передаточну функцію нелінійної системи при з’єднанні зі зворотнім зв’язком:
![]() – додатній ЗЗ;
– додатній ЗЗ;
![]() – від’ємний ЗЗ.
– від’ємний ЗЗ.
6.3 Методи фазового простору
Методи фазового простору – це сукупність кількісних і якісних, аналітичних і графічних методів аналізу і синтезу нелінійних САУ найрізноманітніших типів.
У більшості випадків нелінійна динамічна система (НДС) може бути подана у формі Коші:
де ![]() – n-мірний вектор стану;
– n-мірний вектор стану;
![]() – m-мірний вектор управління;
– m-мірний вектор управління;
![]() – p-мірний вектор збурень;
– p-мірний вектор збурень;
![]() – n-мірний вектор нелінійних функцій.
– n-мірний вектор нелінійних функцій.
Обмежимось поки розглядом НДС при ![]() та
та ![]() заданих функціях часу.
заданих функціях часу.
З теорії диференціальних рівнянь відомо, що при заданих початкових умовах ![]() та при заданих
та при заданих ![]() отримаємо деякий єдиний розв’язок рівняння (6.1). Цей розв’язок можна подати деякою траєкторією у просторі змінних
отримаємо деякий єдиний розв’язок рівняння (6.1). Цей розв’язок можна подати деякою траєкторією у просторі змінних ![]() .
.
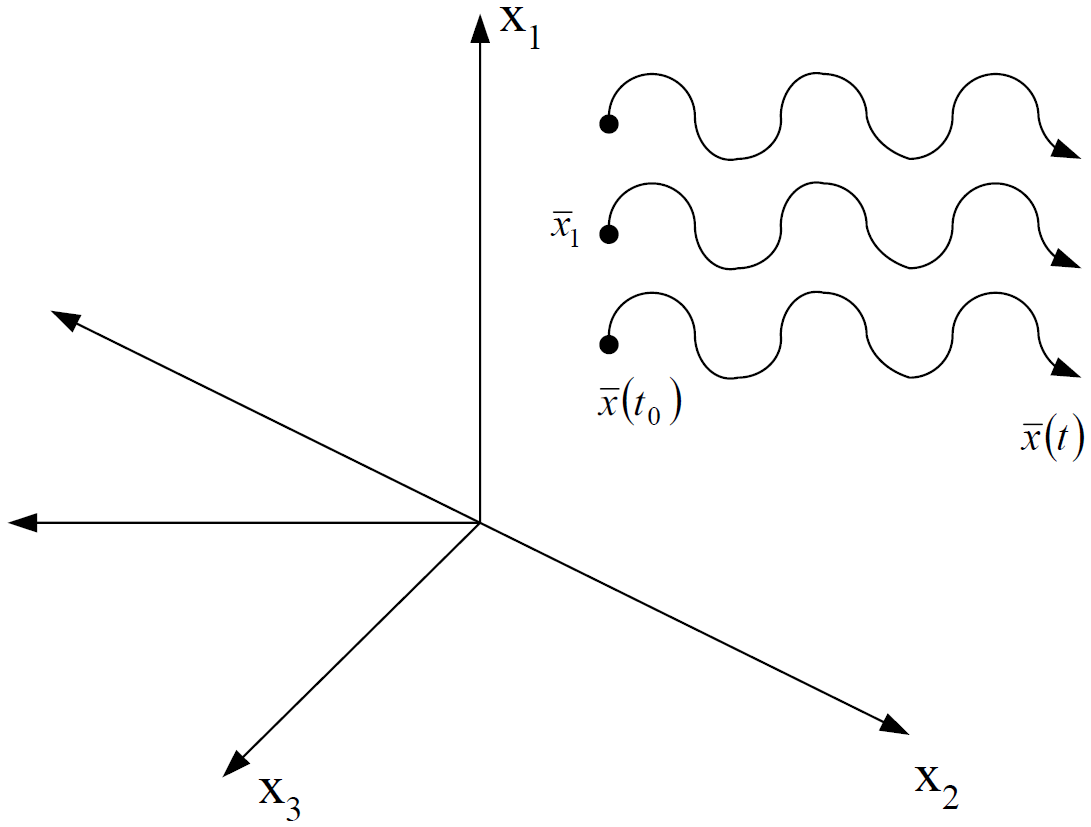 Геометричне місце таких точок дає траєкторію процесу у просторі станів.
Геометричне місце таких точок дає траєкторію процесу у просторі станів.
Якщо ![]() не залежать від часу, то можна розглядати процеси у фазовому просторі без урахування часу, тільки в аспекті зв’язку між координатами.
не залежать від часу, то можна розглядати процеси у фазовому просторі без урахування часу, тільки в аспекті зв’язку між координатами.
Для того, щоб перейти до фазових траєкторій, виключимо із системи рівнянь (1) час.
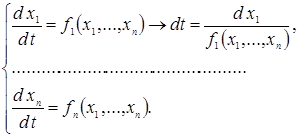
Тоді фазова траєкторія буде описуватись системою із (n-1) рівнянь:
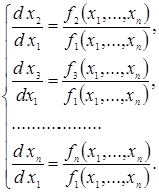
Зображення процесів у фазовому просторі знайшло найбільш широке розповсюдження для систем 2-го порядку. У цьому випадку фазовий простір зводиться до фазової площини.
Для п=2:
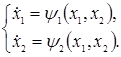
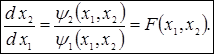
В деяких випадках можливо проінтегрувати останнє рівняння.
6.3.1 Властивості фазових траєкторій
Розглянемо деякі важливі властивості фазових траєкторій:
1) Фазові траєкторії не перетинаються якщо ![]() і
і ![]() однозначні і закінчуються при
однозначні і закінчуються при ![]() в нескінченості або в особливих точках.
в нескінченості або в особливих точках.
В окремому випадку ![]() (тобто х1 – координата, х2 – швидкість) фазові траєкторії мають наступні властивості.
(тобто х1 – координата, х2 – швидкість) фазові траєкторії мають наступні властивості.
2) В верхній напівплощині фазові траєкторії відхиляються вправо, а в нижній – вліво.
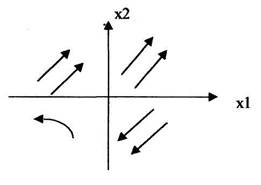
Доведення
Точка на фазовій траєкторії, що відповідає миттєвим значенням ![]() ,
, ![]() – зображуюча. З часом ця точка переміщується по фазовій траєкторії, причому напрямок її переміщення визначається тим, що час зростає, тобто
– зображуюча. З часом ця точка переміщується по фазовій траєкторії, причому напрямок її переміщення визначається тим, що час зростає, тобто ![]() .
.
Тому у верхній напівплощині, де ![]() зображуюча точка рухається зліва направо
зображуюча точка рухається зліва направо ![]() , а в нижній – справа наліво
, а в нижній – справа наліво ![]() .
.
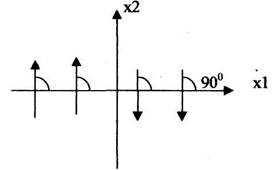
Доведення
Нехай ![]() досліджувана величина (координата),
досліджувана величина (координата), ![]() швидкість її зміни в часі. При
швидкість її зміни в часі. При ![]() отримаємо, що
отримаємо, що ![]() , тобто
, тобто
![]()
Наприклад, маємо деяке диференціальне рівняння:
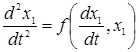 ,
,
тоді:
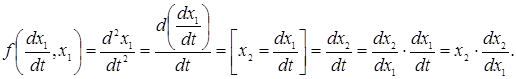
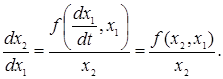
![]() .
.
При ![]() , отримаємо:
, отримаємо:
![]() .
.
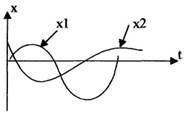
Розглянемо рівняння ![]() .
.
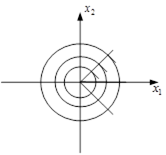
Отже, фазова траєкторія повинна перетинати ![]() (рухаючись по еліптичних траєкторіях) під кутом 900
(рухаючись по еліптичних траєкторіях) під кутом 900
Серед точок фазової траєкторії виділяють так звані особливі точки (стаціонарні, нерухомі). Особливі точки відповідають положенням рівноваги систем управління, що використовуються, так як в цих точках ![]() .
.
Ізоклиною – називається геометричне місце точок з однаковим кутом нахилу інтегральних кривих (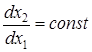 ).
).
Ізоклини полегшують побудову фазових траєкторій.
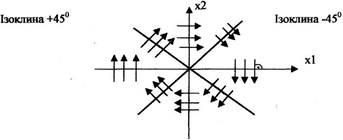
Приклад:
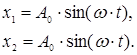
6.3.2 Класифікація особливих точок
Класифікація особливих точок представлена на рис. 6.1.
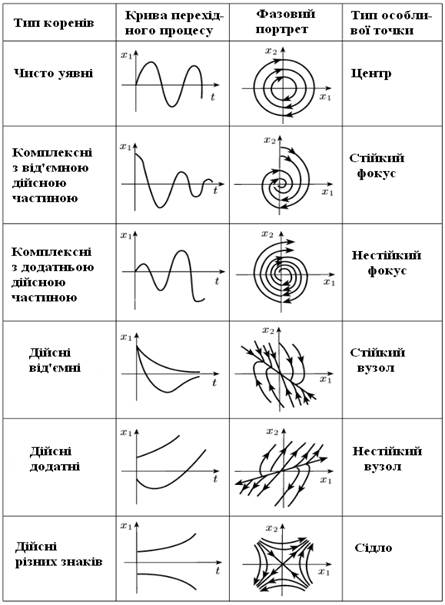
Рисунок 6.1 – Класифікація особливих точок
6.4 Стійкість нелінійних систем
У першій частині ТАУ ми отримували необхідну і достатню умову стійкості лінійних динамічних систем. Усі корені характеристичного рівняння системи повинні бути „лівими”.
Для імпульсних лінійних систем корені повинні лежати всередині одиничного кола. Для нелінійних САУ таких простих і загальних критеріїв та методів аналізу стійкості немає. Для нелінійних систем існує багато часткових методів. І один загальний – це другий метод Ляпунова. Особливість другого методу – треба кожного разу конструювати функцію Ляпунова. Перейдемо до розгляду цього методу.
Дано: динамічна система;
![]() ,
,
![]() - n-мірний вектор стану;
- n-мірний вектор стану;
![]() - n-мірна вектор-функція.
- n-мірна вектор-функція.
У загальному випадку маємо:
![]() =0.
=0.
Для такої довільної динамічної системи є справедливими дві теореми Ляпунова. Запишемо їх у канонічному формулюванні Ляпунова.
Теорема 1
Якщо існує знаковизначена функція ![]() , похідна якої по часу
, похідна якої по часу
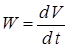 , в силу диференційних рівнянь руху є або
, в силу диференційних рівнянь руху є або
знакопостійна функція протилежного з V знаку, або ж тотожно
дорівнює 0,
то незбурений рух є стійким.
Довідка.
Знакопостійна функція: функція ![]() називається знакопостійною на множині, якщо вона приймає недодатні або невід’ємні значення і може дорівнювати нулю не лише в одній точці
називається знакопостійною на множині, якщо вона приймає недодатні або невід’ємні значення і може дорівнювати нулю не лише в одній точці ![]() . (В першому випадку функція називається від'ємно постійною, в другому – додатньо постійною).
. (В першому випадку функція називається від'ємно постійною, в другому – додатньо постійною).
Знакозмінна функція: функція ![]() називається знакозмінною на множині, якщо вона в цій області приймає як від’ємні так і додатні значення.
називається знакозмінною на множині, якщо вона в цій області приймає як від’ємні так і додатні значення.
Теорема 2.
Якщо крім того, функція ![]() знаковизначена (тобто не має нульових
знаковизначена (тобто не має нульових
точок ![]() ),
),
то незбурений рух стійкий асимптотично.
Я думаю, ви зможете за допомогою графіків та схем самостійно дати визначення знакопостійної і знаковизначеної функції.
Зрозуміти зміст функції Ляпунова можна за допомогою раніше розглянутого фазового простору.
Намалюємо фазові траєкторії і лінії постійного рівня функції Ляпунова, ![]() .
.
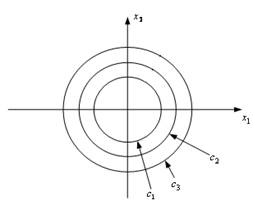

![]()
Фазові траєкторії перетинають (пронизують) цю поверхню тільки „ззовні”.
„Фізичний зміст” цієї поверхні – рівні узагальненої потенційної енергії: стійкому стану відповідає мінімум потенційної енергії; стійким процесам відповідають такі, в яких потенційна енергія зменшується (не обов’язково монотонно).
Функцію Ляпунова треба „вгадати”.
Тільки для лінійних систем її вид відомий:
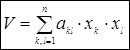 ,
,
або в векторно-матричній формі:
![]() ,
,
де А – п*п матриця шуканих коефіцієнтів функції Ляпунова.
Тоді похідну по часу від функції п-змінних – в свою чергу, функції часу – ми можемо записати у вигляді суми:
![]() .
.
Для НДС з малими нелінійностями:
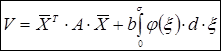 ,
,
де ![]() – зміна інтегрування,
– зміна інтегрування,
![]() – статична нелінійність класу (0, К):
– статична нелінійність класу (0, К):
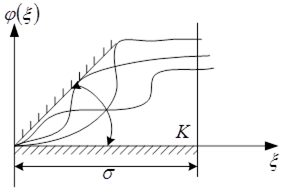
Проводимо дотичну до нелінійності з кутом К. Нелінійності, які лежать у цьому куті – нелінійності класу (0, К).
6.4.2 Абсолютна стійкість. Критерій абсолютної стійкості В. М. Попова
Розглянемо нелінійну САУ, яка складається із лінійної частини і однієї статичної нелінійності (можливо приведеної) наступного вигляду:
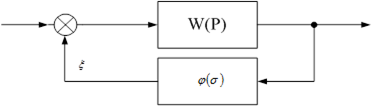
- Що таке статична нелінійність?
– Це змінний коефіцієнт зворотнього зв’язку.
Можна розглядати стійкість таких систем для цілих класів нелінійностей. Ці класи можна задати як:
− Нелінійність класу (0, К);
− Нелінійність класу (К1, К2).
У 1960 році ад’юнкт Московської академії, румунський громадянин В. М. Попов запропонував критерій стійкості таких систем. Цей критерій являє собою конкретизацію 2-го методу Ляпунова і доводиться на основі теорем Ляпунова.
Розглянемо формулювання та інтерпретації критерію Попова.
Випадок 1: Стійка лінійна частина.
Для стійкості рівноваги необхідно і достатньо щоб існувало дійсне ![]() , при якому:
, при якому:
1) ![]() (дійсна частина функції Попова), де функція Попова визначається наступним чином:
(дійсна частина функції Попова), де функція Попова визначається наступним чином:
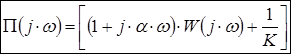 ,
,
так як
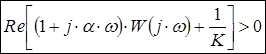
2) нелінійність належить до класу (0, К), тобто ![]() , або
, або 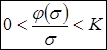 .
.
Критерій Попова рідко застосовується в алгебраїчній формі, і часто в геометричній.
Геометрична інтерпретація критерію Попова
Введемо ![]() таку, що
таку, що
![]() ,
, ![]() .
.
Нехай:
![]() .
.
Тоді згідно визначенню:
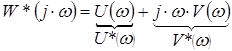 .
.
Виразимо ![]() через
через ![]() :
:
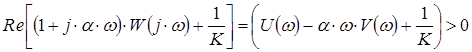 ,
,
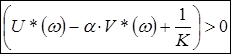 .
.
Нехай ![]() – будь-які (не належать
– будь-які (не належать ![]() точки комплексної площини, тоді граничному випадку нерівності
точки комплексної площини, тоді граничному випадку нерівності ![]() відповідає пряма з нахилом
відповідає пряма з нахилом ![]() , що проходить через точку
, що проходить через точку 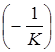 на дійсній вісі.
на дійсній вісі.
Таким чином, критерій Попова може бути сформульований наступним чином:
НСАУ зі стійкою та цілком керуємою лінійною частиною абсолютно стійка у класі статичних нелінійних характеристик (0, К), якщо через точку 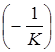 на дійсній вісі комплексної площини
на дійсній вісі комплексної площини ![]() можна провести пряму так, щоб перетворена частотна характеристика
можна провести пряму так, щоб перетворена частотна характеристика ![]() лежала б праворуч від цієї прямої.
лежала б праворуч від цієї прямої.
Геометрично розглянутий критерій виглядає так:
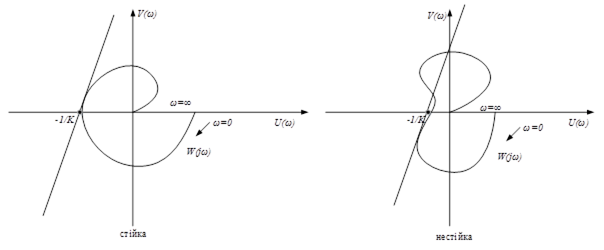
Випадок 2: Нестійка лінійна частина СРС!
Контрольні питання
1. Визначення поняття стійкості по Ляпунову.
2. Необхідна і достатня умови стійкості лінійних динамічних систем.
3. Формулювання критерія Найквиста.
4. Намалюйте, не роздумуючи, АЧХ та ФЧХ елемента запізнення
5. Визначення запасів стійкості по фазі, по амплітуді.
7. Що таке "граничне запізнення" і як його визначити?
8. Намалюйте, не роздумуючи, АФЧХ системи з граничним запізненням
9. Намалюйте на АФЧХ запаси стійкості по фазі і амплітуді.
10. Намалюйте на АЧХ та ФЧХ запаси стійкості по фазі і амплітуді.
11. Наведіть приклади з практики, де має місце запізнення.