Попередня сторінка Зміст Наступна сторінка Електронні посібники ВНТУ
7 АНАЛІЗ І СИНТЕЗ ТЕРМІНАЛЬНИХ САУ
7.1 Класифікація задач термінального управління
7.2 Постановка задачі термінального управління
7.3 Розв’язання задачі розгону
7.4 Розв’язання задачі приведення
7.5 Розв’язок задачі зближення
7.6 Структурна схема термінальної САУ
7.8 Принципи розв’язку термінального управління для багатомірного об’єкта
7.9 Структурна схема термінальної САУ
7.10 Загальні властивості управління по вищій похідній
Термінальне управління – УКС (управління кінцевим станом).
Задачі термінального управління – одне з джерел варіаційного числення, яке традиційно вважається незбагненним для більшості смертних і дається тільки в університетах.
Розглянемо один з можливих підходів до побудови простих систем термінального управління. Основа даного підходу – управління по вищій похідній.
Історія виникнення та застосування управління по вищій похідній достатньо драматична. Метод розроблений та застосовувався в реальних системах в СРСР. Монографія по цьому методу не була опублікована, оскільки його „недоліком” була простота (як вважали респонденти). Потім цей метод був запатентований в CША (Сміт, Метклаф) і застосований в системі управління вертикально злітаючим літаком „Харіер” в Англії, тоді і була вперше опублікована книга А.П. Батенко „Управление конечным состоянием объектов” на Україні.
7.1 Класифікація задач термінального управління
Розглянемо класифікацію на прикладі простої задачі управління рухом матеріальної точки по прямій. Звичайно, класифікація застосовується і для будь-яких багатомірних задач.
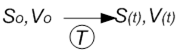
Нам потрібно об’єкт з т. А перемістити т. В за T - час переходу:
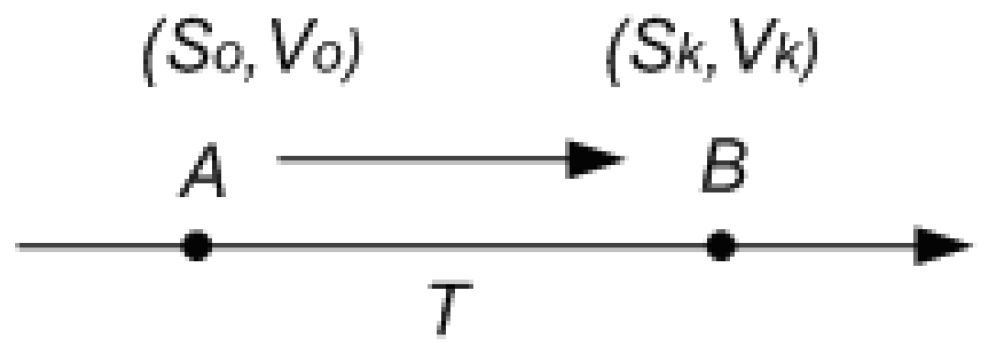
1. Задача розгону.
Умовно зображується:

Через час T потрібно отримати необхідну швидкість. Якщо T фіксується, то задача розгону замкнена, якщо T- час не фіксований, то задача розімкнена.
2. Задача приведення.
Контролюється тільки координата.
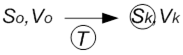
3. Задача зближення.
Зафіксували Sk, Vk.
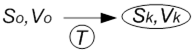
4. Задача м’якого зближення.
Uk - прискорення.

5. Задача супроводження.
Кінцеві координати змінюються по певному закону.
(Приклад: робот закручує гайку на автомобілі, який рухається по конвеєру, тобто робот супроводжує автомобіль).
6. Задача зустрічі.
Приклад: дворукий робот (рух рук); зближення космічних кораблів, коли обидва активні.

7.2 Постановка задачі термінального управління
Будемо розглядати одномірну задачу.
1) Рівняння динаміки об’єкта (рух об’єкта вздовж вісі S) розглянемо у вигляді:
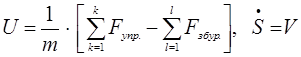
(порівняйте з законом Н’ютона: ![]() ),
),
де m – маса об’єкта;
![]() – сума проекцій на вісь S керованих сил, що викликані взаємодією керуючих органів із зовнішнім середовищем і тягою (впливом) двигунного пристрою;
– сума проекцій на вісь S керованих сил, що викликані взаємодією керуючих органів із зовнішнім середовищем і тягою (впливом) двигунного пристрою;
![]() – сума проекцій на вісь S некерованих сил, що викликані дією зовнішнього середовища.
– сума проекцій на вісь S некерованих сил, що викликані дією зовнішнього середовища.
2) Припустимо, що виконується необхідна умова керованості:
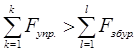 , для всіх
, для всіх ![]() період переходу.
період переходу.
3) В якості керуючого впливу вибираємо вищу похідну. В даному випадку ![]() – прискорення. В цьому і полягає основна суть запатентованого методу управління по вищій похідній.
– прискорення. В цьому і полягає основна суть запатентованого методу управління по вищій похідній.
4) Управління шукаємо у вигляді полінома від ![]()
![]()
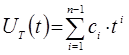 ,
,
де ![]() – необхідне управління;
– необхідне управління;
![]() – кількість граничних умов;
– кількість граничних умов;
![]() – шуканий коефіцієнт.
– шуканий коефіцієнт.
Наприклад, для ![]()
![]()
![]()
Кількість доданків в ![]() беремо рівною кількості граничних умов для того, щоб отримати єдиний розв’язок.
беремо рівною кількості граничних умов для того, щоб отримати єдиний розв’язок.
1) Припустимо, що керуючий вплив – прискорення, створюється за
допомогою достатньо точної і швидкодіючої слідкуючої системи так, що
![]()
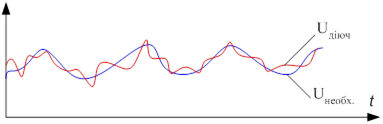
![]()
Щоб виконувалась рівність,
необхідно, щоб система була слідкуючою.
7.3 Розв’язання задачі розгону
Нехай початкова швидкість об’єкту ![]() . Необхідно за час T розігнати його до швидкості
. Необхідно за час T розігнати його до швидкості ![]() :
:

1. При одній граничній умові ![]() управління набуде виду:
управління набуде виду:
![]() .
.
2. Інтегруємо рівняння руху:
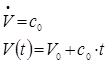
Рівняння для S не знадобиться.
3. Підставляємо t=T
![]() .
.
За означенням, ![]() звідки бачимо, що
звідки бачимо, що
Це кінцевий результат в першому наближенні. Таким чином, вирішили задачу розгону:
Постійне прискорення, яке будучи прикладеним до об’єкту, за час T розгонить його до швидкості ![]() .
.
Однак такий спосіб управління є програмним ![]() розімкненим по управляючій фазовій координаті
розімкненим по управляючій фазовій координаті ![]() , він не враховує помилок, які з’являються в процесі. Необхідний обернений зв’язок
, він не враховує помилок, які з’являються в процесі. Необхідний обернений зв’язок ![]() . Таким чином, вирішивши проблему термінального управління – ми створили нову проблему – проблему введення зворотнього зв’язку.
. Таким чином, вирішивши проблему термінального управління – ми створили нову проблему – проблему введення зворотнього зв’язку.
4. Введення зворотнього зв’язку.
Будемо вважати поточний фазовий стан об’єкта початковим, тому в (7.4) ![]() замінимо на поточну швидкість
замінимо на поточну швидкість ![]() , а заданий час розгону
, а заданий час розгону ![]() – на залишившийся час
– на залишившийся час ![]() , де
, де ![]() відліковується з моменту початку розгону. Отримаємо закон управління з оберненим зв’язком:
відліковується з моменту початку розгону. Отримаємо закон управління з оберненим зв’язком:
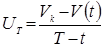
Закон управління з оберненим зв’язком (7.5) володіє особливістю в кінцевій точці ![]() В кінцевий момент
В кінцевий момент ![]() – помилка кінцевого стану. Управління, необхідні для виправлення помилки, зростають з часом. При
– помилка кінцевого стану. Управління, необхідні для виправлення помилки, зростають з часом. При ![]() . Таким чином, виникає чергова проблема – проблема усунення особливості.
. Таким чином, виникає чергова проблема – проблема усунення особливості.
Що ж це виходить – вирішили проблему, а виникла інша, це випадковість чи закономірність?
Давайте познайомимося із загальними закономірностями.
4.1 Методологія рішення проблем (МРП).
Можливі три шляхи позбавлення від проблеми:
1) Ліквідування проблеми – зняття проблемної ситуації шляхом зміни початкового цілеспрямування, тобто зміни початкової мети.
2) Розв’язання проблеми – ліквідування проблемної ситуації шляхом використання однієї з можливих альтернатив впливів.
3) Вирішення проблеми – вибір з набору припустимих альтернатив впливів тієї, яка приводить до оптимального або до бажаного стану.
Рішення проблеми вимагає знання:
а) набору припустимих альтернатив – рішень;
б) оцінки наслідків їх прийняття;
в) класифікації і (або) упорядкування припустимих альтернатив на підмножини не задовільних і задовільних.
При формуванні та рішенні важливих проблем корисно знати їх загальні закономірності, зокрема, закони ”методології рішення проблеми” (МРП) Е. Шейля:
1-й закон МРП: будь – який розв’язок проблеми створює ще одну нову, що призводить до лавиноподібного росту кількості проблем і викликає бажання взагалі їх не розв’язувати.
2-й закон МРП: будь – який не розв’язок призводить до того, що розв’язок буде знаходитись спонтанно, тобто стихійно (випадково).
3-й закон МРП: за сумою проблем, як правило, існує одна велика, центральна проблема, а всі інші проблеми є тільки симптомами цієї центральної проблеми.
Наслідок 1. Лише системний підхід дозволяє за окремими проблемами побачити центральну.
Наслідок 2. Виявлення центральної проблеми та пошук її розв’язку – оптимальний шлях в методиці розв’язку проблем.
Повернемося до розв’язку проблеми ліквідування особливості.
5. Ліквідація особливості.
Альтернативи усунення особливості.
Розглянемо наступні альтернативи усунення особливості:
5.1. Якщо вимоги до точності управління не дуже жорсткі, то можна вважати розгін виконаним, не доходячи до кінцевої точки інтервалу ![]() на малу величину
на малу величину ![]() . Помилка розгону при цьому буде дорівнювати:
. Помилка розгону при цьому буде дорівнювати:
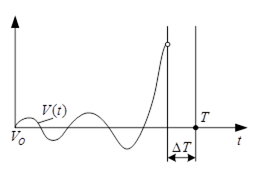
Відключення системи управління, тобто ![]() для будь-якого t,
для будь-якого t,
де ![]() .
.
5.2. При другому способі інтервал ![]() необхідно розбити на дві нерівних ділянки:
необхідно розбити на дві нерівних ділянки: ![]() і
і ![]() . На більшій з них
. На більшій з них ![]() слід використати закон управління (5) зі зворотнім зв’язком. На заключній, короткій ділянці
слід використати закон управління (5) зі зворотнім зв’язком. На заключній, короткій ділянці ![]() застосовується програмне управління (4). Практично це робиться так. В момент часу
застосовується програмне управління (4). Практично це робиться так. В момент часу ![]() задане прискорення фіксується і в подальшому підтримується незмінним впродовж залишкового часу руху
задане прискорення фіксується і в подальшому підтримується незмінним впродовж залишкового часу руху ![]() .
.
![]() , для будь-якого T, де
, для будь-якого T, де ![]() – фіксація управління, починаючи з деякого моменту
– фіксація управління, починаючи з деякого моменту ![]() .
.
5.3. В третьому способі кінцева фазова точка, яка задається в якості мети управління в законі (5), виноситься за межі ділянки ![]() на величину
на величину ![]() секунд і розташовується на продовженні фазової траєкторії, яка з’єднує точки
секунд і розташовується на продовженні фазової траєкторії, яка з’єднує точки ![]() і
і ![]() . Ця винесена точка
. Ця винесена точка ![]() відноситься до моменту часу
відноситься до моменту часу ![]() . Об’єкт, рухаючись до неї, при
. Об’єкт, рухаючись до неї, при ![]() пройде через точку
пройде через точку ![]() , яка є метою управління.
, яка є метою управління.
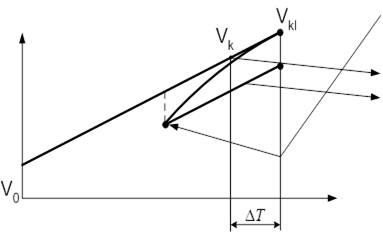
1. Нехай по якій-небудь причині виникла помилка.
2. Виправленняпомилки із ЗЗ.
3. Рух об’єкту з прискоренням по програмному режиму.
В четвертому способі кінцева точка ![]() не виноситься за межі ділянки
не виноситься за межі ділянки ![]() , а робиться рухомою і розташовується попереду зображуючої фазової точки об’єкту на часовому інтервалі
, а робиться рухомою і розташовується попереду зображуючої фазової точки об’єкту на часовому інтервалі ![]() . Таким чином, реалізується погоня об’єкту за рухомою фазовою точкою. (Приклад: змагання собак (тікаючий заєць); керування конем без вожжей).
. Таким чином, реалізується погоня об’єкту за рухомою фазовою точкою. (Приклад: змагання собак (тікаючий заєць); керування конем без вожжей).
Нехай необхідно перевести об’єкт зі стану ![]() в стан
в стан ![]() . За формулою (10.4) обчислимо задане на ділянці
. За формулою (10.4) обчислимо задане на ділянці ![]() прискорення і використаємо його для обчислення заданої програми руху, тобто поточної швидкості ведучої точки С на ділянці
прискорення і використаємо його для обчислення заданої програми руху, тобто поточної швидкості ведучої точки С на ділянці ![]() .
.
Закон управління (5) прийме форму:
![]() – жорсткість управління.
– жорсткість управління.
Підставимо в (7) вираз для ![]() (6), приводимо закон управління (5) до виду:
(6), приводимо закон управління (5) до виду:
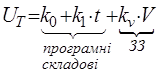
Від звичайного закону управління термінальне управління відрізняється наявністю програмних складових
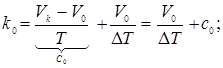
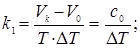
![]() .
.
(“–“ зворотній від’ємний зв’язок).
Точка, яку ведуть (ведома) повторює рух точки, що веде (ведуча) з запізнюванням по часу на ![]() секунд.
секунд.
Чим менше ![]() , тим швидше виходить об’єкт на задану фазову траєкторію (
, тим швидше виходить об’єкт на задану фазову траєкторію (![]() – величина часового інтервалу між точками – жорсткість управління).
– величина часового інтервалу між точками – жорсткість управління).
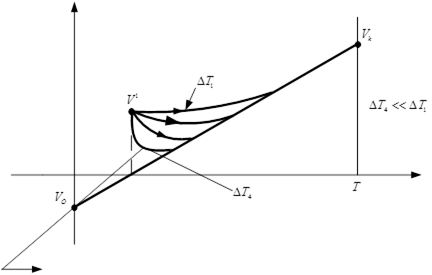
Рисунок 7.1 – Аналіз жорсткості управління
![]() – фазова траєкторія руху об’єкта;
– фазова траєкторія руху об’єкта;
![]() – виникла помилка (відхилення координат від заданої траєкторії); чим менше жорсткість управління
– виникла помилка (відхилення координат від заданої траєкторії); чим менше жорсткість управління ![]() , тим швидше повертається об’єкт на задану траєкторію, але при цьому необхідно прикласти більше прискорення;
, тим швидше повертається об’єкт на задану траєкторію, але при цьому необхідно прикласти більше прискорення;
![]() – слід вибирати так, щоб
– слід вибирати так, щоб ![]() .
.
7.4 Розв’язання задачі приведення
Будемо слідувати порядку роз’язання задачі розгону! ![]()
Задача приведення:
![]()
Необхідно привести об’єкт в точку з координатою ![]() в момент часу
в момент часу ![]() . На кінцеву швидкість умов не накладається:
. На кінцеву швидкість умов не накладається:
1. Кількість граничних умов:
2. Інтегруємо рівняння руху:
![]()
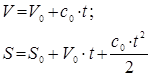
3. Підставляємо ![]()
![]()
вираз для ![]() (необхідне прискорення).
(необхідне прискорення).
4. Введення зворотнього зв’язку.
Робимо заміну:
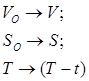
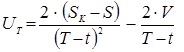
закон управління з урахуванням зворотнього зв’язку.
5. Ліквідуємо особливість.
Робимо заміну:
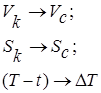
де
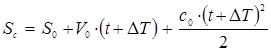
Після алгебраїчних перетворень отримуємо
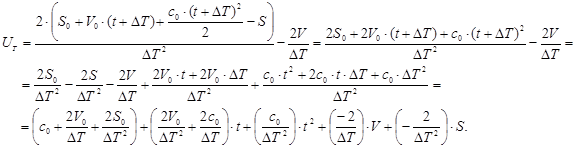
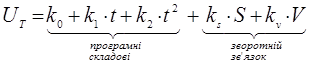
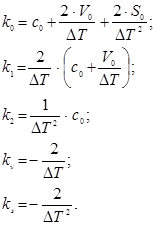
7.5 Розв’язок задачі зближення
В задачі розгону ми навчилися керувати швидкістю об’єкта, а в задачі приведення – координатою. Однак, в техніці часто вимагається, щоб швидкість і координата одночасно прийняли б задані значення. В який момент часу це станеться, іноді не так важливо, іншими словами, час може бути некерованим параметром. Ми домовилися називати САУ, побудовані по такому принципу, розімкненими по часу. Можна назвати цілий ряд об’єктів, яким необхідні такі САУ: вертольоти, літаки вертикального взльоту та посадки (ЛВВП), космічні літальні апарати (КЛА), поїзди метрополітену і т.п. Літальні апарати повинні проводити м’яку посадку, отже, при дотику до поверхні їх кінцева швидкість повинна стати нульовою. Поїзди метрополітену повинні гальмувати так, щоб зупинятися точно біля платформи.
Однак, в деяких задачах цього не достатньо. Наприклад, в системі управління повітряним рухом необхідно, щоб літаки прибували в призначену точку повітряного простору (початок взлітно-посадочної полоси) з заданою посадковою швидкістю у визначений час. Одночасний вихід двох об’єктів в призначену точку простору для стиковки або дозаправки також потребує, щоб керуванню піддавались координата, швидкість, час.
Задача зближення:
![]()
1) Кількість граничних умов: ![]()
Закон управління буде мати два невідомих параметра:
2) Інтегруємо рівняння руху:
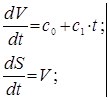
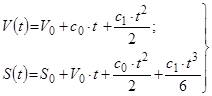
3) Підставляємо ![]() в (2):
в (2):
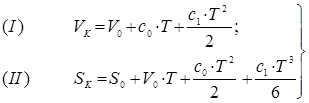
Розв’яжемо систему рівнянь (10.17) відносно двох невідомих ![]() і
і ![]() :
:
![]()
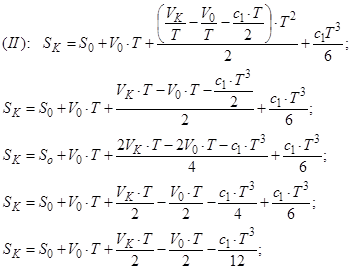
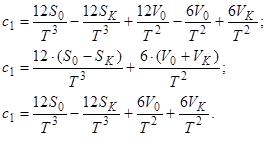
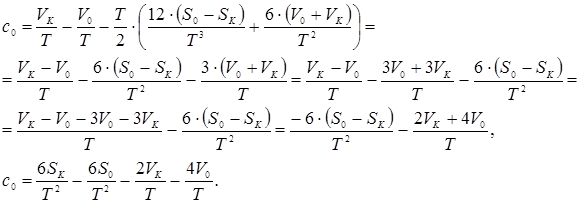
Отримали вирази для ![]() і
і ![]() :
:
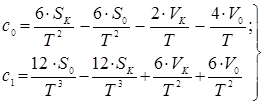
4) Введемо зворотній зв’язок.
Робимо заміну:
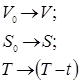
Відлік часу при зближенні проводиться з моменту виходу об’єкту з початкової точки. Так, як об’єкт тепер весь час знаходиться в початковій точці, то ![]() і другий член в формулі для прискорення (1) зникне:
і другий член в формулі для прискорення (1) зникне:
![]() .
.
При цьому закон управління (1) прийме вигляд:
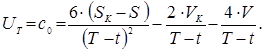
5) Ліквідування особливості.
Розглянемо метод фазової точки:
Робимо заміну:
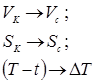
Підставляємо замість ![]() , отримаємо поточні фазові координати ведучої точки:
, отримаємо поточні фазові координати ведучої точки:
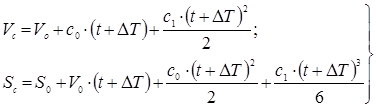
Після деяких дій з підстановками отримаємо:
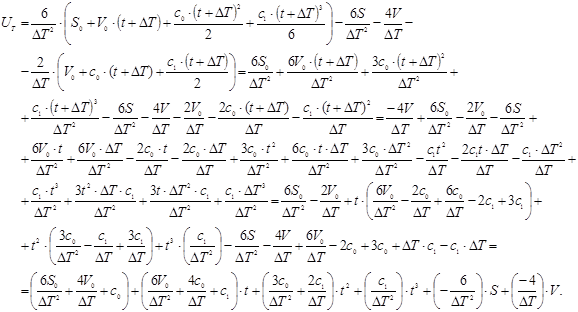
де
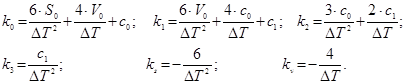
Вибором ![]() регулюється „жорсткість” прив’язки керуємого об’єкту до програмної фазової траєкторії.
регулюється „жорсткість” прив’язки керуємого об’єкту до програмної фазової траєкторії.
7.6 Структурна схема термінальної САУ
(для задачі зближення)
![]()
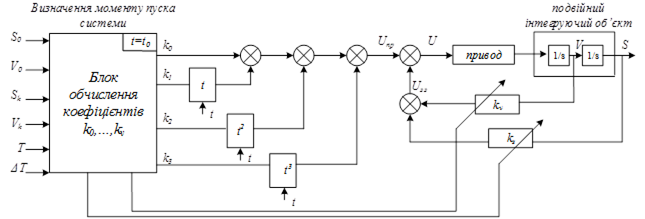
Рисунок 7.2 – Структурна схема термінальної САУ
![]() – змінні коефіцієнти, які встановлюються кожен раз у відповідності до необхідної задачі.
– змінні коефіцієнти, які встановлюються кожен раз у відповідності до необхідної задачі.
7.7 Термінальне управління при застосуванні декількох паралельно працюючих виконавчих елементів (приводів)
Для сучасних об’єктів управління характерна надлишковість виконавчих пристроїв (приводів). Причини цієї надлишковості різноманітні: вимоги надійності та живучості, багаторежимність (коли для кожного режиму використовуються різні типи виконавчих пристроїв), неможливість повного розділення каналів. В САУ таких об’єктів виникає задача забезпечення паралельної роботи декількох виконавчих пристроїв.
1) Вертикально взлітаючий літак
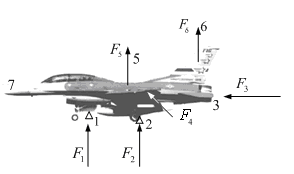
1, 2, 3 – газотурбінні двигуни;
4, 5 – аеродинамічне кермо;
6, 7 – газоструйне кермо.
Для керування рухом такого літака використовуються спільно: газотурбінні двигуни, газоструйні та аеродинамічні рулі. Надлишковість тут необхідна, як для надійності, так і для забезпечення працездатності на різних режимах (аеродинамічне кермо неефективне на малих швидкостях). Необхідно, щоб на всіх режимах – посадка, розгін, ... – ці виконавчі органи працювали узгоджено.
2) Роботи–маніпулятори по багатьом причинам вимушені копіювати, наприклад, людську руку.
Розглянемо типову схему РМ (робота-маніпулятора).
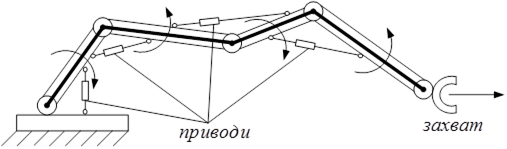
Рисунок 7.3 – Типова схема робота-маніпулятора
Більшість РМ являють собою кінематичний ланцюг (поки з 2-3 ланцюгів, в майбутньому із 3-10).
Вочевидь, рух захвату складним нелінійним чином залежить від обертальних рухів окремих ланцюгів.
Як керувати окремими ланцюгами, щоб їх рухи склались в цілеспрямований стійкий рух захвату?
Традиційними методами ТАУ таку задачу при кількості ланцюгів більше трьох розв’язати неможливо. Як же узгодити окремі приводи РМ ?
З’ясували, що термінальне управління по вищій похідній дозволяє включати на паралельну роботу необмежену кількість виконавчих пристроїв. Причому, термінальна САУ виявляється нечутливою до нелінійності окремих виконавчих пристроїв і навіть до відмов.
Як це довести? В даному випадку при довільних нелінійностях для доведення може використовуватися моделювання перехідних процесів в системі, хоча можливо застосовувати і деякі аналітичні методи (метод функцій Ляпунова, ...), однак тільки для вузьких класів нелінійностей.
Таким чином, для доведення використовується експеримент – модельний або натуральний.
Розглянемо схему термінальної САУ з паралельними виконавчими органами.
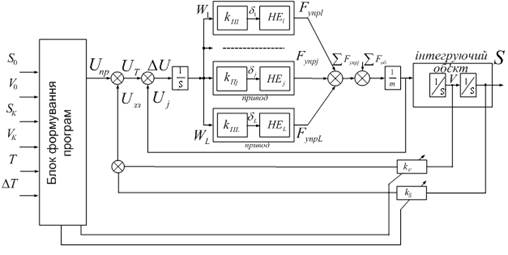
Рисунок 7.4 – Схема термінальної САУ з паралельними виконавчими органами
![]() – коефіцієнт передачі (підсилення) окремого привода, що обирається в широких межах;
– коефіцієнт передачі (підсилення) окремого привода, що обирається в широких межах;
![]() – структурний елемент, який характеризує нелінійності привода.
– структурний елемент, який характеризує нелінійності привода.
В якості управляючого впливу (однакового для всіх приводів) використовується ![]() :
:
![]()
що в підсумку забезпечує астатизм внутрішнього контуру ![]()
При використанні метода управління по вищій похідній не вимагається здійснювати узгодження паралельно працюючих виконавчих елементів. Достатньо подати на всі елементи один і той же управляючий вплив ![]() .
.
7.8 Принципи розв’язку термінального управління для багатомірного об’єкта
Ми досліджували модель руху об’єкту, яка складається з двох інтегруючих ланок. Звичайно, що ця модель справедлива, якщо час обробки заданого прискорення (сили) достатньо малий, щоб ним можна було знехтувати. Якщо ж врахувати динамічні властивості САУ та силової установки, то модель руху об’єкту буде багатомірною. Однак до неї можуть застосовуватися підхід та методика дослідження, розглянуті раніше.
Передаточна функція багатомірного об'єкту (лінійного):
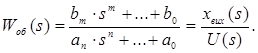
Диференційне рівняння має вигляд:
![]() .
.
В якості управляючої функції візьмемо вищу похідну вихідної величини, нехай ![]() :
:
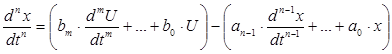
Побудуємо структурну схему для моделювання об’єкта.
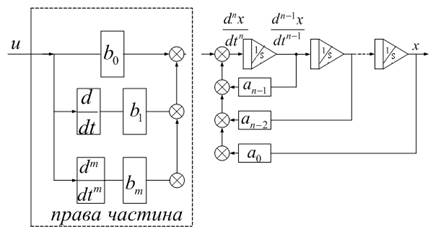
Рисунок 7.5 – Структурна схема для моделювання об’єкта
Моделлю об’єкту є ланцюг з послідовно ввімкнених інтеграторів з від’ємними зворотними зв’язками, які замикаються на її вхід. Довжина ланцюга визначається порядком характеристичного полінома.
Отже, в основі моделі будь-якої лінійної системи лежить ланцюг інтеграторів. Дослідимо властивості цього ланцюга.
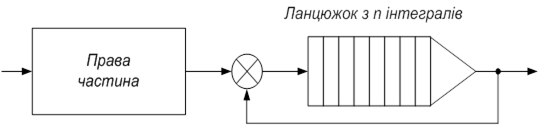
Рисунок 7.6 – Ланцюг інтеграторів
![]()
Застосуємо методику синтезу термінального управління зі зворотнім зв’язком.
Позначимо:
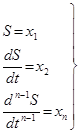
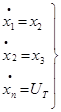
(Не плутати S – координату та s – змінну характеристичного полінома !).
Нехай на ![]() перших фазових координат накладені обмеження:
перших фазових координат накладені обмеження:
![]() .
.
Управління шукаємо у вигляді:
![]() .
.
Підставляємо ![]() в
в ![]() диференційне рівняння об’єкта, послідовно їх інтегруємо, підставивши
диференційне рівняння об’єкта, послідовно їх інтегруємо, підставивши ![]() :
:
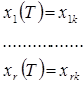
Отримаємо систему алгебраїчних рівнянь для коефіцієнтів ![]() .
.
Вводимо зворотній зв’язок і ліквідуємо особливість.
Зробимо заміну:
ЗЗ ![]()
Усун. особл. ![]() ,
,
де
![]() .
.
Кінцевий вигляд ![]() :
:
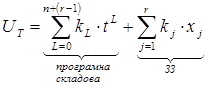
7.9 Структурна схема термінальної САУ
Структурна схема термінальної САУ для об’єкта-ланцюга інтеграторів представлена на рисунку 7.7.
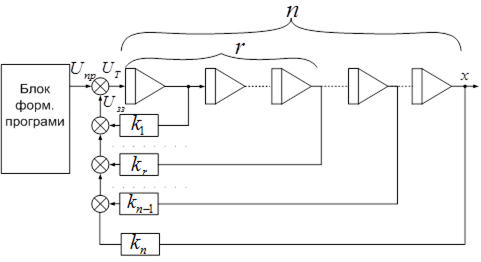
Рисунок 7.7 – Структурна схема термінальної САУ для об’єкта-ланцюга інтеграторів
7.10 Загальні властивості управління по вищій похідній
1)Близько 95% задач термінального управління описуються за допомогою математичної моделі 2-го порядку.
2)Динаміка об’єкту мало відбивається на кінцевій точності САУ.
3)Нелінійності в системі і обмеження, накладання на переміщення управляючих органів, практично не відбиваються на кінцевій точності управління.
4)На паралельну роботу можна включити скільки завгодно різних виконавчих елементів без будь-якого попереднього узгодження їх між собою.
5)Структура САУ визначається не динамікою об’єкту, а характером задачі, яка виконується.
6)Передаточні числа виконавчих елементів можуть вибиратися довільно, достатньо в широкому діапазоні значень.
7)Для реалізації термінального управління необхідний зворотній зв’язок по всім фазовим координатам, які контролюються, тобто фактично управління по вектору стану. Але ми вже знаємо, що в практичних задачах вектор стану повністю невимірюваний. Таким чином, спостерігач необхідний і при розв’язку задачі термінального управління.
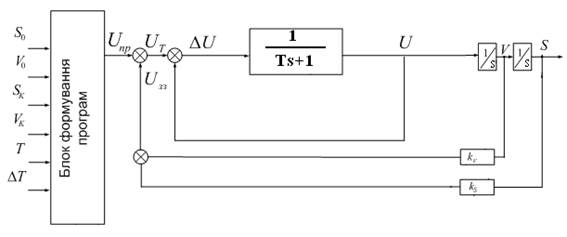
Рисунок 7.8 – Структурна схема термінального управління
I спосіб:

Підставимо (2) в (1):
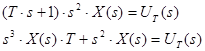
Виконаємо обернене перетворення Лапласа і приведемо коефіцієнт при вищій похідній до одиниці діленням на Т:
![]()
Нехай:
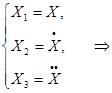
![]()
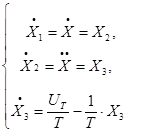
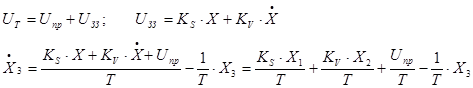
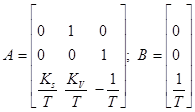 .
.
II спосіб:
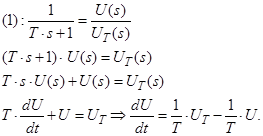

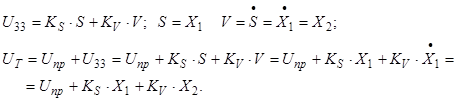
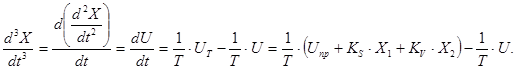
Нехай:
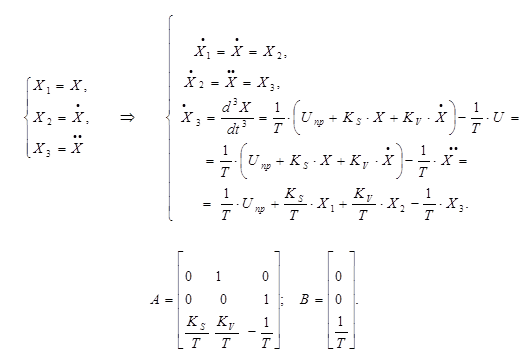
Контрольні питання:
1. Спробуйте аналітично дослідити стійкість такої САУ для типових нелінійностей (обмеження, зона нечутливості).
2. Як побудувати програму обчислювального експерименту для дослідження стійкості такої САУ ?
3. Дайте словесну формулу тривалості перехідного процеса.
4. Наведіть приклади обєктів управління, де обмежується перерегулювання.
5. Наведіть приклади обєктів управління, де обмежується прискорення.
6. Напишіть формули для обчислення всіх використаних критеріїв.