—  це залежить від того, що ви маєте в своєму розпорядженні (з чого вибирати, які строки підготовки);

—  це залежить від погоди та пори року.

Що є найбільш характерним для задач управління об'єктами будь-якої природи? Кожний одразу і без вагань здогадається: обмеження на ресурси управління. У системі управління літака — це обмеження потужності двигуна, кутів відхилення аеродинамічних органів управління, в техніко-економічній системі — це обмеження  виробничих потужностей, фінансових ресурсів, кадрів.

Який критерій оптимізації є найбільш характерним для задач управління? Знову ж таки, кожен скаже: швидкодія (зрозуміло, при обмеженнях на економічність, безпечність). Особливо у бізнесі: "другий повинен бути в десять разів кращий за першого", що в перекладі означає — запізнення з виходом на ринок з певним товаром суттєво знижує, або взагалі елімінує доходи.    

А тепер спробуйте, спираючись на власні знання, досвід та інтуїцію здогадатися, яку структуру має оптимальне за швидкодією управління при обмеженнях на управління? Або простіше, — сформулюйте принцип такого управління? Інженери, практики винайшли і застосовували цей принцип ще до того, як була створена математична теорія оптимального управління. Це так званий принцип "максимальний розгін — максимальне гальмування". Суть його в тому, що оптимальне за швидкодією управління повинно бути в кожен момент часу максимально можливим.

Вибирається  тільки напрямок  дії. Функція  оптимального  управління    звичайно має розриви — "переключення". Для таких задач важко застосувати методи класичного варіаційного обчислення — вони (методи, а не задачі) вимагають існування відповідних похідних. Саме для таких задач колективом вчених під керівництвом академіка Л. Понтрягіна на початку  1950-их  років був розроблений метод під назвою принцип максимуму.

А тепер, враховуючи, що:

а) практики і без теоретиків винайшли  структуру оптимального за швидкодією управління;

б) в сучасному світі глобалізованої, високотехнологічної, пов'язаної мережами економіки  головним  правилом є  "не займайся оптимізацією,  лови можливості !" (бестселер Стівена Келлі — "Нові правила для нової економіки. Десять радикальних стратегій для конектизованого світу").

8.1.1 Постановка задачі оптимізації

Дано:

Об'єкт управління:

.

Обмеження:

—  інтегральні:

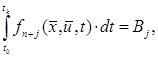
—  алгебраїчні:

       ,           

Граничні умови (можуть бути і більш складніші):

.

Критерій (показник оптимізації або цільова функція):

.

Мета оптимізації (найчастіше):

 або .

Збурення (задаються різним чином).

Необхідно знайти , при якому критерій приймає мінімальне (або максимальне) значення при заданих рівнянні об'єкта управління та обмеженнях і граничних умовах.

8.1.2 Класифікація критеріїв оптимізації

Локальні критерії:

Інтегральні критерії:

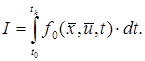
Окремі випадки інтегрального критерію:

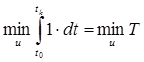 — критерій швидкодії.

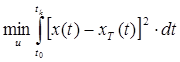— критерій інтегральної середньоквадратичної похибки.

У загальному вигляді з використанням векторно-матричної квадратичної форми цей критерій запишеться:

.

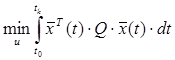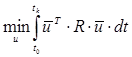 — критерій мінімуму витрат енергії на управління.

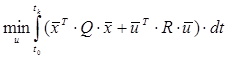— критерій,  що  об'єднує мінімум помилок та мінімум витрат енергії на управління.

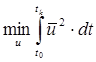 — витрати енергії на управління.

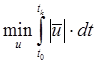 — критерій мінімуму витрат робочого тіла на управління.

8.1.3 Методи оптимізації

В даний час все різноманіття методів оптимізації може бути зведено до наступних груп методів:

1.  Методи класичного варіаційного числення. Методи варіаційного числення з'явились 100-200 років назад (Ейлер, Лагранж) з інтелектуальних математичних міркувань.

2.  Метод динамічного програмування Беллмана. У 1940-1945 рр. інженерна практика САУ вимагала методів оптимізації. У 1948 р. був створений метод Белмана.

3.  Метод принципу максимуму Понтрягіна.

8.1.4 Синтез оптимального за швидкодією управління

Для розуміння даного розділу розв’яжемо задачу. Розглядаємо об'єкт другого порядку з одним (скалярним) управлінням. Використовуємо відповідні інформаційні технології: копіюємо і редагуємо "порядок розв'язання задачі".

Дано:   

Критерій:

.

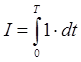Диференціальне рівняння процесу:

.

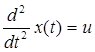Обмеження на управління (нормоване):        

.

Записуємо розширену систему рівнянь динаміки процесу: 

;      ;     .

Рівняння 2 і 3 отримані приведенням до форми Коші вхідного диф. рівняння.

Записуємо гамільтоніан (символьний процесор не працює з індексованими змінними, тому замінюємо на прості:   на   і т.д.):

;    .

Аналізуємо умови, за яких функція  досягає максимуму, тому очевидно, що:

а) тільки остання складова залежить від управління;

б) для максимізації цієї складової треба, щоб управління   мало:

б1) той самий знак, що і ;

б2) максимально можливий модуль.

Таким чином, управління буде релейним. тобто таким,  що у певні моменти змінює знак і  має граничні за модулем значення.

Записуємо і розв'язуємо рівняння для спряжених функцій (подаємо схему отримання цих рівнянь).

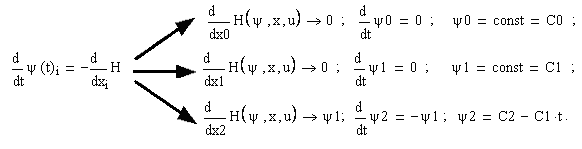
8.2 Система оптимального управління синтезом стиролу

Опис об’єкта управління. Аналіз альтернатив управління

Стирол – сировина для великотоннажної пластмаси – полістиролу. Виробництво стиролу звичайно є масовим. Реактори для синтезу стиролу працюють разом, паралельно. Причини цього – велика потреба в продукті, старіння реакторів, періодична зупинка їх для заміни каталізатора при умові підтримки заданого рівня випуску продукції. Паралельна робота реакторів, великі вимоги до надійності функціонування виробництва в цілому обумовлюють і методи управління – групового, одразу всіма реакторами.

Перша ціль управління – підтримка потрібного рівня сумарного виробництва незалежно від стану окремих реакторів. Специфіка масового виробництва продуктів у реакторах у тому, що навіть малі частки відсотка зміни експлуатаційних витрат призводять до великих сумарних економічних ефектів. З цієї причини режими роботи реакторів – тиск, температуру, концентрації – ретельно оптимізують. Характеристики реакторів з часом погіршуються – проходить процес "отруєння каталізатору". Звичайно в батареї реакторів паралельно працюють реактори, які мають різні ефективності (одиниць продукції на одиницю експлуатаційних витрат). Зрозуміло, що кращі реактори треба завантажувати більше.

Друга ціль управління – таке розподілення навантаження по реакторах, яке дає мінімум експлуатаційних витрат при заданому рівні випуску продукції. Розглянемо стисло технологічний процес синтезу стиролу (рис. 1).     

У реакторі нагрівається етилбензол в присутності каталізатора, утворюється суміш стиролу, етилбензолу, бензолу, толуолу, що переганяється, і виділений етилбензол знову йде у реактор. Реактор підігрівається парою. Особливості системи – нелінійні і нестаціонарні характеристики реактора, а також паралельна робота декількох реакторів на потрібний сумарний вихід стиролу. Необхідно розробити систему оптимального управління розподілом етилбензолу по окремих реакторах з урахуванням обмеження на сумарну продуктивність. Критерій – сумарні виробничі витрати на заданий випуск продукту. На рисунку 8.1 наведено спрощену схему системи та модель процесу синтезу стиролу.

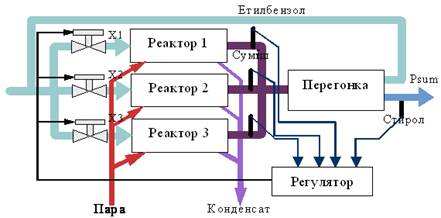
Рисунок 8.1 – Спрощена схема системи та модель процесу синтезу стиролу

Реактор для синтезу стиролу – не ракета, – він значно складніший. Щоб побудувати його аналітичну модель, треба враховувати закони каталітичної хімії, термодинаміки, газодинаміки і багато іншого. Для цілей практики іноді буває достатньо зняти експериментально характеристики реактора, а потім виконати апроксимацію цих характеристик, наприклад, поліномами.

Розробка системи оптимального управління синтезом стиролу

Математична модель реактора для аспекту "залежність виробничих витрат від виходу стиролу" – апроксимація реальної характеристики поліномом. Запишемо похідну від цієї залежності (рис.15 3).

 

(8.1)

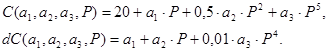
Математична модель реактора для аспекту "залежність виходу стиролу від рівня подачі етилбензолу" розглядається на рисунку 15.4. Ця характеристика є оптимізованою за іншими вхідними змінними – витратою пари, температурою, тиском та іншими. Використовуємо як перше наближення модель з одним параметром b₁. Реактори мають характеристики одного класу і відрізняються параметром b₁. Модель нереалістична для малих значень х.

 

(8.2)

Задаємо ранжовані змінні  та  і будуємо графіки характеристик.

.

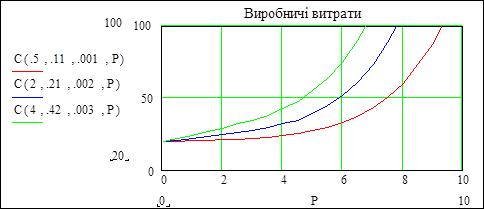
Рисунок 8.2 – Залежність виробничих витрат від виходу стиролу

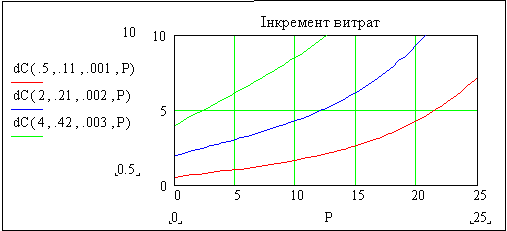
Рисунок 8.3 – Залежність інкременту виробничих витрат від виходу стиролу

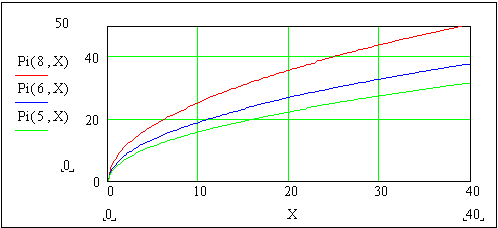
Рисунок 8.4 – Залежність виходу стиролу від виробничих витрат

Формулювання оптимізаційної задачі

Задана цільова функція – сумарні виробничі витрати.

Ціль оптимізації – мінімум цієї функції.

 

.

(8.3)

Знайти:   

 

.

(8.4)

Задано обмеження на сумарний вихід стиролу, тобто: 

 

(8.5)

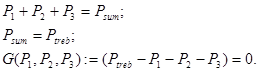
Задано: 

1)   такт квантування ;

2)   вимоги до перехідного процесу:

– тривалість 5–15 тактів квантування;

 – перерегулювання <10%;

 – точність регулювання – 5%.

Ставимо задачі першого рівня:

1. Побудувати структурну схему  управління реакторами.Обгрунтувати вибір методу синтезу і критерію оптимальності  САУ.

2.Розробити програму для знаходження оптимального розподілу навантаження реакторів методом невизначених множників Лагранжа. Визначити оптимальний розподіл і параметри регулятора.

3. Розробити математичну модель і програму моделювання АСУТП.     

4. Виконати моделювання САУ. Дослідити поведінку САУ при варіації характеристик реакторів

5. Запропонувати рішення щодо модифікації програми моделювання для дослідження  системи при від-/підключеннях реакторів, при врахуванні динаміки реакторів.                    

Задачі другого рівня:

1.  Урахування в програмі того,  що реактори є інерційними об'єктами,

тобто вихід реактора визначається не алгебраїчним:

,

а диференціальним рівнянням:

.

2. Урахування в програмі того, що управління  (подача сировини не може бути від’ємною).

3. Модифікація програми для випадку 4-х реакторів, довільного числа реакторів.

4. Урахування в програмі повільного дрейфу характеристик реакторів (лінійні функції часу, інші функції).

5. Урахування в програмі підключення і відключення реактора в певні моменти часу.

6. Оптимальний регулятор не працює, коли немає перехідних процесів, тому в програму слід ввести тестові імпульси.

7. Модифікація програми – замінити простіші ПІ-регулятор та ПІД-регулятор на регулятори вектора стану.

Спочатку розглянемо альтернативні шляхи знаходження оптимального розподілення навантаження між реакторами.

Аналітичне розв'язання задачі

Очевидна альтернатива – управління процесом можна побудувати на безпосередньому обчисленні оптимальних значень виходу стиролу для кожного реактора. Потім ці значення встановлюються за допомогою відповідних локальних систем регулювання, що повинні їх підтримувати, змінюючи подачу етилбензолу.

Для знаходження оптимального розв’язку використаємо метод невизначених множників Лагранжа. Згідно з цим методом записуємо функцію Лагранжа:

 

(8.6)

Записуємо необхідні умови екстремуму цієї функції:

.

Додавши сюди рівняння обмеження отримаємо чотири рівняння для чотирьох невідомих  змінних – .

Підставимо конкретні значення функцій (4) і (5)  в  (6):   

.

Для знаходження аналітичних виразів похідних використаємо апарат символьних обчислень: 

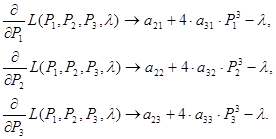
Вводимо значення параметрів функцій виробничих витрат для усіх реакторів: 

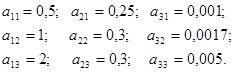
Вводимо значення обмеження та початкові значення шуканих змінних:

Записуємо і розв'язуємо числовим методом систему рівнянь, наприклад, в MathCad: 

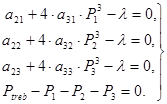
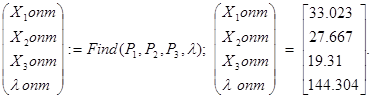
Контроль виконання обмежень:

.

Перевірка виконана, значення співпали.

Можна узагальнити цю задачу на випадок  реакторів, зробити розв’язання функцією значення обмеження . 

Розробка системи  управління реакторами

При розробці структурної схеми виходимо із визначених нами функцій системи управління технологічним процесом:

а) підтримка заданого рівня виходу стиролу;

б) оптимізація розподілу навантаження між реакторами.

Для виконання першої задачі поставимо ПІ (пропорційно-інтегральний)  регулятор. Виконання другої задачі ускладнено проблемами оперативного вимірювання характеристики . Замість цього використаємо індикатор – величину, що пов’язана з потрібною величиною монотонною залежністю. Такою величиною може бути похідна – вихід стиролу на одиницю подачі етилбензолу. 

Словесна модель регулятора оптимізації розподілу така (рис.8.5):

−     регулятор рівня подає однакові управління в усі реактори;

−     вимірюються "відгуки"  кожного з реакторів на це управління;

−     формуються відхилення від середнього, і з затримкою на такт;

−     на реактори подаються "вирівнюючі" управління. У результаті збільшується навантаження реакторів, у яких    вище середнього, а зменшується для тих реакторів, де  – нижче середнього.  Такий принцип перерозподілу дуже поширений. Для випадку монотонних випуклих функцій усталеним станом системи буде точка екстремуму.

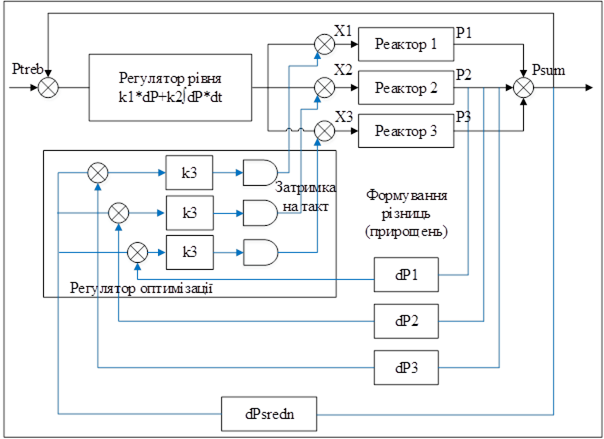
Рисунок 8.5 – Модель регулятора оптимізації розподілу

8.3 Оптимальне управління банківською системою

Ефективна система банків – одна з необхідних умов ефективності національної економіки і добробуту кожного громадянина. 

Потенційно банки оптимізують розподіл суспільних ресурсів між споживанням, накопиченням і розвитком. Клієнтами банків сьогодні є більша частина населення розвинених країн.

Банк – специфічна система масового обслуговування. Специфіка банківської діяльності у високому рівні конкуренції та "примхливості" клієнтів. Ці два фактори разом породжують високий рівень невизначеності і ризиків.

Загальновизнано, що рівень банку визначається інтенсивністю використання і якістю математичних моделей – засобів прогнозування і управління. Життя змушує банки розробляти необхідні робочі моделі. Однак корисні моделі не виходять за межі організації. У програмі залишається в першу чергу освіта – майбутніх спеціалістів навчають, в основному, на словесних та елементарних загальних моделях. Знання основ банківської діяльності потрібні сьогодні практично всім. Парадоксальний аспект проблеми моделювання банків в Україні в тому, що це "нічийна територія". Для спеціалістів з фінансів це "математика", для спеціалістів з технічних наук – це "економіка". Хто повинен розробляти моделі? Фінансист, програміст, математик? Це питання не розв’язується дискусіями. Далі подано процес побудови робочої моделі банківської системи на базі теорії  управління і системного аналізу.

Обсяг публікацій з банківської справи зростає експоненціально. У Росії і Україні щорічно видаються десятки посібників і підручників – своїх і перекладів з англійської. Однак публікацій з новими і конструктивними результатами небагато. Причини:

−     системні – концентрація і розсіювання знань по джерелах публікацій (закони Бредфорда, Зіпфа);

−     комерційні – ефективні моделі звичайно існують як "ноу-хау";

−     класифікаційні – помилкова класифікація задачі.

Переглянута література була поділена на три класи, які можуть перетинатись:

а) фундаментальні роботи з моделювання і управління;

б) навчальні посібники і підручники;

в) дисертації.

Особливістю літератури класів б) і в) є  вторинність – це поглиблення певної лінії, наприклад, моделі на базі міжгалузевого балансу, нечіткої логіки та нейронних мереж (особливо популярних в фінансових задачах) та ін. Виділено певні роботи – представники класів:

−     типові підручники для фінансистів;

−     підручники з елементами розробки моделей;

−     підручники фундаментального рівня;

−     класичні фундаментальні підручники–першоджерела.

В дисертаціях з банківської справи (захищених як за економічними, так і за технічними спеціальностями) виявлено багато цінних висновків і спостережень. Сьогодні з’являється все більше літератури безпосередньо з моделювання банківських систем. Однак все це не складається в єдину систему моделей.  Тому вирішено не узгоджувати знайдене в літературі, а розробити робочу модель (таку, що виконується в середовищі математичного пакета) з самого початку -  від твердо встановлених емпіричних законів банківської справи до робочих моделей функціонування банку. Це можна зробити з використанням методології конструювання математичних моделей. Робоча модель є інструментом для пошуку оптимальних, адаптивних і просто безпечних управлінь, і тут раціонально починати розробку з першоджерел з теорії управління.   

Сьогодні потрібні не стільки нові моделі для нових систем і процесів, скільки раціональні технології розробки математичних моделей, здатних відобразити об’єкт, що еволюціонує. Необхідний інший підхід до моделювання, зокрема, робота з моделювання, де формули, набрані в текстовому редакторі, є прикладом нераціональної технології конструювання моделей.

Постановка  задачі

Виділимо з численних тактичних і стратегічних задач банку базову задачу: "дешево брати в оренду гроші" і "дорого здавати". Виправданням для такої грубої моделі є те, що над нею потім можна необмежено виконувати операції надбудови (розбудови). На рисунку 1 наведено схему банківської системи, що відповідає базовій задачі банку.

Ця схема подібна схемі двоканальної системи автоматичного регулювання. Одразу можна побачити одну з головних причин складності – непрогнозований і метаморфозний об’єкт управління – клієнти. Однак велика кількість і різноманітність клієнтів є скоріше фактором спрощення – в умовах стабільної національної економіки можна усереднювати та агрегувати характеристики клієнтів

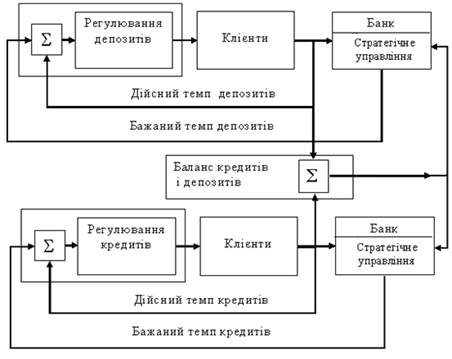
Рисунок 8.6 – Схема банківської системи

На жаль, в певних умовах поведінка клієнтів буває уніфікованою і детермінованою – це панічне вилучення коштів з банку. Банки, на відміну від виробничих і торгівельних організацій, певним чином зростаються з клієнтами. Очевидно, що треба розглядати банк і клієнтів як єдину банківську систему: банк повинен створювати процвітаючих і надійних клієнтів, а клієнти повинні дбати про ефективність і надійність свого банку. 

Розробка функціональних моделей

Отже, проведемо розробку моделей в середовищі математичного моделювання MathCad.

Потоки (темпи) депозитів і кредитів мають певну структуру – розподіли за тривалістю, відсотковими ставками, надійністю та ін. На першому етапі розглядаємо агреговані усереднені характеристики цих потоків. Працездатну агреговану модель потім неважко модифікувати для врахування структури потоків. Підсистема „депозити” перетворює вхідний темп депозитів у вихідний згідно з правилами і умовами вкладання коштів на депозит і зняття їх. Вхідний темп депозитів залежить від багатьох чинників: ставки депозиту, зростання економіки, темпу інфляції, конкуренції, настроїв і сподівань клієнтів та ін. На першому етапі розглядаємо тільки залежність темпу депозитів від середньої ставки депозиту.   

Модель вхідного темпу депозитів

Будемо вважати стан економіки і стан банку (частку фінансового ринку) стабільними. Припускаємо, що кожному рівню ставки депозитів відповідає певний усталений темп депозитів, тобто існує монотонно зростаюча функція ставки депозиту , де   – ставка депозиту,  – потенційний (максимально можливий для даного регіону і періоду часу) темп депозитів.

Реальний темп депозитів тільки в ідеальних умовах досягатиме усталеного рівня. Цей процес залежить від темпу зростання інформованості клієнтів, наявності прикладу і порад інших клієнтів, а також від ірраціональних та випадкових факторів. Сукупну дію названих факторів на потенційних клієнтів при зміні ставки депозиту задаємо різницевим рівнянням першого порядку.

,

де  –  поточний темп депозитів;

       – крок обчислень; 

        – коефіцієнт реакції темпу депозитів на зміну ставки.

Враховуємо також сезонність та випадкову складову і формуємо відповідний програмний модуль (рис.8.7).  

Рисунок 8.7. – Програмний модуль

Модель вихідного темпу депозитів

Модель вихідного темпу депозитів формуємо у виді програмного модуля, текст якого подано на рис. 8.8

Рисунок 8.8 – Модель вихідного темпу депозитів

Входи програмного модуля – ставка депозитів , середній термін депозиту і вхідний темп депозитів (фактично це програмний модуль вхідного потоку депозитів), виходи – вихідний темп депозитів без урахування залишків, залишки депозитів.

Модель вхідного темпу кредитів

Як і для темпів депозитів, припускаємо, що кожному рівню ставки кредитів відповідає усталений темп кредитів, тобто існує монотонно спадаюча функція ставки кредиту , де  – ставка кредиту,  – потенційний (максимально можливий для даного регіону і періоду часу) темп кредитів.

Реальний темп кредитів тільки в ідеальних умовах досягатиме потенційного рівня – зі  зростанням інформованості клієнтів, дії прикладу інших клієнтів, дії  ірраціональних та випадкових факторів. Процес реакції потенційних клієнтів на зміну ставки кредиту задаємо різницевим рівнянням першого порядку

,

де  – поточний темп кредитів; 

       – крок обчислень; 

        – коефіцієнт реакції темпу кредитів на зміну ставки.

Враховуємо також сезонність та випадкову складову.

Модель вихідного темпу кредитів

Модель вихідного темпу кредитів формуємо на базі вбудованої фінансової функції пакету "виплата боргу рівними частками протягом терміну кредиту":

.

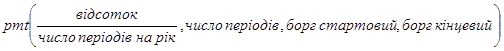Вихідний потік буде визначатись виразом, подібним інтегралу згортки:

,

де  – крок моделювання;

        – середня тривалість кредиту;

        – ставка кредиту;

       – значення вхідного темпу кредитів в дискретний момент часу .   

Природно використати математичну модель банківської системи для пошуку ефективних або безпечних управлінь. На першому етапі поставимо за мету – сформувати закони управління банківською системою на базі застосування методології і методів теорії управління. Цілі управління для першого етапу – максимізація доходу банку та балансування темпів кредитів і депозитів. Потім на базі працездатної моделі можна розглянути більш тонкі управління – згладжування вхідних темпів кредитів і депозитів, диференціювання ставок, урахування прогнозів валютних курсів, економічних показників та ін. Розглядаємо як змінні управління ставки кредитів і депозитів

Логіка управління

Виділимо "логічні управління": управління балансом і управління для оптимізації доходу. Управління для збалансування темпів кредитів і депозитів повинно одночасно змінювати ставки кредитів і депозитів так, щоб темпи "йшли назустріч". Для першого наближення беремо простіший, пропорційний закон управління балансом:

зміна ставки кредиту:

;

зміна ставки депозиту:

,

де  – "коефіцієнти підсилення";

          – різниця темпів депозитів і кредитів (помилка регулювання).

Різні знаки обумовлені тим, що для збільшення темпу кредитів треба зменшувати ставку, а для збільшення темпу депозитів – збільшувати її. 

Управління доходом банку відноситься до іншого класу – екстремального: потрібно не стабілізувати значення доходу на якомусь заданому рівні, а максимізувати за рахунок вибору значень ставки кредиту  –. Ставка депозиту прив’язується до ставки кредиту за рахунок умови збалансування темпів кредитів і депозитів.

Логіка екстремального управління така: на поточному кроці визначаємо приріст доходу за попередній період,якщо дохід зростає – продовжуємо змінювати  управління в тому ж напрямку, що і на попередньому кроці, якщо дохід зменшується – змінюємо управління в протилежному напрямку.

Це досить примітивна і наївна логіка "індикаторної поведінки". Можна її удосконалювати введенням фільтрації (не реагувати на випадкові та короткочасні збурення) і прогнозування (реагувати не тільки на зміну доходу, але і на тенденції зміни доходу). Перекладаємо ці міркування на мову рівнянь та алгоритмів. Розглянемо також банківську систему, як систему "попит-пропозиція":

−     відсоткова ставка – це ціна грошей;

−     залежність "ставка кредиту – темп кредитів" – це крива попиту на гроші;

−     залежність "ставка депозиту – темп депозитів" – це крива пропозиції грошей.

На рисунку 8.9 подано постановку і розв’язання задачі про оптимальну різницю ставок – якщо існують монотонно спадна функція попиту на кредити і монотонно зростаюча функція пропозиції депозитів, то існує оптимальна різниця ставок, що дає  максимум процентного доходу. Бачимо, що задача пошуку оптимальної різниці ставок еквівалентна геометричній задачі про вписаний прямокутник з максимальною площею. Можемо побачити також, що найбільший рівноважний стан досягається при рівних ставках кредиту і депозиту.  

Зміна ставок кредитів і депозитів визначається дією двох розглянутих регуляторів:

,

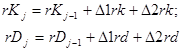де  ,  – управління від регулятора балансу;

          , – управління від екстремального регулятора.

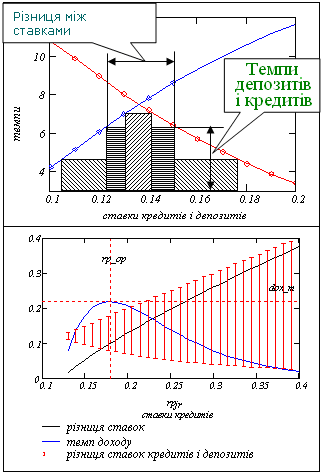
Рисунок 8.9 – Постановка і розв'язання задачі про оптимальну різницю ставок

На рисунку 8.10 подано схему програми моделювання. Інакше це називається "програма в псевдокодах".  Програма складається з функціональних модулів, розглянутих вище, – вхідних і вихідних темпів кредитів і депозитів, трендів і  невизначеностей, алгоритмів управління. За рахунок настроювання і заміни модулів програма дозволяє відобразити будь-яку специфіку функціонування банківської системи. Програма написана в середовищі мови програмування математичного пакета MathCad. Ця мова максимально наближена до природної мови математики, тому текст програми практично не відрізняється від запису системи рівнянь математичної моделі. Саме тому використовуємо термін "робоча модель".  

Рисунок 8.10 – Схема програми моделювання

Входи програми зібрані у матрицю з вісімнадцяти параметрів, вихід програми – десять дискретних функцій часу: вхідні і вихідні темпи депозитів, баланси "вхід-вихід" кредитів і депозитів, ставки кредитів і депозитів, загальний баланс банку  та баланс вхідних темпів кредитів і депозитів.

Технологія конструювання моделей ставить специфічні вимоги і до тексту програми  і до інтерфейсів. Це можливість доступу до всіх елементів програми, орієнтованість інтерфейсу на обчислювальний експеримент. Вхідні дані для програми (рис. 6) вводяться з коментарями, у "змістовному вигляді", а потім збираються у матрицю параметрів . У першому рядку матриці зібрані параметри вхідних і вихідних потоків кредитів, в другому – те ж саме для депозитів.        

Результати тестування програми

Програма моделювання не мала прототипів, тому виконано комплексне тестування для перевірки:

−     "синтаксичної" коректності (виявлення банальних помилок – втрачених складових і переплутаних знаків);

−     "семантичної" коректності (перевірка результатів моделювання при нульових та рівних ставках, при однакових термінах кредитів і депозитів);

−     "прагматичної" коректності (відповідність статистичним даним, можливість настроювання і модифікації програми).

Спочатку була випробувана модель з фіксованими ставками кредитів і депозитів, потім у модель був введений модуль управління з найпростішими законами управління – пропорційними. На рисунку 8.11 наведено приклади двох реалізацій перехідних процесів на відповідних фазових площинах з урахуванням випадкових збурень. 

Рисунок 8.11 – Приклади двох реалізацій перехідних процесів на відповідних фазових площинах з урахуванням випадкових збурень

Перехідні процеси на фазовій площині для випадків стартової ставки кредиту нижче і вище оптимальної наведені на рис. 8.12

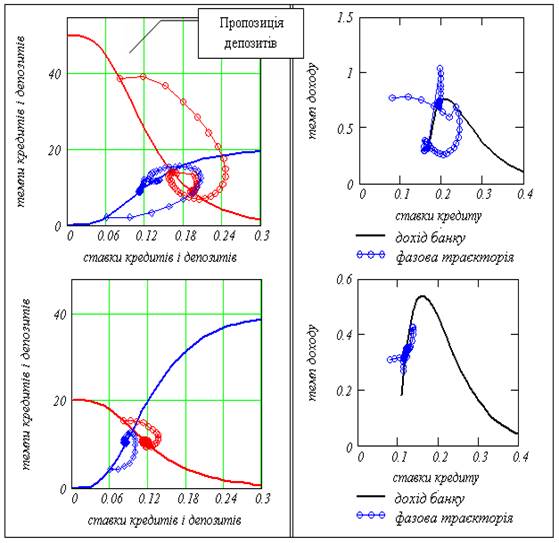
Рисунок 8.12 – Перехідні процеси на фазовій площині для випадків стартової ставки кредиту нижче і вище оптимальної

Бачимо, що:

а) підсистема стабілізації балансу вхідних потоків кредитів і депозитів працює задовільно;

б) підсистема максимізації доходу є незадовільною: не в усіх випадках приводить систему до максимуму, іноді – взагалі робить систему нестійкою.

Причини незадовільності підсистеми максимізації:

а) підсистеми управління діють спільно на об'єкти управління, що може призводити до небажаної інтерференції;

б) занадто великі збурення і неоптимальні значення коефіцієнтів зворотних зв'язків: ;

в) алгоритм пошуку максимуму має органічний недолік – коли дохід майже незмінний, то припиняється оптимізація. 

На рисунку 8.13 подано перехідні процеси в часі для тих же умов, що і на рисунку 8.12. Можемо бачити, що система управління приводить ставки кредиту і депозиту досить точно до оптимального стану (11%, 9%) з початкових станів "малі ставки" та "високі ставки". 

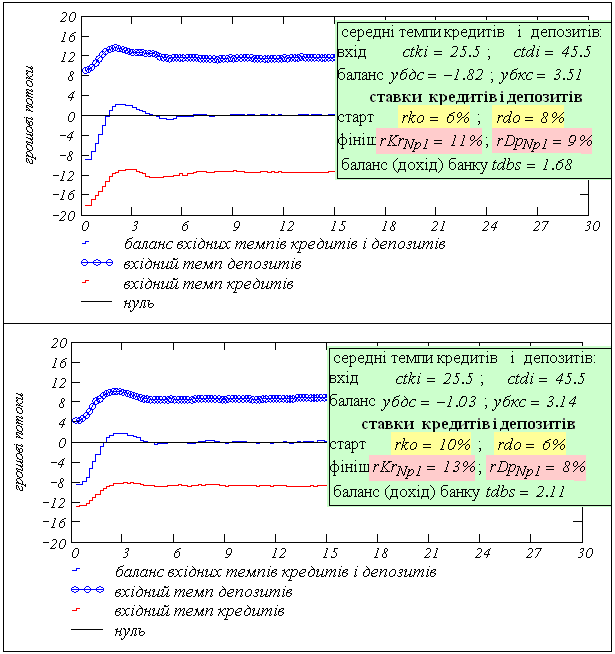
Рисунок 8.13 – Перехідні процеси в часі

Напрямки розвитку моделі банківської системи

Початкова ціль розробки була в створенні максимально спрощеної математичної моделі банку як системи масового обслуговування. Розробка повинна була дати і дає можливість студентам виконувати експерименти над віртуальною реальністю; дає початкове розуміння суті банківської справи: джерела нестійкості і виникнення "безпричинних" банкрутств. Робочу модель довелось будувати "з нуля". Навіть найпростіша з реалістичних моделей виявилася досить об’ємною. Однак ця модель базова – вона дозволила відносно легко враховувати і досліджувати різноманітні аспекти банківської діяльності. У даній лекції як приклад розширення подано моделі управління банком. Крім цього були розроблені моделі темпів кредитів і депозитів з урахуванням інфляції, конкуренції та панічної поведінки клієнтів. Чисто технічною задачею є модифікація моделі для врахування диференціації ставок кредитів і депозитів а також диференціації клієнтів. Розроблені на базі класичних портфельних задач субмоделі для оптимізації структури активів і пасивів.