Попередня сторінка          Зміст           Наступна сторінка          Електронні посібники ВНТУ

 

9 АДАПТИВНІ САУ

 

9.1 Адаптивні САУ з настроюванням власної частоти

9.2 "Швидка" адаптивна САУ

9.3 Адаптивна САУ на базі нечіткої логіки

9.4 Адаптивна САУ на базі нейронної мережі

 

9.1 Адаптивні САУ з настроюванням власної частоти

 

Проблеми при впровадженні адаптивних САУ у інженерну практику. Класифікація адаптивних САУ

 

Як відомо, адаптивні САУ є нелінійними і нестаціонарними, навіть якщо об’єкт управління – лінійний. При впровадженні адаптивних САУ у масову інженерну практику можна виділити три класи проблем:

−  проблеми реалізації складних, нелінійних алгоритмів, що "остаточно" вирішилися на базі сучасних апаратно-програмних платформ, але виявився брак життездатних схем і концепцій для адаптивних САУ;

−  проблеми міжгалузевих бар'єрів. Традиційно, в першу чергу, адаптивні САУ розробляли для об'єктів авіаційної та ракетно-космічної техніки, в інші галузі (у нас) цей досвід з відомих причин не переносився;

−  проблеми небезпечності адаптивних САУ. Стисло це можна сформулювати як емпіричний закон (з виключеннями): чим більше інтелекту ми вкладаємо в систему, тим більш дорожчими і різноманітнішими будуть її відмови.

Адаптивні САУ поділяються на два класи:

- аналітичні;

- пошукові.

В аналітичних налаштування параметрів регулятора відбувається за рахунок відомої аналітичної залежності між значеннями параметрів об'єкта, збуреннями і параметрами регулятора.

В пошукових адаптивних САУ налаштування відбувається за результатами пошуку деяким методом “спроб і помилок”.

Сьогодні використання систем автоматизованого проектування (САПР) стало необхідною умовою будь-яких технічних систем. Непоміченою, в силу очевидності, концептуальною основою сьогоднішніх САПР є те, що середньостатистичний коефіціент новизни, оточуючих нас технічних систем і виробів, становить 2-5%. Принципово нові вироби і технології є рідкісними, епохальними подіями.

Якщо виділити і параметризувати структуру якогось класу технічних систем, то проектування при малих значеннях коефіціенту новизни можна звести до заповнення розробником специфікації (фрейма) об’єкту даного класу. Якість результату буде обумовлена трьома факторами:

−  якістю фрейма;

−  повнотою бази знань (попередніх розробок);

−  кваліфікацією розробника.

Направляючий фрейм-сценарій (НФС) заповнення специфікації об’єкту є фактично спеціалізованою експертною надбудовою над іншими –оптимізаційно-розрахунковими і креслярсько-графічними модулями САПР. В цій “екологічній ніші” експертних систем існують зразки настільки ефективні, що сам факт їх існування  буває “фірмовим секретом” розробника, а фрейм описується в термінах “це схоже на гру у сім питань”. Між іншим така методологія (“мова виконуваних специфікацій”) є стандартом Міноборони США для розробки програмного забезпечення.

Вибір структур і алгоритмів адаптивної САУ теж може бути автоматизовано використанням відповідного НФС розробки. НФС є лінгвістичною моделлю об’єкта проектування, такою, що коректні відповіді спеціаліста на питання НФС породжують специфікацію системи, реалізація якої може бути повністю автоматизована. Для програмних систем це означає, що специфікація автоматично транслюється у робочу програму. Розробка ефективного НФС вимагає певного концептуального бачення проблеми.

Розглянемо приклад роботи з можливим НФС розробки адаптивної САУ – питання і вибрані відповіді. 

«Основний контур системи?» - Об'єкт управління (для прикладу) – 3-ого порядку з такою інтерпретацією компонентів вектора стану: x – координата; v – швидкість, w – прискорення.  Закон управління – лінійний, по вектору стану. Вектор управління – одномірний:    .

«Об'єкт настройки?» – Параметри  регулятора. 

«Метод настройки?» – З можливих альтернатив настройки параметрів регулятора вибираємо ітеративний метод, тобто контура самонастройки зі зворотним зв’язком, що підтримує задане значення показника якості регулювання.

«Показник якості перехідного процесу? (керована змінна контура самонастройки)» – З можливих альтернатив – від узагальненого  інтегрального квадратичного критерія до перерегулювання – вибираємо показник-індикатор, а саме частоту коливань у перехідному процесі, або власну демпфовану частоту d.

Індикатор – вимірювана або спостережувана змінна, пов’язана монотонною залежністю з основним критерієм якості, інші назви – підціль, псевдоціль, робочий критерій.

«Засоби дії на показники якості управління в основному контурі?» – Вибираємо безпосередню зміну параметрів регулятора  – це будуть управляючі змінні контура самонастройки. У сучасних цифрових регуляторах це потребує тільки зміни параметрів програми управління.

«Спосіб вимірювання власної частоти ?» – З можливих альтернатив: перетворення Фур’є, виділення періодичного сигналу з нормалізацією і підрахунком переходів через нуль, вибираємо вимірювання  різниці частот  за допомогою двох аналогових фільтрів або дискретних фільтрів з протилежними частотними характеристиками.

 – потрібне значення частоти, що обумовлене потрібною швидкодією основного контуру.

7. «Спосіб забезпечення вхідної інформації?» – Щоб вимірювати показники перехідного процесу (ПП) треба стимулювати перехідні процеси. Можливі альтернативи стимуляції ПП:

а) періодично подавати імпульси на вхід основного контура;

б) подавати шум;

в) нічого не подавати, якщо в основному контурі досить шумів та управляючих сигналів.

Для професіонала відповіді  на питання (1 – 6) є майже вичерпними для  побудови адаптивної САУ, блок-схему якої подано на рисунку 9.1.

В цьому прикладі вибрано варіант, коли потрібна якість управління Qz  задається  непрямо – еталонною власною демпфованою частотою .  Дійсна частота  при коректному виборі параметрів регулятора  є монотонною функцією  параметра регулятора  – "штрафа за помилку", а тривалість перехідного процесу  приблизно пропорційна .  Таким чином,  – параметр досить просто вимірюваний і досить просто пов'язаний з іншими параметрами САУ:  монотонно змінює значення , яке монотонно пов’язане з .

 

 

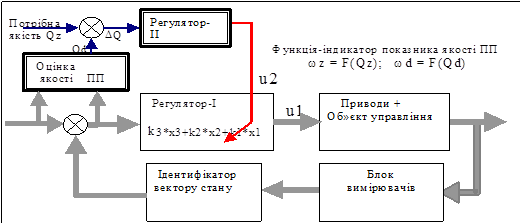
Рисунок 9.1 – Блок-схема адаптивної САУ

 

Розробка блок-схеми і математичної моделі частотного дискримінатора

 

 

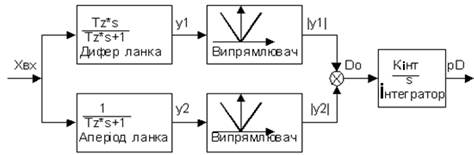
Згідно з «лінійною логікою» слід вибрати метод та пристрій для оптималь,ного вимірювання «чистої» частоти . Розглянемо дві альтернативи реалізації вимірювача частоти – аналогову на базі двох лінійних фільтрів і випрямлячів (рис. 9.2) і програмну реалізацію на базі еквівалентної дискретної моделі цієї аналогової системи.

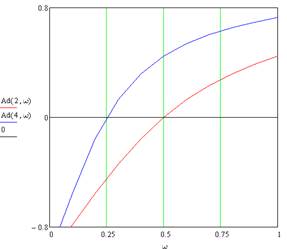
Рисунок 9.2 – АЧХ для двох значень власної частоти

 

Записуємо вираз для різниці , будуємо графіки. Бачимо, що характеристики такого вимірювача частоти нелінійні:

 

            

Ще один недолік схеми – вихід пропорційний не тільки частоті, але і амплітуді вхідного сигналу. Але, як  побачимо далі, цей недолік є дуже великою перевагою. Єдиним реальним недоліком схеми є неможливість використання лінійних методів, що вимагає використовувати технології розробки, орієнтовані на імітаційне моделювання.

Сьогодні в багатьох випадках обробку сигналів вигідніше виконувати в цифрових пристроях. Побудуємо еквівалентну дискретну математичну модель частотного дискримінатора, в якій окремі рівняння відповідають елементам аналогової схеми.

 

     

 

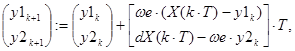
У цій моделі імена змінних аналогічні означенням на рис. 9.3. Зокрема,  – виходи фільтрів;  – вхідний сигнал і його похідна;  – еквівалент інтегралу,  – його початкове значення.

 

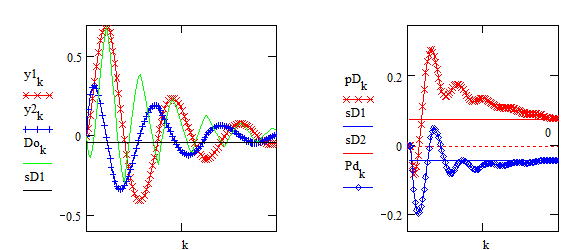
Рисунок 9.3 – Перехідні процеси в частотному дискримінаторі

 

Записані рівняння є виконуваними в середовищі математичного пакету, і водночас, це майже готова програма реалізації у мікропроцесорній системі. Як приклад досліджень цифрової реалізації  на рисунку 9.3 подано графіки процесів у дискримінаторі для випадку згасаючого гармонічного сигналу – імітації імпульсної перехідної характеристики (ІПХ). І для таких сигналів усталений вихід монотонно залежить від різниці частот. 

Аналітичне дослідження статичних і динамічних характеристик  частотного дискримінатора пов’язане із значними математичними ускладненнями, але можливе,  наприклад, на базі методу гармонічної лінеаризації.  Можна показати працездатність пристрою на більш складних за спектром вхідних сигналах. Але це зроблено вже за допомогою моделі повної адаптивної системи.

На цих графіках  i  – вихід дискримінатора і усталене значення для різниці частот  і  – теж саме для  .

 
Розробка математичної моделі САУ з системою самонастройки

 

Опорний параметр для системи самонастройки – власна демпфована частота, яка визначається в процесі синтезу основного контура, що є тривіальним для управління по вектору стану лінійним об’єктом і тому не наводиться. Подана далі система рівнянь разом з розташованими рядом графіками і зонами вводу є "стендом" для проведення обчислювальних експериментів.

Головні компоненти  "стенду" зібрані в межах однієї екранної сторінки, що дозволяє змінювати параметри, рівняння і оперативно спостерігати перехідні процеси.  Можливі такі альтернативи відображення моделі  САУ на стенді – реалістичне відображення, блок-схема системи, математична модель (система рівнянь) і гібридні варіанти.

Для розробника-професіонала алгоритмів управління і професіонала у предметній області об’єкта управління найзручніша альтернатива – повністю прозора і відкрита для змін, онлайново діюча (live) математична модель. Проблеми виникають тільки з розташуванням в межах одного екрану моделі високого порядку. Але, як відомо, складніша модель не обов’язково точніша.

На рисунку 8.16 подано спрощений приклад такого стенду з настроюванням тільки одного параметра  регулятора –  і без елементів управління експериментом. Для настроювання періодично подаються імпульси (функція ,  де  – кількість тактів квантування між імпульсами). 

Фактично це система нелінійних різницевих рівнянь 7-го порядку. Перші три рівняння описують динаміку об’єкта управління. Рівняння (4 – 6) описують частотний дискримінатор, а останнє рівняння – вихід контуру самонастроювання. Користувач може вводити параметри як у зонах вводу – кнопками, спіннерами, слайдерами, так і безпосередньо у самих рівняннях.

Якість контура самонастройки визначають два параметри: K1 – "штраф за помилку" власної частоти;  – параметр згладження вихідного сигналу дискримінатора. Ці параметри можуть бути вибрані аналітично (для лінеаризованої моделі контура самонастройки) і пошуковими методами:

а) "вручну" в середовищі цього документу, за 10-25 хвилин;

б) за допомогою пошукової  системи, що фактично буде контуром самостройки 3-го рівня.

 

 

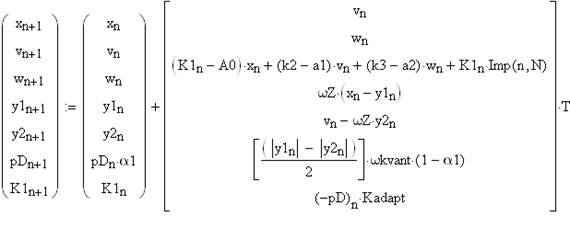
На рисунку 9.5 наведено приклади перехідних процесів у адаптивній САУ для випадків початково нестійкого основного контуру. Вибрано аперіодично нестійкий без управління об’єкт класу “нестійкий маятник”, тому основний контур має дві границі стійкості по параметру  – верхню (велике  і коливальна нестійкість), і нижню (мале  і аперіодична нестійкість).

 

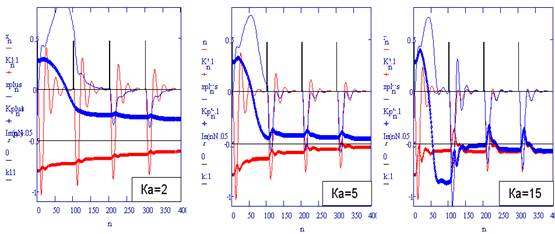
Рисунок 9.5 – Перехідні процеси у адаптивній САУ при різних значеннях 

На цих графіках тонкі лінії – перехідні процеси в основному контурі – реакції  на тестові імпульси, що подаються з певним періодом, жирні лінії перехідні процеси в контурі адаптації (самонастроювання), тобто зміна параметру  основного контуру (штрафу за помилку координати). Горизонтальні лінії – потрібні виходи основного контуру (нульова помилка координати) і контуру адаптації – розрахункове значення , яке забезпечує вибраний (заданий) перехідний процес в основному контурі.

Зауваження. Для прикладу на етапі синтезу основного контуру вибрано перехідний процес з підвищеною коливальністю.

Неважко на даній системі моделювання поставити інші обчислювальні експерименти. Розглянемо приклад дослідження впливу шумів в основному контурі. Ці шуми, з одного боку – завади, збурення, з іншого – стимулятор реакцій основного контуру, тобто джерело потрібної для самонастроювання інформації. Для моделювання системи за наявності шумів достатньо сконструювати функцію Шум(.) і замінити нею функцію генерації тестових імпульсних сигналів Imp(.) у «стенді».

 

 

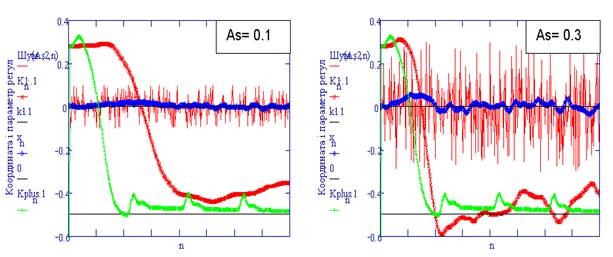
Рисунок 9.6 – Вплив шумів в основному контурі

 

На рисунку 9.6 подано графіки перехідних процесів в адаптивній САУ при дії шумів різної амплітуди (As=0.1, As=0.3). Дослідження дозволяють зробити висновок, що в певному діапазоні амплітуди As шуму, САУ буде стійкою і задовільною, але процес адаптації стає ймовірнісним і в середньому повільнішим, ніж при дії імпульсних тест-сигналів. На графіку для порівняння подано процес зміни  при дії імпульсних тестових сигналів. За занадто малої амплітуди шуму настроювання стає повільним, а при великій – контур адаптації працює нестабільно.

 

9.2 "Швидка" адаптивна САУ

 

Визначимо термін – "швидка". Класичні адаптивні САУ з підручників і монографій виникли як надбудови над звичайними регуляторами. Контур адаптації в такій САУ формував інформацію про якість перехідного процесу і згідно з цим змінював параметри регулятора основного контуру.

Номінально в такій САУ мало місце запізнювання на величину тривалості перехідного процесу. З урахуванням шумів, накопичення даних і фільтрації запізнення могло бути ще більшим. Такі адаптивні САУ могли успішно працювати на об’єктах з дуже повільною зміною параметрів.

Для випадків, коли параметри об’єкта значно змінюються (більше 10% за період перехідного процесу), потрібні інші рішення. Одне з таких рішень подається в даній лекції. Суть його в тому, що під певний клас об’єктів і певний клас структур регуляторів (лінійний, релейний) можна знайти, підібрати параметризовані ПРАВИЛА зміни параметрів регулятора, виходячи з прогнозу поведінки об’єкта на базі значень поточного вектора стану.

Правило – певне висловлювання, наприклад: "якщо компоненти вектора стану задовольняють певне відношення , то змінити параметри регулятора згідно з алгоритмом ".

Такі правила фактично задають розбиття простору стану на класи еквівалентності. Знаходження правил – нетривіальна задача, тому існує метаправило: якщо правило працездатне, не слід робити його загальновідомим.

 

Розробка базової програми моделювання "швидкої" адаптивної САУ

Прочитаємо дані з файлів:

 

Розшифровуємо  дані з файлу:

     – номінальні параметри регулятора;

     – номінальні параметри об’єкта;

     – вимоги до якості регулювання.

 

Виводимо для контролю дані – номінальні параметри регулятора  та параметри моделі об’єкта:

 

задаємо кількість кроків моделювання:

 

 

Записуємо компоненти  математичної моделі об’єкта та початкові умови

 

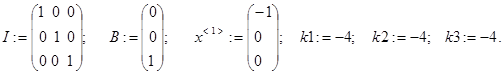
Задача 1. На базі поданої вище інформації, використовуючи формули, побудуйте схему адаптивної системи.

Задаємо крок  точність обчислень  Вводимо розширений вектор стану, задаємо початкове значення вектора параметрів регулятора:

 

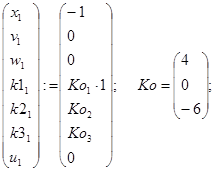
        – параметр настроювання.

 

 

Вводимо значення параметра настроювання і записуємо рівняння системи: перші три рівняння - 1, 2, 3 - описують динаміку об’єкта управління певного класу; рівняння 4, 5, 6 – настроювання параметрів об’єкта за певними правилами; рівняння 7 – регулятор.

 

 

 

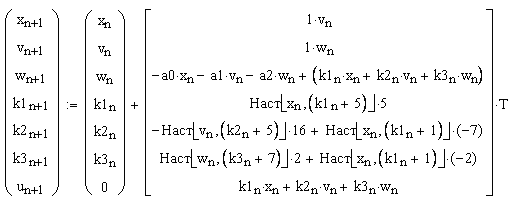
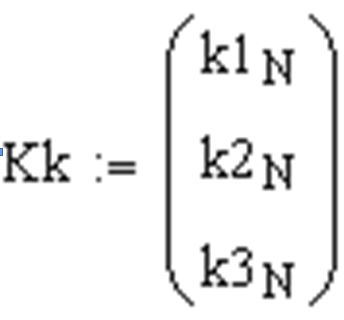
Задача 2.Дивлячись на систему рівнянь вище, зробіть програму моделювання адаптивної САУ. Визначте через цю програму функцію користувача за таким зразком.

 

Будуємо графіки перехідних процесів в системі.

 

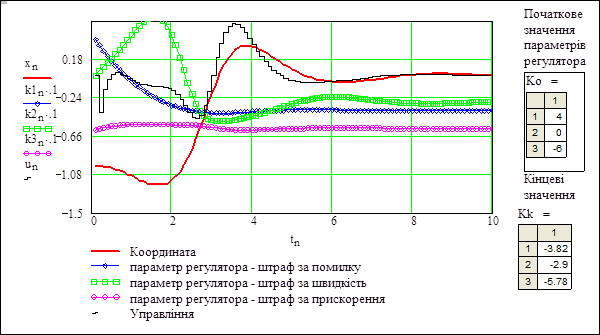
Рисунок 9.7 – Графіки перехідних процесів в системі

 

Перший об’єкт дослідження – залежність кінцевих значень параметра  регулятора від початкових – нагадуємо, що ми досліджуємо суттєво нелінійну і нестаціонарну систему. Вводимо  початкове, а виводимо кінцеве значення. Також вводимо змінні для графіків. 

 

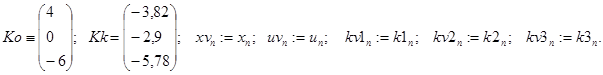
Подивимось на графіки (рис. 9.7): наведено перехідні процеси для нестійкого недемпфованого об’єкта з нестійким на початку регулятором. Бачимо, що процеси стабілізації об’єкта і процеси настроювання закінчуються одночасно. Система в цілому стійка.

Дивимось ще вище на систему рівнянь. Бачимо, що настроювання всіх параметрів регулятора  виконується функцією Наст (Координата, Параметр регулятора), в яку власне "вкладена" вся складність алгоритму настроювання.

Бачимо очевидну недосконалість системи: велику кількість чисел – параметрів "підстроювання" системи самонастроювання. Якщо неможливо раціонально задати ці параметри (аналітично чи через певні процедури), то це означатиме нежиттєздатність даної адаптивної системи. Залишаємо цю проблему для самостійного розв’язання.

Бачимо очевидну обмеженість моделі об’єкта управління: це "динаміка матеріальної точки з ненульовою масою". Це вузький для теорії і поширений для практики клас динамічних систем. Згадаємо задачі термінального управління попереднього семестру – там ми теж почали з розгляду руху матеріальної точки.

 

Дослідження  "швидкої" адаптивної  системи. Вплив початкових умов

 

Ми отримали не стільки ключ до знань, скільки інструмент – "відмичку". Проведемо серію пошукових експериментів на моделі адаптивної системи. Далі подано серію копій екрану. На графіку (рис. 9.8) наведено перехідні процеси для координати, параметрів закону управління, управління та числові значення параметрів управління в початковий і кінцевий моменти процесу. 

 

 

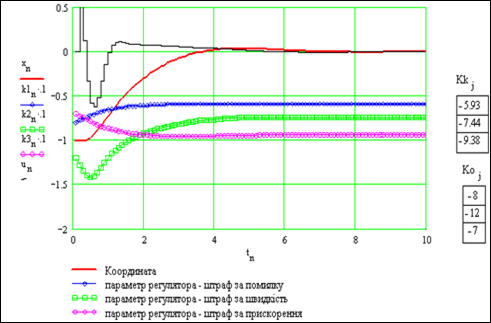
Рисунок 9.8 – Перехідні процеси для координати, параметрів закону управління, управління та числові значення параметрів управління в початковий і кінцевий моменти процесу

 

Бачимо, що параметри регулятора змінюються несуттєво – система є задовільною.

 

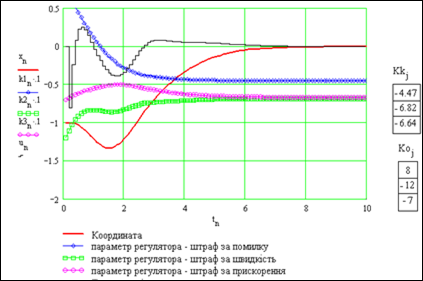
Рисунок 9.9 – Зміна параметрів регулятора

 

Бачимо на рисунку 3, що час перехідного процесу по координаті збільшується порівняно з попереднім випадком – з 4 до 6. В цілому всі процеси стійкі. Кінцеві параметри регулятора приблизно такі, як і в попередньому випадку. 

 

 

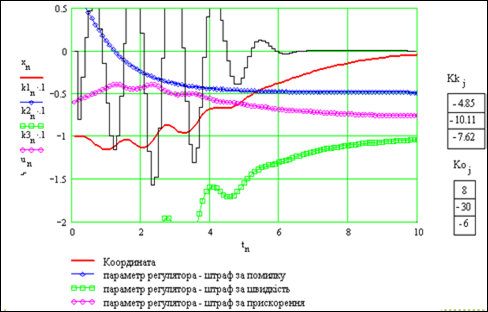
Рисунок 9.10 – Кінцеві параметри регулятора

 

Бачимо на рисунку 9.10, що перехідний процес по координаті не тільки розтягнутий, але й коливальний. Маємо коливання управління з великою амплітудою. Цей експеримент є цінним: ми знайшли "хворобу" нашої адаптивної системи.

Порівняно зі звичайними САУ наша система має антиінтуїтивну поведінку: при збільшенні початкового демпфування виникають високочастотні коливання управління. В цілому процес є стійким.

 

Дослідження "швидкої" адаптивної системи. Вплив параметрів настроювання

 

Запропонована адаптивна система – необґрунтована, невпорядкована, єдина позитивна якість – вона працює. В алгоритмі настроювання маємо десять параметрів. Природно припустити, що між ними є певні залежності, що їх число можна зменшити, що їх величини можна не підбирати, а розраховувати. Перший крок на цьому шляху – провести прості дослідження впливу цих параметрів на якість перехідних процесів в адаптивній системі.

Зробимо ще один екземпляр програмного об’єкта "рівняння  динаміки адаптивної системи". Змінюємо відповідні параметри і будуємо разом два набори перехідних процесів.

 

Тест. Якщо Ви достатньо орієнтуєтесь в динамічних системах, у формах опису їх динаміки (диференціальні, різницеві рівняння), то вам  неважко  визначити, який параметр "приховано" під псевдонімом Му_Му. 

   

 

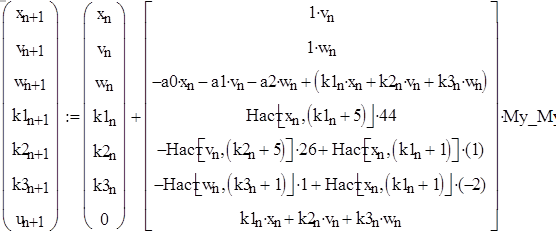
На рисунку 9.11 подано разом два перехідних  процеси – один для випадку, коли параметри регулятора більше номінальних, другий для випадку, коли параметри регулятора менше номінальних.

Термін "номінальне значення параметрів регулятора" має дві інтерпретації:

−     оптимальні значення параметрів, знайдені певним методом синтезу;

−     усталені значення параметрів, що є результатом функціонування адаптивної системи.

Для кожного процесу виведено по шість змінних – три координати вектора стану об'єкта і три параметри регулятора.

Бачимо, що система настроюється при довільних початкових значеннях параметра регулятора К1, якщо встановлені достатні значення К2 і К3. Система може настроїтись з нульового демпфування, якщо К1 є номінальним.

Можемо виділити такі  недоліки адаптивної  системи:

−     усталені помилки в контурі адаптації – при різних параметрах системи настроювання, коефіцієнти основного контуру К1, К2, К3 встановлюються на близьких, але різних значеннях;

−     не використано нечітку логіку.

Головна перевага адаптивної системи – процес настроювання виконується протягом перехідного процесу в основному контурі.

 

 

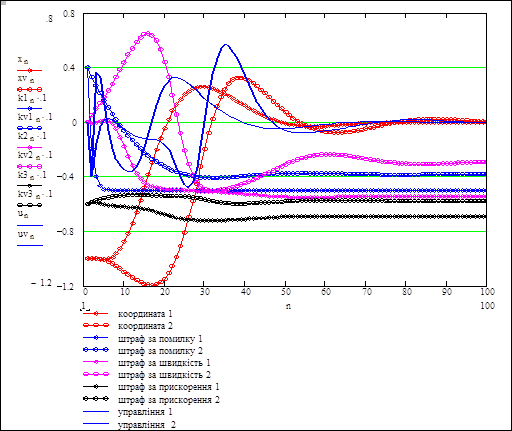
Рисунок 9.11 – Два перехідних процеси

 

Альтернативні методи отримання інформації для настроювання

 

– За рахунок чого настроювалася наша система?

– За рахунок аналізу поведінки системи в перехідному процесі.

– А якщо помилка в системі нульова, перехідні процеси відсутні?

– Ми вже знаємо, що в такому випадку настроювання не буде – вчаться саме на помилках.

Для процесу навчання (адаптації) слід забезпечити систему перехідними процесами помірного рівня: достатньо інтенсивними для навчання, і недостатньо – для виникнення нестійкості. Забезпечити адаптивну систему потрібною інформацією можна такими способами:

– періодична подача тестових імпульсів;

– подача гармонійного сигналу;

– подача "білого шуму".

Ці сигнали додаються до основного сигналу управління і є малими відносно середньої величини сигналу управління. Коли САУ працює в умовах постійних збурень і шумів (у вимірювачах та виконавчих елементах), то ці спеціальні сигнали для настроювання не потрібні.

Задаємо число кроків моделювання , дискретний час , початковий вектор стану 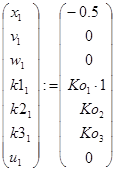 та параметри регулятора . 

 

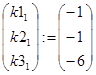Формуємо тестові сигнали:

гармонійні:   

;

 

випадкові:    

;

 

імпульсні:     

.

 

Задаємо параметри тестових сигналів: 

.

 

 

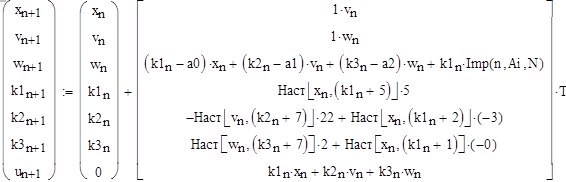
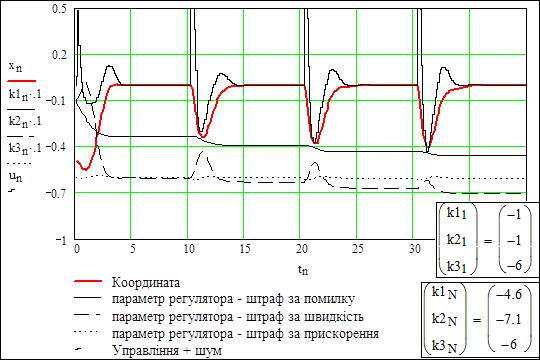
Рисунок 9.12 – Зміна нестійкої САУ на стійку

 

На рисунку 9.12 бачимо як спочатку нестійка САУ вже після першого імпульсу стає стійкою. Недолік даних імпульсних сигналів – ненульове середнє значення, слід чергувати додатні і від’ємні імпульси.

Система досить швидко настроюється під дією шумів (рис.9.13). Чим більше рівень шуму, тим швидше проходить настроювання, однак шуми – це збурення. Звичайно роблять рівень тестових шумів змінним – так, щоб вони зменшувались з часом. Однак це створює нові проблеми – надійності: все, що ми робимо змінним, може змінюватись зовсім в іншу сторону.

Використовуючи гармонійний тестовий сигнал, бачимо (рис.9.13), що процес настроювання подібний до процесу настроювання при випадкових сигналах. Побічна проблема – коефіцієнти регулятора мають гармонійну складову. Як і при інших видах тестових сигналів, слід вибрати їх оптимальний рівень.

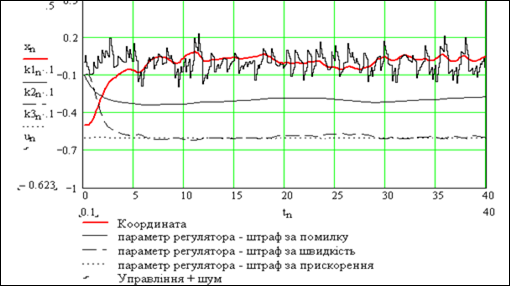
Рисунок 9.13 – Настроювання системи під дією шумів

 

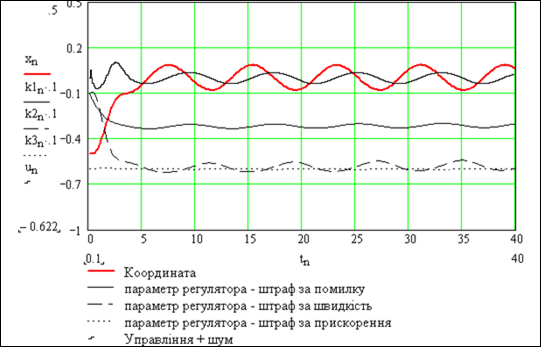
Рисунок 9.14 – Використання гармонічного тестового сигналу

  

Таким чином, отримали певну робочу гіпотезу, придатну, як мінімум для розбудови магістерської, кандидатської, інших видів дисертацій. Можна довести цю адаптивну систему до практичного використання.

У цій лекції отримали підтвердження головного принципу роботи з адаптивними та іншими інтелектуальними системами: завжди слід пам’ятати, що ці системи звичайно створюють більше проблем, ніж розв’язують. 

Розглянута система має ряд недоліків. Існують два шляхи усунення недоліків – настроювати "сторожів, щоб стерегти сторожів"  та збирати мережеві системи з альтернативних регуляторів, прямувати до певної диверсифікації.

При бажанні можна назвати ці системи: "штучні нейронні мережі", "штучні соціальні мережі", "колективи автоматів", "ансамблі динамічних систем", навіть "нейродинамічні системи". На жаль, ці властивості систем не позбавляють від необхідності думати. Однак думати слід за раціональними технологіями і предметно. Ця лекція – приклад предметного думання: гіпотези, висновки, рішення реалізуємо в середовищі математичного пакета MathCad, експериментуємо, і так отримуємо предметний матеріал для роздумів.

Це не "нова інформаційна технологія", а скоріше напівзабута інтелектуальна технологія. Відомо, що більшість видатних конструкторів зброї (лауреатів, академіків), починали слюсарями, і потім кожний елемент гвинтівки чи автомата випробовували тисячі разів своїми руками.

 

9.3 Адаптивна САУ на базі нечіткої логіки

 

Що таке регулятор? З фундаментально-філософської точки зору це просто відношення, перетворення, обернене до перетворення об'єкта управління:

 

;  ;  ;  ,

 

звідки маємо: 

 

.

 

Принцип оберненої моделі можна реалізувати методами нечіткої логіки – побудувати регулятор, що буде поступово настроюватись на динаміку певного невизначеного, нелінійного, нестаціонарного об'єкта управління. 

Справжня нечітка логіка досить незвична для осмислення. Тому почнемо з найелементарнішого прикладу – регулятора для статичного об'єкта. Між іншим цей приклад має певне практичне значення для побудови регулятора усталених станів для динамічного об'єкта.

Пройдемо крок за кроком увесь шлях від концепції до розробки програми реалізації адаптивного регулятора на базі нечіткої логіки.

 

Постановка задачі

 

Викладемо ідею нечіткого адаптивного регулятора, як вона подана в книзі М. Пешеля. Задано об'єкт управління, що описується в ідеальному випадку чіткою залежністю: 

 

.

 

Однак ця залежність з різних причин нечітка (неповністю визначена, розмита). Поставимо за мету (а не ціль, тому що поки не знаємо, як це зробити) розробку системи, що використовує інформацію про дійсну реакцію об’єкта для настроювання регулятора.

 

Конструювання розподілу нечіткості (функції належності) регулятора

 

Для того, щоб отримати змістовну (чітку) уяву про нечітку логіку, зробимо робочу модель нечіткої функції однієї змінної і поекспериментуємо з нею.

Задаємо параметри

 

. 

 

і чітку функцію:

 

.

 

"Розмиваємо" (фазифікуємо) цю функцію – задаємо певний двовимірний розподіл нечіткості.

 

,

 

де  .

 

Робимо це так:

−     задаємо параметр розмитості (дисперсія) 

 

;

 

−     у цілях економії інтелекту для розподілу нечіткості, використовуємо вбудовану функцію нормального розподілу:

 

.

 

Формат цієї функції:

 

dnorm (вхідна_змінна, математичне­­_очікування, дисперсія).

 

Задаємо розмір сітки:                                                                    

 

  та індекси:   .

 

Робимо програму для розрахунку масиву значень і будуємо тривимірні графіки функції розподілу нечіткості. Дивимось на графіки на рисунку 9.15. Бачимо нечітку залежність. На одному з графіків подано перетини, що відповідають розподілам нечіткості для відповідних значень вхідної змінної, на другому графіку – лінії рівня. Ми зробили величину нечіткості (дисперсію) пропорційною величині вхідної змінної. Це іноді відповідає реальності.

  

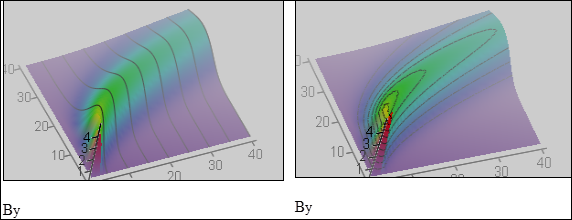
Рисунок 9.15 – Нечітка залежність

Вчимось маніпулювати віртуальною реальністю – витягнемо розподіли нечіткості:

 

 .

 

Ось що робить ця формула:

 

,

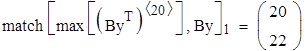тобто вона визначає координати максимуму розподілу нечіткості (характеристики регулятора при заданому значенні вхідної змінної j).

Задаємо пару значень:

.

 

Будуємо графіки (рис. 9.16).

 

 

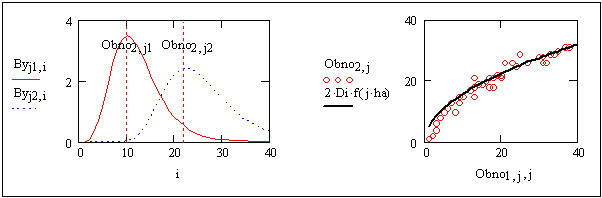
Рисунок 9.16 – Побудова графіків

 

На рисунку 9.16 наведені розподіли нечіткості для двох значень j1=5, j2=20, а також "чітка" функція регулятора на фоні максимумів відповідної функції розподілу нечіткості.

 

Конструювання алгоритму адаптації

 

Для реалізації і моделювання нечіткого регулятора потрібно вибрати і реалізувати такі функціональні модулі: 

1. Функція належності одного експерименту (проби): задано певний випадковий вхідний сигнал, який подано на модель об’єкта і отримано певний вихідний сигнал, що є результатом дії деякого чіткого механізму і різних видів невизначеностей (збурення, помилки вимірювання, квантові та інші властивості об’єкта). Можливо, що і вхідний сигнал реалізується з певними похибками. Треба задати відповідний двовимірний розподіл ймовірностей.

2. Імітація події: за допомогою певного генератора, відповідно до розподілу нечіткості, формується реалізація . 

3. Комбінування функції належності регулятора та проби. Альтернативи комбінування розглянуто далі.

4. Конструювання функції належності для об'єкта управління. Задаємо функцію розподілу нечіткості регулятора:

 

 ,

 

дискретизуємо цю функцію 

 

;  ;  ; ;  .

 

5. Конструювання функції належності для вимірювання виходу об'єкта управління. Задаємо функцію розподілу нечіткості проби (подали вхід – отримали вихід)

 

;  ;  .

Задаємо функції розподілу для декількох проб:

 

;

;

;

;

.

 

Записуємо альтернативи згортки розподілів нечіткості:

добуток:

;

сума:

.

 

На рисунку 9.17 подано настроювання нечіткого регулятора.

 

 

 

Рисунок 9.17 – Настроювання нечіткого регулятора

 

Конструювання програми функціонування системи з нечітким регулятором

 

З розглянутих вище компонентів збираємо програму (рис. 9.18). Достатньо нераціональну і недосконалу та помірно працездатну. Це, певним чином, перша проба. Число точок дискретизації функції розподілу нечіткості: 

 

.

 

Рисунок 9.18 – Збірка програми

Головний параметр для настроювання нечіткої характеристики регулятора 

 

 

 

 

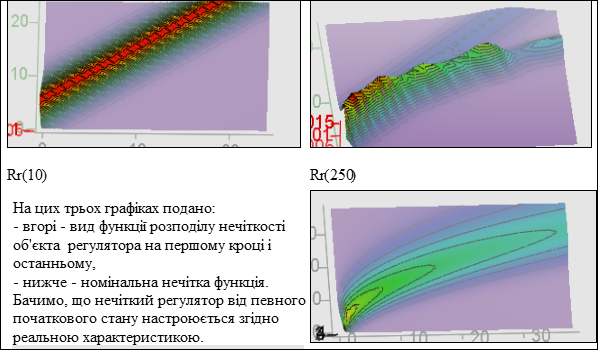
Рисунок 9.19 – Головний параметр для настроювання нечіткої характеристики регулятора

 

Таким чином, можливо зробити нечіткий ПІД-регулятор для об’єкта другого порядку і визначити, чи не ускладнюється побудова і настроювання такого регулятора. Розглянули середовище для випробування численних версій нечіткого регулятора. 

 

9.4 Адаптивна САУ на базі нейронної мережі

 

Нейронна мережа Кохонена

 

Інша назва мережі Kohonen's Self Organizing  Feature Map (SOFM) ("карта ознак Кохонена, що організується сама").

Ця мережа була запропонована Кохоненом в 1984 році. У цьому напрямку виконано багато робіт з модифікації базової моделі і побудови математичної теорії. Таке широке розповсюдження і велика кількість робіт можуть бути ознакою слабкої практичної корисності, тому що продуктивні напрямки зникають - стають фірмовими секретами.

У напрямку штучних нейронних мереж існує традиція виведення їх з дійсних чи гіпотетичних механізмів роботи мозку, хоч природно вивести її з моделей кінцевих автоматів і багатовимірних нелінійних імпульсних систем зі зворотними зв’язками - тобто моделей Я. Ципкіна.

Алгоритм Кохонена вважається подібним процесам, що відбуваються у мозку  при самонавчанні. Мережа Кохонена призначається для розділення векторів з певної множини на підгрупи - кластери. Мережа складається з М нейронів. При навчанні і роботі мережі на всі N входів кожного нейрона подається один і той же сигнал - N-вимірний вектор Х.  У процесі навчання змінюються "синаптичні ваги" нейронів. У книгах, наприклад, В. Круглова і В. Борисова вкрай неякісно перекладено матеріали - тексти і рисунки з першоджерел - це, певним чином, вторинні недоліки цього напрямку.

Вхідні сигнали - вектори дійсних чисел - послідовно подаються на входи мережі і виконується самонавчання. Після певного числа прикладів навчання закінчується і синаптичні ваги вже визначають кластери. Крім того, ваги організовуються так, що топологічно близькі нейрони схоже реагують на східні сигнали (вектори).

Для реалізації алгоритму необхідно визначити міру близькості нейронів. Розміри  зони близькості повинні зменшуватись.

Задаємо число нейронів  та число ознак , період  моделювання        

 

Алгоритм Кохонена

 

Крок 1. Ініціалізація мережі.

Коефіцієнтам мережі числом  присвоюються малі випадкові числа.  - початкова зона сусідства. Задаємо індекси ознак  та індекси нейронів  . Задаємо початкові значення ваги:

 

;

.

 

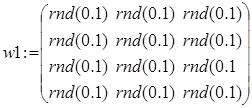Крок 2. Подача до мережі нового вхідного сигналу.

Крок 3. Обчислення відстані від  вхідного сигналу до кожного з нейронів за формулою:

 

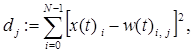
де  -  -ий елемент вхідного сигналу в момент часу  t;

      - вага зв’язку -го компонента вхідного вектора з -им нейроном.

 

Зауваження:

−     - "функція часу, що є -им компонентом вектор-функції часу ";

−      - формально це "-ий рядок матриці ";

−      - змістовно це "-ий компонент дискретизованої вектор-функції часу".

Щоб ефективно працювати в середовищі математичних пакетів потрібно сприймати кожен математичний об'єкт як єдиний в двох сутностях - неперервній і дискретній.     

Крок 4.  Вибір   -нейрона, для якого відстань    є мінімальною.

Крок 5. Настроювання ваг  для нейрона   та всіх сусідніх нейронів з зони сусідства   згідно з рівнянням:

  

,

де  - крок навчання , що зменшується з часом до нуля.

 

Введемо функцію:

 

.

 

Зробимо генератор тестових векторів. Закладемо в нього 4 класи об’єктів. Це тільки макет для створення узагальненої програми (рис. 9.20).

     

 

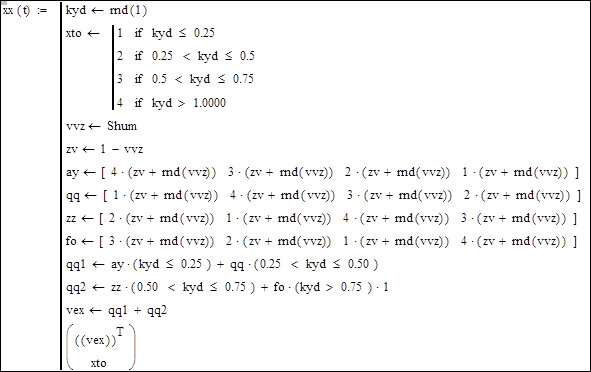
Рисунок 9.20 – Макет для створення узагальненої програми

 

Розпаковуємо вихід програми - генератора тестових послідовностей об’єктів класифікації

 

.

 

На рисунку 9.21 подано випробування модуля генерування тестових векторів.

 

 

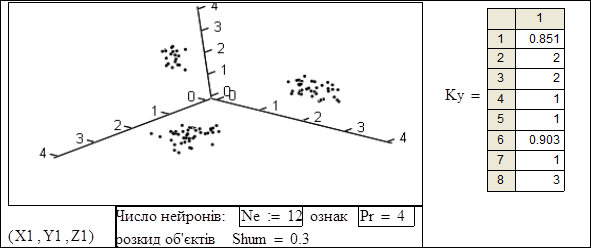
Рисунок 9.21 – Випробування модуля генерування тестових векторів

 

Крок 6. Повернення до кроку 2. На рисунку 9.22 наведено модуль "нейронна мережа Кохонена".

 

 

Рисунок 9.22 – Модуль "нейронна мережа Кохонена"

 

.

 

 

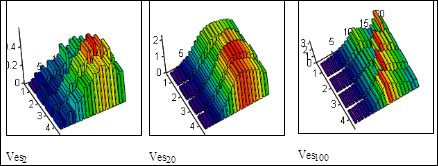
Рисунок 9.23 – Вивід модуля "нейронна мережа Кохонена"

 

Параметри процесу навчання:

−     розкид елементів кластерів  ;

−     стартова границя сусідніх нейронів  ;

−     звуження границь нейрона  ;

−     стартова швидкість навчання  ;

−     зменшення швидкості навчання  .

Число нейронів ;  число ознак (входів нейронів) .

 

 

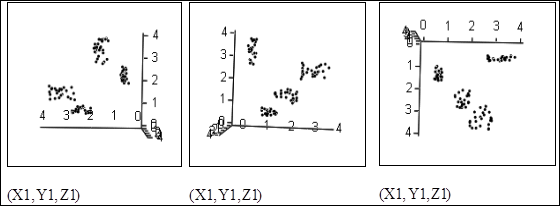
Рисунок 9.24 – Проекції в просторі перших трьох ознак

 

Три проекції в просторі перших трьох ознак

Задаємо номери нейронів для яких дивимось перехідні процеси:

 

;    ;   .

 

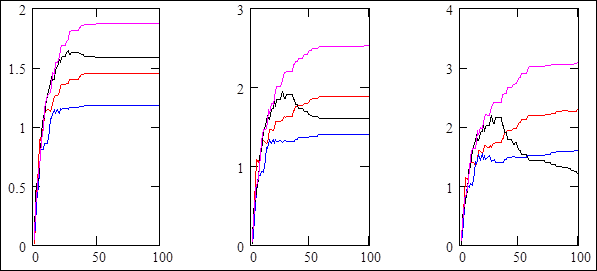
Рисунок 9.25 – Перехідні процеси навчання штучних нейронів

 

Зробимо анімацію, щоб подивитись еволюцію стану нейронів. Виразимо стан нейронів через системну змінну "фрейм". Далі все робимо згідно з інструкцією.

.

 

 

 

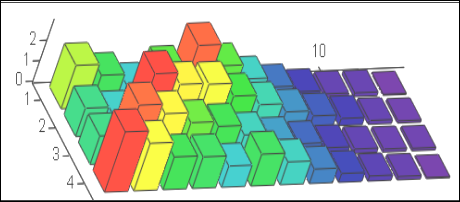
Рисунок 9.26 – Поточний стан процесу навчання нейроній мережі

 

Проаналізуємо, що ми власне отримали і до чого це можна застосувати.  Розглянули ряд задач адаптивного управління і побудували працюючі моделі адаптивних систем.

За статистикою і комп’ютерною пресою термін "інтелектуальний", застосований до програмних продуктів, у 90% випадків є просто рекламною прикрасою. З того, що входить у 10%:

-9% - програми на базі нейронних мереж, мурашиних, мишиних і генетичних алгоритмів, які застосовують для задач, які розв’язуються і без застосування  цієї термінології;

- 1%  - новаторські  роботи.

Однак це природна пропорція.

 

Контрольні питання

 

1. Запишіть рівняння для нелінійностей "зона нечутливості" та "обмеження".       

2. Як модіфікувати документ для дослідження впливу цих нелінійностей у вимірювачах -  координати, швидкості, прискорення.

3. Які методи і критерії для перевірки нелінійних САУ на стійкість ви знаєте?     

4. Наведіть приклади елементів САУ із а) зоною нечутливості, б) обмеженнм,  в) зоною нечутливості та обмеженнм.