---

РОЗДІЛ 9 СУЧАСНІ ТЕОРІЇ МОДЕЛЮВАННЯ ДОХІДНОСТІ ФІНАНСОВИХ АКТИВІВ

9.1 Модель Марковітца

Проблема формування і керування інвестиційним портфелем постала перед інвесторами давно. Своїми історичними коренями дана проблема з’явилася в середині ХХ століття. Американські вчені-економісти Марковітц і Шарп є творцями теоретичних концепцій формування і керування портфеля цінних паперів. Уперше модель оцінювання інвестиційного портфеля була розроблена Марковітцем.
Основна ідея моделі Марковітца полягає в тому, щоб статистично розглядати майбутній дохід, принесений фінансовим інструментом, як випадкову змінну, тобто доходи по окремих інвестиційних об'єктах випадково змінюються в деяких межах. Тоді, якщо якимось чином визначити по кожному інвестиційному об'єкту цілком певні імовірності настання, можна отримати розподіл ймовірностей одержання доходу по кожній альтернативі вкладення засобів. Для спрощення модель Марковітца передбачає, що доходи по альтернативах інвестування розподілені нормально [17, 19].
У 1952 р. Гаррі Марковітц опублікував фундаментальну роботу, що є основою підходу до інвестицій з погляду сучасної теорії формування портфеля. Підхід Марковітца починається з припущення, що інвестор у даний момент часу має конкретну суму грошей для інвестування. Ці гроші будуть інвестовані в певний проміжок часу, що називається періодом володіння (holding period). Наприкінці періоду володіння інвестор продає цінні папери, що були куплені на початку періоду, після чого або використовує отриманий прибуток на споживання, або реінвестує прибуток у різні цінні папери (або робить те й інше одночасно). Таким чином, підхід Марковітца може бути розглянутий як дискретний підхід, при якому початок періоду позначається t = 0, а кінець періоду позначається t = 1. У момент t = 0 інвестор повинний прийняти рішення про купівлю конкретних цінних паперів, що будуть знаходитися в його портфелі до моменту t = 1. Оскільки портфель являє собою набір різних цінних паперів, це рішення еквівалентне вибору оптимального портфеля з набору можливих портфелів. Тому подібну проблему часто називають проблемою вибору інвестиційного портфеля.
Приймаючи рішення в момент t = 0, інвестор має мати на увазі, що прибутковість цінних паперів (і, таким чином, прибутковість портфеля) у майбутній період володіння невідома. Однак інвестор може оцінити очікувану (або середню) прибутковість (expected returns) різних цінних паперів, ґрунтуючись на деяких припущеннях, а потім інвестувати засоби в папір з найбільш очікуваною прибутковістю. Марковітц відзначає, що це буде в загальному нерозумним рішенням, тому що типовий інвестор хоча і бажає, щоб «прибутковість була високою», але одночасно хоче, щоб «прибутковість була б настільки визначеною, наскільки це можливо». Це означає, що інвестор, прагнучи одночасно максимізувати очікувану прибутковість і мінімізувати невизначеність (тобто, ризик (risk)), має дві суперечні одна одній цілі, які мають бути збалансовані при прийнятті рішень про купівлю в момент t = 0. Підхід Марковітца до прийняття рішення дає можливість адекватно врахувати обидві ці мети.
За моделлю Марковітца визначаються показники, що характеризують обсяг інвестицій і ризик, що дозволяє порівнювати між собою різні альтернативи вкладення капіталу з точки зору поставлених цілей і, тим самим, створити масштаб для оцінювання різних комбінацій.
Як масштаб очікуваного доходу з ряду можливих доходів на практиці використовують найбільш ймовірне значення, що у випадку нормального розподілу збігається з математичним сподіванням.
Нехай формується портфель з n цінних паперів. Очікуване значення доходу за i-тим цінним папером Ei розраховується як середнє арифметичне з окремих можливих доходів Ri з вагами Рij, приписаними їм ймовірностями настання:

де n – кількість оцінок доходу для кожного цінного паперу.

Для вимірювання ризику служать показники розсіювання, тому, чим більше розкид величин можливих доходів, тим більше небезпека, що очікуваний дохід не буде отримано. Таким чином, ризик виражається відхиленням значень доходів від найбільш ймовірного значення. Мірою розсіювання є середньоквадратичне відхилення і, чим більше це значення, тим більший ризик.
У моделі Марковітца для вимірювання ризику замість середньоквадратичного відхилення використовується дисперсія Di, що дорівнює квадрату , тому що цей показник має переваги з техніки розрахунків.
Марковітц розробив дуже важливе для сучасної теорії портфеля цінних паперів положення, що говорить: сукупний ризик портфеля можна розкласти на дві складові частини. З одного боку, це так званий систематичний ризик, який не можна виключити, і який впливає на всі цінні папери практично однаковою мірою. З іншого боку – специфічний ризик для кожного конкретного паперу, якого можна уникнути за допомогою керування портфелем ЦП. При цьому сума вкладених засобів по всіх об'єктах має дорівнювати загальному обсягу інвестиційних вкладень (наприклад, частина засобів на банківському рахунку вводиться в модель як інвестиція з нульовим ризиком), тобто сума відносних часток Хі в загальному обсязі має дорівнювати одиниці.
Проблема полягає в чисельному визначенні відносних часток акцій і облігацій у портфелі (значень Хі), що найбільш вигідні для власника. Марковітц обмежує розв’язання моделі тим, що з усієї безлічі «припустимих» портфелів, тобто тих, що задовольняють обмеження, необхідно виділити ті, які ризикованіші за інші. Це портфелі, що містять при однаковому доході більший ризик (дисперсію) порівняно з іншими, або портфелі, що приносять менший дохід при однаковому рівні ризику.
За допомогою розробленого Марковітцем методу критичних ліній можна виділити безперспективні портфелі, що не задовольняють обмеження. Тим самим залишаються тільки ефективні портфелі, тобто портфелі, що містять мінімальний ризик при заданому доході або ті, які приносять максимально можливий дохід при заданому максимальному рівні ризику, на який може піти інвестор.
Даний факт має дуже велике значення в сучасній теорії портфелів цінних паперів. Відібрані в такий спосіб портфелі складають список, що містить зведення про процентний склад портфеля з окремих ланцюгових паперів, а також про дохід і ризик портфелів. Вибір конкретного портфеля залежить від максимального ризику, на який готовий піти інвестор.
З методологічної точки зору модель Марковітца можна визначити як практично-нормативну, що, звичайно, не означає нав'язування інвесторові певного стилю поводження на ринку цінних паперів. Задача моделі полягає в тому, щоб показати, як поставлені цілі досягаються на практиці.
Приклад розрахунку частин активів в портфелі за моделлю Марковітца.
Позначимо дисперсію портфеля .Тоді

де xi  – частка i -го цінного паперу в портфелі; xj  – доля j -го цінного паперу в портфелі;  – коваріація даних паперів.
Обмеження:

 середня дохідність портфеля:
де xi  – частка i -го цінного паперу в портфелі;  – очікувана дохідність i -го цінного паперу.

Для розв’язання цієї задачі необхідно сформувати функцію Лагранжа:

де ,  – множники Лагранжа.
Портфель, який зменшує ризик (зводить його до мінімуму), визначається рішеннями системи:

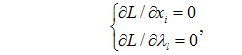
l = 1, 2.
Перепишемо нашу задачу для випадку, коли i, j = 1, 2, 3:

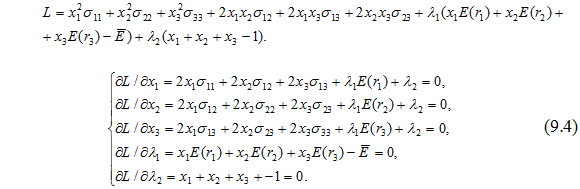
Подамо систему в матричному вигляді:

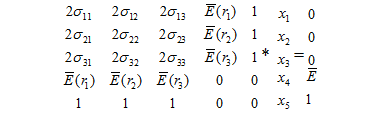
Якщо позначити матрицю через Н, вектор – через А та вектор в правій частині  – через  G, то отримаємо рівняння:

                                                    H×A=G,                                              (9.5)
A=H-1×G .

Приклад.  Є три акції, запишемо їх характеристики у вигляді такої таблиці:

Номер акції (i)	E(ri)
1	0,06	0,35	12 = -0,1
2	0,09	0,42	23 = 0,42
3	0,18	0,75	13 = 0,30

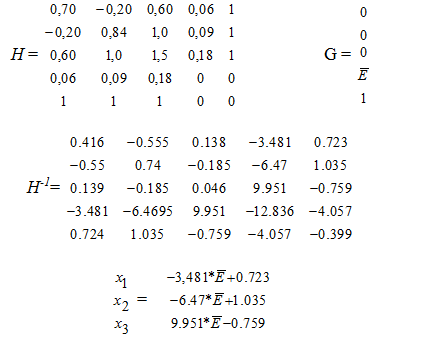
Якщо ми уявимо, що інвестор захоче отримати прибуток Е=12%, то отримаємо: х1 = 0,305; х2 = 0,259; х3 = 0,435; ∑ хі = 1.

9.2 Модель CAPM

Основні положення. Основним здобутком CAPM (The Capital Asset Pricing Model) є процедура визначення узгодженого очікуваного доходу УОД (consensus expected return). Використання узгодженого очікуваного доходу (УОД) дозволяє отримати певний стандарт для визначення та порівняння очікуваного доходу при розрахунках за іншими методиками [19].
Як наслідок, рішення стосовно активного менеджменту портфеля активів може бути прийняте на основі розрахунків різниці між очікуваним доходом  та його узгодженим (справедливим) значенням.
Основними положеннями CAPM є:

• дохід, отриманий за певним активом може бути виділений в систематичний (ринковий) компонент та залишковий (residual) компонент;
• CAPM стверджує, що очікуване значення залишкового компоненту доходу дорівнює нулю;
• CAPM є легкою для розуміння та реалізації в менеджменті;
• в CAPM реалізовано принцип ефективності ринку;
• CAPM доводить, що пасивний менеджмент є альтернативою активному менеджменту як менш ризикований;
• CAPМ є ефективним способом визначення УОД і, як наслідок, активний менеджер може використовувати розрахунки УОД згідно з CAPM для оцінювання ефективності власних результатів (beat the market!);
• інструментарій CAPM дозволяє прогнозувати очікуваний дохід, але не ризик.

Теорія СAPM не є єдиним способом прогнозування очікуваного доходу, але дійсно є найкращою. Альтернативним способом прогнозування УОД є використання усередненого історичного доходу, тобто середній дохід по активу за певний період часу (1 рік, 10 років тощо).
Недоліками такого підходу є :

• історичний дохід містить значну складову похибки моделі. Якщо річне стандартне відхилення σ, тоді стандартна похибка очікуваного річного доходу дорівнює σ/√Y , де  Y – кількість років. Таким чином, якщо типова волатильність активу ≈ 35%, то стандартна похибка буде  ≈ 16% після 5 років досліджень;
• перспективи будь-якого активу змінюють в часі. З’являються нові акції та зникають старі. Окрім цього, самі активи є мінливими: прибутки компанії, структура капіталу та волатильність акції змінюється.

    Іншою альтернативою для розрахунку очікуваних доходів є Теорія цінового арбітражу (The Arbitrage Pricing Theory). Однак АРТ не є ефективним інструментом для оцінки УОД
Очевидною перевагою CAPM є її використання при формуванні портфелів з оптимальним співвідношенням:

                                              середній дохід              
                                   діапазон зміни портфеля.

Згідно з CAPM оптимальний портфель складається з „ринку” та безризикових активів у співвідношенні, що визначається вимогами до загального ризику. Тобто оптимальний портфель буде відрізнятися від портфеля, що складається з „ринку” та безризикових активів лише тоді, коли прогнозований дохід портфеля відрізняється від УОД, розрахованого за CAPM.
Виділення доходу в систематичну (ринкову) та несистематичну (залишкову) складові.
Існують два базових постулати CAPM:

• наявність ринкового портфеля М;
• наявність коефіцієнтного бета β, що встановлює залежність між будь-яким активом в портфелі та ринком.

На практиці під ринковим портфелем  розуміють індекс, що включає (з відповідними ваговими коефіцієнтами) індекси провідних бірж акцій: NYSE, FTA, TOPEX тощо.
Розглянемо деякий портфель Р з надлишковим доходом та ринковий портфель з надлишковим доходом.

Надлишковий дохід дорівнює різниці між загальним доходом портфеля та загальним доходом безризикового портфеля за той самий період. Визначимо β портфеля Р як:

Зауважимо, що ринковий портфель має β = 1, а безринковий актив має β = 0.
Визначення β походить з рівняння лінійної регресії надлишкових доходів портфеля за періоди  t = 1, 2… відносно надлишкових доходів ринкового портфелю за ті ж самі періоди:

(9.6)

за умови, що(історичний коефіцієнтний альфа).

Використання β дозволяє в надлишковому доході будь-якого портфеля виділити ринковий компонент  та залишковий компонент:

             (9.7)

Крім того, оскільки залишковий дохід      є некорельованим з ринковим доходом     , середнє квадратичне СКВ портфеля:

(9.8)

де       – середнє квадратичне залишкового доходу портфеля.
Висновки. CAPM стверджує, що очікуваний залишковий дохід по всіх акціях будь-якого портфеля дорівнює нулю:

   

тобто очікуваний надлишковий дохід портфелявизначається повністю надлишковим очікуваним доходом від ринкута значенням β портфеля:

Іншими словами, CAPM стверджує, що усі інвестори мають однакові сподівання, та їх дохід є пропорційним тому ризику, який вони приймають на себе!
Зауважимо, дійсно, якщо підсумувати (з відповідними ваговими коефіцієнтами) доходи по всіх акціях, що входять в ринок, ми отримаємо дохід ринку, а сума залишкових доходів буде дорівнювати нулю. Ризику впливу ринку уникнути неможливо. Ризику, пов'язаного з індивідуальним ризиком окремого активу, можна уникнути.
CAPM стверджує, що інвестори, які мають портфелі, що відрізняються від ринкових, не отримують додаткового очікуваного доходу, хоча приймають додатковий ризик.
Прогнозування β та очікуваного ринкового доходу. Аналіз попередніх рівнянь підводить до ідеї, що точність прогнозування очікуваного доходу згідно з CAPM ідентична точності прогнозування β. Найпростішим способом прогнозування β є метод аналізу історичних рядів даних.
Основні властивості ризику:

1. ризик є стандартним відхиленням доходу;
2. ризик не є адитивним;
3. більшість інвесторів піклується про активний та залишковий ризик  але не про загальний ризик ;
4. активний ризик, в основному, залежить від розміру активної позиції, а не від розміру позиції, яка ідентична ринку;
5. вартість ризику пропорційна варіативності портфеля;
6. основне призначення моделей, що працюють з ризиком, –  це визначення джерел виникнення ризику та намагання виділення ризику в окремі компоненти.

Всі визначення ризику походять з ймовірного розподілу можливих доходів. Такий розподіл описує ймовірності, що дохід потрапить у діапазон 1-1.01, 1.01-1.02 та інші (рис. 9.1).

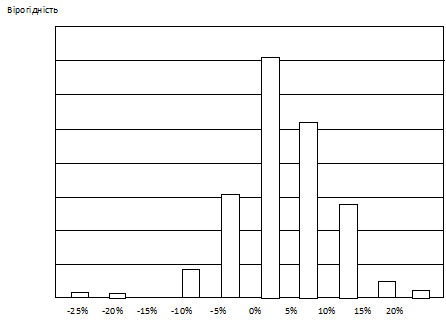
Рисунок 9.1 – Ймовірність розподілу доходів портфеля

Згідно з цим розподілом 26% місячних доходів припадають на діапазон між 2,5 та 7,5%.
Виходячи з припущення, що закон розподілу доходів є нормальним усі параметри ризику можуть бути розраховані на основі мат. сподівання  та СКВ.         В інвестиційній практиці СКВ часто розглядається як волатильність.
На рис. 9.1 σ = 6,3% та М = 1,6%. Виходячи з припущення про норм. закон розподілу 2/3 доходів припадають на 6,3%. Фактично 73% доходів Magellan Fund (рис 9.1) припадають на діапазон – 4,7 та 7,9%.
Зменшення σ призводить до звуження діапазону, на який припадає більшість доходів. Тобто σ визначає ступінь невизначеності доходів. Вперше σ була запропонована для визначення ризику Гаррі Марковітцем, з того часу використовується інституціональними інвесторами.
Ще одним параметром для опису ризику є напівваріативність, що розраховується як доходи, менші за математичне сподівання. Але у випадку, коли доходи розподілені симетрично, напівваріативнісь пропорційна σ  та не містить нової інформації. А якщо доходи розподілені несиметрично, розрахунки цього параметра є проблемою, тому що асиметричні доходи не є стабільними у часі. До того ж  використання лише половини даних призводить до втрати статистичної достовірності.
Третій спосіб визначення ризику має назву Shortfall Probability та являє собою ймовірність спаду доходу нижче заданого рівня. Так ймовірність спаду місячного доходу Magellan Fund нижче 10% дорівнює 3,4%.
Використання стандартного відхилення в CAPM. Однією з цікавих властивостей σ є той факт, що σ не має «портфельної» властивості. Тобто σ портфеля не є середньозваженим СКВ компонентів [19].

Якщо акції 1 та 2 мають кореляцію Р12 , та портфель складається з 50% акцій 1 та 2, то σр можна визначити:

або  

якщо акції 1 та 2 повністю  корельовані.
Якщо розглядати портфель з N акцій з ризиком σ та некорельованими доходами, ризик портфеля, що складається з рівнозважених акцій:

Очевидно, що ризик портфеля в          разів менший за середній ризик.
У випадку однакової кореляції P між усіма парами акцій у портфелі, ризик портфеля :

Якщо портфель складається з дуже великої кількості акцій:

Залишковий ризик та дохід Information Ratio (IR). Визначення αр. Розрізняють два види αр: Ex Ante, що прогнозує залишковий дохід, та Ex Post – середнє значення отриманих залишкових доходів (історичне значення). Параметр αр, як і β походить з рівняння лінійної регресії, яке дозволяє виділити загальний дохід портфеля в компонент, ідентичний ринку, а також залишковий компонент. 

В рівнянні

залишковий компонент є:

де αр  – середній залишковий дохід.
Параметр αр  має «портфельну» властивість, тобто α окремих акцій, що входять до портфеля, є адитивними.
Таким чином, якщо ми маємо портфель з двох акцій: α1 та α2 відповідно, а кількість акцій в портфелі hр (1) та hр (2) відповідно, то загальна αр :

За аналогією з αр розрізняють Ex Post Information Ratio та Ex Ante Information Ratio (IR). Information Ratio є дуже поширеним критерієм оцінки збалансованості портфеля з точки зору співвідношення дохід-ризик.

IR являє собою відношення залишкового ризику, розрахованого за певну кількість років

де  ωp  – залишковий ризик.
Дану модель необхідно використовувати у таких випадках.
1. Якщо ринок буде зростати з високою імовірністю:
• варто купувати папери з високими додатними значеннями β;
• і/або продавати папери з високими від’ємними β.
2. Якщо ринок буде спадати з високою імовірністю:
• купівля паперів з низькими додатними значеннями β;
• і/або короткий продаж паперів з низькими від’ємними значеннями β.
3. Середня імовірність зростання:
• купівля паперів з низькими додатними значеннями β;
• і/або продаж активів з низькими від’ємними значеннями β;
• або відкриття однієї довгої позиції за акцією з високим додатним β і ще однієї – за акцією з низьким від’ємним коефіцієнтом;
• або відкриття довгої позиції за акцією з високим додатним значенням β і короткої – за акцією з низьким;
• або відкриття однієї короткої позиції за акцією з високим від’ємним значенням β і ще однієї – за акцією з низьким;
• або відкриття однієї короткої позиції за акціями з високим від’ємним β і ще однієї – за акцією з низьким додатним β.
4. Очікується спад з невисокою імовірністю:
• покупка паперів з низькими додатними β;
• і/або короткий продаж паперів з низькими додатними значеннями β;
 відкриття однієї довгої позиції за акцією з високим від’ємним β і ще однієї – за акцією з низьким додатним β;
• або відкриття довгої позиції за акцією з високим від’ємним β і короткої – за акцією з низьким;
• відкриття однієї короткої позиції за акцією з високим додатним значенням β і однієї – за акцією з низьким, або відкриття однієї короткої позиції за акцією з високим додатним бета й однієї – за акцією з низьким від’ємним β .
Недоліки САРМ: вважають, що основним недоліком методу є спосіб розрахунку додаткової премії за ризик, на яку прибутковість акцій перевищує прибутковість безризикових цінних паперів. У таких розрахунках у САРМ застосовується коефіцієнтний бета β, що показує, наскільки зміни ціни даного активу відповідають змінам цін інших активів, тобто взаємозв'язок ціни акцій окремої компанії і ринкової прибутковості.  Ці розрахунки корисні при виборі активів для диверсифікації портфеля. Ціна активу може значно коливатися, але це не буде становити великого ризику для диверсифікованого портфеля, якщо тільки ця ціна не буде змінюватися одночасно з цінами інших активів. Однак за допомогою моделі САРМ неможливо оцінити загальний ризик інвестицій. За словами експертів, це є істотним недоліком для корпоративних менеджерів, яким платять за те, щоб активи компанії приносили доходи набагато вищі середніх.
Застосування моделі САРМ на практиці нерідко дає дивні результати. Наприклад, фірма Home Depot (штаб-квартира в Атланті), що займається ремонтом житла, установила в 1995 році β-коефіцієнт рівним 1,6. Ця цифра означала, що акції компанії більше, ніж на половину ризикованіші порівняно із середнім ринковим показником і більше, ніж удвічі ризикованіші  порівняно з акціями її невеликого мічиганського конкурента Wolohan Lumber, у якого β-коефіцієнт складав у той час 0,75.
Ризики розглядалися винятково на основі β-коефіцієнта, при цьому не бралася до уваги норма прибутку Home Depot, яка стабільно збільшувалася, у той час як у Wolohan Lumber вона знижувалася. Через три роки в обох компаніях β-коефіцієнт склав 0,7. Які б не були переваги цього коефіцієнта як історично сформованої міри ризику, цілком покладатися на нього при побудові прогнозів на майбутнє не можна.
Через ненадійність β-коефіцієнта багато компаній не застосовують модель САРМ і довільно встановлюють мінімально прийнятні для себе значення прибутковості інвестицій. Один з колишніх керівників фінансової служби бостонського відділення компанії Gillette говорить, що донедавна ця фірма завжди встановлювала мінімально припустиму ставку прибутковості інвестицій на рівні 20% незалежно від конкретного проекту.

Компанії, що застосовують β -коефіцієнт, часто «підганяють» під нього свої оцінки ставок прибутковості. Вони також нерідко коректують ставки, розраховані за моделлю САРМ, для того, щоб відбити такі фактори, як розмір компанії, співвідношення між акціонерним і позиковим капіталом, а також специфіку конкретних інвестицій.

9.3 Теорія арбітражного ціноутворення

Існує таке поняття як арбітраж. Це фінансова операція. Вона проводиться для одержання прибутку від перепродажу фінансів з урахуванням грошової різниці в межах одного ринку, але в різний час або на інших ринках [19].
Саме поняття "арбітраж" припускає одержання гарантованого, безризикового прибутку від гри на ринку. Прикладом арбітражу може служити така ситуація, коли акції однієї компанії котируються на різних торговельних площадках, і поточна ринкова вартість однієї і тієї ж акції на них різна. Тоді очевидна така послідовність дій: потрібно здійснити короткий продаж (продаж цінних паперів, узятих у борг) певної кількості акцій на тій площадці, де акції коштують дорожче, і купити ту ж кількість акцій на іншій площадці, де вони коштують дешевше. Тепер уявіть, що така можливість дійсно має місце. Оскільки учасників торгів на фондовому ринку багато, навряд чи варто сподіватися, що цю можливість більше ніхто не помітив, – обов'язково помітять і почнуть використовувати. Але "несподіване" збільшення попиту на одній торговельній площадці, де акції коштують дешевше, і пропозиції на іншій, де акції дорожчі, неминуче приведуть до вирівнювання цін: підвищений попит стимулює підвищення ціни, а підвищена пропозиція – її зниження. Описана ситуація являє собою приклад найпростішого арбітражу.
Розрізняють арбітраж простий, здійснюваний із двома валютами, і складний, якщо в угоді беруть участь три і більше валют.
Залежно від способу формування прибутку від проведеної угоди виділяють кілька видів арбітражу:

• тимчасовий –це найбільш розповсюджений вид арбітражу на ринку Forex, що заснований на різниці курсів валютних пар у різний час;
• кросовий. Він же складний валютний арбітраж. Виникає в тому випадку, коли відбувається одночасна синхронна зміна курсів у двох парах, наприклад, USDJPY і EURUSD. Такі кроси-дисбаланси присутні на ринку постійно. При одночасовому здійсненні подібної угоди ризик її мінімальний;
• міжбіржовий.  Виникає у випадку, коли ставка робиться на різницю курсів валют на різних валютних біржах. У сучасних умовах, коли котирування валют практично однакові, проведення подібних арбітражних угод доволі складне.

АРТ є цікавою та потужною  альтернативою САРМ для прогнозування очікуваного доходу. Вона виникла як подальший розвиток моделі САРМ наприкінці 1970-х р. В основі теорії лежать два положення:

• у стані загальної економічної рівноваги на всіх конкурентних ринках, включаючи ринок цінних паперів, установлюються ціни, що виключають можливість арбітражу;
• очікувана величина і ризик доходу цінного папера визначаються не одним, як у моделі САРМ (коливаннями прибутковості ринкового портфеля), а декількома факторами (коливаннями ВВП, темпу інфляції, обмінного курсу національної валюти й ін.).

Теорія арбітражного ціноутворення (АРТ) була запропонована професором Єльського університету С. Россом у 1976 р. і є альтернативною САРМ моделлю загальної рівноваги на фінансовому ринку. Головним припущенням теорії є те, що кожен інвестор прагне використовувати можливість збільшення прибутковості свого портфеля без збільшення ризику.
Модель APT у загальному виді виглядає як:

де  – середня прибутковість i-го активу,  – прибутковість безризикового активу,   – впливні фактори ризику.
Побудова моделі пов'язана з певним суб'єктивізмом: які фактори вибрати та яким має бути критерій включення фактора в підсумкову модель інвестор вирішує самостійно. Автором був запропонований алгоритм побудови моделі APT, у якій суб'єктивний фактор зведений до мінімуму.
Універсальний алгоритм побудови включає 7 основних етапів:
1. Визначення всієї сукупності факторів, які можливо впливають на ціну, і поділ їх методом агрегування на групи. Основними групами, на думку автора, є: фінансові показники фірми, макроекономічні індикатори країни, галузеві індикатори, світові фондові індекси, сировинні ціни, політичні і корпоративні події і т. д.;
2. Виділення для підприємства, що досліджується, аналогів на основі галузевої належності, ліквідності акцій, капіталізації і т. д.;
3. Аналіз впливу кожної з груп на ціну активу, що досліджується,  і ціни аналогів;
4. Сформовані нові групи ранжують за рівнем детермінації R2 побудованих моделей,  який впливає на кількість змінних у даних групах.
Ранжування груп здійснюється за  трьома  рівнями:

• перший відповідає: 0,7 = < R2 < 1 (установимо, РГ = 1);
• другий відповідає: 0,5 =< R2 < 0,7 (РГ = 2/3);
• третій відповідає: 0 < R2 < 0,5 (РГ = 1/3), де РГ – коефіцієнт рівня групи;

5. Визначити кількість змінних у кожній із груп.
Кількість змінних у кінцевій моделі не повинна перевищувати значення N:

де G– загальна кількість змінних у всіх групах; – початкова кількість змінних у групі i.
6. За критерієм значущості вибрати змінні таким чином.
Критерій 1 –  критерій  значущості для змінних вибирається як імовірність прийняття значення змінною нуля та має бути меншим 10%.
Критерій 2 – критерій включення змінної в групу, що бере участь у підсумковій багатофакторній моделі, визначається як значущість змінної хоча б у 2-х з побудованих багатофакторних моделях (активу, що досліджується, й аналогів). Якщо ж кількість змінних задовільна, а Критерій 2 не збігається з визначеною кількістю змінних у пункті 5, то використовується Критерій 3;
Критерій 3 – критерій включення в групу тієї змінної, в якої сума ймовірностей прийняття змінною нуля для досліджуваної компанії й аналогів найменша.
7. Будується багатофакторна модель, використовуючи сформовані групи.
Переваги даної моделі такі:

1. АРТ є моделлю очікуваних доходів ;
2. успішність застосування  АРТ є скоріше мистецтвом, ніж наукою ;
3. АРТ вказує та допомагає менеджеру виявити зв'язок між факторами та очікуваним доходом;
4. фактори, що використовуються в АРТ, можуть бути визначені в широкий спосіб. Такими факторами можуть бути фундаментальні, технічні та  макроекономічні фактори;
5. гнучкість АРТ  не дозволяє використовувати її як модель для оцінювання узгодженого  очікуваного доходу, але є прийнятною моделлю для оцінювання  очікуваного доходу  портфеля певного менеджера;
6. АРТ є джерелом інформації для активного менеджера при формуванні його особистих управлінських рішень.

Основним постулатом АРТ є той факт, що надлишковий очікуваний дохід від акції визначається впливом факторів, які беруться до розгляду. Кожний з факторів має свою вагу (прогноз фактора) і таким чином загальний очікуваний надлишковий дохід за акцією являє собою суму добутків впливу кожного фактора k на акцію n на їх коефіцієнти впливу на акцію bk(factor exposure).

де  Xn,k   – вплив фактора k на акцію n.
На практиці  Xn,k є відомими до початку розрахунку rp. Дохід, що внесений фактором приймається до уваги наприкінці періоду спостереження або протягом нього; un  – специфічний дохід, який може приносити акція, та який не можна пояснити з точки зору переліку факторів, взятих до уваги.
Основна ідея теорії APT полягає в тому, що повний перелік правильних факторів впливу на акцію при розрахунку очікуваного доходу існує. Але теорія не відповідає на питання, як визначити ці фактори. Якщо застосувати САРМ до APT ми одержимо лише один фактор k = 1, причому вплив цього фактора на акцію є ідентичним β. Тобто  .
Очікуваний дохід, пов'язаний з цим фактором, є: , де  – очікуваний дохід від ринку.
Інше практичне застосування АРТ полягає у такому. Спочатку потрібно розділити акції за належністю до промислових секторів та  виділити 4 інші атрибути компанії, наприклад :

1. прогноз росту прибутків компанії ;
2.  β  акції відносно індексу урядових облігацій ;
3. розмір компанії (натуральний логарифм від ринкової капіталізації компанії) ;
4. дохід, що виплачує компанія на одну звичайну акцію (ROE).

Перелічені фактори включають в себе прогноз зростання прибутків, макроекономічні характеристики, характеристики компанії та фундаментальні дані по акціях.
Значно простіше застосовувати АРТ модель для різноманітних факторів, якщо використовувати їх у стандартизованому вигляді.  Цього можна досягти шляхом віднімання середнього ринкового значення від певного фактора і ділення на σ фактора.
Приклад 1. Ціни акцій A, B, C і D, що обертаються на ринку,рівні 77; 85; 110 і 75 у.о. Очікуваний від них через рік дохід залежить від того, чи збережеться існуючий обмінний курс національної валюти, підвищиться він або знизиться (табл. 9.1).
При поточних цінах у розглянутому прикладі можливий арбітраж. Складемо портфель із трьох перших акцій, що забезпечує такий же очікуваний дохід, який має акція D. У такий портфель потрібно включити 2,43 акцій A; 0,22 акцій B і -1,24 акцій C (тобто продати взяту на час цю кількість акцій C).

Таблиця 9.1 – Очікувана прибутковість акцій

Акція	Поточна ціна, у.о.	Очікуваний доход, якщо обмінний курс, у.о.
		знизиться	не зміниться	збільшиться
A	77	60	75	90
B	85	100	75	75
C	110	95	120	105
D	75	50	50	105

Структура такого портфеля знаходиться із системи рівнянь:

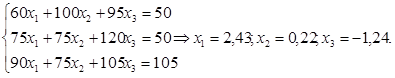
Його ціна буде: 77×2,43 + 85×0,22 - 110×1,24 = 69,4. Отже, продавши акцію D і купивши зазначений портфель, одержимо 75 - 69,4 = 5,6 у.о. доходу. Із збільшенням пропозиції акцій D і попиту на інші акції на ринку акцій установиться система цін, що виключає одержання арбітражного доходу. Однією з таких систем може бути: z = 77; z = 85; z = 110; z = 69,4.
Очікувану прибутковість окремої акції в концепції АРТ розраховують за формулою:

де n – число факторів ризику; βi – реакція (чутливість) очікуваної прибутковості акції на зміну значення i-го фактора ризику; λ0 – прибутковість безризикових вкладень; λi – премія за ризик, обумовлена i-м фактором.
Приклад 2. На ринку обертаються три види акцій – A, B і C. Їхня очікувана прибутковість і коефіцієнти її реакції на зміни темпу росту ВВП (β1) і темпу інфляції (β2) подано в табл. 9.2.
У заданих умовах не буде можливості отримання доходу від арбітражу, якщо λ1 = 3,75; λ2 = 2,5; λ3 = 8,75. Їхні значення знаходяться з такої системи рівнянь:

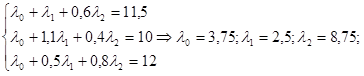
Таблиця 9.2 – Дані по акціях

Акція		Β1	β2
А	11,5	1,0	0,6
B	10,0	1,1	0,4
C	12,0	0,5	0,8

Припустимо, що фірма D вирішує вийти на ринок капіталу, пропонуючи свої акції з очікуваною прибутковістю r = 11 при βD1 = 0,75 і βD2 = 0,45. З акцій A, B і C можна скласти портфель, що має таку ж чутливість до факторів ризику, яку має акція D. Візьмемо, наприклад, 0,4 акції A, 0,257 акції B і 0,134 акції C. Коефіцієнт чутливості цього портфеля до зміни темпу зростання ВВП дорівнює

0,4×1 + 0,257×1,1 + 0,134×0,5 = 0,75,

а до зміни темпу інфляції

0,4×0,6 + 0,257×0,4 + 0,134×0,8 = 0,45,

але його очікувана прибутковість нижче, ніж в акції фірми D:

0,4×11,5 + 0,257×10 + 0,134×12 = 8,78.

Тому наявна можливість арбітражу. Здійснимо «порожній продаж» складеного портфеля і на виручені гроші купимо акції фірми D. Результати цієї операції в розрахунку на 1000 у.о. подано в табл. 9.3.

Таблиця 9.3 – Результати операції «порожній продаж»

Вид операції	t0	t1	1	2
Продаж портфеля А,В,С	+1000	-1087,8	-0,75	-0,45
Купівля акції D	-1000	+1100	+0,75	+0,45
Разом	0	+122,2	0	0

Використання виявленої можливості виграшу на описаній операції приведе до зниження цін акцій, що входять у портфель, і підвищення ціни акції фірми D. Коли можливості арбітражу будуть вичерпані, на ринку акцій знову установиться рівновага і ціна акції D набуде свого рівноважного значення.
Порівнюючи концепції АРТ і САРМ, можна відзначити, що теорія арбітражного ціноутворення може бути подана в багатоперіодному варіанті, у ній не передбачається як обов'язкова умова існування фінансового інструмента з безризиковою прибутковістю і для її застосування не потрібно обчислювати середнє очікуване значення доходу від цінних паперів і його варіацію. З іншого боку, САРМ являє собою модель визначення всієї системи рівноважних цін цінних паперів, що обертаються на ринку, у той час як АРТ пояснює формування рівноважної ціни на окрему, що знову з'являється на ринку, акції.
У класичній моделі САРМ враховувався тільки один фактор, і актив характеризувався двома параметрами – коефіцієнтним бета, що характеризує ризик, пов'язаний з цим фактором, і середньою залишковою прибутковістю Е, що відповідає за специфічний ризик, тобто ризик, який не пояснюється впливом обраного фактора. У моделі АРТ з'явилася можливість враховувати кілька факторів.
Тепер актив характеризується набором показників "бета", кожний з яких являє собою чутливість активу до визначеного фактора і характеризує систематичний ризик, пов'язаний із впливом саме цього фактора, і, як і раніше, залишковою прибутковістю Е. Тільки тепер величина специфічного (непоясненого факторами) ризику стала набагато меншою.
Але перехід від однофакторної моделі САРМ до багатофакторного АРТ не тільки дає переваги, але і ставить нові проблеми, що раніше не виникали [19]. Найважчою проблемою в моделі теорії арбітражного ціноутворення є визначення факторів, що впливають на очікувану ставку доходу за цінним папером, та їх кількість. У теорії С. Росса ці  фактори не позначені. В американській літературі висловлюється думка, що для кожної галузі господарства застосовні специфічні фактори.

Питання для самоперевірки

1. Основна ідея моделі Марковітца.
2. Як розраховується прибутковість за моделлю Марковітца?
3. Що використовується для опису ризику в моделі Марковітца?
4. Назвіть основні положення моделі САРМ.
5. Назвіть недоліки та переваги застосування моделі САРМ.
6. Які основні властивості ризику в моделі САРМ?
7. Як використовується середньоквадратичне відхилення для розрахунку альфа та бета в моделі САРМ?
8. Коли доцільно використовувати модель САРМ?
9. Що таке арбітраж та які його види Ви знаєте?
10. В чому основна ідея теорії АРТ? Загальний вигляд моделі АРТ.
11. Назвіть етапи побудови моделі АРТ.
12. Яка різниця між теоріями САМР та АРТ?
13. Яка основна проблема у теорії АРТ?

---