РОЗДІЛ 8 ДИВЕРСИФІКАЦІЯ ПОРТФЕЛЯ ЦІННИХ ПАПЕРІВ
8.1 Диверсифікація портфеля
Диверсифікація (diversification) – розподіл інвестиційного фонду між цінними паперами з різними ризиками, дохідностями і кореляціями, з метою мінімізації несистематичного ризику.
Щоб проілюструвати ідею диверсифікації розглянемо два цінні папери A та B з однаковою очікуваною прибутковістю E(A) = E(B) і однаковим рівнем ризику, що характеризується дисперсією прибутковості D(A) = D(B) [18, 19].
Виберемо з безлічі портфелів, що містять тільки цінні папери A і B, оптимальний портфель Р, виходячи із співвідношення очікуваної прибутковості і рівня ризику, що характеризується дисперсією прибутковості портфеля.
В даному випадку, вибір оптимального портфеля еквівалентний вибору частин Wa та Wb цінних паперів A і B в загальній вартості портфеля на початковий момент інвестиції, крім того Wa + Wb = 1. Відмітимо, що очікувана прибутковість такого портфеля постійна і дорівнює очікуваній прибутковості по кожному з цінних паперів, тобто:
Таким чином, оптимальний портфель слід вибирати з умови мінімізації дисперсії прибутковості портфеля.
Для обчислення дисперсії портфеля необхідно знати значення коефіцієнта коваріації цінних паперів A і B – Cov(A,B) або коефіцієнта кореляції, в даному випадку – Corr(A, B) = Cov(A, B)/D(A).
Тоді дисперсія всього портфеля D(P) буде розраховуватися таким чином:
Оскільки коефіцієнт кореляції, зокрема Corr(A, B), знаходиться в межах від -1 до 1 включно, тому дисперсія портфеля D(P), що включає цінні папери A і B в будь-якій пропорції, у будь-якому випадку не перевершує дисперсію D(A) або D(B) цінного паперу А (або B).
У разі, коли Corr(A, B) = 1 (наприклад, у разі, коли прибутковість цінного паперу A завжди збігається з прибутковістю цінного паперу B), як і природно було чекати D(P) = D(A) незалежно від вибору Wa, Wb.
У разі, коли Corr(A, B) < 1, для додатних значень Wa і Wb (таких, що Wa+Wb =1) дисперсія прибутковості портфеля D(P) буде строго менше дисперсії прибутковості по кожному з цінних паперів, що входять в портфель D(A) (або D(B)), причому мінімум D(P) = D(A)×(1 + Corr(A, B))/2 досягатиметься для Wa = Wb = 1/2 (дані значення максимізували добуток Wa×Wb за наявності обмеження Wa + Wb = 1).
Таким чином, у разі, коли Corr(A, B) < 1, включивши в портфель P цінні папери A і B в рівній пропорції, отримаємо портфель з тією ж прибутковістю E(P ) = E(A) = E(B), що і у разі інвестування в один цінний папір A (або B). Проте дисперсія прибутковості D(P), а також і ризик портфеля, буде строго менше дисперсії прибутковості цінного паперу A (B). Більш того, у разі, коли Corr(A, B) = -1, оптимальний портфель матиме нульову дисперсію – це означає, що вірогідність отримати прибутковість, відмінну від очікуваної, рівна нулю – безризикова інвестиція.
Таким чином, ефективна диверсифікація передбачає об'єднання цінних паперів з коефіцієнтом кореляції менше одиниці без принесення в жертву доходу по портфелю. Загалом, чим нижчий коефіцієнт кореляції цінних паперів, що входять в портфель, тим менш ризикованим буде портфель.
Це справедливо незалежно від того, наскільки ризикованими є ті ж цінні папери, узяті окремо, тобто недостатньо інвестувати просто в якомога більшу кількість цінних паперів, потрібно уміти правильно вибирати необхідні цінні папери.
Тобто, найважливіший принцип диверсифікації – розподіл капіталу між фінансовими інструментами, ціни на які по-різному реагують на одні і ті ж економічні події (або мають коефіцієнт кореляції менше 1).
Приклад. Проілюструємо обчислення прибутковості портфеля на прикладі портфеля з трьох акцій.
Інвестор на початку року придбав 100 акцій компанії A, 200 акцій компанії B і 100 акцій компанії C за ціною 40 у.о., 35 у.о. і 62 у.о. за акцію A, B, C, відповідно. Інвестор очікує, що в кінці періоду вартість однієї акції компанії A складе 46.48 у.о., однієї акції компанії В – 43.61 у.о, а компанії С – 76.14 у.о.
Тоді, користуючись наведеними вище формулами, знайдемо:
– початкову вартість портфеля: Vb=100×40+200×35+100×62= 17200 у.о;
- очікувану вартість портфеля в кінці періоду: Ve=100×46,48+200×43,61+100×76,14=20984 у.о.
Таким чином, прибутковість даного портфелю складе: r = (Ve/Vb) -1 = =0,22 або 22%.
8.2 Коефіцієнт бета
Познайомимось з ще одним важливим фінансовим показником, який використовується для оцінювання портфельного інвестування.
Бета – спеціальний фінансовий показник, який використовується для вимірювання величини систематичного ризику. Він характеризує нестійкість (мінливість) доходу даного виду цінних паперів щодо вартості ринкового портфеля. Формула розрахунку коефіцієнтного бета для активу у складі портфеля цінних паперів така :
де ra – прибутковість активу; rp – прибутковість портфеля цінних паперів.
Систематичний ризик враховується в моделі САРМ за допомогою коефіцієнтного бета. Коефіцієнтний бета відображає амплітуду коливань цін на акції конкретної компанії порівняно зі зміною цін на акції по всіх компаніях на даному сегменті ринку [20].
Більш висока чутливість до систематичного ризику припускає більш високу ринкову премію і навпаки. Компанія, коефіцієнтний бета якої більше одиниці, є більш ризикованою, ніж "середня" компанія, у той час як значення бета нижче одиниці вказує на менший ризик, ніж на ринку в цілому.
Коефіцієнтний бета може набувати додатних значень, що лежать від 0 і вище. Наприклад, значення коефіцієнтного бета більше 0 говорить про додатну кореляцію між даною акцією й ринковим індексом, тобто зростання індексу, так само як і його падіння, супроводжується зростанням/падінням акції, однак з різною швидкістю, про яку і говорить показник коефіцієнтного бета. Наприклад, значення коефіцієнтного бета 1,5 говорить про те, що мінливість прибутковості даної акції вище в 1,5 раза, ніж в індексу. Якщо індекс виріс на 1%, то наша акція на 1,5%, те ж саме справедливе і для падіння.
Значення коефіцієнтного бета 0 сигналізує про те, що мінливість прибутковості акції практично ніяк не залежить від мінливості фондового індексу. Досить часто акції, що мають коефіцієнтний бета вище 0, але менше 1, називають оборонними (defensive stocks).
Коефіцієнтний бета показує, як ринок впливає на зміну прибутковості портфеля. Він виражає кількісне співвідношення між рухом курсу даної акції і рухом ринку акцій в цілому Значення коефіцієнтного бета більше 1 говорить про більший ризик активів відносно ринку, менше 1 – про менший ризик.
При 
= 0,33 дохідність цінних паперів буде зменшуватися або збільшуватися втричі менше, ніж у всього ринку, і такий цінний папір буде мати тільки третину ризику ринкового портфеля, а зміни середньої дохідності в цьому випадку менше в 3 рази, ніж зміни середньої дохідності.
При 
= 1,5 рух, а отже, і ступінь ризику акції в півтора раза вище, ніж у ринку. Ціна портфеля, що складається з акцій 
=1,5, зростає або спадає швидше, ніж ціна усього ринку.
Теоретично коефіцієнтний бета 
може бути від’ємним. Це говорить про обернену залежність між курсом цінного паперу і індексом. Це має місце у випадку, коли дохідність ринкового портфеля зростає, а окремої акції – спадає, і навпаки. Наприклад, коефіцієнтний бета, який дорівнює -0,5, говорить про те, що при падінні індексу на 10% ціна акції виросте на 5%. На дійсній практиці цей випадок дуже рідкісний.
Цінні папери з 
>1 вважають високоризикованими (якщо падає середня дохідність ринку, то дохідність цих паперів спадає ще швидше). Чим більший коефіцієнтний бета 
, тим вищий системний ризик даного цінного паперу. Цінний папір з 
> 1 називають агресивним інвестиційним інструментом, а з 
< 1 – захисним інвестиційним інструментом [20].
Отже значення коефіцієнтного бета вираховується на основі даних минулих періодів. Для знаходження 
можуть бути також використані такі формули:
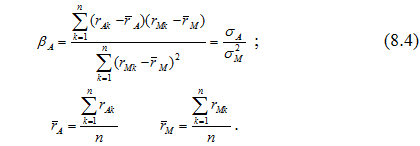
Може бути використана і інша формула, застосування якої в деяких випадках спрощує розрахунки:
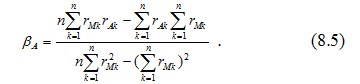
Отже, величина показує зміни прибутку конкретного цінного паперу компанії А на одиницю зміни середньоринкового доходу, коефіцієнтний бета інколи називається індексом ринкової чутливості даного цінного паперу.
Одна з властивостей коефіцієнтного бета портфеля полягає в тому, що він являє собою зважене середнє коефіцієнтів бета цінних паперів, що входять до нього, де як ваги виступають частини інвестицій в ці папери.
Для інвестиційного портфеля коефіцієнтний бета обчислюється шляхом додавання всіх бета паперів, що входять до його складу, помножених на відповідні ваги (вага кожного паперу в портфелі дорівнює частці від ділення її сукупної вартості в портфелі на вартість всього портфеля).
Для портфеля цінних паперів коефіцієнтний бета 
обраховується як середньозважена величина значення 
індивідуальних цінних паперів:
Даний вираз еквівалентний такому:
Тут 
p – коефіцієнтний бета портфеля, який відображає рух даного портфеля відносно всього ринку; 
A – коефіцієнтний бета цінного паперу А; wA – частка інвестицій в портфелі, що припадає на цінний папір.
Існує ще один фундаментальний показник ризикованості фінансового активу чи портфеля відносно ринку – це коефіцієнтний альфа (α).
Альфа-коєфіцієнт (α) – це коефіцієнт, що показує частку доходу, обумовлену внутрішніми чинниками, тобто пов'язану з несистематичним ризиком. Несистематичний ризик – ризик індивідуальних активів, не пов'язаний з фоновими соціально-економічними процесами. Він підлягає контролю з боку інвестора і може бути значно знижений. Коефіцієнтні альфа (α) і бета (β) є кількісними характеристиками залежності зміни ціни окремого цінного паперу від зміни значення ринкового індексу.
Якщо коефіцієнтний бета (β) показує чутливість ціни окремого цінного паперу до значення індексу, то коефіцієнтний альфа (α) показує незалежний від змін індексу рівень зростання (спадання) ціни цінного паперу.
Формула розрахунку коефіцієнтний альфа подана таким чином:
Приклад 1. Якщо в портфель входять 4 акції, три з яких мають 
= 0,8, а одна з акцій має 
= 2, то 
– коефіцієнт такого портфеля дорівнює:
Якщо одну з акцій (наприклад, акцію з 
=2) замінити на акцію з 
= 0,2, то коефіцієнтний бета 
портфеля знизиться і буде дорівнювати:
p = 0,8×0,25+0,8×0,25+0,8×0,25+0,2×0,25=0,65.
Приклад 2. Припустимо, інвестору необхідно вибрати один з двох інвестиційних портфелів – портфель I, портфель II, які сформовані з цінних паперів трьох видів (A, B, C). Інвестиційні величини коефіцієнтного бета та частки цінних паперів в портфелі показані в табл. 8.1.
Розрахуємо величини коефіцієнтних 
для обох портфелів:
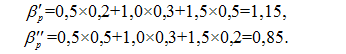
Незважаючи на те, що цінні папери, які містяться в обох портфелях, однакові, портфель І більш ризикований, ніж портфель ІІ, оскільки в ньому вища частка цінного паперу С, що характеризується менш високим ризиком і менша частка цінного паперу А, що характеризується менш високим ризиком.
Таблиця 8.1 – Дані для обрахунку коефіцієнтного бета 
портфеля
|
|
Частка цінного паперу в портфелі І |
Частка цінного паперу в портфелі ІІ |
wA |
0,5 |
0,2 |
0,5 |
wB |
1,0 |
0,3 |
0,3 |
wC |
1,5 |
0,5 |
0,2 |
- коефіцієнт цінного паперуТаким чином, ризик портфеля може бути знижений за рахунок включення в портфель цінних паперів, котрі мають більш низьке значення 
– коефіцієнта, ніж ті, які вже входять до складу портфеля.
Диверсифікація портфеля знижує рівень ризику: дійсно, якщо до складу портфеля входять акції однієї компанії-емітента на загальну суму 2 млн. грн, то заміна їх на акції двох різних компаній по 1 млн. грн, але з тими ж значеннями коефіцієнтних бета 
, дозволяє зберегти дохідність портфеля, але при цьому знижується ризик портфеля, що характеризується величиною 
р .
Приклад 3. Нехай портфель складається з таких цінних паперів: акції компанії Able, Baker та Charlie входили до складу ринкового портфеля в співвідношенні 0,12 : 0,19 : 0,69. Було підраховано, що очікуваний дохід ринкового портфеля 
дорівнює 22,4%, а середньоквадратичне відхилення 
= 15,2%.
Нижче подано вектор очікуваної дохідності та коваріаційна матриця:
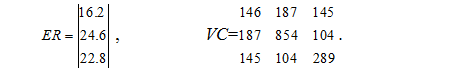
Нижче наведено обчислення коваріації акцій компаній Able, Baker та Charlie з ринковим портфелем:
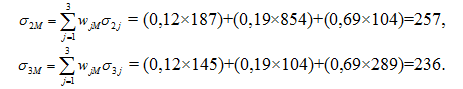
Формула (8.4) може бути використана для обчислення коефіцієнтів коефіцієнтних бета для акцій кожної компанії. Коефіцієнтні бета для акцій компаній Able, Baker та Charlie дорівнюють відповідно:
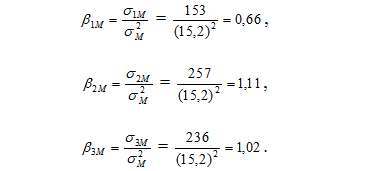
Коефіцієнтні ”альфа” для акцій компаній Able, Baker та Charlie обраховуються за формулою (8.7) та дорівнють відповідно:
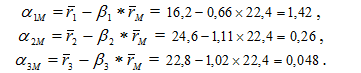
8.3 Служби з оцінювання «бета»- коефіцієнтів
У ряді країн існують спеціальні служби, що готують дані щодо коефіцієнтного бета і регулярно їх публікують. Багато хто з них користуються тільки даними про минулі коливання цін для формування прогнозів. Деякі одержують свої оцінки шляхом використання більш загальних факторних моделей. Одні служби користуються щотижневими даними за дворічний період, інші – щомісячними даними за п’ятирічний період. Одні оцінюють коефіцієнтні бета для американських цінних паперів на основі індексу Standard & Poo’s500 , інші – на основі сукупного індексу Нью-Йоркської фондової біржі та інших. У кожному випадку оцінки, зроблені для індивідуальних паперів, часто бувають помилковими. Тобто зовсім не дивно, що оцінки коефіцієнтного бета одного і того ж паперу, отримані на основі різних методик і різними службами, не збігаються. Це не означає, що різні оцінки коефіцієнтних бета марні. Однак відноситися до них потрібно з обережністю.
Недоліки розрахунку коефіцієнта бета.
У класичному варіанті розрахунку коефіцієнтного бета як показника відносної сили акції до ринку, є ряд недоліків.
1. Такий коефіцієнтний бета β не дає точного уявлення про силу акції до ринку. Якщо коефіцієнтний бета, припустимо, дорівнює двом, то це значить, що акція зростає в два рази швидше ринку і спадає в два рази швидше. А це не входить у визначення сильної (слабкої) акції.
Сильною до ринку вважається та акція, що на зростаючому ринку зростає більше, а на спадному ринку спадає менше (або зростає), ніж фондові індекси.
Слабкою до ринку вважається та акція, що на зростаючому ринку зростає менше (або спадає), а на спадному ринку спадає більше, ніж фондові індекси.
2. Такий коефіцієнтний бета β не враховує неефективність ринку в часі. Для його розрахунку використовується процес припасування періоду акції до періоду індексу. Іншими словами в розрахунку не враховується можливість тимчасового розриву в русі активів, що порівнюються. Так, індекс може вирости протягом 10 днів, а акція, що порівнюється, виросла на більшу величину за останні два дні. За цей період буде видно, що акція сильніше ринку (у цьому періоді), а класичний показник бета скаже, що бета менше 1. Це з тієї причини, що вісім днів з десяти акція не зростала, а ринок показував зростання [19].
Питання для самоперевірки
- Що таке диверсифікація портфеля? Для чого вона потрібна?
- Сформулюйте найважливіший принцип диверсифікації.
- Дайте означення та стислу характеристику коефіцієнтного бета.
- Що показує коефіцієнтний бета?
- Що таке високоризиковані папери?
- Як розраховується коефіцієнт бета для цінного паперу?
- Як розраховується коефіцієнт бета портфеля?
- Які Ви знаєте служби з оцінювання коефіцієнтного бета?
- Які знаєте недоліки розрахунку коефіцієнтного бета?
