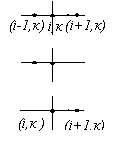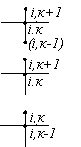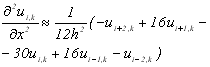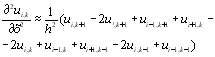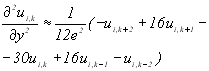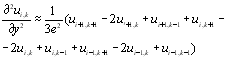Розглянемо рівняння 2-го порядку з двома невідомими незалежними змінними:
![]() , (11.1)
, (11.1)
де х, у – незалежні змінні; u – шукана функція; uх, uу, uхх, uуу – її 1-і та 2-і частинні похідні за аргументами х та у.
Розв'язком рівняння (11.1) називається функція ![]() , яка перетворює це рівняння в тотожність. Графік функції розв‘язку представляє поверхню у просторі ОХУ (інтегральна поверхня) (рис. 11.1).
, яка перетворює це рівняння в тотожність. Графік функції розв‘язку представляє поверхню у просторі ОХУ (інтегральна поверхня) (рис. 11.1).
Рівняння (11.1) називається лінійним, якщо воно відносно 1-го степеня шуканої функції i всіх її похідних, i не стримує їхні добутки, та може мати вигляд:
![]() , (11.2)
, (11.2)
де коефіцієнти А, В, С, Е можуть залежати від х, у і в окремих випадках можуть бути константами. Для класифікації ДР в частинних похідних вводиться термін дискримінант рівняння: Д = АС – В2 . Залежно від знака дискримінанта Д, лінійне диференційне рівняння (11.2) можна віднести до одного з таких типів:
якщо Д > 0, то рівняння (11.2) відноситься до еліптичного;
якщо Д = 0, то рівняння (11.2) відноситься до параболічного;
якщо Д < 0, то рівняння (11.2) відноситься догіперболічного.
У наступних розділах розглянемо приклади кожного з трьох типів рівнянь з відповідними граничними умовами і розглянемо для них чисельні методи розв’язання. Слідує відмітити, що еліптичні рівняння описують установлені процеси (стаціонарні), а гіперболічні та параболічні рівняння описують еволюційні процеси.
11.1 Різницеві методи розв'язування диференційних рівнянь у частинних похідних
Класичне визначення похідної функції однієї змінної записується у вигляді
![]() .
.
Природно, в ЕОМ не можна зробити граничного переходу. З іншого боку, можна додати деяке мале, хоча і ненульове, значення h і спробувати перевірити, що наближення виходить досить точним (проблема точності) і що помилка не зростає в ході процесу обчислень (проблема стійкості), тобто цей метод зводиться до того, що похідну заміняємо різницею.
Оскільки тепер є дві незалежні змінні, то обидві вони повинні брати участь у різницевому рівнянні. Розглянемо спочатку різниці в напрямку х.
Розклад функції ![]() в ряд Тейлора в околі точки (
в ряд Тейлора в околі точки (![]() ,
, ![]() ) можна записати у вигляді:
) можна записати у вигляді:
![]()
де ![]() лежить між х і х0. Якщо тепер представити
лежить між х і х0. Якщо тепер представити ![]() , то після деяких перетворень одержуємо
, то після деяких перетворень одержуємо
![]()
Класичне визначення похідної функції однієї змінної можна записати:
![]() .
.
Очевидно, на ЕОМ неможливо провести граничний перехід. А тому із розкладу функції в ряд Тейлора в околі точки ![]() можна наближено записати
можна наближено записати
![]() (11.3)
(11.3)
з помилкою обмежування ![]() ;
; ![]() .
.
Вираз (11.3) називають правою різницею, а вираз
![]() (11.4)
(11.4)
лівою різницею.
Користуючись (11.3) та (11.4), можна отримати різницевий вираз для 2-ї похідної
![]() (11.5)
(11.5)
і відповідно
![]() , (11.6)
, (11.6)
де h, k – величина кроку відповідно за координатами х та у.
Помилка обмеження дорівнює
![]()
![]() .
.
Аналогічно (11.5) і (11.6), можна вивести вираз для ![]() . Використовуючи ці вирази, загальновідоме рівняння Лапласа
. Використовуючи ці вирази, загальновідоме рівняння Лапласа ![]() , наприклад, можна записати в кінцевих різницях у вигляді:
, наприклад, можна записати в кінцевих різницях у вигляді:
![]() (11.7)
(11.7)
11.2 Етапи чисельного розв'язування диференційних рівнянь (ДР) у частинних похідних на ЕОМ
1. У область розв'язування рівняння, яке розглядається, вводять рівномірну сітку ![]() вузлових точок відповідно до характеру задачі і граничних умов.
вузлових точок відповідно до характеру задачі і граничних умов.
2. Диференційне рівняння, що розв'язується, записують у найзручнішій системі координат, замінюючи похідні кінцевими різницями (із таб. 11.1), приводять його до вигляду різницевого рівняння. Отримане різницеве рівняння використовують далі для описування функціонального зв'язку між сусідніми вузлами сітки. Тобто різницеве рівняння записують для усіх вузлів сітки і отримують внаслідок цього систему (N-1)(M-1) рівнянь з (N-1)(M-1) невідомими.
3. Систему (N-1)(M-1) рівнянь з (N-1)(M-1) невідомими розв'язують одним із відомих швидких і ефективних чисельних методів, вибір яких визначається деякими властивостями системи рівнянь (наприклад, система лінійних або налінійних рівнянь та ін.).
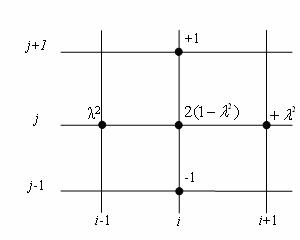
Помітимо, що рівняння (11.7) можна представити схематично, накресливши п'ять вузлів різницевого рівняння (11.7) і позначивши біля кожного з них відповідний коефіцієнт. Рисунок (наприклад, рис. 11.2) називається різницевою схемою.
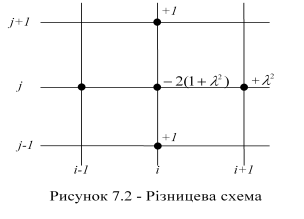
Різницева схема геометрично ілюструє різницеву апроксимацію диференціального рівняння. Відомо, що при ![]() і
і ![]() різницеве рівняння наближується до диференційного рівняння. Однак цікавить зовсім інше питання: чи наближається при
різницеве рівняння наближується до диференційного рівняння. Однак цікавить зовсім інше питання: чи наближається при ![]() і
і ![]() розв’язок різницевого рівняння до розв’язку диференційного рівняння? Для еліптичних рівнянь на це питання можна дати позитивну відповідь. Далі побачимо що у випадку параболічних і гіперболічних рівнянь прийдеться дотримуватись ряду обмежень, що забезпечать такого роду збіжність.
розв’язок різницевого рівняння до розв’язку диференційного рівняння? Для еліптичних рівнянь на це питання можна дати позитивну відповідь. Далі побачимо що у випадку параболічних і гіперболічних рівнянь прийдеться дотримуватись ряду обмежень, що забезпечать такого роду збіжність.
11.3 Еліптичні рівняння
До еліптичних відносять рівняння виду:
рівняння Пуассона ![]() (11.8)
(11.8)
рівняння Лапласа ![]() (11.9)
(11.9)
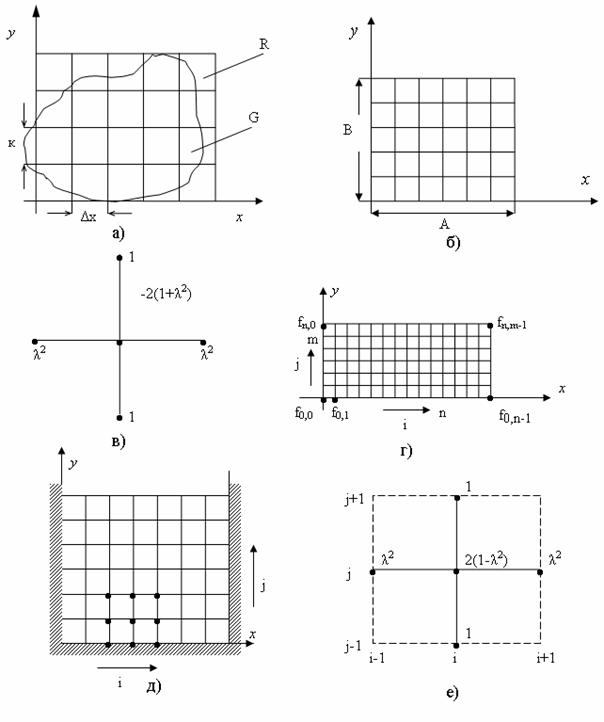
Розглянемо класичну задачу Діріхле
![]()
у деякій області R і ![]() на границі цієї області, якою є крива G. Звичайно, рівняння (11.9) являє собою рівняння Лапласа, окремий випадок рівняння Пуассона.
на границі цієї області, якою є крива G. Звичайно, рівняння (11.9) являє собою рівняння Лапласа, окремий випадок рівняння Пуассона.
Припустимо що область R має вигляд прямокутника ширини А і висоти В (рис. 11.3, 11.4.б).
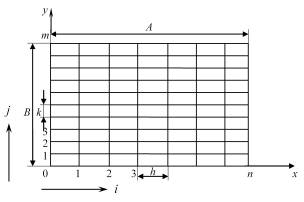
Розділимо спочатку ширину прямокутника А на n інтервалів, кожен розміром ![]() ; а висоту В – на m частин розмірами
; а висоту В – на m частин розмірами ![]() . Усередині області виходять при цьому
. Усередині області виходять при цьому ![]() перерізів сітки. Визначимо різницеве співвідношення для кожної внутрішньої точки і розв‘яжемо отриману систему рівнянь.
перерізів сітки. Визначимо різницеве співвідношення для кожної внутрішньої точки і розв‘яжемо отриману систему рівнянь.
Таблиця 7.1 – Відношення між похідними та значеннями функції у вузлах сітки
Похідна |
Схема |
Наближена формула |
Порядок похибки |
|
|
|
h2 h h |
|
|
|
e2 e e |
|
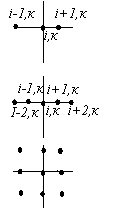
|
|
h2 h4 h4 |
|
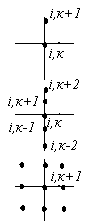 |
|
e2 e4 e4 |
Нумерація точок перетинання сітки починається в горизонтальному напрямку зліво-направо, від нуля, крайня права точка буде при цьому n-й. Аналогічно у вертикальному напрямку нумеруємо точки знизу-вверх від нуля до m. Вузол з індексами (i, j) буде i-м ліворуч і j-м знизу.
Нехай початок координат збігається з точкою, координати якої (0,0) позначимо
![]() ,
,
аналогічно записується
![]() .
.
Використовуючи таку систему позначень граничну умову (11.10) можна записати у вигляді:
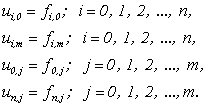 (11.11)
(11.11)
Якщо позначити ![]() , то диференціальне рівняння (11.9) зведеться до різницевого рівняння вигляду
, то диференціальне рівняння (11.9) зведеться до різницевого рівняння вигляду
![]() (11.12)
(11.12)
для i=1, 2, 3, …, n-1 та j=1, 2, 3, …, m-1...
При ![]() , тобто при однакових величинах інтервалів розбивки в горизонтальному і вертикальному напрямках, це співвідношення означає, що значення
, тобто при однакових величинах інтервалів розбивки в горизонтальному і вертикальному напрямках, це співвідношення означає, що значення ![]() є середнім арифметичним з чотирьох сусідніх з ним:
є середнім арифметичним з чотирьох сусідніх з ним:
![]() (11.13)
(11.13)
Важливо те, що одержана система – це система лінійних алгебраїчних рівнянь. Усього є ![]() рівнянь щодо
рівнянь щодо ![]() невідомих. Після того як
невідомих. Після того як ![]() 2(m+n) невідомих будуть виключені за допомогою граничної умови (11.11), залишається точно
2(m+n) невідомих будуть виключені за допомогою граничної умови (11.11), залишається точно ![]() рівнянь щодо
рівнянь щодо ![]() невідомих. Вираз (11.7) являє собою систему лінійних алгебраїчних (n-1)(m-1) рівнянь відносно (n+1)(m+1) невідомих. Після того, як 2(n+m) невідомі будуть виключені за допомогою граничних умов, залишається (n-1)(m-1) рівняння відносно (n-1)(m-1) невідомих.
невідомих. Вираз (11.7) являє собою систему лінійних алгебраїчних (n-1)(m-1) рівнянь відносно (n+1)(m+1) невідомих. Після того, як 2(n+m) невідомі будуть виключені за допомогою граничних умов, залишається (n-1)(m-1) рівняння відносно (n-1)(m-1) невідомих.
У (11.11) і (11.12) кожна пара значень (і, j) визначає вузол, в якому рівняння (11.6) розв'язується відносно ![]() . Рівняння (11.12) можна легко запам'ятати, якщо знати різницеву схему п'яти вузлів (рис. 11.2, 11.4.д,е).
. Рівняння (11.12) можна легко запам'ятати, якщо знати різницеву схему п'яти вузлів (рис. 11.2, 11.4.д,е).
Розпишемо докладно деякі з рівнянь (11.12). Для зручності прийнявши ![]() , тобто
, тобто ![]() , але спільність висновків не важко перевірити при кожному
, але спільність висновків не важко перевірити при кожному ![]() . Починаючи з
. Починаючи з ![]() і при незмінному
і при незмінному ![]() пройдемо значення
пройдемо значення ![]() :
:
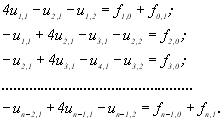 (11.14)
(11.14)
Тепер збільшуючи ![]() до 2, пройдемо значення при
до 2, пройдемо значення при ![]() :
:
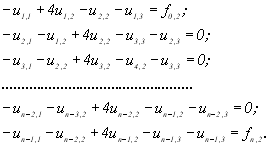 (11.15)
(11.15)
В такий же спосіб, збільшуючи щоразу ![]() і проходячи значення
і проходячи значення ![]() . Кінцеве значення
. Кінцеве значення ![]() буде дорівнювати
буде дорівнювати ![]() .
.
Система (11.14), (11.15) має дві важливі властивості, що допомагають вибрати для неї метод розв’язку. Властивості ці наступні:
1. Переважаюча частина коефіцієнтів системи дорівнює нулю.
2. У кожному рівнянні один з коефіцієнтів дорівнює + 4. Якщо в рівнянні є п'ять коефіцієнтів, відмінних від нуля, то сума інших чотирьох коефіцієнтів дорівнює – 4, якщо ж кількість ненульових коефіцієнтів менше п'яти, то сума інших дорівнює – 2 чи – 3.
Таким чином, у цій системі виконані умови збіжності ітераційного методу Гаусса - Зейделя (на основі її другої властивості). Перша ж властивість системи робить рішення методом виключення дуже незручним: вихідна система з великою кількістю рівних нулю коефіцієнтів перетвориться після виключення невідомих у повну трикутну систему.
Розглянемо деякі рівняння в тому вигляді, у якому з ними будуть проводитися ітерації. Позначаючи верхніми індексами порядковий номер ітерації і припускаючи, ![]() для усіх
для усіх ![]() , одержимо наступний порядок розв’язання системи рівнянь:
, одержимо наступний порядок розв’язання системи рівнянь:
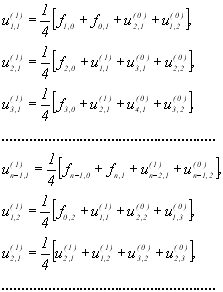 (11.16)
(11.16)
Для цієї системи рівнянь виконується умова зближення ітераційного методу Гауса - Зейделя. Щоб розв'язати цю систему, розроблено алгоритм (рис. 11.5), який використовує метод Гауса–Зейделя, який застосовують до еліптичних рівнянь різницевих, називають методом Лібмана (або методом послідовних зсувів).
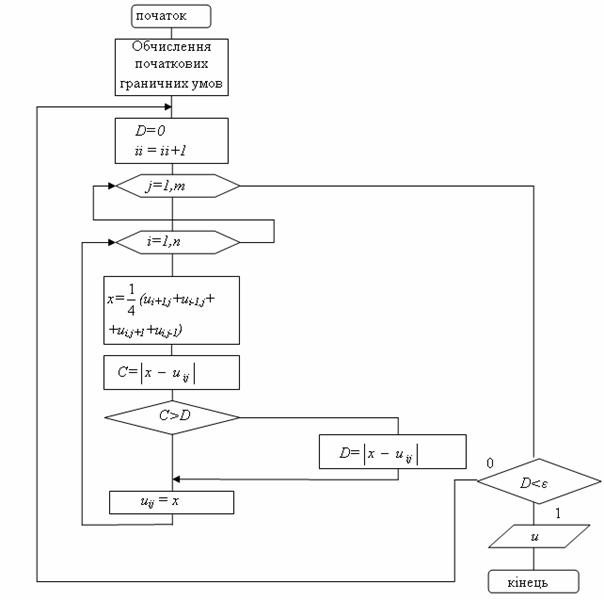
При порівнянні реальних систем ДР буває корисно збільшити чи зменшити чергове виправлення при розрахунку чергового наближення до кореня рівняння (аналогічний метод може виявитися корисним при розв’язанні систем лінійних алгебраїчних рівнянь). У дійсності це справедливо і для методу Лібмана. Щоб можна було збільшувати чи зменшувати чергові виправлення, замінимо в алгоритмі (рис. 11.5) визначення ![]() за формулою:
за формулою:
![]()
де х – значення ui,j, обчислене з рівняння (11.12). Параметр ? називається прискорюючим множником. У загальному випадку вимагається, щоб значення ? лежало в межах від 1 до 2. Якщо ? = 1, то є звичайний метод Лібмана, при ? > 1 є прискорений метод Лібмана..
Метод Лібмана було розглянуто тільки для випадку рівняння Лапласа. Взагалі кажучи, будь-яке еліптичне рівняння без членів, що містять иху, зводиться до системи різницевих рівнянь, що задовільняє умовам збіжності.
Усе сказане дотепер відносилося до лінійних рівнянь. Питання про збіжність для нелінійних рівнянь розроблено дуже слабо. Потрібно відзначити, однак, що багаторазово робилися успішні спроби вирішення квазілінійних (квазілінійними називаються рівняння, лінійні по ихх, uyy і uxy, але нелінійні по ux, иу, і, х, у) рівнянь за допомогою екстрапольованого методу Лібмана. Загальний підхід у цьому випадку зводиться до того, що задається навмання деяке значення і спостерігається швидкість збіжності інтераційного процесу. Потім, змінюючи ? і спостерігаючи викликані цим зміни швидкості збіжності, можна підібрати таке її значення, при якому ітераційний процес сходиться швидше всього. Вдавалося одержати збіжність навіть для рівнянь із членом типу иху, хоча в цьому випадку немає ніяких теоретичних основ очікування збіжності.
Є багато інших способів вирішення різницевих рівнянь (11.12). Найбільш часто використовуються лінійна релаксація, блокова релаксація і метод напрямків, що чергуються. Часто вони виявляються більш ефективними, ніж метод Лібмана. Нарешті, можна використовувати екстраполяційний перехід до границі.
11.4 Гіперболічні рівняння
Знайомство з даним типом диференційних рівнянь у частинних похідних почнемо з розгляду відповідної фізичної задачі.
Припустимо, що струна довжиною L, натягнута між двома точками осі х, точкою х = 0 і точкою x = L. Натяг струни дорівнює Т. Якщо відхилити струну від положення рівноваги і відпустити, то вона почне коливатися. Зсув кожної точки струни щодо положення рівноваги залежить не тільки від координати х цієї точки, але і від часу t. Відхилення струни від положення рівноваги описується рівнянням гіперболічного типу, що наводиться без виведення
![]()
для ![]() і t>0. Коефіцієнт а враховує фізичні характеристики Тут ? – вага струни на одиницю довжини, Т – натяг, g – прискорення сили ваги. Це рівняння звичайне називається хвильовим рівнянням. Для простоти а = 1, так що задача виразиться в такий вид:
і t>0. Коефіцієнт а враховує фізичні характеристики Тут ? – вага струни на одиницю довжини, Т – натяг, g – прискорення сили ваги. Це рівняння звичайне називається хвильовим рівнянням. Для простоти а = 1, так що задача виразиться в такий вид:
![]() (11.17)
(11.17)
![]() (11.18)
(11.18)
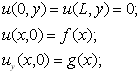
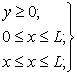 (11.19)
(11.19)
![]()
Таке формулювання задачі зовсім не означає втрати спільності, тому що проста заміна змінних зводить будь-яке хвильове рівняння до виду (11.17).
Оскільки кінці струни закріплені, то
![]()
![]() , (11.20)
, (11.20)
початковими умовами є початковий зсув
![]() ,
, ![]() (11.21)
(11.21)
та початкова швидкість
![]()
![]() (11.22)
(11.22)
Наприклад, якщо відтягнути струну за середину, як показано на рис. 11.6 і відпустимо її без додавання їй початкової швидкості, то початкові умови запишуться у вигляді
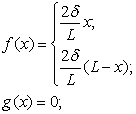
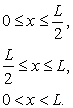
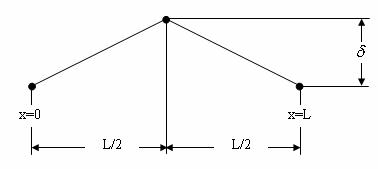
Помітимо, що ці умови називаються початковими, а не граничними. У дійсності, якщо задати для гіперболічного рівняння граничні умови, то отримана задача не буде мати єдиного розв’язку. Подібні задачі називаються некоректно поставленими. Дуже важливо, щоб додаткові умови належним чином відповідали кожному типу рівнянь.
Щоб знайти різницеві рівняння, що відповідають (11.17), , скористаємося знову рівностями (11.18) і (11.19), причому замість у записується t. Знову накреслюючи сітку, але тепер ця сітка простирається нескінченно в напрямку позитивних значень t. Можна шукати роз’язок для як завгодно далекого моменту часу. У напрямку х приймаємо крок сітки рівним h, у напрямку t – рівним k. Тому інтервал L розділяється на п= L/h малих інтервалів h, а в напрямку t може бути як завгодно багато інтервалів k.
Якщо позначити
![]() і
і ![]() ,
,
то різницеве рівняння запишеться у вигляді
![]() (11.23)
(11.23)
для i = 1, 2, ..., п і для j = 1, 2, ... .
Різницева схема при цьому виглядає так(рис.11.7):
Граничну умову (11.20) легко записати у вигляді
![]() j = 1,2,3, ... (11.24)
j = 1,2,3, ... (11.24)
Початкову умову (11.21) можна написати у вигляді
![]() i=1,2,..,n-1... (11.25)
i=1,2,..,n-1... (11.25)
Щоб записати в різницевому вигляді початкову умову (11.22), можна використовувати рівність (11.3), тоді отримаємо:
![]() .
.
Після цього, використовуючи (11.25), одержуємо
![]() (11.26)
(11.26)
Помітимо тепер, що (11.25) і (11.26) дають значення ![]() для перших двох рядків: (j = 0 і j = 1). Підставляючи j = 1 у (11.23), одержимо
для перших двох рядків: (j = 0 і j = 1). Підставляючи j = 1 у (11.23), одержимо
![]() (11.27)
(11.27)
Усі доданки в правій частині цього рівняння включають значення і тільки з перших двох рядків сітки; всі ці значення відомі з початкових умов. Тому в останньому рівнянні є тільки одне невідоме і всі значення функції, що відповідають третьому рядку, можна обчислити в явному вигляді. Після цього можна обчислювати значення функції в четвертому рядку, виходячи зі значень у другому і в третьому рядках, і т.д. стільки разів, скільки буде потрібно. При цьому навіть не приходиться вирішувати систему рівнянь.
Таким чином, (11.27) являє собою явну схему рішення хвильового рівняння. Схема алгоритму представлена на рис. 11.8.
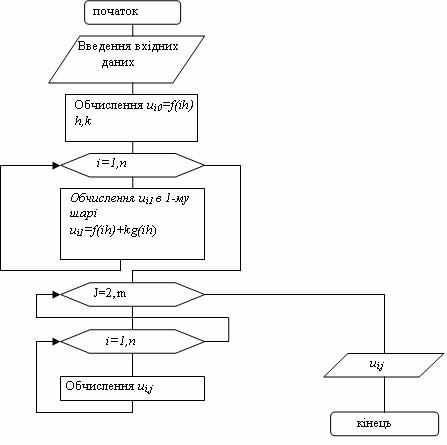
Рисунок 11.8 – Схема алгоритму розв'язування гіперболічного рівняння на ЕОМ
При роз’язанні еліптичного рівняння (11.13) було використано схему, в якої в кожному рівнянні було більш ніж по одному невідомому; таким чином, цей метод можна було назвати неявним.
Розглянемо тепер питання збіжності і стійкості методу (не приводячи доведень, а обмежуючись тільки аналізом остаточних результатів). Можна стверджувати, що рішення (11.27) сходиться (мається на увазі, що при h?0 і k?0 розв’язання різницевого рівняння асимптотично наближається до розв‘язання диференціального рівняння), якщо
![]() чи, що те ж саме, k
чи, що те ж саме, k
Ця умова є достатньою для збіжності; але вона не є необхідною. Іншими словами, існують рівняння і величини інтервалів, при яких ця умова не виконується, але усе-таки виходить вірний результат. Уся справа в тім, що тоді не можна гарантувати збіжність чисельного розв‘язку.
Таким чином, як тільки обрана величина інтервалу розбивки h у напрямку х, то з'являється обмеження на величину інтервалу по t. Якщо необхідно зробити обчислення для великого відрізка t, то може знадобитися велика кількість кроків.
Іншою настільки ж важливою обставиною є те, що при ![]() метод стає нестійким, як в абсолютному, так і у відносному змісті. Це означає, як і для звичайних диференційних рівнянь, що будь-які помилки зростають у ході обчислення розв’язку.
метод стає нестійким, як в абсолютному, так і у відносному змісті. Це означає, як і для звичайних диференційних рівнянь, що будь-які помилки зростають у ході обчислення розв’язку.
Література
1. Мак – Кракен Д., Дрон У. Численные методы и програмирование на фортране. – М.: Мир, 1977. – 584 с.
2. Бахвалов Н. С. Численные методы . Т. И. Анализ, алгебра, обычные диференциальные уравнения. – М.: Наука, 1975. – 631 с.
3. Ляшенко М.Я., Головань М.С. Чисельні методи: Підручник. Либідь. 1996. – 288 с.
4. Крылов В. И. и др. Численные методы . – М.: Наука, 1978. – 1979. – Т. 2. – 400 с.
5. Д. Мэтьюз, Г. Цинк, Д. Куртис. Численне методы. Использование Matlab, –М. Издательский дом “Вильямс”, 2001. – 720 с. 720 с.
6. Митчел Е., Уейк Р. Метод конечных елементов для уравнения с частными производными. – М.: Мир, 1981. – 216 с.
7. Трауб Дж. Итерационные методы решения уравнений. – М.: Мир, 1985. – 263 с.
8. Ортега Дж., Пуп У. Введение в численные методе решения диференциальных уравнений. – М.:Наука,1986. – 288 с.
9. Молчанов И. М. Машинные методы решения прикладных задач, диф. уравнений. – Киев: Наук. Думка, 1988. – 344 с.
10. Крилов В. И. и др. Начала теории вычислительных методов. Уравнения в часных производных. – Минск: Наука и техника, 1986. – 310 с.
11. Крилов В. И. и др. Начала теории вычислительных методов. Интегральное уравнение, некорректные задачи и улучшение сходимости. – Минск: Наука и техника, 1984. – 263 с.
12. Крилов В. И. Математический анализ. Ускорение сходимости. – Минск: Наука и техника, 1988. – 176 с.
13. Прикладные методы и программирование в численном анализе. – М.: Изд-во Моск. ун – ту, 1985. – 185 с.
Питання та задачі до самостійної роботи
1. Які рівняння відносять до рівнянь у частинних похідних?
2. Що таке дискримінант?
3. Класифікація рівнянь у частинних похідних.
4. Особливості трактування задачі розв'язання рівнянь в частинних похідних на ЕОМ.
5. Що таке дискримінант рівняння?
6. Що таке змішана задача?
7. Особливості різницевих методів. Навести наближені формули для похідних ![]()
![]() ,
, ![]() (за 2, 3, 5, 9 точками).
(за 2, 3, 5, 9 точками).
8. Різницева схема для розв'язування еліптичного рівняння на ЕОМ.
9. Алгоритми розв'язання еліптичного рівняння на ЕОМ.
10. Особливість методу Лібмана.
11. Особливість прискореного методу Лібмана
12. Різницева схема для розв'язування гіперболічного рівняння на ЕОМ
13. Різницева схема для розв'язування еліптичного рівняння на ЕОМ.
14. Різницева схема для розв'язування параболічного рівняння на ЕОМ
15. Особливість алгоритму розв'язання гіперболічного рівняння на ЕОМ.
16. Явні та неявні методи роз’язання гіперболічного рівняння на ЕОМ.
17. Явні та неявні методи роз’язання еліптичного рівняння на ЕОМ.