(10.1)
Як зазначалося вище, задача, що заключається в розв’язку звичайного диференційного рівняння при додаткових умовах, що поставлені при декількох значеннях незалежної змінної, називається крайовою.
Розглянемо звичайне диференційне рівняння другого порядку
(10.1)
при граничних умовах
(10.2)
Рівняння більш високих порядків можна вирішувати тими ж методами, які поділимо на дві групи:
1. Методи, основані на заміні розв’язку крайової задачі розв’язком декількох задач Коши.
2. Методи, в яких використовується кінцево-різницева форма диференціального рівняння.
Якщо звичайне диференційне рівняння другого порядку є лінійним, тобто має вигляд
(10.3)
при додаткових умовах
(10.4)
то крайову задачу можна звести до задачі Коши за допомогою початкових умов
і 
Знайшовши розв’язок 
можна поставити другі граничні умови
і 
і отримати другий розв’язок 
. Якщо 
а 
при чому 
то розв’язок
(10.5)
задовольняє обом початковим граничним умовам.
Якщо вирішується нелінійне звичайне диференційне рівняння, то розв’язок крайової задачі можна звести до розв’язку декількох задач Коши, послідовно вводячи в початкові умови значення 
:
(10.6)
і прагнучи найти розв’язок, який задовольняє умову 
При цьому може допомогти інтерполяція, що дозволяє побудувати впорядковану послідовність 
і звести до мінімуму об’єм обчислень.
Перевага кінцево-різницевих методів в тому, що вони дозволяють звести розв’язок крайової задачі до розв’язку системи алгебраїчних рівнянь. При розв’язку двоточкової крайової задачі
, (10.7)
при 
і 
інтервал 
можна розділити на n рівних частин:
, (10.8)
де 
а 
В точках 
, що називаються вузлами, намагаються найти значення розв’язок 
. Знаючи координати вузлів користуючись кінцево-різницевими виразами для похідних
(10.9)
(10.10)
можна представити диференціальне рівняння у виді різницевого рівняння.
а) якщо початкове ЗДР лінійне, то задача буде складатися з розв’язання системи лінійних алгебраїчних рівнянь;
б) якщо початкове ЗДР нелінійне, то задача зводиться до розв’язування системи нелінійних алгебраїчних або трансцендентних рівнянь;
в) методи, алгоритми та програми розв’язування таких лінійних та нелінійних рівнянь відомі, але звести розв’язування крайової задачі методом кінцевих різниць до стандартної програми важко, оскільки формулювання кожної задачі залежить від вигляду рівняння, що розглядається.
Приклад 10.1. Нехай потрібно вирішити диференціальне рівняння 
при умовах
і 
і кроці h=0.2. В різницевій формі це рівняння має вид
Використовуючи цю формулу і граничні умови можна виписати наступну систему чотирьох лінійних рівнянь з чотирма невідомими:
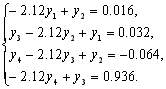
Якщо звичайне диференціальне рівняння (ЗДР) 2-го порядку розв’язати методом скінченних різниць, то початкове ЗДР зводиться до системи лінійних алгебраїчних рівнянь з тридіагональною матрицею коефіцієнтів, тобто такою, що кожне рівняння системи має три сусідні невідомі:
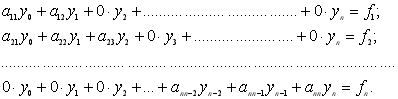(10.11)
Для розв’язання такої системи розроблено спеціальний метод – прогонки. Розглянемо лінійне диференціальне рівняння другого порядку
(10.12)
з двоточковими граничними умовами:
(10.13)
; 
, (10.14)
де функції 
, 
, 
неперервні на 
.
Прийдемо до скінченнорізницевого рівняння
; 
; 
; 
;
. (10.15)
Підставляючи вираз (10.15) у початкове ЗДР (10.12), отримаємо для внутрішніх точок 
систему скінченнорізницевих рівнянь:
. (10.16)
Після деяких перетворень (10.16) матимемо
; 
(10.17)
де
; 
; 
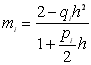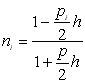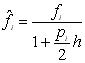. (10.18)
Для похідних на кінцях відрізка інтегрування 
і 
знаходимо скінченнорізницеві рівняння виду
; 
(10.19)
і, підставляючи їх у граничні умови (10.13) і (10.14), отримаємо два рівняння:
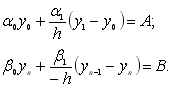(10.20)
Система 
рівнянь (10.17), (10.20) відносно невідомих 
являє собою систему лінійних алгебраїчних рівнянь з три діагональною матрицею коефіцієнтів. Цю систему зручно розв’язати методом прогонки.
Розглянемо суть цього методу.
1. Представимо рівняння (10.17) відносно 
:
. (10.21)
2. Допустимо, що за допомогою рівнянь (10.20) і (10.21) виключена складова 
, тоді рівняння будуть мати вигляд
(10.22)
де 
– деякі коефіцієнти.
3. За аналогією з (10.22) представимо 
у вигляді
(10.23)
і, підставляючи його в (10.17), матимемо
(10.24)
і, отже,
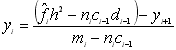. (10.25)
4. Порівнюючи вирази (10.22) та (10.25), отримуємо рекурентні формули для визначення коефіцієнтів 
, 
вигляду
; 
, 
. (10.26)
5. Для визначення виразу для 
та 
використовуємо рівняння (10.20) та (10.22):
; (10.27)
та 
. (10.28)
Порівнюючи останні дві нерівності, знаходимо:
; 
. (10.29)
На основі формул (10.17) та (10.29) послідовно визначаємо коефіцієнти 
до 
і 
включно. Процес знаходження коефіцієнтів називають прямим ходом методу прогонки.
Зворотній хід методу прогонки починається з визначення 
. Використовуючи другу граничну умову (10.20) та формулу (10.22), отримуємо систему з двох рівнянь:
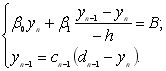(10.30)
Розв’язуючи цю систему відносно 
, отримаємо:
. (10.31)
Тепер за формулою (10.22) послідовно знаходимо розв’язок початкового ЗДР: 
Таким чином, метод прогонки достатньо простий, легко алгоритмізується та включає прямий та зворотній хід. Причому:
1) прямий хід полягає в знаходженні коефіцієнтів за рекурентними формулами (10.26);
2) зворотній хід полягає у знаходженні розв’язку початкового ЗДР за формулою (10.22).
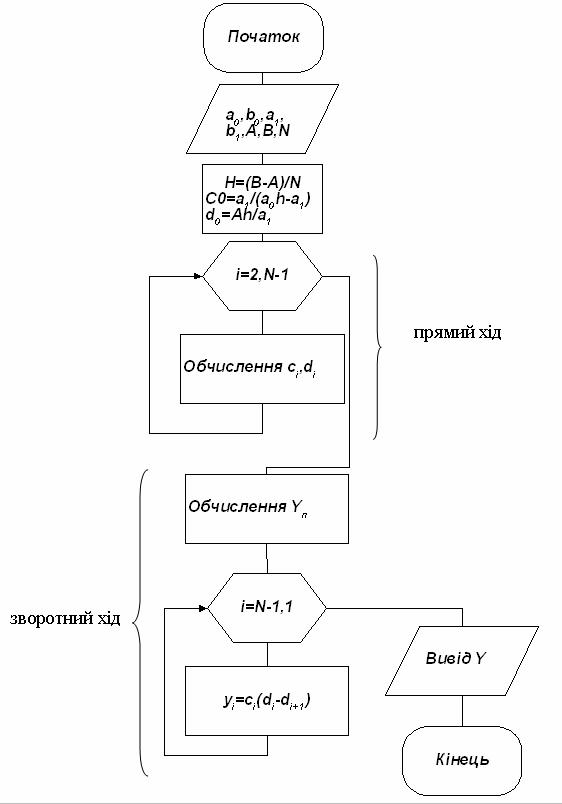
Схему алгоритму методу прогонки показано на рис. 10.1.
1. Фельдман Л.П., Петренко А.І. Дмитрієва О.А. Чисельні методи в інформатиці: Підручник/ За ред. М.З. Згуровського. – К.: Вид. група BHV, 2006. – 480 с.
2. Мак – Кракен Д., Дрон У. Численные методы и програмирование на фортране. – М.: Мир, 1977. – 584 с.
3. Бахвалов Н. С. Численные методы . Т. И. Анализ, алгебра, обычные диференциальные уравнения. – М.: Наука, 1975. – 631 с.
4. Ляшенко М.Я., Головань М.С. Чисельні методи: Підручник. Либідь. 1996. – 288 с.
5. Численные методы / Н. И. Данилина, Н. С. Дубровская, О. П. Кваша и др. – М.: Высшая шк., 1976. – 368 с.
6. Ракитский Ю. В., Устинов С. М., Черноруцкий И. Т. Численные методы решения жестких систем. – М.: Наука, 1979. – 587 c.
7. Плис А.И., Сливина Н.А. Mathcad. Математический практикум для инженеров и экономистов: – М.: Финансы и статистика, 2003. – 656с.
8. Д. Мэтьюз, Г. Цинк, Д. Куртис. Численне методы. Использование Matlab, –М. Издательский дом “Вильямс”, 2001. – 720 с. 720 с.
9. Иванов В. В. Методы вычислений на ЕОМ. – Киев: Наук. думка, 1986. – 584 с.
10. Маліков В.Т., Кветний Р.Н. Вычислительные методы и применение ЭВМ. – К.: Высшая школа., 1989. – 213 с.
11. Квєтний Р.Н. Методи комп’ютерних обчислень: Навчальний посібник. /МО І науки України. – Вінниця: ВДТУ, 2001. – 148 с.
12. Ортега Дж., Пуп У. Введение в численные методе решения диференциальных уравнений. – М.:Наука,1986. – 288 с.
13. Молчанов И. М. Машинные методы решения прикладных задач, диф. уравнений. – Киев: Наук. Думка, 1988. – 344 с.
14. Прикладные методы и программирование в численном анализе. – М.: Изд-во Моск. ун – ту, 1985. – 185 с.
1. Особливості розв’язування систем диференціальних рівнянь на ЕОМ.
2. Загальний підхід до розв’язання краєвої задачі.
3. В чому суть методу прогонки?
4. Дати визначення таким поняттям: краєва задача, межові умови, задача Коші, тридіагональна матриця. Навести приклад.
5. Суть алгоритму розв’язання крайової задачі скінченнорізницевими методами.
6. Особливості методу прогонки.
7. Суть прямого ходу методу прогонки.
8. Суть зворотного ходу методу прогонки.
9. Розв’язати ЗДР 
з межовими умовами: 
; 
та кроком 
.