Лекція № 9

     ЧИСЕЛЬНІ МЕТОДИ РОЗВ'ЯЗАННЯ ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ НА ЕОМ

 

Інженеру часто доводиться зіштовхуватись з диференційними рівняннями і системами диференційних рівнянь при розробці нових виробів чи технологічних процесів, так як більша частина законів фізики формалізується саме у вигляді диференційних рівнянь. Будь-яка задача проектування, яка зв’язана з розрахунком потоків енергії чи руху тіл, в кінцевому рахунку зводиться до розв’язку диференційних рівнянь. Нажаль, лише дуже малу частину з них можливо вирішити без допомоги обчислювальних машин. Тому чисельні методи розв’язку диференційних рівнянь відіграють важливу роль у практиці інженерних розрахунків.

     9.1. Основні визначення та поняття

Рівняння, у якому невідома функція входить під знаком похідної чи диференціала, називається диференціальним рівнянням. Наприклад,

,

Якщо невідома функція, що входить у диференціальне рівняння, залежить тільки від однієї незалежної змінної, то диференціальне рівняння називається звичайним. Наприклад, диференціальні рівняння

відносяться до звичайних.

Якщо ж невідома функція, що входить у диференціальне рівняння, є функцією двох чи більшого числа незалежних змінних, то таке рівняння називається диференціальним рівнянням у частинних похідних. Наприклад, диференціальне рівняння

відноситься до рівняння в частинних похідних.    

Порядком диференціального рівняння називається найвищий порядок похідної (чи диференціала), що входить у рівняння.

Розглянемо звичайні диференціальні рівняння.

Звичайне диференціальне рівняння n-го порядку в самому загальному випадку містить незалежну змінну, невідому функцію і її похідні чи диференціали до n-го порядку включно і має вид

               (9.1)

У цьому рівнянні х - незалежна змінна, у - невідома функція, - похідні цієї функції.

Розв'язком (чи інтегралом) рівняння (9.1) називається будь-яка диференціюєма функція, що задовольняє цьому рівнянню, тобто така, після підстановки, якої у рівняння (9.1) воно перетворюється в тотожність.

Графік розв’язку звичайного диференціального рівняння називається інтегральною кривою цього рівняння.

Розв’язок диференціального рівняння, що містить стільки незалежних довільних (постійних) параметрів, який його порядок, називається загальним розв'язком (чи загальним інтегралом) цього рівняння.

    
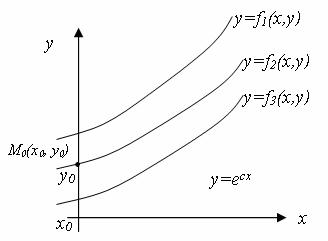
     Рисунок 9.1. – Сімейство інтегральних кривих диференціального рівняння (9.1)

Геометрично загальний розв’язок диференціального рівняння являє собою сімейство інтегральних кривих цього рівняння (рис. 9.1).

Частинним розв'язком диференціального рівняння називається будь-який розв’язок, що може бути отриманий з загального при визначених числових значеннях довільних постійних (рис. 9.1). Довільні постійні, що вхідять в загальний розв’язок, визначаються з початкових або крайових умов.

Задача з початковими умовами ставиться так: знайти розв’язок рівняння , що задовольняє додатковим умовам, які складаються в тім, що розв’язок , повинний приймати разом зі своїми похідними до (n-1)-го порядку задані числові значення при заданому числовому значенні незалежної змінної х.

Такі умови називаються початковими умовами, а задача відшукання розв‘язку диференціального рівняння (9.1), що задовольняє заданим початковим умовам - задачею з початковими умовами, або задачею Коші.

Задача з крайовими умовами ставиться так: знайти розв’язок рівняння , що задовольняє додатковим умовам, які складаються в тім, що розв’язок , повинний приймати разом зі своїми похідними до (n-1)-го порядку задані числові значення при заданому числовому значенні та при заданому числовому значені незалежної змінної х.

Такі умови називаються крайовими умовами, а задача відшукання розв‘язку диференціального рівняння (9.1), що задовольняє заданим крайовим умовам – крайовою задачею.

У випадку рівняння першого порядку, тобто при n=1, одержуємо задачу Коші для рівняння з початковою умовою

Геометрично задача Коші для рівняння першого порядку полягає в тому, що з усіх інтегральних кривих, що представляють собою загальний розв‘язок, потрібно знайти ту інтегральну криву, що проходить через точку М0 з координатами (рис.9.1).

Часто в задачі Коші у ролі незалежної змінної виступає час t. Прикладом може бути задача про вільні коливання тіла, яке підвішене на пружині. Рухи такого тіла описуються диференційним рівнянням, в якому незалежною змінною є час t. Якщо додаткові умови задані у вигляді значень переміщень чи швидкості при t=0, то це також задача Коші.

Задача Коші має єдиний розв‘язок, що задовольняє умові в якщо функція неперервна в деякій області і задовольняє в цій області умові Ліпшица,

де N - постійна Ліпшица, що залежить від а і b (а і b - границі області).    

Методи точного інтегрування диференціальних рівнянь придатні лише для порівняно невеликої частини рівнянь, що зустрічаються на практиці.

Тому в задачах моделювання та дослідження складних технічних систем, наприклад, систем автоматичного управління, великого значення набувають методи наближеного розв’язання диференційних рівнянь, що у залежності від форми представлення розв’язку можна розділити на дві групи:

1) аналітичні методи, що дають наближений розв’язок диференційного рівняння у виді аналітичного виразу;    

2) чисельні методи, що дають наближений розв’язок у вигляді таблиці.

Похибки. Перед тим, як перейти до розглядання методів чисельного розв'язання диференційних рівнянь, зупинимося на джерелах похибок, пов'язаних з чисельною апроксимацією. Таких джерел три:

1. Похибка округлення зумовлена обмеженнями на представлення чисел в ЕОМ, тому що число значущих цифр, що запам'ятовується і використовується в обчисленнях, обмежене.

2. Похибка відсічення зв'язана з тим, що для апроксимації функції замість

     при     (9.2)

нескінчених рядів часто використовується лише декілька перших їх членів.

    
     Рисунок 9.2 – Геометричне представлення накопичування похибки в процесі обчислень

Це звичайний для чисельних методів прийом, що являється джерелом похибки, цілком зумовлених використаним методом і не залежать від характеристик ЕОМ.

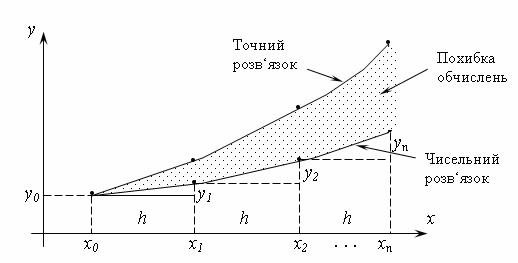
3. Похибка поширення являється результатом накопичення похибок, що з'явились у попередніх результатах розрахунку. Так як ні один з наближених методів не може дати зовсім точних результатів, то будь-яка виникла в процесі обчислень похибка зберігається і на наступних стадіях розрахунку (рис. 9.2).

Вказані три джерела похибок є причиною помилок двох типів:

Локальна помилка – сума похибок, що вносяться у розрахунковий процес на кожному етапі обчислення.

Глобальна помилка – різниця між розрахованим та точним значеннями величини на кожному етапі реалізації чисельного алгоритму, що визначає сумарну похибку, що накопичується з моменту початку розрахунку.

     9.2. Класифікація численних методів розв'язання задачі Коші

На протязі багатьох років чисельний розв‘язок задачі Коші був об‘єктом пильної уваги науковців оскільки він широко застосовується в різних галузях науки і техніки. Тому і кількість розроблених для нього методів дуже велика.

Чисельні методи розв'язання задачі Коші розділяються на 3 групи:

  •  одноточкові;

  •  багатоточкові (методи прогнозу та корекції);

  •  методи з автоматичним вибором кроку інтегрування.

    На рис. 9.3 представлена класифікація найбільш відомих чисельних методів розв‘язання диференційних рівнянь (ДР) на ЕОМ.

        
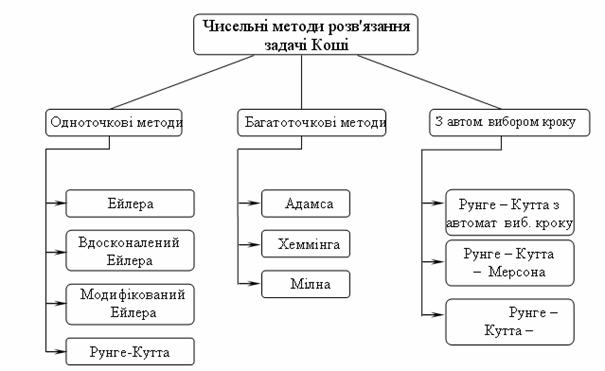
         Рисунок 9.3– Класифікація чисельних методів розв'язання задачі Коші.

    До одноточкових методів відносять методи, які мають певні загальні риси, такі як:

    1. В основі усіх одноточкових методів лежить розклад функції в ряд Тейлора, в якому зберігаються члени, що мають h в степені до k включно. Ціле число k називається порядком метода. Похибка на кроці має порядок k+1.

    2. Всі одноточкові методи не потребують дійсного обчислення похідних, тому що обчислюється лише сама функція, однак можуть потребуватися її значення в деяких проміжних точках. Це тягне за собою, звичайно, додаткові затрати часу і зусиль.

    3. Для отримання інформації у новій точці, потрібно мати дані лише в попередній точці. Цю властивість можна назвати „самостартуваням”. Властивість „самостартуваня” дозволяє легко змінювати величину кроку h.

    4. В порівнянні з одноточковими методами методи прогнозу і корекції мають ряд особливостей:

    1. Для реалізації методів прогнозу і корекції необхідно мати інформацію про декілька попередніх точок (вони не відносяться до „самостартуючих” методів), тому для отримання додаткової інформації доводиться застосовувати одноточковий метод. Якщо в процесі розв’язку диференційних рівнянь методом прогнозу і корекції змінюється крок, то звичайно тимчасово доводиться переходити до одноточкового методу.

    2. Одноточкові методи і методи прогнозу і корекції забезпечують приблизно однакову точність результатів. Однак другі на відміну від перших дозволяють лише оцінити похибку на кроці. З цієї причини, користуючись одноточковими методами, величину кроку h звичайно обирають трохи менше, ніж це необхідно, тому методи прогнозу і корекції виявляються найбільш ефективними.

    3. Використовуючи метод Рунге-Кутта четвертого порядку точності, на кожному кроці доводиться обчислювати чотири значення функції, але для збіжності методу прогнозу і корекції того ж порядку точності часто достатньо двох значень функції. Тому методи прогнозу і корекції вимагають майже вдвічі менше машинного часу, ніж методи Рунге-Кутта порівнюваної точності.

         9.3 Одноточкові методи розв'язання задачі Коші на ЕОМ

    Розв'язати диференційне рівняння чисельним методом - це значить для заданої послідовності аргументів і знайти такі значення що ) і Таким чином, чисельні методи дозволяють замість отримання функції одержати таблицю значень цієї функції для заданої послідовності аргументів. Величина називається кроком інтегрування.

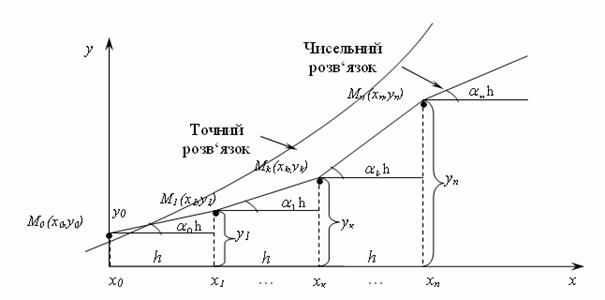
    Графічно чисельний розв‘язок уявляє собою послідовність коротких прямолінійних відрізків, якими апроксимується аналітичний розв’язок рівняння (кусочно-лінійна апроксимація).

    Розглянемо алгоритми найбільш відомих чисельних методів.

    Метод Ейлера є порівняно грубим і застосовується в основному для орієнтованих розрахунків. Однак ідеї, покладені в основу методу Ейлера, є базовими для інших методів.

    Нехай дано диференційне рівняння першого порядку

                   (9.3)

         з початковими умовами           (9.4)

    Потрібно знайти розв’язок рівняння на відрізку .

    Розіб'ємо відрізок на n рівних частин і одержимо послідовність де, а - крок інтегрування.

    Виберемо к-й відрізок і проінтегруємо рівняння (9.3):

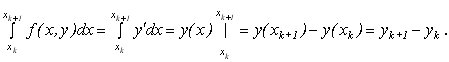    або

                   (9.5)

    Якщо в останньому інтегралі підінтегральну функцію на відрізку прийняти постійною і рівною початковому значенню в точці x = xk, то одержимо

    Тоді формула (6.5) прийме вигляд

                   (9.6)

    Позначивши , тобто , отримаємо

                   (6.7)

    Продовжуючи цей процес, і щораз приймають, що на відрізку інтегральна крива приблизно заміняється прямолінійним відрізком, що виходить із точки кутовим коефіцієнтом . Тому в якості наближення шуканої інтегральної кривої одержуємо ламану лінію з вершинами в точках (рис. 9.4).

        
         Рисунок 9.4 – Геометричне розв’язання методом Ейлера

    Якщо функція у деякій прямокутній області

    задовольняє умові

              (9.8)

    і, крім того,

                   (9.9)

    то має місце наступна оцінка похибки:

              ,     (9.10)

    де в y(хn) - значення точного розв’язку рівняння (9.3) при x = xn, а yn - наближене значення, отримане на n-м кроці.

    Формула (9.10) має в основному теоретичне застосування. На практиці, як правило, застосовують "подвійний прорахунок". Спочатку чисельне розв‘язання рівняння ведеться з кроком h, потім крок дроблять і повторний розрахунок ведеться з кроком h/2. Похибка більш точного значення оцінюється формулою

                   (9.11)

    Метод Ейлера може бути застосований до розв'язку систем диференційних рівнянь вищих порядків. Однак в останньому випадку диференційні рівняння повинні бути приведені до системи диференційних рівнянь першого порядку.

    Нехай задана система двох рівнянь першого порядку

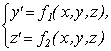                   (9.12)

    з початковими умовами

         .          (9.13)

    Наближені значення y(xi) y1 та z(xi)zi знаходяться по формулах

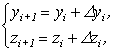                   (9.14)

        

                   (9.15)

    Схема алгоритму метода Ейлера представлена на рисунку 9.5.

        
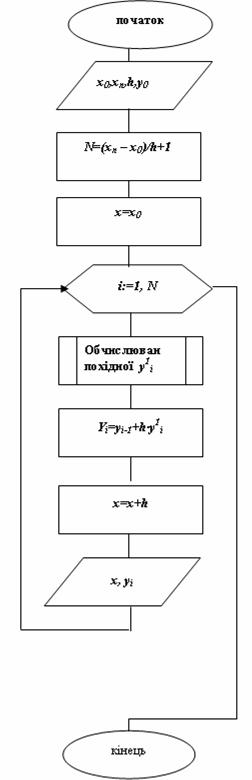
         Рисунок 9.5 – Схема алгоритму метода Ейлера

    Схема алгоритму метода Ейлера для розв‘язання системи звичайних диференційних рівнянь наведена на рисунку 9.6.

        
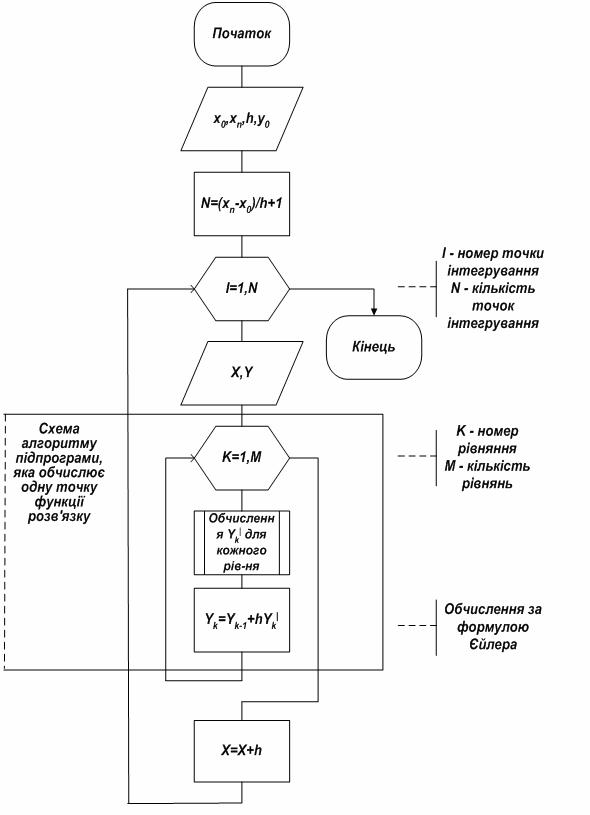
         Рисунок 9.6 – Схема алгоритму розв‘язання системи ЗДР методом Ейлера

         9.1.1 Модифікації методу Ейлера

    З метою підвищення точності методу Ейлера використовують різні його модифікації.

    Суть удосконаленого методу Ейлера полягає в використанні ітераційної формули виду:

    ,          (9.16)

    де - значення аргументу х в точці, а - значення функції в точці.

    Розглянемо диференціальне рівняння

              (9.17)

    з початковою умовою.

    Потрібно знайти розв’язок рівняння (9.13) на відрізку .

    Розіб'ємо відрізок на n рівних частин точками, де – крок інтегрування

    Алгоритм методу складається з:

    1. визначення похідної в точці :

    2. змінна х за формулою:

    3. визначення значення при

    4. визначення похідної в точці (,)

    5. використовуємо отримане значення для визначення за формулою:

    ,

    6. змінюємо

    7. повторюємо всі кроки алгоритму, починаючи з першого.

    Графічна інтерпретація методу представлена на рисунку 9.7.

        
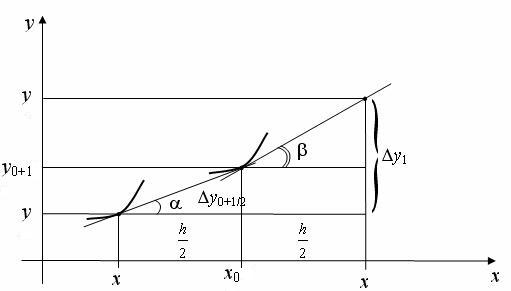
         Рисунок 9.7 – Графічна інтерпретація удосконаленого методу Ейлера

    Зауваження. Оцінка похибки в точці xі може бути отримана за допомогою "подвійного прорахунку": розрахунок повторюють із кроком h/2 похибка більш точного значення (при кроці h/2) оцінюють приблизно в такий спосіб:

                   (9.18)

    де у(х) - точний розв’язок диференціального рівняння. Удосконалений метод Ейлера є більш точним у порівнянні з методом Ейлера та відноситься до методів 3-го порядку точності.

    Схема алгоритму представлена на рисунку 9.8.

        

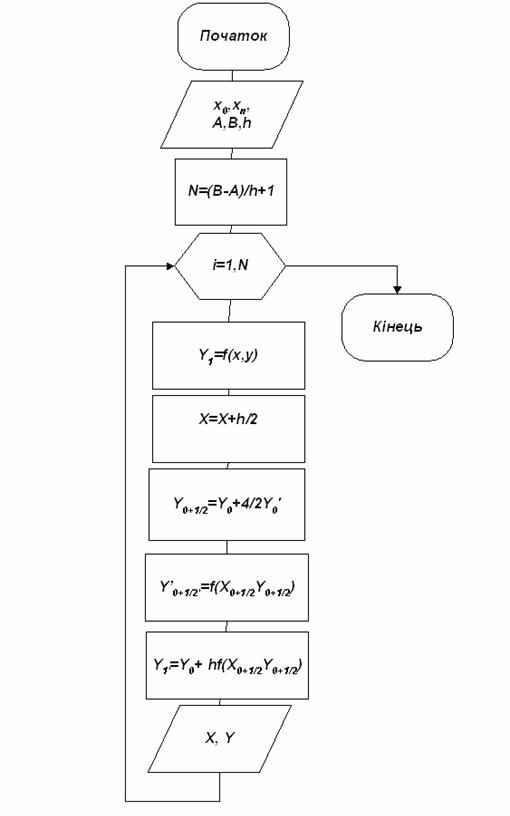
    Рисунок 9.8 - Схема алгоритму удосконаленого метода Ейлера

    Модифікований метод Ейлера заснований на використанні ітераційної формули виду:

                   (9.19)

    Геометрична інтерпретація представлена на рисунку 9.9.

        
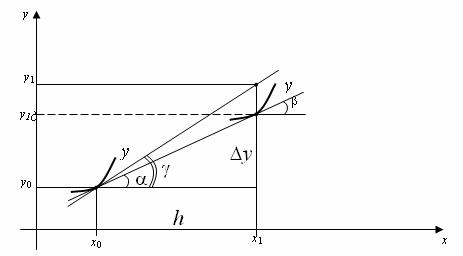
         Рисунок 9.9 – Графічна інтерпретація

    Алгоритм методу включає наступні кроки:

    1. визначення похідної в точці :

    2. зміна незалежної змінної х за формулою:

    3. визначення проміжного значення за формулою методу Ейлера

    4. визначення проміжної похідної в точці

    5. визначення середньо арифметичного значення двох похідних

    6. визначення у1 за формулою

    ітераційний процес повторюється, починаючи з першого кроку.

    Схема алгоритму метода представлена на рисунку 9.10.

        
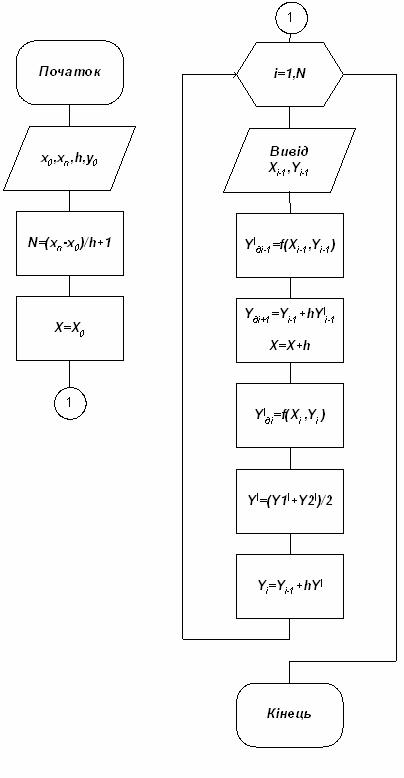
         Рисунок 9.10 - Схема алгоритму модифікованого метода Ейлера

    Удосконалений метод Ейлера - Коші з наступною ітераційною обробкою. Метод Ейлера - Коші з ітераційною обробкою є більш точним, чим, раніше розглянутий метод Ейлера - Коші. Сутність його полягає в тім, що виробляється ітераційна обробка кожного знайденого значення yі. Спочатку вибирається грубе наближення потім будується ітераційний процес:

                   (9.20)

    Ітерації продовжуються доти, поки два послідовних наближення не збіжаться до заданої похибки. Після цього приймається . Якщо після трьох-чотирьох ітерацій, при обраному значенні h, збігу потрібних знаків не відбувається, то варто зменшити крок розрахунку h.

         9.1.2 Метод Рунге–Кутта

    Метод Рунге-Кутта є одним з методів підвищеної точності, але має багато загального з методом Ейлера.

    Нехай на відрізку потрібно знайти чисельний розв’язок рівняння

              (9.21)

    з початковою умовою .

    Розіб'ємо відрізок на п рівних частин точками, де - крок інтегрування. В методі Рунге-Кутта, так само й у методі Ейлера, послідовні значення yі шуканої функції у визначаються по формулі

                   (9.22)

    Якщо розкласти функцію в у ряд Тейлора й обмежитися членами до h4 включно, то збільшення функції у можна представити у вигляді

              (9.23)

    де похідні визначаються послідовним диференціюванням з рівняння (9.4).

    Замість безпосередніх обчислень по формулі (9.23) у методі Рунге-Кутта визначаються чотири числа:

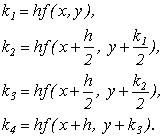              (9.24)

    Можна довести, що якщо числам k1, k2, k3, k4 додати відповідно вагу 1/6; 1/3; 1/3; 1/6, те середньозважене цих чисел, тобто

              (9.25)

    з точністю до четвертих ступенів дорівнює значенню у, обчисленому по формулі (9.23):

              (9.26)

    Таким чином, для кожної пари поточних значень xі і yі по формулах (9.24) визначаються значення

    По формулі (9.26) знаходиться

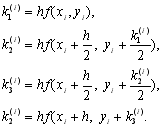              (9.27)

    і потім

    Числа k1, k2, k3, k4 мають простий геометричний зміст. Нехай крива M0CM1 (рис. 9.11) являє собою розв’язок диференціального рівняння (9.21) з початковою умовою (9.22). Точка С цієї кривої лежить на прямій, рівнобіжній осі Оу і розділяючою відрізок навпіл, В и G - точки перетинання дотичної, проведеної до кривої в точці М0, з ординатами АС і N1M1,. Тоді число k1 з точністю до множника h (де ) є кутовий

    коефіцієнт дотичної в точці М0 до інтегральної кривої M0CM1 тобто

    Точка В має координати , . Отже число k2 з точністю до множника є кутовий коефіцієнт дотичної, проведеної до ін тегральної кривої в точці В (BF - відрізок цієї дотичної).

        
         Рисунок 9.11 – Геометрична інтерпретація метода Рунге-Кутта

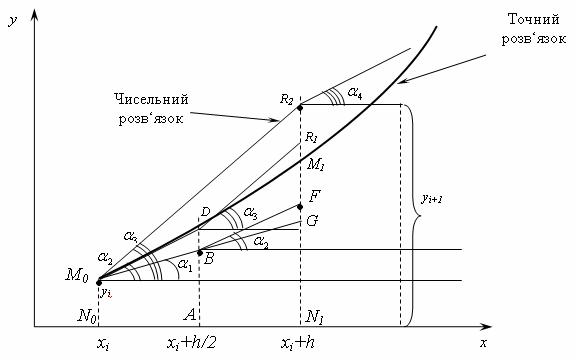
    Через точку М0 проведемо пряму, рівнобіжну відрізку BF. Тоді точка D має координати і k3 з точністю до множника h - кутовий коефіцієнт дотичної, перевіреної до інтегральної кривої в точці D (DR1 - відрізок цієї дотичної). Нарешті, через точку М0 проведемо пряму, рівнобіжну DR1, що перетне продовження M1N1 у точці .

    Тоді k4 з точністю до множника h є кутовий коефіцієнт дотичної, проведеної до інтегральної кривої в точці R2.

    Обчислення по методу Рунге-Кутта зручно розташовувати за алгоритмом,

    1. Значення х0 и у0 підставляють у праву частину диференціального рівняння (9.21), визначають.

    2. Отримане значення множать на крок інтегрування h, обчислюють

    .

    3. Змінюють значення х0

    4. визначають допоміжне значення

    5. визначення похідної в точці (,)

    6. визначають значення k2

    7. визначають нове допоміжне значення

    8. визначення похідної в точці (,)

    9. визначають значення k3

    10. визначають нове значення допоміжного у1д

    11. змінюють значення

    12. визначають допоміжну похідну в точці ()

    13. визначають значення k4

    14. визначають нове значення у1 за формулою

    Для визначення повторюють ітераційний процес, починаючи з першого кроку.

    Схема схема алгоритму метода Рунге-Кутта представлена на рисунку 9.12.

        
         Рисунок 9.12 – Схема алгоритму метода Рунге – Кутта

    Потім всі обчислення повторюють починаючи з І кроку, доти, поки не буде пройдений весь відрізок .

    Метод Рунге - Кутта має порядок точності h4 на усьому відрізку . Оцінка точності методу цього дуже складна. Грубу оцінку погрішності можна одержати за допомогою "подвійного прорахунку" по формулі

                   (9.28)

    де - значення точного розв’язку рівняння (9.21) у точці наближені значення, отримані з кроком h/2 і h. Якщо - задана точність розв’язку, то число п (число розподілів) для визначення кроку інтегрування вибирається таким чином, щоб

              (9.29)

    Однак крок розрахунку можна змінювати при переході від однієї точки до іншої.

    Для оцінки правильності вибору кроку h використовують рівність

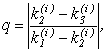              (9.30)

    де q повинно бути дорівнює декільком сотим, у противному випадку крок h зменшують.

    Нехай задана система диференціальних рівнянь першого порядку:

              (9.31)

    У цьому випадку паралельно визначаються числа

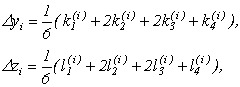              (9.33)

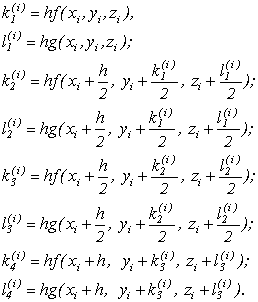              (9.34)

    Тоді одержимо розв’язок системи диференційних рівнянь другого порядку:

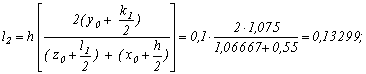
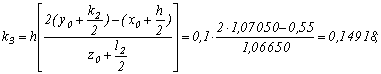
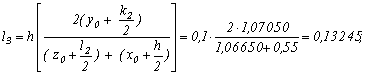
    Отже,

    і остаточно одержуємо значення шуканих функцій у точці х = 0,6:

    Приклад 9.1. Розв’язати на ЕОМ систему рівнянь виду:

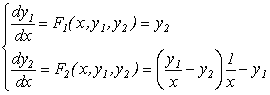
    При розробці програми для розв‘язку системи диференційних рівнянь, створюють: 1) підпрограму, яка містить праві частини рівнянь; 2) підпрограму, яка реалізує алгоритм метода Рунге-Кутта для обчислення значень функцій системи в одній точці; 3) підпрограму, яка дозволяє отримати розв‘язок системи на заданому відрізку дослідження. Наприклад, підпрограму, яка містить дану систему можна записати на алгоритмічній мові С у вигляді:

    void systema (float *Y, float *F, float X)

    { ;

    ;

    }

    де - значення правої частини рівняння заданої системи.

    Приклад 9.2. Розглянемо приклад розв’язання відомої інженерної задачі на ЕОМ за допомогою методу Рунге-Кутта.

    З задачами про удар і коливання часто стикаються в аерокосмічній промисловості і на транспорті, де існують багато численні джерела коливань. Видалення ударних й вібраційних навантажень має виключно велике значення для забезпечення нормальної роботи приборів й систем управління й створення комфортних умов для екіпажу. Звичайно для захисту від великих вібрацій в конструкцію транспортного засобу вводять пружні опори, що забезпечені пристроями, що забезпечують деяке демпфіроване коливання. Такі опори різко зменшують частоти власних коливань конструкції, забезпечуючи їх суттєву відмінність від частот збуджуючих силових факторів. Такий розв’язок ефективний як засіб захисту від стаціонарних коливань, однак в випадку ударних навантажень піддатливість опор може призвести до недопустимо великих зміщень.

        
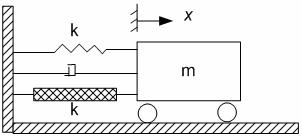
         Рисунок 9.13 – Графічне представлення використання пружних опор в транспортних засобах

    Відомо, що від цього недоліку вільні системи підвіски, в яких використовуються пружини з симетричною нелінійною характеристикою жорсткість яких прогресивно збільшується при більших відхиленнях от робочої точки.

    Пристрій, показаний на рисунку 9.13, складається з маси т, зв'язаною з жорсткою стінкою через пружину постійної жорсткості k, демпфер з коефіцієнтом демпфірування с й пружиною з нелінійною характеристикою утворюючої відновлюючу силу, рівну добутку постійної k на зміщення в третій степені. Така пружина має симетричну нелінійну характеристику, забезпечуючи захист від ударних й вібраційних навантажень. Так як рух цієї системи описується нелінійним диференціальним рівнянням:

    ,

    то традиційні «точні» методи не дозволяють знайти залежність зміщення х від часу. Тому для розв'язку вказаного рівняння прийдеться скористатись чисельним методом. Нехай параметри системи мають наступні значення:

    k=2,0 Н/см; k* = 2, 0 Н/см3; с = 0,15 Нс/см; m=1,0 кг,

    а початкові умови задані в вигляді: х(0) - 10 см, х(0)=0.

    Підготуємо й реалізуємо на ЕОМ програму для моделювання руху даної механічної системи в інтервалі часу 0 t 1 .

    Щоб розв'язати цю задачу однокроковим чисельним методом, необхідно звести диференціальне рівняння другого порядку до двох диференціальних рівнянь першого порядку за допомогою допоміжної змінної , . В результаті отримаємо:

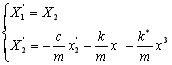
    Щоб при видачі довжина виражалась в сантиметрах, змінимо розмірністьмаси. Тоді m=0,01 Н?с2 /см.

        
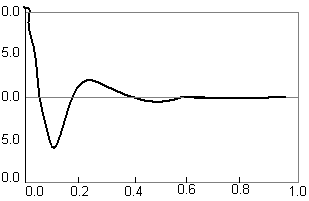
         Рисунок 9.14 – Графік представлення результатів чисельного розв’язку приклада 9.11 на ЕОМ

    З приведеного графіка залежності зміщення від часу видно, що частота коливань залежить від амплітуди. Саме так звичайно і ведуть себе нелінійні системи, що мають пружини, жорсткість яких при стискові збільшується.

         9.4 Методи прогнозу і корекції (багатоточкові методи)

    В методах прогнозу і корекції для обчислення значення нової точки розв‘язку ДР використовується інформація про декілька раніше отриманих точок відрізку дослідження. Для цього використовуються дві формули, що називаються відповідно формулами прогнозу і корекції. Схеми алгоритмів для всіх таких методів майже однакові, а самі методи відрізняються лише формулами. На рис. 9.15 представлена схема алгоритму методу прогнозу і корекції для розв’язку диференціального рівняння виду:

              (9.35)

        
         Рисунок 9.15 – Схема алгоритму багатоточкового методу

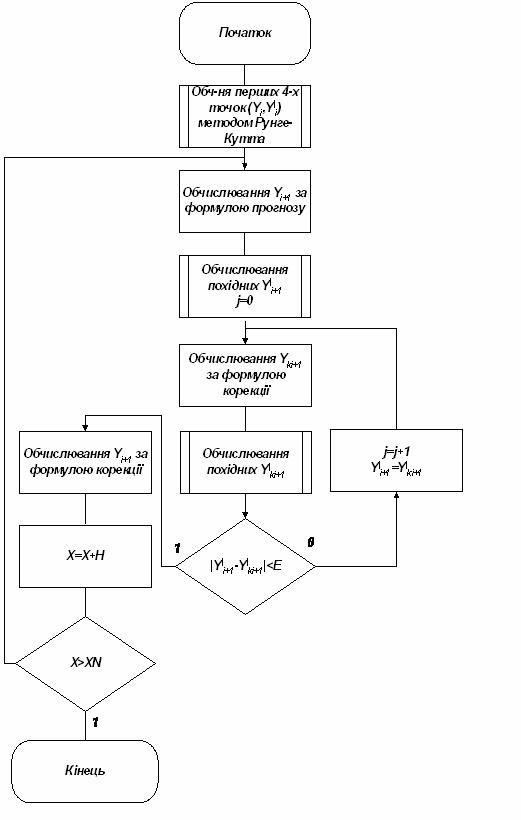
    Розглянемо особливості алгоритмів методів прогнозу і корекції.

    Так як в методах, що розглядаються використовується інформація про декілька раніше отриманих точок, то на відміну від однокрокових методів вони не володіють властивістю „самостартування”. Тому, перед тим як застосовувати метод прогнозу і корекції, необхідно обчислювати вихідні данні за допомогою якого-небудь однокрокового методу. Часто для цього використовують метод Рунге-Кутта. Обчислення проводять наступним чином. Спочатку по формулі прогнозу і початковим значенням змінних знаходять значення . Верхній індекс (0) означає, що прогнозоване значення є одним з послідовності значень , що розташовані в порядку зростання точності. По прогнозованому значенню за допомогою приведеного вище диференціального рівняння знаходять похідну

              (9.36)

    яка потім підставляється у формулу корекції для обчислення уточненого значення .

    В свою чергу використовується для отримання більш точного значення похідної за допомогою диференціального рівняння

         .     (9.37)

    Якщо це значення похідної недостатньо близьке до попереднього, то воно вводиться у формулу корекції й ітераційний процес продовжується. Якщо ж похідна змінюється в допустимих границях, то значення використовується для обчислення остаточного значення , яке і видається на друк. Після цього процес повторюється – здійснюється наступний крок, на якому обчислюється .

    Звичайно при вводі формул прогнозу і корекції розв’язок рівняння розглядають як процес наближеного інтегрування, а самі формули отримують за допомогою кінцево-різницевих методів.

    Якщо диференціальне рівняння про інтегровано в інтервалі значень від до , то результат прийме вигляд

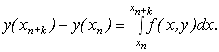              (9.38)

    Цей інтеграл не можна обчислити безпосередньо, так як залежність заздалегідь невідома. Наближене значення інтегралу можна знайти за допомогою одного з кінцево-різницевих методів. Вибір методу і буде визначати метод розв’язку диференціальних рівнянь. На етапі прогнозу можна використовувати будь-яку формулу чисельного інтегрування, якщо до неї не входить попереднє значення .

         9.4.1 Метод Мілна

    В цьому методі на етапі прогнозу використовується формула Мілна

              (9.39)

    а на етапі корекції - формула Сімпсона

              (9.40)

    Останні члени в обох формулах в дійсності в ітераційному процесі не використовуються і слугують лише для оцінки помилки відсічення. Метод Мілна відносять до методів четвертого порядку точності, так як в ньому відкидаються члени, які містять h п’ятій степені і більш високих степенях. Може виникнути питання навіщо потрібна корекція, якщо прогноз дає четвертий порядок точності. Відповідь на це питання дає оцінка відносної величини членів, що виражають похибку. В даному випадку похибка відсічення при корекції в 28 разів менше і тому представляє великий інтерес. Незважаючи на те що формула Мілна містить менший числовий коефіцієнт (1/90) перед членом, що відкидається, її використовують рідше, ніж інші (з більшими відкидуваними членами), так як їй притаманна нестійкість. Це означає, що похибка поширення може рости експоненціально, при чому цей висновок справедливий для всіх формул корекції, основаних на правилі Сімпсона.

         9.4.2 Метод Адамса - Башфорта

    Цей метод також має четвертий порядок точності. Формула, що використовується в ньому отримана інтегруванням оберненої інтерполяційної формули Ньютона і має вид

              (9.41)

    На етапі корекції використовується формула

              (9.42)

    Розрахунки по методу Адамса - Башфорта виконуються так як і по методу Мілна, але на відміну від останнього похибка, внесена на якому-небудь кроці, не має тенденції до експоненціального росту.

    Можна припустити, що так як величина відкиненого члену відома, то її можна використовувати для уточнення скоректованого значення залежної змінної. Так як внесення поправок в корегуючий член може негативно вплинути на стійкість рахунку, то для підвищення точності рахунку слід використовувати методи більш високих порядків точності.

         9.4.3 Метод Хемінга

    В методі Хемінга використовуються наступні формули:

                   (9.43)

    уточнення прогнозу

                   (9.44)

                   (9.45)

    корекції

              (9.46)

    Це стійкий метод четвертого порядку точності, в основі якого лежать наступні формули прогнозу:

              (9.47)

    і корекції

              (9.48)

    Особливістю методу Хемінга є те, що він дозволяє оцінювати похибки, що вносяться на стадіях прогнозу і корекції і усувати їх. Завдяки простоті та стійкості цей метод є одним з найбільш поширених методів прогнозу і корекції.

         Література

    1. Фельдман Л.П., Петренко А.І. Дмитрієва О.А. Чисельні методи в інформатиці: Підручник/ За ред. М.З. Згуровського. – К.: Вид. група BHV, 2006. – 480 с.

    2. Мак – Кракен Д., Дрон У. Численные методы и програмирование на фортране. – М.: Мир, 1977. – 584 с.

    3. Бахвалов Н. С. Численные методы . Т. И. Анализ, алгебра, обычные диференциальные уравнения. – М.: Наука, 1975. – 631 с.

    4. Ляшенко М.Я., Головань М.С. Чисельні методи: Підручник. Либідь. 1996. – 288 с.

    5. Численные методы / Н. И. Данилина, Н. С. Дубровская, О. П. Кваша и др. – М.: Высшая шк., 1976. – 368 с.

    6. Ракитский Ю. В., Устинов С. М., Черноруцкий И. Т. Численные методы решения жестких систем. – М.: Наука, 1979. – 587 c.

    7. Плис А.И., Сливина Н.А. Mathcad. Математический практикум для инженеров и экономистов: – М.: Финансы и статистика, 2003. – 656с.

    8. Д. Мэтьюз, Г. Цинк, Д. Куртис. Численне методы. Использование Matlab, –М. Издательский дом “Вильямс”, 2001. – 720 с. 720 с.

    9. Иванов В. В. Методы вычислений на ЕОМ. – Киев: Наук. думка, 1986. – 584 с.

    10. Маліков В.Т., Кветний Р.Н. Вычислительные методы и применение ЭВМ. – К.: Высшая школа., 1989. – 213 с.

    11. Квєтний Р.Н. Методи комп’ютерних обчислень: Навчальний посібник. /МО І науки України. – Вінниця: ВДТУ, 2001. – 148 с.

    12. Ортега Дж., Пуп У. Введение в численные методе решения диференциальных уравнений. – М.:Наука,1986. – 288 с.

    13. Молчанов И. М. Машинные методы решения прикладных задач, диф. уравнений. – Киев: Наук. Думка, 1988. – 344 с.

    14. Прикладные методы и программирование в численном анализе. – М.: Изд-во Моск. ун – ту, 1985. – 185 с.

         Питання та задачі до самостійної роботи

    1. Яке рівняння називається диференціальним?

    2. Яке рівняння відноситься до звичайного?

    3. Яке рівняння відноситься до рівняння з частковими похідними?

    4. Що таке задача Коші?

    5. Яка задача відноситься до краєвої?

    6. Що таке початкові умови?

    7. Що таке краєві умови?

    8. Які методи відносяться до одноточкових?

    9. Які методи відносяться до багатоточкових?

    10. Які методи відносяться до методів прогнозу і корекції?

    11. Особливість математичної моделі методу Ейлера.

    12. Геометрична інтерпретація методу Ейлера.

    13. Алгоритм методу Ейлера.

    14. Математична модель модифікованого методу Ейлера.

    15. Геометрична інтерпретація модифікованого методу Ейлера.

    16. Алгоритм модифікованого методу Ейлера.

    17. Математичні моделі удосконаленого методу Ейлера.

    18. Геометрична інтерпретація удосконаленого методу Ейлера та методу Ейлера.

    19. Алгоритм удосконаленого методу Ейлера.

    20. Математична модель методу Рунге-Кутта.

    21. Геометрична інтерпретація методу Рунге-Кутта.

    22. Алгоритм методу Рунге-Кутта.

    23. Особливості чисельних методів розв’язання СИДР з автоматичною зміною кроку.

    24. Узагальнений алгоритм багатоточкових методів.

    < Зміст >