, (8.1)
Метод Ньютона-Котеса засновано на інтерполяції однієї із сторін криволінійних трапецій, що отримані поділом відрізку інтегрування [а,b] на N рівних частин, багаточленами більш високих порядків ніж в методі трапецій (де використовується лінійна інтерполяція) і в методі Сімпсона (де використовується квадратична інтерполяція).
Основна формула методу Ньютона-Котеса має вигляд:
, (8.1)
де 
- значення підінтегральної функції f(x) в вузлах інтерполяції, Hi – коефіцієнти Ньютона-Котеса, які не залежать від вигляду підінтегральної функції f(x), а залежать тільки від N (кількості вузлів інтерполяції), тому значення їх для різної кількості вузлів відомі та представлені в таблиці 8.1. Можна показати, що методи трапецій та Сімпсона є частинними випадками методу Ньютона-Котеса.
Таблиця 8.1 - Коефіцієнти Ньютона-Котеса
На відміну від методу Ньютона-Котеса, в якому коефіцієнти Hi (i=1,N) знаходять у фіксованих вузлах інтерполяції, П.Л. Чебишев запропонував для обчислення визначених інтегралів використати формулу
, (8.2)
в якій квадратурні коефіцієнти Сi (і=1,2,…,N) зафіксовані, а абсциси xi (і=1,2,…,N) підлягають визначенню. Для простоти обчислень необхідно вибрати С1=С2=…=Сn. Розглянемо спочатку частинний випадок, коли межі інтегрування дорівнюють –1 та 1. Тоді попередня формула набере вигляду
, (8.3)
де квадратурні коефіцієнти Сn та абсциси xi підлягають визначенню.
Коефіцієнти Сi та вузли інтерполяції xi визначимо із умови, що ця рівність є точною для випадку, коли f(х) - багатогочлен вигляду
(8.4)
Підставимо багаточлен (8.4) у ліву частину (8.3) та проінтегруємо:
(8.5)
У праву частину рівності (8.3) підставимо значення многочлена (8.4) у вузлах х1, х2, …,хn:
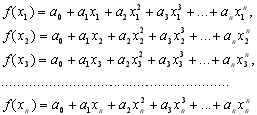(8.6)
Тоді формула (8.5) буде мати вигляд
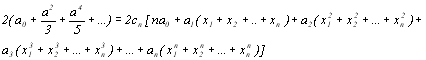(8.7)
Отримана рівність повинна виконуватися за будь-яких значень аo,а1,…,аn і таким чином, порівнюючи коефіцієнти аi в правій і лівій частинах (8.7) знаходимо, що nCn=1, звідки
(8.8)
i, крім цього,
(8.9)
Підставляючи знайдене для Сn виразу в співвідношення (8.5) отримаємо формулу Чебишева:
(8.10)
де точки x1,…,xn визначаються із системи рівнянь (8.9).
Значення x1,…,xn для різних n відомі та представлені в таблиці 8.2.
Таблиця 8.2 - Значення абсцис для різної кількості точок
Коли межі даного інтеграла відрізняються від –1 та 1 , формула Чебишева матиме вигляд
, (8.11)
де
. (8.12)
а xi мають вказані в таблиці значення.
Для отримання підвищеної точності для чисельного інтегрування користуються формулою Гауса
, (8.13)
в якої не фіксуються не тільки вузли інтерполяції x1, x2,…,xn, а й квадратурні коефіцієнти С1,…,Сn. При цьому Zn невідомих величин x1,…,xn; С1,…,Сn визначається із умови, що формула є точною у випадку будь-якого багаточлена 2n-1.
Таким чином, для будь-якого багаточлена (2n-1)-й степеню
(8.14)
повинна виконуватися рівність:
. (8.15)
Багаточлен f(x) степеню 2n-1 можна показати у вигляді
f(x)=F(x)Q(x)+R(x) , (8.16)
де F(x)-шуканий багаточлен n-ї степені, а Q(x) та R(X)- відповідно частинне ділення f(x) на F(x) та залишок від цього ділення, степінь багаточленів Q(x) та R(x) не перевищують (2n-1).
Вираз для F(x) можна записати так:
(8.17)
тут величини x1,…,xn - шукані абсциси формули Гаусса, а А1,А2,…,Аn - постійні.
Оскільки шукана функція F(x) у вузлах x1,…,xn перетворюється на нуль, то
(8.18)
(8.19)
Але для багаточлена R(x) степеню не вище n-1 також повинна виконуватися рівність:
(8.20)
Bіднімаючи (8.20) від (8.19),отримаємо
Із останнього відношення можна визначити шукану функцію F(x). Оскільки ця рівність справедлива для якого-небудь багаточлена Q(x) степеню n-1
, (8.21)
то при будь-яких коефіцієнтах 
маємо таку систему рівнянь:
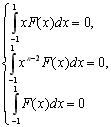(8.22)
Підставляючи в (8.22) вирази для F(x) із формули (7.2 ) та інтегруючи, отримаємо для визначення коефіцієнтів А1, … Аn систему n рівнянь
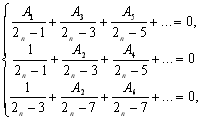(8.23)
з яких видно, що А1=А3=А5=А7=…=0 та, отже, шуканий многочлен має вигляд:
(8.24)
Відмітимо, що при парному n корені рівняння F(x)=0 попарно рівні за абсолютним значенням, але протилежні за знаком, а при непарному n коренем є також і х=0.
Визначивши із системи (8.23) коефіцієнти Аі (і=1,2,…,n), складемо рівняння F(x)=0 та знайдемо його корені х1,…,хn, тобто шукані абсциси формули Гаусса, а потім обчислимо коефіцієнти Сi (і=1,2,…,n) за формулою
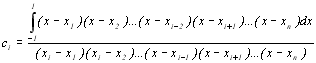(8.25)
Приклад 1. Побудувати квадратурну формулу Гаусса для випадку n=2 на відрізку інтегрування [-1, 1].
Розв‘язок. Загальний вигляд квадратурної формули Гаусса при n=2 та заданих межах інтегрування:
,
де підлягають визначенню квадратурні коефіцієнти с1 та с2, а також абсцис х1 та х2.
Для визначення абсцис складемо многочлен 
, коефіцієнти А1 та А2 якого знайдемо із системи вигляду (8.22)
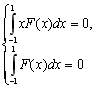
підстановкою багаточлена F(x) у систему. Маємо
; 
,
тобто А1=0, А2 =-1/3. Тоді 
, звідки
та 
Коефіцієнти с1 та с2 обчислимо за формулою (8.25)
; 
Отже, 
Для обчислення інтеграла загального вигляду 
слід замінити змінні
, (i=1,2,….,n) (8.26)
Тоді формула Гаусса прийме вигляд
Значення квадратурних коефіцієнтів Гаусса сі (і=1,2...n) та абсцис хі (і=1,2...n) наведені в таблиці 8.3.
Таблиця 8.3 – Значення квадратурних коефіцієнтів Гаусса
n=1 |
x1=0,5 |
с1=2 |
n=2 |
-x1=x2=0,577350 |
с1=с2=1 |
n=3 |
-x1=x3=0,774597, x2=0 |
с1=с3=0,555555, с2=0,888889 |
n=4 |
-x1=x4=0,861136, -x2=x3=0,339981 |
с1=с4=0,347855, с2=с3=0,652145 |
n=5 |
-x1=x5=0,906180, -x2=x4=0,538470 |
с1=с5=0,236927, с2=с4=0,478629 |
n=6 |
-x1=x6=0,932470, -x2=x5=0,661210, -x3=x4=0,238620 |
с1=с6=0,171324, с2=с5=0,360761, с3=с4=0,467914 |
n=7 |
-x1=x7=0,949108, -x2=x6=0,741531, -x3=x5=0,405845, x4=0 |
с1=с7=0,129485, с2=с6=0,279705, с3=с5=0,381830, с4=0,417960 |
n=8 |
-x1=x8=0,960290, -x2=x7=0,796666, -x3=x6=0,525532, x4=0,183434 |
с1=с8=0,101228, с2=с7=0,222381, с3=с6=0,313707, с4=с5=0,362684, |
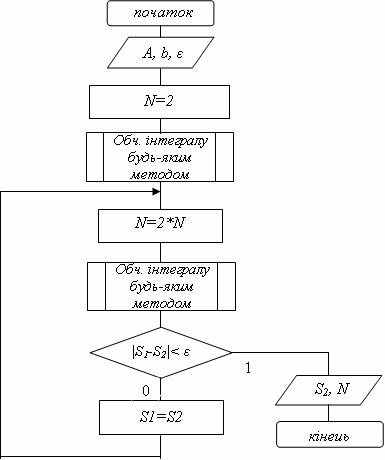
Більшість вище розглянутих методів основані на використанні кількості точок N, на які розбивається відрізок інтегрування. Але при розв’язанні реальних інженерних задач, що потребують визначення інтегралу на ЕОМ, достатньо складно визначити оптимальне для нього значення N. Тому в багатьох пакетах прикладних програм використовують наступний загальний алгоритм обчислення визначеного інтегралу (рис.8.1), що автоматично визначає кількість точок N в залежності від заданої похибки обчислень 
. Особливістю даного алгоритму є те, що для обчислення інтегралу можна використовувати будь-який з відомих вам методів.
1. Щуп Т. Решение инженерных задач на ЭВМ. – М.: Мир, 1982. – 235с.
2. Демидович Б. П., Марон И. А. Основы вычислительной математики. – М.: Наука, 1970. – 664 с.
3. Форсайт Дж., Малькольм., Моулер Р. Машинные методы математических вычислений. – М.: Мир, 1980.
4. Ляшенко М.Я., Головань М.С. Чисельні методи: Підручник. Либідь. 1996. – 288 с.
5. Крылов В. И., Шульга А. Т. Справочная книга по численному интегрированию. – М.: Наука, 1966.
6. Хемминг Р. В. Численные методы. – М.: Наука, 1972. – 399 с.
7 Плис А.И., Сливина Н.А. Mathcad. Математический практикум для инженеров и экономистов: – М.: Финансы и статистика, 2003. – 656с.
1. 8. Крилов В. И. и др. Начала теории вычислительных методов. Интегральное уравнение, некорректные задачи и улучшение сходимости. – Минск: Наука и техника, 1984. – 263 с.
9. Прикладные методы и программирование в численном анализе. – М.: Изд-во Моск. ун – ту, 1985. – 185 с.
1. Особливість алгоритму методу Чебишова. В яких випадках рекомендують застосовувати цей метод?
2. Особливість алгоритму методу Гаусса.
3. Особливість алгоритму методу Ньютона – Котеса. В яких випадках слід застосовувати цей метод?
4. Як можна поставити експеримент на дослідження інтеграла, в основі якого лежить дуже осцилююча функція типу 
?
5. Обчислити інтеграл 
, приміняючи квадратурну формулу Гаусса з чотирма ординатами.
6. За допомогою формули Чебишева обчислити 
, де 
.