:Інженеру часто приходиться обчислювати визначений інтеграл чисельними методами. Це буває у тих випадках, коли або не вдається виразити інтеграл у замкненій формі, або вона настільки складна, що простіше скористатися чисельним інтегруванням. Чисельне інтегрування являє собою стійкий процес і в протиставлення чисельному розв’язанню диференційних рівнянь зменшує дію похибок у початкових даних на кінцевий результат.
Розглянемо функцію f(x), що визначена на відрізку [a,b]. Функція, що диференціюється на відрізку [a,b] функцією F(x), похідна якої в кожній точці [a,b] дорівнює f(x), називається первісною функції f(x) та записується як:
F’(x)= f(x).
Так як (F(x)+С)’=F’(x)=f(x) для будь-якої сталої С, то можна говорити про множину первісних – множину функцій виду F(x)+С. Множина первісних F(x)+С функції f(x) називається невизначеним інтегралом функції f(x) і позначається :
,
де F(x)+С – значення невизначеного інтегралу, тобто множини первісних функції f(x):
(
)’=(F(x)+С)’= f(x).
Розглянемо функцію f(x), що визначена на відрізку [a,b]. Розіб’ємо відрізок [a,b] на n довільних частин точками a=x0< x1< x2<…< xn-1< xn=b
і позначимо 
i=1,...,n, 
.
На кожному відрізку [xi-1, xi ] візьмемо довільну точку 
i і обчислимо в неї значення функції f(x). Вираз
називається інтегральною сумою функції f(x). Якщо при 
існує границя 
, не залежна ні від способу розбиття відрізку [a,b] точками xi, i=1,2,…,n-1, ні від вибору точок 
i
(xi1, xi), то ця границя називається визначеним інтегралом від функції f(x) на відрізку [a,b] , а саму функцію – інтегрованою на [a,b], та позначають як
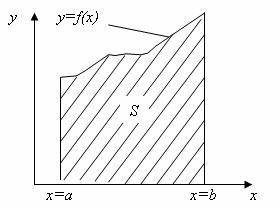
Розглянемо геометричний зміст визначеного інтегралу: якщо f(x)>0, то 
дорівнює площі фігури , обмеженої графіком функції, віссю абсцис і прямими 
і 
(рис.7.1).
В основу чисельного інтегрування покладене наближене обчислення площини під кривою, яка описується підінтегральною функцією інтеграла виду
.
Розглянемо загальний підхід до розв'язування цієї задачі на ЕОМ.
Визначений інтеграл І являє собою площину, обмежену кривою f(x), віссю х та прямими х = a; х = b (рис.7.1).
Чисельне інтегрування основане на тому, що відрізок інтегрування [a,b] розбивають на n менших відрізків [xi-1, xi ] , кожен з яких є основою геометричної фігури, площу якої знаходять наближено як Si, а значення інтегралу І визначають як суму таких площин Si, тобто
.
При цьому використовують два способи розбиття відрізка інтегрування на менші :
1. Розбиття відрізка інтегрування проводиться раніше аналізу результатів інтегрування, до того ж завжди відрізки вибирають рівними (метод прямокутників, трапецій, Сімпсона);
2. Місцезнаходження та довжина відрізків визначаються з умови досягти найбільшої точності чисельного інтегрування з заданим числом відрізків, а потім відповідно з цим визначають їхні межі (метод Гаусса, Ньютона-Котеса, Чебишева ).
Розглянемо відомі чисельні методи знаходження визначених інтегралов на ЕОМ.
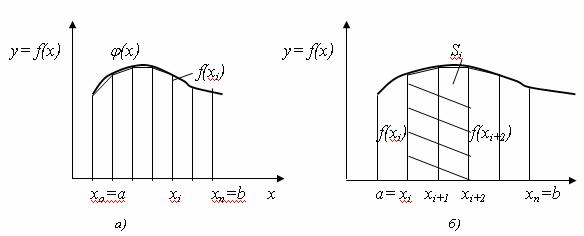
Найпростіший метод наближеного обчислення інтеграла на ЕОМ є метод прямокутників, суть якого зводиться до знаходження визначеного інтегралу як суми площ N прямокутників (з висотою f(x) та основою 
), отриманих шляхом розбиття відрізка інтегрування [а, b] на N рівних частин. В цьому випадку розділити на прямокутники можна або зліва на право (рис.7.2,а), тоді отримаємо формулу лівих прямокутників (7.1), або справа наліво (рис.7.2,б), тоді отримаємо формулу правих прямокутників (7.2):
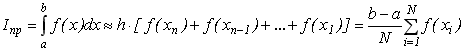(7.1)
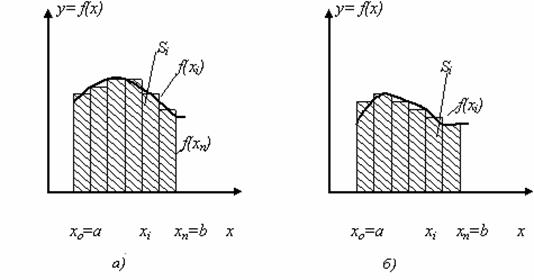
(7.2)
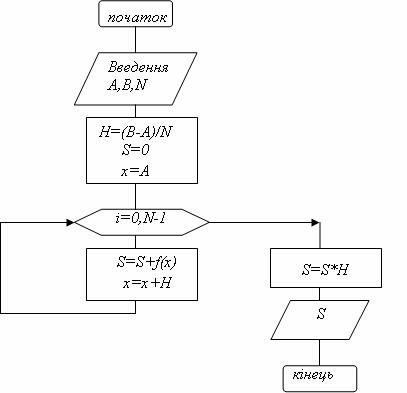
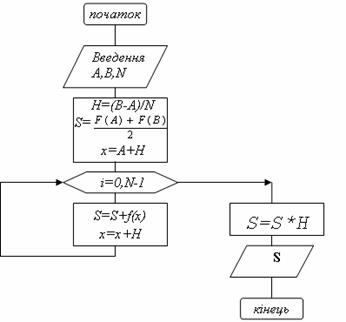
Схема алгоритму обчислення визначеного інтегралу методом прямокутників показана на рис. 7.3.
Суть методу трапецій полягає в тому, що інтеграл обчислюється таким чином: відрізок інтегрування [а, b] поділяється на N рівних відрізків, всередині яких підінтегральна крива f(x) замінюється кусково-лінійною функцією j(х), отриманою стягуванням ординат N відрізків [xi-1, xi ] хордами.
Інтеграл знаходиться як сума площ Si прямокутних трапецій (pис.7.4 а,б).
Площа кожної такої трапеції визначається як
.
Відповідно на всьому відрізку інтегрування [а, b] площа складної фігури, яка визначається як сума площин всіх таких трапецій, визначається формулою:
.
Оскільки в даної формулі під знаком суми величини 
зустрічаються двічі, тому її можна переписати у вигляді:
(7.3)
Похибка обчислення інтеграла за формулою трапеції визначається:
(7.4)
Схема алгоритму обчислення інтегралу методом трапецій показано на рис. 7.5.
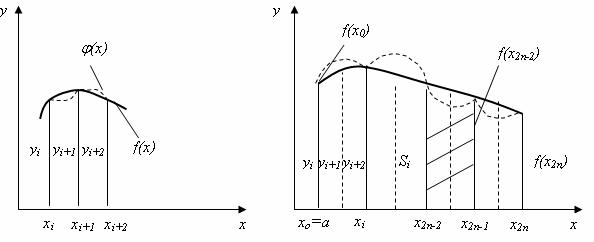
У цьому методі інтегрування проводиться шляхом поділу відрізка [а,b] на N пар відрізків та, з метою збільшення точності наближеного інтегрування на кожному такому відрізку 
, підінтегральна функція f(x) замінюють квадратичною параболою j(х) (рис. 7.6 а,б), і обчислення визначеного інтеграла зводиться до обчислення суми площин N криволінійних трапецій Si :
Площа кожної такої криволінійної трапеції визначається за формулою Сімпсона:
(7.5)
Визначимо за формулою (7.5) площину N криволінійних трапецій Si :
(7.6)
Тоді сума всіх криволінійних трапецій визначається як
або 
, (7.7)
де 
, тобто кількість відрізків повинна бути парною.
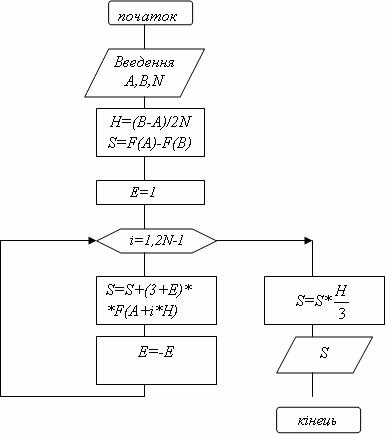
Схема алгоритму обчислення визначеного інтегралу методом Сімпсона, запропонована Делем В.Д., представлена на рис. 7.7.
1. Щуп Т. Решение инженерных задач на ЭВМ. – М.: Мир, 1982. – 235с.
2. Демидович Б. П., Марон И. А. Основы вычислительной математики. – М.: Наука, 1970. – 664 с.
3. Форсайт Дж., Малькольм., Моулер Р. Машинные методы математических вычислений. – М.: Мир, 1980.
4. Ляшенко М.Я., Головань М.С. Чисельні методи: Підручник. Либідь. 1996. – 288 с.
5. Крылов В. И., Шульга А. Т. Справочная книга по численному интегрированию. – М.: Наука, 1966.
6. Хемминг Р. В. Численные методы. – М.: Наука, 1972. – 399 с.
7 Плис А.И., Сливина Н.А. Mathcad. Математический практикум для инженеров и экономистов: – М.: Финансы и статистика, 2003. – 656с.
1. 8. Крилов В. И. и др. Начала теории вычислительных методов. Интегральное уравнение, некорректные задачи и улучшение сходимости. – Минск: Наука и техника, 1984. – 263 с.
9. Прикладные методы и программирование в численном анализе. – М.: Изд-во Моск. ун – ту, 1985. – 185 с.
1. На чому базується загальний підхід до чисельного інтегрування?
2. Особливість алгоритму методу прямокутників.
3. Особливість алгоритму методу трапецій. Як оцінити похибку отриманих результатів?
4. Алгоритм методу Сімпсона. Як оцінити похибку отриманих результатів?
5. В чому особливість квадратурних методів обчислення визначеного інтегралу на ЕОМ?
6. В яких випадках використовуються поліноміальні методи обчислення визначеного інтегралу на ЕОМ?