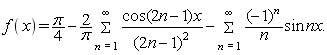Інженеру звичайно приходиться працювати з великими масивами даних, тому методи обробки числових даних мають для нього особливе значення. Часто шляхом к правильному розумінню багатьох задач служить продумане уявлення початкових даних. До речі невдале уявлення експериментальних даних буває причиною помилок в розв’язанні складних задач.
Для того щоб отримати аналітичні залежності, що описують великі масиви даних, використовують методи апроксимації, які основані на тому, що масив даних замінюють простою функцією (лінійною або квадратичною або кубічною або іншою), яка не обов’язково проходить через всі експериментальні точки, але описує тенденції зміни цих даних та забезпечує мінімум суми квадратів відхилень експериментальних даних від цією функції.
Постановка задачі
Припустимо, що в результаті інженерного або наукового експерименту отримана система точок ![]() . Необхідно знайти аналітичну залежність
. Необхідно знайти аналітичну залежність ![]() , таку, яка найкращим чином описує задану систему точок. Поняття "найкращим чином" означає розв’язання задачі по заданому критерію. Найбільш відомим критерієм для задач апроксимації є критерій середньоквадратичних відхилень (СКВ), який являє собою мінімізацію суми квадратів відхилень експериментальних даних від аналітичної функції
, таку, яка найкращим чином описує задану систему точок. Поняття "найкращим чином" означає розв’язання задачі по заданому критерію. Найбільш відомим критерієм для задач апроксимації є критерій середньоквадратичних відхилень (СКВ), який являє собою мінімізацію суми квадратів відхилень експериментальних даних від аналітичної функції ![]() і визначається на заданій множині точок як
і визначається на заданій множині точок як
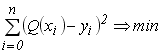 .
.
Однак при такій постановці задача апроксимації експериментальних даних має багато розв’язків. Для отримання єдиного розв’язку цієї задачі потрібно задавати значення ![]() певного вигляду, наприклад:
певного вигляду, наприклад:
![]() ; (6.1)
; (6.1)
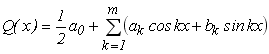 ; (6.2)
; (6.2)
![]() ; (6.3)
; (6.3)
Розглянемо загальні математичні моделі, які можна отримати при апроксимації табличних функцій степеневим поліномом.
Постановка задачі
В результаті інженерного або наукового експерименту отримана система точок ![]() . Необхідно знайти степеневий поліном виду:
. Необхідно знайти степеневий поліном виду:
![]() , (6.4)
, (6.4)
такий, щоб сума квадратів відхилень полінома ![]() від заданої системи експериментальних точок була би мінімальною. Така задача зводиться до визначення коефіцієнтів поліному
від заданої системи експериментальних точок була би мінімальною. Така задача зводиться до визначення коефіцієнтів поліному ![]() . Метод, що дозволяє розв’язати її називається методом найменших квадратів (МНК). Критерій середньо квадратичного відхилення (СКО) в даному випадку має вигляд:
. Метод, що дозволяє розв’язати її називається методом найменших квадратів (МНК). Критерій середньо квадратичного відхилення (СКО) в даному випадку має вигляд:
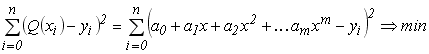 (6.5)
(6.5)
Розглянемо рисунок 6.1.
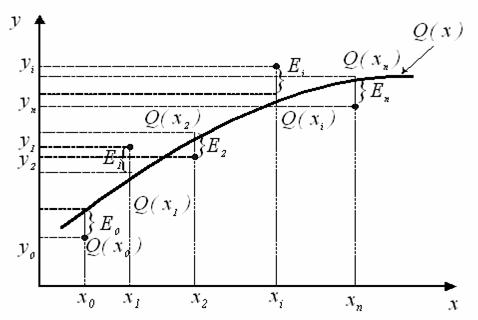
З нього видно, що
![]() ,
, ![]() , ...,
, ..., ![]() ,
,
тому вираз (6.5) можна представити в вигляді:
![]()
Очевидно, що функція E - це багато параметрична функція на множині ![]() ,
,![]() . Мінімуму такої функції знаходиться при виконанні умови виду:
. Мінімуму такої функції знаходиться при виконанні умови виду:
![]() (6.6)
(6.6)
Підставимо в (6.6) заміст функції ![]() - вираз
- вираз ![]() , та заміст
, та заміст ![]() з (6.4) підставимо поліном і визначимо частинні похідні в виразу (6.6) по кожному коефіцієнту
з (6.4) підставимо поліном і визначимо частинні похідні в виразу (6.6) по кожному коефіцієнту ![]() . В результаті отримуємо систему рівнянь виду:
. В результаті отримуємо систему рівнянь виду:
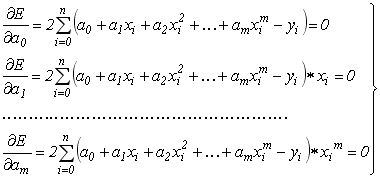
В даної системі розкриємо дужки та спростимо кожне рівняння системи окремо. В результаті отримаємо систему виду:
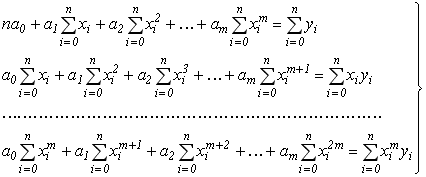 (6.7)
(6.7)
Система рівнянь (6.7) представляє собою систему лінійних алгебраїчних рівнянь відносно коефіцієнтів поліному ![]() , які необхідно знайти, щоб визначити аналітичну залежність, яка описує експериментальний масив даних. Дану систему можна записати у матричному вигляді:
, які необхідно знайти, щоб визначити аналітичну залежність, яка описує експериментальний масив даних. Дану систему можна записати у матричному вигляді:
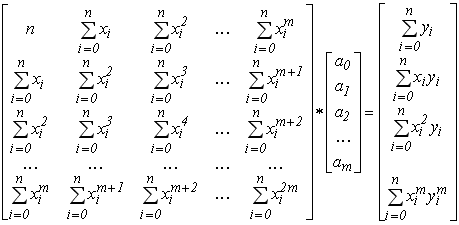
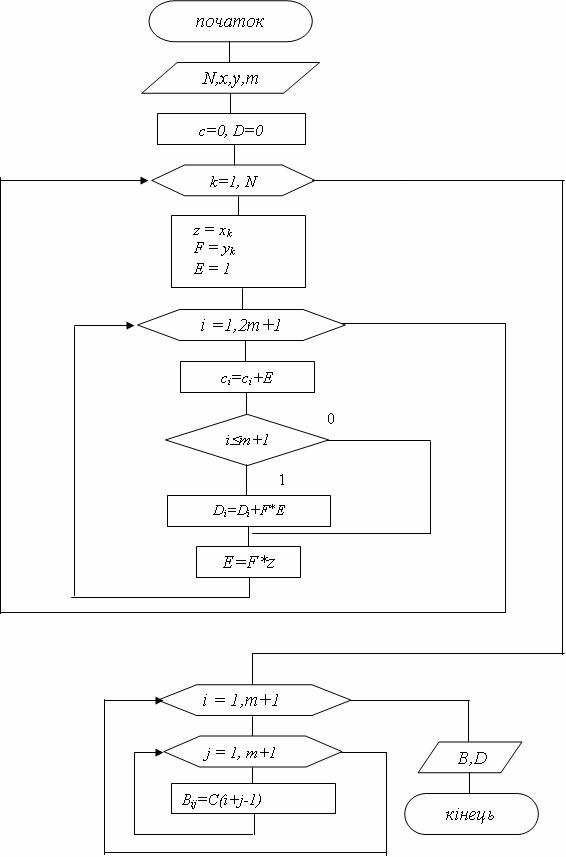
Для розв’язання такої системи на ЕОМ необхідно розробити спеціальний алгоритм та підпрограму для формування її матриці коефіцієнтів та вектора вільних членів з використанням експериментальних даних, які задані таблицею. На рисунку 6.2 представлений алгоритм формування системи лінійних алгебраїчних рівнянь (6.7) запропонований Делем В.Д. В ньому система (6.7) формується з метою зменшення кількості обчислювальних операцій (наприклад операції обчислення степеня), для цього введені допоміжні змінні та масиви ![]() і D. Зміна
і D. Зміна ![]() - містить поточне значення
- містить поточне значення ![]() ;
; ![]() - поточне значення
- поточне значення ![]() ;
; ![]() - множник, який багаторазово змінюється в процесі обчислення;
- множник, який багаторазово змінюється в процесі обчислення; ![]() - допоміжний масив із
- допоміжний масив із ![]() дійсних чисел, який являє собою суми
дійсних чисел, який являє собою суми ![]() (
(![]() ), що входять в кожне рівняння системи:
), що входять в кожне рівняння системи:
![]() ,
, 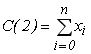 , ...,
, ..., 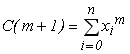 , ...,
, ..., 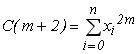
![]() - масив із
- масив із ![]() дійсних чисел, які являють собою суми вектора-стовпця вільних членів системи рівнянь (6.7) і визначають за допомогою допоміжних змінних
дійсних чисел, які являють собою суми вектора-стовпця вільних членів системи рівнянь (6.7) і визначають за допомогою допоміжних змінних ![]() та
та ![]() :
:
![]() ,
, ![]() ,
, ![]() ,
, ![]()
Розв‘язувати таку систему можна будь-яким з відомих методів розв‘язання системи лінійних алгебраїчних рівнянь, наприклад методом Гауса. Однак задача апроксимації на цьому етапі не завершується. Схема алгоритму побудови СЛАР методом Деля В.Д (6.7). представлена на рисунку 6.2.
Якщо для заданого степеня ![]() поліному
поліному ![]() в результаті розрахунків на ЕОМ отриманий поліном не відповідає заданої похибки обчислень
в результаті розрахунків на ЕОМ отриманий поліном не відповідає заданої похибки обчислень ![]() , то необхідно збільшити ступень поліному на 1 (тобто степінь полінома буде
, то необхідно збільшити ступень поліному на 1 (тобто степінь полінома буде ![]() ), при цьому на одиницю збільшується кількість коефіцієнтів поліному (додається новий член степеневого поліному), які необхідно знову розраховувати. При цьому розмір системи (6.7) збільшується на 1, і для визначення нових коефіцієнтів
), при цьому на одиницю збільшується кількість коефіцієнтів поліному (додається новий член степеневого поліному), які необхідно знову розраховувати. При цьому розмір системи (6.7) збільшується на 1, і для визначення нових коефіцієнтів ![]() необхідно знову розв’язувати систему (6.7) методом Гауса. Цей процес повторюється до тих пір, поки не виконається умова
необхідно знову розв’язувати систему (6.7) методом Гауса. Цей процес повторюється до тих пір, поки не виконається умова
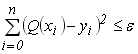 , (6.8)
, (6.8)
де ![]() - задана похибка отриманих результатів.
- задана похибка отриманих результатів.
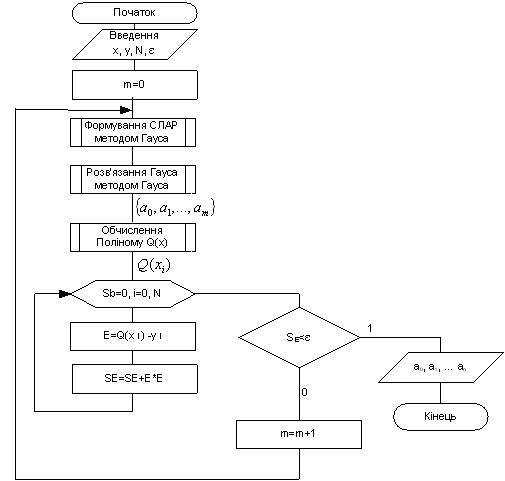
Схема алгоритму апроксимації функцій, заданих таблицею, методом найменших квадратів представлена на рисунку 6.3.
Постановка задачі
Припустимо, що в результаті інженерного або наукового експерименту отримана система точок: ![]() . Необхідно знайти аналітичну функцію виду:
. Необхідно знайти аналітичну функцію виду:
![]() , (6.9)
, (6.9)
таку що середне квадратичне відхилення цієї функції від заданої системи точок буде мінімальним:
![]() , (6.10)
, (6.10)
Розв’язання цієї задачі зводиться до знаходження коефіцієнтів аналітичної функції ![]() . Визначимо відхилення аналітичної функції
. Визначимо відхилення аналітичної функції ![]() від експериментальних даних в кожної i-ої точці
від експериментальних даних в кожної i-ої точці ![]() :
:
![]() (6.11)
(6.11)
З виразу (6.10) видно, що![]() залежит від коефіцієнтів
залежит від коефіцієнтів ![]() , тобто є функцією багатьох параметрів. З відомо, що умовою оптимуму багатопараметричної функції є умова виду:
, тобто є функцією багатьох параметрів. З відомо, що умовою оптимуму багатопараметричної функції є умова виду:
![]() (6.12)
(6.12)
підставимо в (6.12) заміст ![]() вираз(6.11) для всіх
вираз(6.11) для всіх ![]() і визначимо частинні похідні в виразу (6.12) по кожному коефіцієнту
і визначимо частинні похідні в виразу (6.12) по кожному коефіцієнту ![]() . В результаті отримуємо систему рівнянь виду:
. В результаті отримуємо систему рівнянь виду:
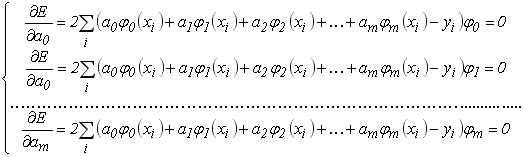 (6.13)
(6.13)
Після спрощення та рокриття дужек в кожному рівнянні система (6.13) буде мати вигляд:
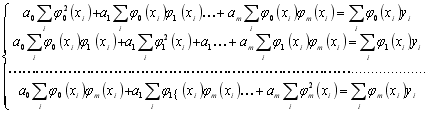 (6.14)
(6.14)
В матричній формі система (6.14) має вигляд:
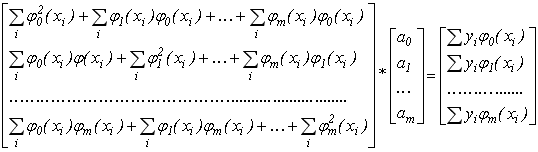 (6.15)
(6.15)
Вибір системи функцій ![]() здійснюється з врахуванням наявності в експериментальних даних деяких тенденций, наприклад, періодичність експериментальних даних, або експоненціальний або логарифмічний характер їх зміни, властивості симетрії або наявність асимптотики.
здійснюється з врахуванням наявності в експериментальних даних деяких тенденций, наприклад, періодичність експериментальних даних, або експоненціальний або логарифмічний характер їх зміни, властивості симетрії або наявність асимптотики.
Розглянемо спочатку поняття ортогональності та ортогональних функцій або системи функцій.
Функції ![]() і
і ![]() називаються ортогональними на заданій множині точок
називаються ортогональними на заданій множині точок ![]() , якщо сума попарних добутків цих функцій дорівнює 0.
, якщо сума попарних добутків цих функцій дорівнює 0.
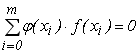 (6.16)
(6.16)
Система функцій ![]() називається ортогональною на заданій множині точок
називається ортогональною на заданій множині точок ![]() , якщо сума попарних добутків цих функцій дорівнює нулю, виключаючи добуток функції саму на себе.
, якщо сума попарних добутків цих функцій дорівнює нулю, виключаючи добуток функції саму на себе.
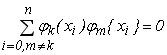 (6.17)
(6.17)
Величина ![]() =
=![]() називається нормою системи функцій
називається нормою системи функцій ![]() .
.
Якщо для заданої системи функцій ![]() на заданій множині точок
на заданій множині точок ![]() норма дорівнює одиниці, то така система функцій називається ортонормованою.
норма дорівнює одиниці, то така система функцій називається ортонормованою.
Якщо система функцій ![]() на заданій множині точок
на заданій множині точок ![]() ортогональна і норма системи функції більше 0, то така система функції називається лінійно незалежною.
ортогональна і норма системи функції більше 0, то така система функції називається лінійно незалежною.
Розглянемо математичні моделі апроксимації табличних функцій ортогональним поліномом.
Постановка задачі апроксимації
В результаті інженерного експерименту отримана система точок ![]() . Необхідно знайти аналітичну функцію вигляду
. Необхідно знайти аналітичну функцію вигляду
![]() , (6.18)
, (6.18)
яка найкращим чином описує задану систему точок і забезпечує суму квадратів відхилень аналітичної функції ![]() від експериментальної на заданій множині
від експериментальної на заданій множині ![]() . Тут
. Тут ![]() - задана система функций,
- задана система функций, ![]() - коефіціенти поліному.
- коефіціенти поліному.
Для розв’язування цієї задачі використовують метод найменших квадратів( МНК), який дозволяє звести задачу до двох:
- пошук коефіцієнтів апроксимуючої функції ![]() ;
;
- пошук оптимальної кількості ортогональних функції ![]() .
.
Для пошуку коефіцієнтів апроксимації використовують критерій СКВ:
![]()
за допомогою якого будують систему лінійних алгебраїчних рівнянь відносно невідомих коефіцієнтів ![]() виду:
виду:
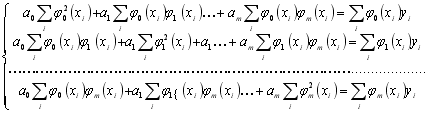 .(6.19)
.(6.19)
Якщо в якості системи функцій ![]() вибрати ортогональну систему функцій, то матриця коефіцієнтів перетворюється в діагональну матрицю, тобто в матрицю, в якої всі елементи дорівнюють 0, відповідно умові ортогональності (6.17), крім діагональних елементів ( для яких виконується умова
вибрати ортогональну систему функцій, то матриця коефіцієнтів перетворюється в діагональну матрицю, тобто в матрицю, в якої всі елементи дорівнюють 0, відповідно умові ортогональності (6.17), крім діагональних елементів ( для яких виконується умова ![]() . В цьому випадку в системі лінійних алгебраїчних рівнянь (6.19) кожне рівняння системи має тільки один невідомий коефіцієнт, тому для знаходження коефіцієнтів апроксимуючого поліному
. В цьому випадку в системі лінійних алгебраїчних рівнянь (6.19) кожне рівняння системи має тільки один невідомий коефіцієнт, тому для знаходження коефіцієнтів апроксимуючого поліному ![]() не треба розв’язувати системи лінійних алгебраїчних рівнянь а достатньо знайти їх за формулою:
не треба розв’язувати системи лінійних алгебраїчних рівнянь а достатньо знайти їх за формулою:
![]() . (6.20)
. (6.20)
Якщо умова ортогональності задовольняє умовам експерименту, то потрібно вибрати апроксимуючий ортогональний поліном або з таблиці 6.1 або з довідників спеціальних функций.
Пошук оптимальної кількості m функцій ![]() не потребує повторного обчислення коефіцієнтів поліному, тобто кожний новий коефіцієнт залежить тільки від заново вибраної функції
не потребує повторного обчислення коефіцієнтів поліному, тобто кожний новий коефіцієнт залежить тільки від заново вибраної функції ![]() . Ця властивість є перевагою метода апроксимації табличної функції ортогональними поліномами, тому що в методі апроксимації табличної функції степеневими поліномами при пошуку оптимального степеня поліному потрібно обчислення всіх коефіцієнтів
. Ця властивість є перевагою метода апроксимації табличної функції ортогональними поліномами, тому що в методі апроксимації табличної функції степеневими поліномами при пошуку оптимального степеня поліному потрібно обчислення всіх коефіцієнтів ![]() заново при кожному новому значенні m.
заново при кожному новому значенні m.
Висновок. В порівнянні з апроксимацією табличних функцій степеневими функціями - ортогональні поліноми спрощують задачу апроксимації, зменшують кількість обчислювальних операцій і дозволяють визначити коефіцієнти апроксимуючої функції без розв’язування СЛАР методом Гауса.
Рекурентні формули для обчислення найбільш поширених в обчислювальних методах ортогональних поліномів представлені в таблиці 6.1.
Таблиця 6.1 – Рекурентні формули для обчислення ортогональних поліномів
Поліном |
Формула |
Чебишева |
|
Ерміта |
|
Лежандра |
|
Ляггера |
|
В випадку коли за допомогою попереднього аналізу результатів інженерного або наукового експерименту функція, яка досліджується, має періодичний характер (рис. 6.4), то для апроксимації таких функцій звичайно використовують ортогональні поліноми Фур’є, які мають вигляд:
![]() (6.21)
(6.21)
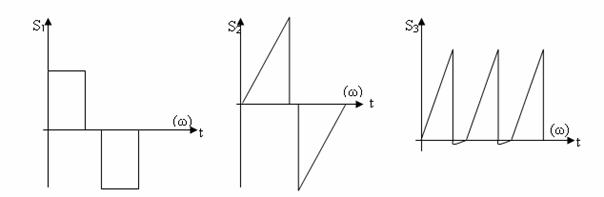
Багато задач науки і техніки зв'язані з періодичними функціями, які відображають циклічні процеси.
Функція f(x) називається періодичною з періодом T>0, якщо вона задовольняє рівності
![]() (6.22)
(6.22)
З практичних міркувань такі функції зручно подати в вигляді тригонометричного поліному або його часткової суми з заданої обчислювальною похибкою ![]() . Поліном виду:
. Поліном виду:
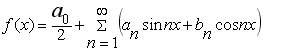 (6.23)
(6.23)
називається тригонометричним, причому an і bn - дійсні числа, які не залежать від x.
Нехай цей ряд збігається для будь-якого x з інтервалу ![]() , тоді він визначає періодичну функцію f(x) з періодом
, тоді він визначає періодичну функцію f(x) з періодом ![]() .
.
Рядом Фур'є називається ряд, коефіцієнти якого обчислюються за наступними формулами:
![]() , (6.24)
, (6.24)
та якщо функція f(x) неперервна на відрізку [-p,p].
Розглянемо особливості використання ряду Фур'є для інженерних задач. При цьому виникають наступні питання:
1) Чи збігається ряд Фур'є функції f(x) ?
2) Якщо ряд збігається, то чи буде він мати своєю сумою f(x)?
Відповіді на поставлені питання дає теорема Діріхлє. Перше ніж сформулювати саму теорему, нагадаємо деякі поняття. Функція f(x) називається монотонною на інтервалі, якщо для будь-яких x1 і x2, які належать цьому інтервалу і таких, що x1 < x2, виконується лише одна з нерівностей f(x1)Јf(x2) або f(x1)іf(x2). Функція f(x) називається кусково-монотонною на інтервалі, якщо його можна розбити на кінцеве число відкритих інтервалів, в кожному з яких функція монотонна.
![]() (6.25)
(6.25)
![]() (6.26)
(6.26)
Функція f(x) називається кусково-неперервною на інтервалі, якщо вона має на ньому кінцеве число точок розриву.
Позначимо через f(а + 0) границю функції f(x) коли х прямує до ![]() справа (права границя), відповідно, через f(а - 0) - ліва границя.
справа (права границя), відповідно, через f(а - 0) - ліва границя.
Теорема Діріхлє. Якщо функція f(x), яка задана в інтервалі [-p, p], кусково-монотонна і кусково-неперервна, то ряд Фур'є цієї функції збігається на всьому інтервалі [-p, p] і сума його дорівнює:
1. f(x) в усіх точках неперервності, які належать [-p, p];
2. ![]() [ f(x - 0) +f(x + 0)] в усіх точках розриву, які належать інтервалу [-p, p];
[ f(x - 0) +f(x + 0)] в усіх точках розриву, які належать інтервалу [-p, p];
Тобто
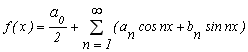
Теорема Діріхлє не стверджує рівномірної збіжності ряду Фур'є до функції f(x). Однак якщо посилити властивості, яким повинна задовольняти функція, тобто вимагати від неї неперервності на всьому інтервалі [-p, p], кускової монотонності на ньому і виконання рівності f(-![]() ) = f (
) = f (![]() ), то ряд Фур'є для такої функції буде рівномірно збігатися до функції f(x) на всьому інтервалі [-p, p].
), то ряд Фур'є для такої функції буде рівномірно збігатися до функції f(x) на всьому інтервалі [-p, p].
Можна показати, що для парної функції всі коефіцієнти bn дорівнюють нулю, а відповідний ряд Фур'є не містить синусів:
![]() , (6.27)
, (6.27)
де ![]() . (6.28)
. (6.28)
Аналогічно для непарної функції всі коефіцієнти аn дорівнюють нулю і відповідний ряд Фур'є не містить косинусів:
![]() ,
,![]()
![]() (6.29)
(6.29)
Де ![]() . (6.30)
. (6.30)
Чисельний гармонічний аналіз
Теоретичні та практичні засоби використання ряду Фур'є заміст функції f(x) в задачах моделювання і обробки результатів інженерних та наукових експериментів називається гармонічним аналізом. При практичних розрахунках необхідно обмежитися тільки декількома першими членами ряду Фур'є. В результаті можна отримати лише наближений аналітичний вираз для функції f(x) в вигляді тригонометричного багаточлену N-го порядку
![]() (6.31)
(6.31)
Крім того, формули (6.23), (6.24), (6.25) для обчислення коефіцієнтів Фур'є придатні лише в випадку аналітичного завдання функції. На практиці, як правило, функція f(x) задається в вигляді таблиць або графіків (рис. 6.4), тому виникає задача наближеного відшукування коефіцієнтів Фур'є. Узагальнюючи вищесказане, сформулюємо наступну задачу чисельного гармонічного аналізу: апроксимувати на інтервалі (0,Т) тригонометричним багаточленом m-го порядку функцію y= f(x), для якої відомі m її значень
![]() при xk =
при xk =![]() (к=0,1,2,..., m-1).
(к=0,1,2,..., m-1).
Тригонометричний багаточлен для функції, яка визначена на інтервалі (0,T), має вигляд
![]() , (0
, (0![]() x
x![]() T) (6.32)
T) (6.32)
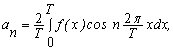 (6.33)
(6.33)
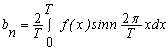 (6.34)
(6.34)
Використовуючи в співвідношеннях (6.31) і (6.32) формулу прямокутників для обчислення інтегралів за значеннями підінтегральних виразів в точках ![]() (k = 0,1,2,...,m -1), маємо
(k = 0,1,2,...,m -1), маємо
![]() (n=0,1,2,...,N) (6.35)
(n=0,1,2,...,N) (6.35)
![]() (6.36)
(6.36)
Таким чином, тригонометричний багаточлен (6.31), коефіцієнти an і bn, якого знаходяться за формулами (6.34) і (6.35), може бути використаний для розв’язання даної задачі.
1. Щуп Т. Решение инженерных задач на ЕВМ. – М.: Мир, 1982. – 235с.
2. Демидович Б. П., Марон И. А. Основы вычислительной математики. – М.: Наука, 1970. – 664 с.
3. Демидович Б. П., Марон И. А., Шувалова Е. З. Численные методы анализа. – М.: Мир, 1967
4. Мак – Кракен Д., Дрон У. Численные методы и програмирование на фортране. – М.: Мир, 1977. – 584 с.
5. Бахвалов Н. С. Численные методы . Т. И. Анализ, алгебра, обычные диференциальные уравнения. – М.: Наука, 1975. – 631 с.
6. Краскевич В. Є., Зеленський К. Х., Гречко В. И. Численные методы в инженерных исследованиях. – К.: Высшая шк.., 1986. – 263 с.
7. Рисс Ф., Секефальви – Надь Б. Лекции по функциональному анализу – М.: Мир, 1979.
8. Плис А.И., Сливина Н.А. Mathcad. Математический практикум для инженеров и экономистов: – М.: Финансы и статистика, 2003. – 656с.
9. Тихомиров В. М. Некоторые вопросы теории приближений. – М.: МГУ, 1976.
10. Ахиезер Н. И. Лекции по теории апроксимации. – М.: Наука, 1965.
11. В.И. Бердышев, Ю.Н. Субботин. Численные методы приближения функций. – Средне-Уральское книжное книжное издательство, 1979.
12. Суетин П. К. Классические ортогональные многочлены. – М.: Наука, 1976. – 327 с.
13. Альберг Дж., Нильсон Е., Уолт Дж. Теория сплайнов и ее дополнение. – М.: Мир, 1972.
14. Стечкин С. Б., Суботин Ю. Н. Сплайны в вычислительной математике. – М.: Наука, 1976.
15. Трауб Дж. Итерационные методы решения уравнений. – М.: Мир, 1985. – 263 с.
1. Загальна постановка задачі апроксимації.
2. Основні умови теореми Діріхлє.
3. Зробити постановку задачі на тригонометричну апроксимацію.
4. Суть методу найменших квадратів (МНК).
5. Вкажіть формули чисельного обчислення коефіцієнтів Фур’є.
6. Скласти алгоритм тригонометричної апроксимації.
7. Скласти схему алгоритму апроксимації степеневими поліномами.
8. Скласти схему алгоритму апроксимації ортогональними поліномами.
9. Розкласти в ряд Фур'є функцію f(x) = x sin( x) ![]() .
.
Відповідь: 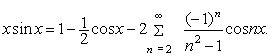
10. Загальна постановка задачі на інтерполяцію і апроксимацію
11. Що таке екстраполяція функції? Зробіть загальну постановку задачі.
12. Розкласти в ряд Фур'є функцію
![]()
Відповідь: