Так, наприклад, в результаті математичної обробки можна отримати наступну аналітичну залежність грошових кредитів в сільському господарстві під товарно-матеріальні цінності і сезонні витрати від витрат на велику рогату худобу: , де y - кредити під товарно-матеріальні цінності; - витрати на велику рогату худобу. Інший приклад аналітичної залежності: зв'язок шляху з часом в рівноприскореному русі виражається як .

Позитивною властивістю аналітичного способу завдання є можливість одержувати значення для будь-якого фіксованого аргументу з будь-якою точністю. До недоліків цього засобу слід віднести те, що потрібно повторювати всю послідовність обчислень; крім того, аналітичний засіб не володіє наочністю. Вказані недоліки аналітичного засобу усуваються у випадку графічного завдання функції .

Табличний спосіб завдання функцій розповсюджений у техніці, фізиці, економіці, природознавстві та найчастіше всього використовується для запису результатів експерименту.

Нехай, наприклад, в результаті досліду отримана залежність омічного опору R мідного стержня від температури у вигляді таблиці 5.1:

Таблиця 5.1 – Результати експериментальних досліджень

В цьому експерименті значення омічного опору мідного стержня змінюється при коливанні температури і є залежною змінною.

Перевагою табличного способу завдання експериментальної функції є те, що для кожного значення незалежної змінної, поміщеної в таблицю, можна відразу ж, без усяких вимірів і обчислень, знайти відповідне значення функції. Недолік табличного способу полягає в тому, що не можна задати всю функцію скрізь, тобто завжди знайдуться такі значення незалежної змінної, яких немає в таблиці. Тому, для аналізу результатів інженерних експериментів дуже зручно використовувати як табличний так і аналітичний способи представлення залежностей, що досліджуються.

Так, якщо в результаті інженерного або наукового експерименту отримана система точок: , то дуже часто виникає задача пошуку аналітичної залежності, яка б зв‘язувала експериментальні дані у вигляді аналітичної функції . Для розв’язування цієї задачі за допомогою чисельних методів на ЕОМ використовуються два підходи:

1. Інтерполяція – підхід, за допомогою якого отримують аналітичні залежності табличних функцій за умови, що аналітична функція повинна проходити через всі задані експериментальні точки.

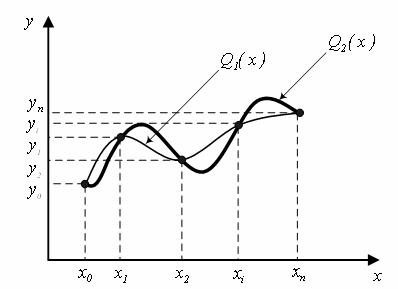
2. Апроксимація – підхід, за допомогою якого знаходиться аналітична функція , що “найкращим чином” наближається до заданої табличної функції. Звичайно “найкращим чином” – це критерій, в якості якого використовується критерій середньо квадратичного відхилення (СКВ), заснований на тому, що сума квадратів відхилень аналітичної функції від експериментальної (при і=0, 1, …, k) повинна бути мінімальною:

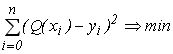
На рисунку 5.1 представлена класифікація відомих методів наближення табличних функцій, призначених для пошуку аналітичної залежності , яка б зв‘язувала експериментальні дані , отримані в результаті інженерного або наукового експерименту.

    

     5.2 Математична постановка задачі інтерполювання

В економіці і техніці постійно приходиться зіштовхуватися з необхідністю обчислення значень функції в точках , відмінних від значень аргументу, фіксованих в таблиці експериментальних досліджень. Крім того, в деяких випадках, незважаючи на те, що аналітичний вираз функції відомий, він є занадто складним і незручним для подальших математичних перетворень. Подібні задачі формалізуються як задачі інтерполювання.

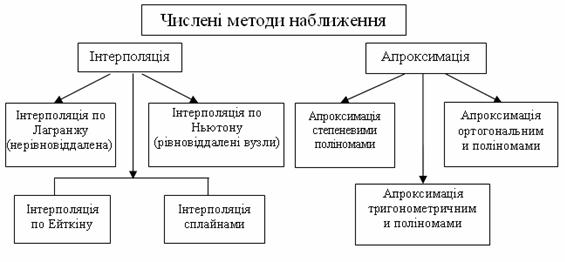
Нехай на відрізку функція задана системою точок , де значення називаються вузлами інтерполяції. Необхідно знайти аналітичну залежність , співпадаючої у вузлах інтерполяції зі значеннями заданої функції, тобто Процес обчислення значень функції в точках , відмінних від вузлів інтерполяції, називають інтерполюванням функції (рисунок 5.1).

Якщо аргумент знаходиться за межами відрізка інтерполювання , то задача визначення значення функції в точці називається екстраполюванням.

Слідує відмітити, що задача інтерполювання стає однозначною, якщо в якості функції вибрати багаточлен степені не вище n, такий, що . Багаточлен , що задовольняє цим умовам, називають інтерполяційним багаточленом, а відповідні формули – інтерполяційними формулами.

    

У випадку, коли береться з класу степеневих функцій, інтерполяція називається параболічною. Цей спосіб наближення ґрунтується на тому, що на невеликих відрізках експериментальна функція може бути достатньо добре апроксимована параболою певного порядку. Якщо в якості інтерполяційної функції використовувати багаточлен виду:

          (5.1)

то така інтерполяція називається степеневою

Інколи доцільно використати інші види інтерполяції. Якщо функція, що досліджується, – періодична, то в якості інтерполяційної функції () вибирають тригонометричну, наприклад, виду:

          (5.2)

і така інтерполяція називається тригонометричною. В деяких в якості інтерполяційної функції () вибирають раціональні функції.

При інтерполюванні виникає ряд задач:

1. вибір найбільш зручного способу побудови інтерполяційної функції для кожного конкретного випадку;

2. оцінка похибки при заміні інтерполяційною функцією на відрізку , оскільки функції та співпадають тільки у вузлах інтерполяції ;

3. оптимальний вибір вузлів інтерполяції для отримання мінімальної похибки.

Для задачі інтерполювання важливим є визначення того, як повинна вести себе інтерполяційна функція між заданими точками, так як ці точки можуть бути інтерпольовані множиною різноманітних функцій, і необхідно мати певний критерій вибору. Звичайно критерій формується в термінах гладкості та простоти. Більшість інтерполяційних функції генеруються лінійними комбінаціями найпростіших функцій. Лінійні комбінації одночленів формують степеневі поліноми, лінійні комбінації тригонометричних функцій формують тригонометричні поліноми, використовуються також лінійні комбінації експонент . Найбільш важливим класом інтерполяційних функцій є множина алгебраїчних поліномів. Поліноми мають переваги з точки зору алгоритмізації, тому що їх значення легко обчисляти, додавати, перемножувати, інтегрувати чи диференціювати. Важливою властивістю поліномів є те що якщо с – константа, а p(x)- поліном, то поліномами будуть і p(cx) і p(x+c)

Клас інтерполяційних функції обирають, використовуючи теорему Вейерштраса:

Якщо f(х) – неперервна на кінцевому інтервалі функція, то для любого існують поліном p_n(x) ступеня n такий, що .

     5.2.1 Інтерполяційний багаточлен Лагранжа

Найбільш загальною формулою параболічного інтерполювання є інтерполяційна формула Лагранжа. Задача параболічного інтерполювання в цьому випадку формулюється наступним чином: на відрізку у вузлах інтерполяції задається функція своїми значеннями

,

необхідно побудувати багаточлен так, щоб у вузлах інтерполяції його значення співпадали зі значеннями заданої функції, тобто …, Слід відзначити, що в такій постановці задачі вузли інтерполяції можуть бути довільно розташовані один від одного на відрізку , іншими словами, вузли інтерполяції не рівновіддалені, тобто . Величина називається кроком інтерполяції.

Задача інтерполювання має розв‘язок, якщо степінь m багаточлена яким замінюється функція , не вище порядку (). Тоді задача інтерполювання зводиться до пошуку невідомих постійних коефіцієнтів багаточлена з системи рівнянь, яка будується наступним чином. З початкових умов відомо, що функція в вузлах приймає значення Тоді в вузлі інтерполяційний

багаточлен має вигляд в вузлі інтерполяції - і так далі. Нарешті, в вузлі інтерполяційний багаточлен буде виглядати

.

Запишемо це у вигляді системи рівнянь з невідомими

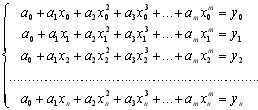     ,     (5.3)

де і табличні значення аргументу і функції, що досліджується. Невідомі коефіцієнти знаходяться по формулам Крамера:

     ,     (5.4)

де - визначник системи (5.3).

Якщо (тобто коли різні), то система (5.3) має єдиний розв’язок. Якщо знайти коефіцієнти , можна уявити інтерполяційний багаточлен у вигляді

Перепишемо багаточлен в іншій формі:

               (5.5)

Легко перевірити, що функція повинна задовольняти умовам

          (5.6)

В точках функція обертається в 0, а в точці дорівнює 1.

Остаточно отримаємо вираз (5.7)

          (5.7)

Цей багаточлен називається інтерполяційним багаточленом Лагранжа. В спрощеному вигляді його можна записати так:

          (5.8)

Даний метод легко алгоритмізується і може використовуватися для розробки програм інтерполяції. Схема алгоритму метода представлена на рисунку 5.3.

    

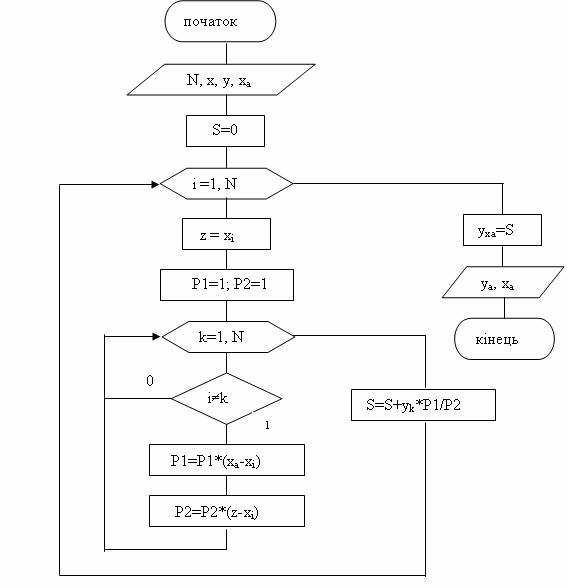
Приклад: Побудувати інтерполяційний багаточлен Лагранжа для функції заданої таблично.

n=4; m=n-1=4-1=3. Припустимо, що y=a₀+a₁x+a₂x²+a₃x^3.

Слід пам’ятати, що при екстраполяції функції, чим далі значення х від інтервалу спостереження, тим отримане значення функції містить більшу похибку.

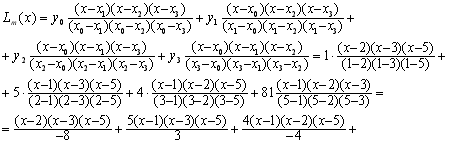
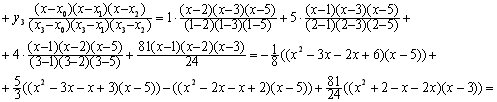
Таким чином: , , , .

Висновки:

1. Таким чином за допомогою багаточлена Лагранжа були отримані коефіцієнти інтерполяційної функції : .

2. Використовуючи отриманий багаточлен можливо знайти будь-яке значення функції для заданого . Наприклад, для

3. Використовуючи інтерполяційний багаточлен можливо отримати значення функції за межами спостережень. У даному прикладі інтервал спостереження . Така задача називається екстраполяція (прогнозування функції).

Для оцінки похибки інтерполяційного багаточлена Лагранжа використовують формулу:

,

причому , при

     5.2.2 Перша інтерполяційна формула Ньютона для рівновіддалених вузлів інтерполяції

Якщо функція, що досліджується, задана значеннями в рівновіддалених вузлах інтерполяції, тобто , то для побудови її аналітичної залежності зручно використовувати першу інтерполяційну формулу Ньютона.

Для виводу інтерполяційних формул для рівновіддалених вузлів інтерполяції вводиться поняття кінцевої різниці.

Поставимо наступну задачу: для функції , яка задана таблицею значень причому x змінюється з однаковим кроком h, тобто , побудувати кінцеві різниці.

Кінцевою різницею першого порядку називається різність між значеннями функції в сусідніх вузлах інтерполяції:

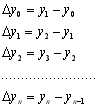
В загальному вигляді кінцеву різницю першого порядку можна записати як .

Кінцева різниця другого порядку складається з кінцевих різниць першого порядку:

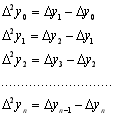
Кінцева різниця n-го порядку складається з кінцевих різниць -го порядку:

,

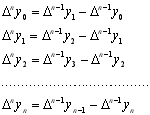або в технічної літературі використовують наступну формулу кінцевої різниці -го порядку:

Нехай необхідно побудувати інтерполяційний багаточлен степеню такий, що

     Будемо шукати багаточлен виду (5.9)

В цьому виразі невідомі коефіцієнти . Для того щоб знайти , покладемо . Тоді при підстановці в вираз (5.9) всі складові, окрім першої, обернуться в нуль, тобто а значення функції в точці відомі з умови задачі: Отже

Щоб знайти коефіцієнт складемо першу кінцеву різницю для багаточлена в точці x:

Зробивши всі підстановки, отримаємо:

Обчислимо першу кінцеву різницю багаточлена в точці Тут також всі члени, окрім першого, обернуться в нуль, і, отже, але

звідки і

Щоб визначити коефіцієнт складаємо кінцеву різницю другого порядку:

Після перетворень отримаємо

Вважаємо ; тоді всі члени, окрім першого, знов обернуться в нуль і Звідси

Обчислюючи кінцеві різниці більш високих порядків і вважаючи , прийдемо до загальної формули для отримання коефіцієнтів:

          (5.10)

де будемо вважати, що та Підставивши знайденні значення коефіцієнтів в вираз (5.9), отримаємо першу інтерполяційну формулу Ньютона.

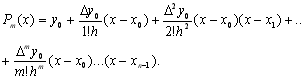          (5.11)

На практиці часто використовують формулу Ньютона в іншому вигляді. Для цього введемо заміну де крок інтерполяції, а q - число кроків. Тоді перша інтерполяційна формула Ньютона прийме наступний вигляд:

     (5.12)

Формулу (5.12) зручно використати для інтерполювання на початку відрізку інтерполяції , де q мале за абсолютною величиною.

Якщо за число вузлів інтерполяції прийняти , то отримаємо формулу лінійного інтерполювання

При отримаємо формулу параболічного, або квадратичного інтерполювання

На практиці часто буває необхідно зменшити крок інтерполяції якої-небудь таблиці з рівновіддаленими аргументами. В таблиці можна вважати, що кількість вузлів інтерполяції необмежена. Тоді вибирають так, щоб кінцева різниця була постійна з заданим ступенем точності. За початкове значення можна вибирати будь-яке значення аргументу.

Схема алгоритму інтерполяції табличної функції багаточленом Ньютона представлена на рисунку 5.4.

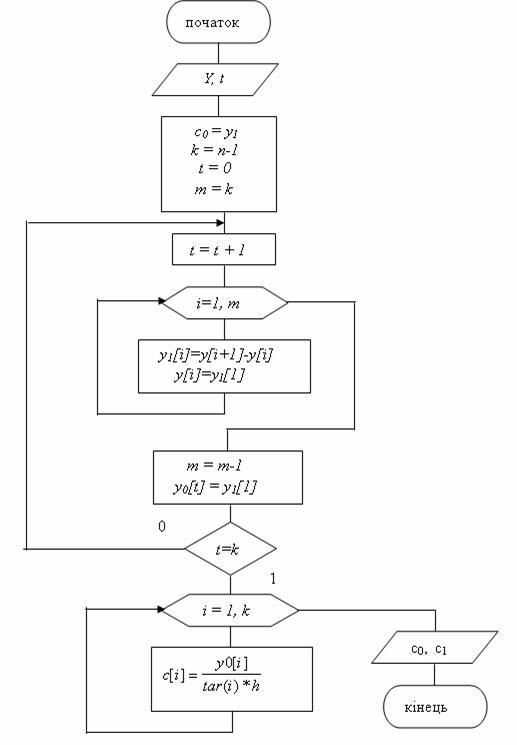
Рисунок 5.4 – Схема алгоритму інтерполяції табличної функції багаточленом Ньютона

Приклад. Припустимо, що результати експерименту представлені в таблиці 5.2 (перших три стовпця)

З таблиці видно, що

,

Таблиця 5.2 – Результати експерименту

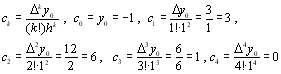
Побудуємо багаточлен Ньютона:

Q=-1+3x+6(x(x-1))+1(x(x-1)(x-2))+0=-1+3x+6x2-6x+x3-2x2-x2+2x=x3+3x2-x-1

Висновки:

1. За допомогою аналітичної залежності можливо отримати значення функції для , які знаходяться між точками дослідження. отримуємо це називається задачею інтерполяції.

2. За допомогою аналітичної залежності можна отримати значення функції за межами інтервалу дослідження. Наприклад, при . Дана задача називається екстраполяцією або прогнозуванням.

     Література

1. Щуп Т. Решение инженерных задач на ЕВМ. – М.: Мир, 1982. – 235с.

2. Демидович Б. П., Марон И. А. Основы вычислительной математики. – М.: Наука, 1970. – 664 с.

3. Демидович Б. П., Марон И. А., Шувалова Е. З. Численные методы анализа. – М.: Мир, 1967

4. Мак – Кракен Д., Дрон У. Численные методы и програмирование на фортране. – М.: Мир, 1977. – 584 с.

5. Бахвалов Н. С. Численные методы . Т. И. Анализ, алгебра, обычные диференциальные уравнения. – М.: Наука, 1975. – 631 с.

6. Краскевич В. Є., Зеленський К. Х., Гречко В. И. Численные методы в инженерных исследованиях. – К.: Высшая шк.., 1986. – 263 с.

7. Рисс Ф., Секефальви – Надь Б. Лекции по функциональному анализу – М.: Мир, 1979.

8. Плис А.И., Сливина Н.А. Mathcad. Математический практикум для инженеров и экономистов: – М.: Финансы и статистика, 2003. – 656с.

9. Тихомиров В. М. Некоторые вопросы теории приближений. – М.: МГУ, 1976.

10. Ахиезер Н. И. Лекции по теории апроксимации. – М.: Наука, 1965.

11. В.И. Бердышев, Ю.Н. Субботин. Численные методы приближения функций. – Средне-Уральское книжное книжное издательство, 1979.

12. Суетин П. К. Классические ортогональные многочлены. – М.: Наука, 1976. – 327 с.

13. Альберг Дж., Нильсон Е., Уолт Дж. Теория сплайнов и ее дополнение. – М.: Мир, 1972.

14. Стечкин С. Б., Суботин Ю. Н. Сплайны в вычислительной математике. – М.: Наука, 1976.

15. Трауб Дж. Итерационные методы решения уравнений. – М.: Мир, 1985. – 263 с.

     Питання та задачі до самостійної роботи

1. Загальна постановка задачі інтерполяції.

2. Що називається інтерполяційним багаточленом, вузлами інтерполяції?

3. Для функції y = f(x), яка визначена на інтервалі (0, ) і задана в вигляді таблиці значень y_k = f(x_k):

скласти тригонометричний інтерполяційний багаточлен.

Відповідь:

4. Для функції y = f(x), яка визначена на інтервалі (0, 1) і задана у вигляді таблиці значень y_k = f(x_k):

скласти тригонометричний багаточлен не нижче другого порядку.

Відповідь:

5. Побудувати інтерполяційний багаточлен Лагранжа для функції, яка задана таблицею

Відповідь:

6. Побудувати багаточлен Ньютона для функції, заданої таблицею:

7. Зробити постановку задачі на інтерполяцію функції, яка задана таблицею з не рівновіддаленими вузлами інтерполяції.

8. Зробити постановку задачі на інтерполяцію функції, яка задана таблицею з рівновіддаленими вузлами інтерполяції.~

< Зміст >